2. 中国石油天然气股份有限公司 冀东油田分公司, 唐山 063004
2. Jidong Oilfield Branch, Petro China Co. Ltd., Tangshan 063004, China
随着互联网技术的快速发展, 图像, 文本, 视频, 音频, 三维模型等多媒体数据量越来越多, 多媒体信息检索[1]发展迅速, 其中跨媒体检索是研究热点. 跨媒体检索[2]是指任意使用一种媒体数据对其他媒体数据在语义层面进行相关性检索, 实现多媒体数据在语义上的互通. 其难点在于, 不同媒体类型的数据表示形式不一致, 导致它们之间存在异构性. 而且, 不同媒体类型的数据特征维度高, 导致检索效率低是具有挑战性的问题. 针对此问题, 哈希学习将不同媒体数据从高维表示空间映射到低维汉明空间, 同时将原始数据的相关性尽可能保留到汉明空间, 使在同一语义下的不同媒体数据具有相似的哈希码. 因此, 哈希学习成为研究跨媒体检索的一类代表性方法.
目前主流的跨媒体哈希检索方法主要分为两类:一类是无监督跨媒体哈希方法和有监督跨媒体哈希方法. 其无监督跨媒体哈希是指不使用语义标签信息进行学习, 而是通过捕捉底层数据的结构, 分布以及拓扑信息来学习哈希函数. 例如媒体间哈希(Inter-Media Hashing, IMH)[3], 协同矩阵分解哈希(Collective MatrixFactorization Hashing, CMFH)[4], 跨媒体相似检索的潜在语义稀疏哈希(Latent Semantic Sparse Hashing for cross modal similarity search , LSSH)[5]等方法. 有监督跨媒体哈希方法主要利用语义标签信息的指导学习哈希函数. 如跨视角哈希(Cross View Hashing, CVH)[6], 最大语义关联跨媒体检索(Semantic Correlation Maximization, SCM)[7], 语义保留哈希跨媒体检索(Semantics Preserving Hashing, SePH)[8]等方法, 而以上这些方法尽管利用语义标签信息减轻了不同媒体类型数据之间的异构差距, 但是在哈希函数学习的过程中没有使用深层次的特征表示. 深度学习利用神经网络强化媒体之间相关性学习, 可以大幅度提升检索效果. 深度视觉语义哈希(Deep Visual-Semantics Hashing, DVSH)[9], 通过利用CNN和LSTM分别提取图像表示和文本表示, 为图像和文本数据分别学习哈希函数, 同时保留了模态内和模态间的相关性. 深度跨模态哈希(Deep Hashing Cross Modal Retrieval, DCMH)[10]是这类方法的一个代表, 它是一个端到端的框架, 将图像和文本的特征学习与哈希学习统一起来, 将不同模态间的相关性保留到哈希码, 实现比较好的效果. 再如, 基于三元组的跨模态深度哈希方法[11], 利用Triplet损失函数学习图像和文本之间的相似性, 增强对模态间相关性的学习.
综上所述, 为了使得语义相似的媒体对象哈希码的距离较小, 语义不相似的媒体对象哈希码的距离较大, 使得汉明空间和语义空间具备结构性保持, 进而提高模型的检索效果, 本文提出基于柯西分布的深度哈希跨媒体检索方法, 该方法使用基于柯西函数的损失函数, 减小同类别下哈希码之间距离的同时, 增加不同类别间哈希码的距离, 从而提高模型的检索效果.
1 本文方法本文方法的整体框架示意如图1所示, 通过神经网络为不同媒体类型的数据学习哈希函数, 再利用哈希函数将不同媒体类型的数据映射到一个公共的汉明空间, 得到统一的哈希码. 在公共的汉明空间内, 不同于现有的基于交叉熵的关联损失函数, 本文引入基于柯西分布的跨媒体损失函数, 它不但能够缩小语义相似媒体对象的哈希码之间的距离, 而且可以增大语义不相似的媒体对象的哈希码距离, 从而提高跨媒体检索效果.

|
图 1 整个算法的流程示意图 |
1.1 形式化描述
本文以图像和文本为例进行介绍, 令
本文的主要任务是为不同媒体类型的数据学习哈希函数. 设
本文的网络框架主要分为两部分, 一部分用于提取图像特征, 另一部分用于提取文本特征.
对于图像数据, 我们对ResNet-34[12]做了一些改变, 网络配置如表1所示, 总共有10层, 其中前8层为卷积层, 第9为全连接层, 第10层是将图像特征映射到汉明空间, 而在第10层的特征维度应该与哈希码的长度一致, 每个卷积层内参数的含义如表1所示.
| 表 1 图像神经网络配置 |
“kernel num*size*size”描述了关于卷积核的信息, “num”表示输出通道数, size*size表示卷积核的大小.
“stride size*size”描述了关于卷积操作的步长, “stride”表示步长大小
“BN[13]”表示对网络层进行归一化
“max_pool:size*size”描述了下采样的大小,
“avg_pool:size*size”描述了下采样的大小.
每一个全连接层的数字. 例如“4096”表示这个全连接层的输出维度, k表示哈希码长度.
对于一个图像样本xi, 本文方法获得哈希码
对于文本数据, 我们使用词袋模型对文本数据进行预处理, 再输入两层玻尔兹曼机获得句子的深度特征表示, 文本神经网络配置如表2所示, 前两层的激活函数使用ReLU, 最后一层使用tanh函数, 同时特征长度与哈希码的长度保持一致.
| 表 2 文本神经网路配置 |
对于每一个文本yj, 本文方法获得的哈希码
令
| $\begin{split} p\left( {{s_{ij}}|\left( {h_i^x,h_j^y} \right)} \right) =& \left\{ {\begin{array}{*{20}{l}} {\sigma ({\varphi _{ij}})},&{{s_{ij}} = 1}\\ {1 - \sigma ({\varphi _{ij}}),}&{{s_{ij}} = 0} \end{array}} \right.\\ = &\sigma {({\varphi _{ij}})^{{s_{ij}}}}{(1 - \sigma({\varphi _{ij}}))^{{s_{ij}}}} \end{split} $ | (1) |
其中,
| $ \begin{split} L &= - \log p\left( {S|\left( {{h^x}, {h^y}} \right)} \right)\\ &{{ = }}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\log p\left( {{s_{ij}}|h_i^x, h_j^y} \right)} }\\ &= - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{s_{ij}}\log } } \sigma ({\varphi _{ij}}) + (1 - {s_{ij}})\log (1 - \sigma ({\varphi _{ij}})) \end{split} $ | (2) |
根据式(1), 式(2), 若
目前方法大多数使用Sigmoid函数作为式(2)的实现, Sigmoid函数的定义如下:
| $\sigma({\varphi _{ij}}) = \frac{1}{{1 + {{\rm e}^{ - {\varphi _{ij}}}}}}$ | (3) |
将哈希码之间的汉明距离
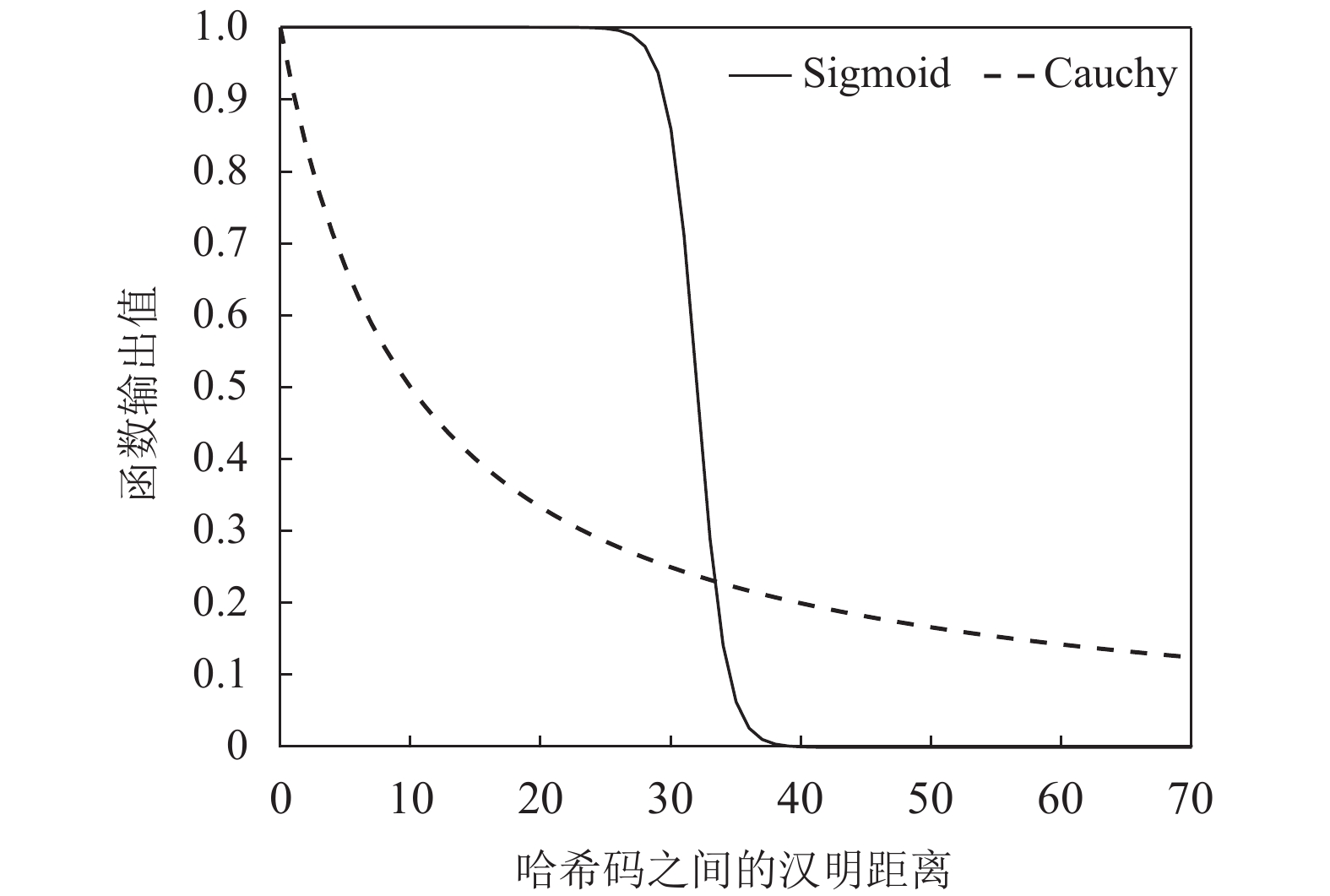
|
图 2 Sigmoid函数与Cauchy分布的输出随汉明距离
|
如图2所示, 采用Sigmoid函数, 当两个媒体对象的汉明距离较小时, 其相似度区分能力很弱. 但是如果采用柯西(Caughy)分布作为式(2)中
| $\sigma ({\varphi _{ij}}){\rm{ = }}\frac{\gamma }{{\gamma {\rm{ + }}{\varphi _{ij}}}}$ | (4) |
其中,
综上所述, 将式(4)带入式(2)并化简后, 可得改进后得损失函数:
| $ \begin{split} {L_{cau}} = & - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{s_{ij}}\log \left( {dist\left( {h_i^x, h_j^y} \right)/\gamma } \right)} } \\ &+ {\log \left( {1 + \gamma /dist\left( {h_i^x, h_j^y} \right)} \right)} \end{split}$ | (5) |
根据1.2节可知, 由于图像和文本神经网络输出层使用tanh函数, 图像和文本特征向量的取值范围是[−1, 1], 所以哈希码存在量化误差, 使用跨媒体哈希码, 需要学习哈希函数, 则哈希码量化损失表示为式(6):
| $ \begin{split}{L_q} =& \alpha \left( {\left\| {{{{h}}^x} - {\mathbf{B}}} \right\|_F^2 + \left\| {{{{h}}^y} - {\mathbf{B}}} \right\|_F^2} \right)\\ &{\rm{ }}\begin{array}{*{20}{c}} {{\rm{s}}{\rm{. t}}{\rm{. }}}&{{\mathbf{B}} \in {{\{ - 1, 1\} }^{k \times n}}} \end{array}\end{split}$ | (6) |
其中,
结合式(4), 式(6), 得到本文方法的目标函数为:
| $ \begin{split} &\mathop {\min}\limits_{{\mathbf B}, {\theta _x}, {\theta _y}} L = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{s_{ij}}\log \left( {dist\left( {h_i^x, h_j^y} \right)/\gamma } \right)} } \\ & +\log \left( {1 + \gamma /dist\left( {h_i^x, h_j^y} \right)} \right) + \alpha \left( {\left\| {{{{h}}_x} - {\mathbf{B}}} \right\|_F^2 + \left\| {{{{h}}_y} - {\mathbf{B}}} \right\|_F^2} \right)\\ &\begin{array}{*{20}{c}} {{\rm{s}}{\rm{. t}}{\rm{. }}}&{{\mathbf{B}} \in {{\{ - 1, 1\} }^{k \times n}}} \end{array}\end{split}\!\!\!\!\!\!\!\!\!\!\!\!$ | (7) |
由于目标函数是一个非凸问题, 若在求解一个变量的同时固定其他变量, 此时目标函数就变成凸优化问题, 可以使用梯度求导解决此问题, 因此本文采用一种交替迭代求解的策略获得目标函数的近似最优解, 具体的求解过程如下所示.
(1)更新
| $ \begin{split} \frac{{\partial L}}{{\partial h_i^x}} =& \sum\limits_{i,j = 1}^n {{s_{ij}}\left( {\frac{\gamma }{{dist\left( {h_i^x,h_j^y} \right)}} + \frac{{dist\left( {h_i^x,h_j^y} \right)}}{{\gamma + dist\left( {h_i^x,h_j^y} \right)}}} \right)} \\ &+{2\alpha \left( {b - h_i^x} \right)} \end{split}$ | (8) |
同时, 利用反向传播算法计算
(2)更新
| $ \begin{split} \frac{{\partial L}}{{\partial h_i^y}} =& \sum\limits_{i,j = 1}^n {{s_{ij}}\left( {\frac{\gamma }{{dist\left( {h_i^x,h_j^y} \right)}} + \frac{{dist\left( {h_i^x,h_j^y} \right)}}{{\gamma + dist\left( {h_i^x,h_j^y} \right)}}} \right)} \\ &+{2\alpha \left( {b - h_i^y} \right)} \end{split} $ | (9) |
同时, 利用反向传播算法计算
(3)更新B, 固定
| $\begin{split} \mathop {\min }\limits_{\mathbf{B}} L =& \alpha \left( {\left\| {{{\mathbf{h}}^x} - {\mathbf{B}}} \right\|_F^2 + \left\| {{{\mathbf{h}}^y} - {\mathbf{B}}} \right\|_F^2} \right)\\ &\begin{array}{*{20}{c}} {{\rm{s}}{\rm{. t}}{\rm{. }}}&{{\mathbf{B}} \in {{\{ - 1, 1\} }^{k \times n}}} \end{array}\end{split}$ | (10) |
对式(10)进行进一步整理可得如下公式:
| $ \begin{array}{l} \mathop {\min }\limits_{\mathbf{B}} L = \alpha \left( 2{{\mathbf{B}}^{\rm{T}}}{\mathbf{B}} - 2{\left( {{{\mathbf{h}}^x} + {{\mathbf{h}}^y}} \right)^{\rm{T}}}{\mathbf{B}} + {\left( {{{\mathbf{h}}^x}} \right)^{\rm{T}}}{{\mathbf{h}}^x} +{\left( {{h}^{{y}}} \right)}^{\rm T}{h}^{{y}} \right)\end{array}$ | (11) |
显然, 在上述公式中
| ${\bf{B}} = {\rm{sgn}}\pi \left( {\alpha \left( {{{\bf{h}}^x} + {{\bf{h}}^y}} \right)} \right) $ | (12) |
迭代该算法, 直到满足收敛准则.
1.6 外样本扩展对于那些不在训练集的样本点, 首先将它们转化为哈希码. 特别地, 给一个图像的样本查询点
| $b_q^x{\rm{ = }}{{{g}}^x}({x_q}) = \operatorname{sgn} (f({x_q}, {\theta _x}))$ | (13) |
同理, 对于一个文本的样本查询点
| $b_q^{{y}}{\rm{ = }}{{{g}}^y}({y_q}) = \operatorname{sgn} (f({y_q}, {\theta _y}))$ | (14) |
如1.1节所述, 本文方法只是以图文互相检索为例, 事实上, 本文可以扩展为任意两个媒体进行检索, 主要区别在于获取特征的方法.
2 实验结果与分析本文的基于柯西分布的深度哈希 跨媒体检索方法在Flickr-25k[14], IAPR TC-12[15], MS_COCO[16]三个标准数据集上进行试验, 并与最大语义关联哈希(SCM)[7], 深度跨模态哈希方法(DCMH)[10], 在图像检索文本, 文本检索图像两个任务进行了性能分析.
2.1 数据集Flickr-25k数据集共包含25015张图像组成, 每张图像都有几个文本标记相关联, 每张图片大概有标记8个或者9个, 数据集总共24个类别标签, 都是由人工标注的. 本文选组标记单词出现次数高于20的样本作为实验数据, 最终实验数据为20015个图像文本对.
IAPR TC-12数据集共包含20000张图像以及相对应的文本句子, 总共275个类别标签, 通过对数据集预处理之后, 去除没有类别标签的数据, 实验数据总共挑选19998个图像文本对.
MS COCO数据集共包含82785张训练集图像和40504张验证集图像, 同时每张图像都有5条描述的句子, 80个类别标签, 在本次实验中, 去掉没有类别标签和没有文本的描述的图像, 同时选取最能描述图像的句子作为文本数据, 最终实验数据有122218个图像文本对.
2.2 实验环境的设置及评价指标本文的实验在深度学习框架PyTorch上进行, 对于图像, 使用ImageNet[17]的预训练模型初始化图像特征提取网络ResNet-34, 并对输出层网络参数进行随机初始化, 对于文本, 使用词袋模型对文本数据进行预处理, 然后输入到多层玻尔兹曼机中, 获得其深度特征表示.
本文使用Rmscrop对训练网络模型, 学习参数配置如下: 图像网络的初始化学习率为0. 0001, 文本网络的初始化学习率0. 0003, 学习率每训练15次迭代后学习率变为当前值的1/2, 式(7)中参数
使用平均精度均值(Mean Average Precision, MAP)评价模型, 具体地, 存在一个查询样本q及其返回结果的列表, 平均准确率(Average Precision, AP)的定义为:
| $AP(q) = \frac{1}{{{N_q}}}\sum\limits_{m = 1}^{{n_q}} {P(m)I(m)} $ | (15) |
其中,
本文方法与其他基准模型在Flickr-25k, IAPR TC-12, MSCOCO数据集上MAP的结果如表3所示. 本次实验主要有两个任务: (1) Text-Image: 表示为图像检索文本, (2) Image-Text: 表示为文本检索图像与当前最好的模型DCMH[10]相比, 在Flickr-25k数据集上的图像检索文本的任务, 本文方法在哈希码为16位时提高了2.02%, 32位时提高了2.11%, 64位时提高了1.57%; 同时在文本检索图像时, 本文方法在哈希码16位时提高了3.01%, 32位时提高了2.98%, 64位时提高了3.41%; 在IAPR TC-12数据集上的文本检索图像时, 本文方法在哈希码为16位时提高了3.45%, 在32位时3.88%, 在64位时提高了5.32%, 同时在图像检索文本的任务, 本文方法在哈希码为16位时提高了12.61%, 32位时提高了10.29%, 64位时提高了13.45%; 在MSCOCO数据集上的文本检索图像时, 本文方法在哈希吗16位时提高了8.68%, 32位时提高了7.71%, 64位时提高了8.53%, 同时在图像检索文本任务, 本文方法在哈希码为16位时提高了6.80%, 32位时提高了4.31%, 64位时提高了5.47%. 以上的数据表明了本文方法可以学习到更有判别能力的哈希码.
| 表 3 在Flickr-25k, IAPR TC-12, MSCOCO数据集上的MAP值 |
本文方法与DCMH[10]都是以监督式的深度学习为基础的. DCMH方法是基于交叉熵的关联损失函数, 使用Sigmoid函数表示不同媒体对象哈希码的语义相似度, 只有汉明距离在k/2周围时, 不同媒体对象哈希码的语义相似度才具有判别力, 而本文方法通过引入柯西分布提出基于柯西分布的关联损失函数, 使不同媒体对象哈希码的距离更小, 获取更具有判别力的语义相似度, 进而提升跨媒体哈希检索效果.
2.4 Caughy参数对性能的影响为了够验证Caughy参数

|
图 3 不同的汉明距离在不同
|
另外, 本文在表4和表5分别展示了本文方法的文本检索图像和图像检索文本两个任务在Flickr-25k数据集上的一些例子. 在表4和表5中, 最左边的一列代表查询样本的标签, 中间列代表查询样本, 最右边的一列代表检索结果, 哈希码的长度为64 bit. 表4展示文本检索图像的例子, 中间列为图像, 最右边列为图像检索文本的结果, 该结果通过计算查询图像的哈希码与被检索文本哈希码之间的汉明距离, 再按照汉明距离从小到大按顺序排列, 获得与查询图像最相似的文本. 同理. 表5展示图像检索像的例子, 中间列为文本, 最右边列为文本检索图像的结果.
3 结论本文提出了一种基于柯西分布的深度哈希跨媒体检索模型, 它能够产生质量较高哈希码. 通过在Flickr-25k, IAPR TC-12和MSCOCO三个数据集上与现有方法的对比, 证明本文方法在跨媒体图文检索任务上的有效性. 但本文方法只是图文之间的检索, 下一步工作将他们应用到其他媒体类型数据, 例如图像与视频相互检索, 文本与视频相互检索.
| 表 4 文本检索图像的例子 |
| 表 5 图像检索文本的例子 |
| [1] |
庄毅, 庄越挺, 吴飞. 一种支持海量跨媒体检索的集成索引结构. 软件学报, 2008, 19(10): 2667-2680. |
| [2] |
卓昀侃, 綦金玮, 彭宇新. 跨媒体深层细粒度关联学习方法. 软件学报, 2019, 30(4): 884-895. DOI:10.13328/j.cnki.jos.005664 |
| [3] |
Song JK, Yang Y, Yang Y, et al. Inter-media hashing for large-scale retrieval from heterogeneous data sources. Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York, NY, USA. 2013. 785–796.
|
| [4] |
Ding GG, Guo YC, Zhou JL. Collective matrix factorization hashing for multimodal data. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA. 2014. 2083–2090.
|
| [5] |
Zhou JL, Ding GG, Guo YC. Latent semantic sparse hashing for cross-modal similarity search. Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval. Montreal, QC, Canada. 2014. 415–424.
|
| [6] |
Kumar S, Udupa R. Learning hash functions for cross-view similarity search. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence. Barcelona, Spain. 2011. 1360–1365.
|
| [7] |
Zhang DQ, Li WJ. Large-scale supervised multimodal hashing with semantic correlation maximization. Proceedings of the 28th AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada. 2014. 2177–2183.
|
| [8] |
Lin ZJ, Ding GG, Hu MQ, et al. Semantics-preserving hashing for cross-view retrieval. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA. 2015. 3864–3872.
|
| [9] |
Cao Y, Long MS, Wang JM, et al. Deep visual-semantic hashing for cross-modal retrieval. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. East Lansing, MI, USA. 2016. 1445–1454.
|
| [10] |
Jiang QY, Wu JL. Deep cross-modal hashing. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 3270–3278.
|
| [11] |
Deng C, Chen ZJ, Liu XL, et al. Triplet-based deep hashing network for cross-modal retrieval. IEEE Transactions on Image Processing, 2018, 27(8): 3893-3903. DOI:10.1109/TIP.2018.2821921 |
| [12] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
| [13] |
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lile, France. 2015. 448–456.
|
| [14] |
Huiskes MJ, Lew MS. The Mir flickr retrieval evaluation. Proceedings of the 1st ACM International Conference on Multimedia Information Retrieval. British Columbia, Vancouver, BC, Canada. 2008. 39–43.
|
| [15] |
Escalante HJ, Hernández CA, González JA, et al. The segmented and annotated IAPR TC-12 benchmark. Computer Vision and Image Understanding, 2010, 114(4): 419-428. DOI:10.1016/j.cviu.2009.03.008 |
| [16] |
Lin TY, Maire M, Belongie S, et al. Microsoft COCO: Common objects in context. Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland. 2014. 740–755.
|
| [17] |
Russakovsky O, Deng J, Su H, et al. ImageNet large scale visual recognition challenge. International Journal of Computer Vision, 2015, 115(3): 211-252. DOI:10.1007/s11263-015-0816-y |
 2021, Vol. 30
2021, Vol. 30












