截至2020年, 我国抽水蓄能电站装机规模将达4000万千瓦^[1]. 随着抽水蓄能电站规模的日益增大以及新技术、新方法的逐步应用和成熟, 为抽水蓄能电站进一步实现智能化、自动化提供了需求背景和技术基础. 目前国内主要发电集团、设备制造商、科研所等相关单位均进行了深入积极研究, 并陆续建成实现了数据收集、控制调度、生产管理等较完备的自动化体系^[2]. 然而由于终端设备的算力存在不足, 导致抽水蓄能电站的物联网体系智能化程度不高. 云计算技术在一定程度上能够缓解终端设备计算资源不够的问题^[3], 但是由于物理距离的限制, 云计算技术会导致较高的任务处理时延. 为此, 边缘计算模式应运而生, 边缘计算可以满足相关应用场景的低时延需求^[4]. 边缘计算的主要特点是将移动计算、网络控制和存储迁移到网络边缘, 以便在资源有限的移动设备上实现计算密集型和延迟关键性应用. 与云计算相比, 边缘计算可以实现更低延迟、移动设备的能耗节省、上下文感知计算以及移动应用隐私和安全的增强^[5].

边缘计算技术包含计算卸载、资源管理、移动性管理以及安全与隐私保护4个方面, 其中计算卸载是将移动终端的计算任务卸载到边缘服务器上, 它是边缘计算的关键环节^[6]. 并且, 计算卸载是边缘服务器进行数据处理的有效方式, 通过计算卸载策略实现数据分流, 有效利用边缘服务器和本地计算资源, 增加数据处理效率, 减少任务处理时延. 边缘计算技术通过计算卸载算法对复杂的计算任务进行分配, 被分配后的数据利用边缘附近计算资源而不是利用本地资源, 大大减少了中心云的数据处理压力^[7].

本文利用边缘计算的概念, 将边缘计算的理念应用到抽水蓄能电站系统里, 提出一种基于边缘计算的卸载算法. 首先, 针对终端设备不同的任务属性信息进行优先级预处理, 在边缘控制器端基于深度Q网络制定任务卸载决策, 然后将终端设备的计算任务迁移到边缘服务器处进行处理, 以获得更低的任务处理时延, 并保证任务卸载决策的长期有效性, 从而大幅提高抽水蓄能电站中数据处理相关工作的有效性与抽水蓄能电站物联网管理体系的智能化程度.

1 国内外研究现状

目前国内外大量研究者对边缘计算和深度Q网络进行了深入研究. 文献[8]中作者提出了一种动态的端边协同任务调度算法, 联合优化卸载过程中的执行时延和传输能耗, 动态调整终端任务调度策略. 文献[9]中, 作者通过数值优化算法, 提供了任务卸载过程中的最优解. 文献[10]针对计算任务无差别向边缘服务器卸载的情况, 基于一维搜索算法提出最优卸载决策. 但是对于动态变化的物联网环境来说, 文献[9,10]的卸载决策不能保证长期有效性. 在文献[11]中提出了一种基于DQN的多用户单小区计算卸载与资源分配算法, 联合优化任务执行时延与能耗的加权和, 实现了任务总成本的下降.

随着抽水蓄能电站规模的不断扩大以及物联网技术的不断应用, 抽水蓄能电站正在进一步地向智能化的体系转变. 文献[12]对泛在电力物联网下的抽水蓄能电站智慧管理模式进行了思考, 其中泛在物联网提出了全息感知、泛在连接、开放共享、融合创新的技术路线, 对目前抽水蓄能电站的智能化发展进一步提供了思路. 文献[13]提出一种多能耦合协同的新一代抽水蓄能电站, 极大地增强了传统抽水蓄能电站的综合效益性能. 文献[14]研究了关于抽水蓄能电站自动化系统智能化发展, 分析了自动化系统框架的结构, 实现将抽水蓄能电站各并联电力机组加以高度集成化、互动化控制, 使其在智能电网中发挥更为显著的应用效用. 文献[15]中基于国网新源控股有限公司正在建设的物联网架构, 对智慧管控平台进一步提出了设想, 该平台建设并完善了信息采集、数据处理、智能分析等功能, 形成了共享、互联的智能管控系统. 文献[16]针对能源管理, 信息管理和安全性等多个不同领域的电网架构进行了分析, 同时对边云协同技术的应用进行了全面调研, 论证了相应技术在这些领域的效性与可靠性, 为智能电网的发展指明了方向. 文献[17]将集成信息系统引入抽水蓄能电站的生产管理中做出了尝试, 并提出相应的技术方案,有效解决抽水蓄能电站的生产管理任务. 文献[18]介绍了小型光伏抽水蓄能系统的设计和频率控制, 提出了系统的双重用途和智能控制方法. 其中储罐设计计算是针对传统用水进行的, 进行计算是为了预测每个设计情况下的发电量, 进而在不同运行条件下, 采用非线性PID控制器和神经网络进行频率控制.

2 系统模型

本文所提出的系统模型应用于抽水蓄能电站生产活动中, 该系统包含电站物联网终端设备及边缘设备. 在智能电网的应用场景中, 电网对抽水蓄能机组的安全等级、响应方式及速度等提出了新的要求, 电站物联网终端设备会产生各种各样的计算密集型任务. 如果按照传统的方式将计算任务上传至云服务器, 会产生较大的处理时延, 影响电站的正常运转. 为优化处理程序, 减小任务执行时延, 本文将计算任务卸载至边缘服务器进行处理. 如图1所示, 该系统包含3个层面: 终端层, 边缘层和控制层. 其中, 终端层包含大量进行数据采集任务的传感器以及对数据进行汇总的终端设备, 边缘层为一组高计算性能的边缘服务器. 在该系统架构中, 终端设备将收集的数据汇总并形成对应的计算任务后, 由于受限与自身较弱的计算能力, 终端设备会将最大容忍时延、计算复杂度、数据量大小等任务属性信息上传至边缘控制器, 之后由边缘控制器制定相应的卸载算法决定哪些终端设备的计算任务可以卸载至边缘服务器.

2.1 终端任务模型

本文假设抽水蓄能电站厂区的终端设备集合表示为 $K = \{ 1,2, \cdots ,k, \cdots, K\}$ , 边缘层的边缘服务器集合表示为 $E = \{ 1,2, \cdots, e, \cdots, E\}$ , 第k个终端设备在第i个时隙产生的计算任务表示为 ${C_{i,k}} = ({V_{i,k}},{D_{i,k}},{\Gamma _{i,k}},{P_{i,k,e}})$ , 其中 ${V_{i,k}}$ 表示任务的计算复杂度, 单位为比特/轮(bit/cycle), ${D_{i,k}}$ 表示计算任务的数据量大小, 单位为比特(bit), ${\Gamma _{i,k}}$ 表示计算任务的最大可容忍时延, 其单位为毫秒(ms), ${P_{i,k}}$ 为边缘控制器给该任务制定的卸载决策, 其中 ${P_{i,k,e}} = $ $ 0$ 表示本地执行, ${P_{i,k}} = 1$ 表示计算任务被卸载至边缘服务器e执行. 同时我们设定厂区的终端设备本地计算能力为 $f_k^l$ , 单位为转/秒(cycle/s). 边缘服务器的功率设为 ${p_e}$ , 计算资源表示为 $F = \{ {f_{e,k}}|e \in E,k \in K\} $ , 且满足约束 $\displaystyle\sum\limits_k^K {{f_{e,k}}} \le {f_e}$ , 其中 ${f_{e,k}} > 0$ 表示终端设备k卸载到边缘服务器e后被分配的计算能力, 单位为转/秒(cycle/s). 最后本文假设无论是在本地或者卸载执行, 计算任务的相关属性信息保持不变, 一旦任务执行时延超过最大容忍时延, 则将该次任务标记为执行失败.

2.2 本地计算模型

如果厂区的终端设备k选择本地执行任务 ${C_{i,k}}$ , 则计算任务的本地执行时延可表示为:

$ T_k^l = \sum\limits_e^E {\frac{{(1 - {P_{i,k,e}}){D_{i,k}}}}{{f_k^l}}} ,\;\forall k \in K $

(1)

在本地计算中, 任务的执行速率可以表示为:

$ {R_l} = \frac{{f_k^l}}{{{D_{i,k}}}} $

(2)

同时由文献[19]可知, 若终端设备的能耗系数为 $\alpha $ , 则终端设备k执行任务的能耗可以表示为:

$ E_k^l = \sum\limits_e^E \alpha (1 - {P_{i,k,e}}){D_{i,k}}{\left( {f_k^l} \right)^2},\;\forall k \in K $

(3)

2.3 卸载计算模型

若终端设备k采用卸载方式执行计算任务, 则该过程可分为3段: 任务上传、任务执行、执行结果下载.

首先在任务上传过程中, 本文将当前终端设备上传带宽设定为 ${B_k}$ ,信道传输噪声设定为 ${N_0}$ , 无线信道增益设定为 ${g_k}$ , 终端设备发射功率为 ${p_k}$ , 则上传速率可表示为:

$ {R_O} = {B_k}{\log _2}\left( {1 + \frac{{{p_k}{g_k}}}{{{N_0}\dfrac{{{B_k}}}{K}}}} \right) $

(4)

上传时延表示为:

$ T_k^{o_{\rm trans}} = \sum\limits_e^E {\frac{{{P_{i,k,e}}{D_{i,k}}}}{{{R_O}}}} ,\;\forall k \in K $

(5)

在任务执行过程中, 计算任务的执行时延我们可以表示为:

$ T_k^{o_{\rm exe}} = \sum\limits_e^E {\frac{{{P_{i,k,e}}{D_{i,k}}}}{{{f_{e,k}}}}} ,\;\forall k \in K $

(6)

本文将任务结果下载过程的执行时延忽略不计, 因此终端设备k在任务卸载过程中的执行时延可以表示为:

$ T_k^o = T_k^{o_{\rm trans}} + T_k^{o_{\rm exe}} $

(7)

能耗表示为:

$ E_k^o = {p_e}T_k^{o_{\rm exe}} + {p_k}T_k^{o_{\rm trans}} $

(8)

3 基于边缘计算的任务分发卸载方案 3.1 任务优先级划分

由于计算任务属性的不同, 其所需的计算资源也不一样, 本文基于层次分析法(Analytic Hierarrchy Process, AHP)^[20]对计算任务进行预处理, 给计算复杂度更高、最大容忍时延更小的计算任务赋予更高的权重, 从而为边缘控制器制定卸载决策更合理的依据.

本文将计算任务复杂度 ${V_{i,k}}$ 、最大容忍时延 ${\Gamma _{i,k}}$ 、数据量大小 ${D_{i,k}}$ 作为计算任务权重系数的3个考量因素, 其重要程度依次下降. 首先, 可以得到评价因素判断矩阵 ${{A}} = {({a_{ij}})_{3\times 3}}$ , 如式(1)所示:

$ {a_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{{{a_{ji}}}} = n,\;\;n = \{ 1,2, \cdots, 9\} } \\ {1,\;\;i = j} \end{array}} \right. $

(9)

然后根据方根法可以求得矩阵对应的权重向量元素. 如式(10)所示:

$ u_k^i = \frac{{\sqrt[K]{{\displaystyle\mathop \Pi \limits_{j = 1}^K {a_{ij}}}}}}{{\displaystyle\sum\limits_{i = 1}^K {\sqrt[K]{{\mathop \Pi \limits_{j = 1}^K {a_{ij}}}}} }} $

(10)

根据式(10), 可以得到厂区所有终端设备计算任务的权重矢量矩阵:

$ {{U}} = \left[ {\begin{array}{*{20}{c}} {u_1^1}&{u_1^2}&{u_1^3} \\ {u_2^1}&{u_2^2}&{u_2^3} \\ {}&{...}&{} \\ {u_K^1}&{u_K^2}&{u_K^3} \end{array}} \right] $

(11)

接着如式(9)构造出目标层与准则层之间的判断矩阵 ${B_1},{B_2},{B_3} = {({a_i}_j)_{k\times k}}$ , 并求出判断矩阵B的权重向量, 如式(12)所示:

$ {\Delta ^i} = \dfrac{{\sqrt[3]{{\mathop \Pi \limits_{j = 1}^3 {a_{ij}}}}}}{{\displaystyle\sum\limits_{i = 1}^3 {\sqrt[3]{{\mathop \Pi \limits_{j = 1}^3 {a_{ij}}}}} }} $

(12)

最后, 根据式(13)可得到厂区所有终端设备计算任务的权重向量:

$ {{W}} = {{U}} \times {{\Delta }} = \left( {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^3 {U_1^i{\Delta ^1}} } \\ {\displaystyle\sum\limits_{i = 1}^3 {U_2^i{\Delta ^2}} } \\ {\vdots} \\ {\displaystyle\sum\limits_{i = 1}^3 {U_K^i{\Delta ^i}} } \end{array}} \right) $

(13)

3.2 问题建立

在3.1节中, 本文选取了计算最大容忍时延、任务复杂度、数据量大小3个因素对终端的计算任务进行了预处理, 其重要性依次下降, 得到了对应的计算权重. 因此考虑以边缘服务器计算资源及能耗为约束、以时延为优化目标建模时, 具体问题可以如下表示:

$\left\{ \begin{split} & \min \left( {\left( {{w_k}} \right)\sum\limits_{k = 1}^K {\left( {T_k^o + T_k^l} \right)} } \right) \\ & {\rm{s.t.}}\left\{\begin{array}{*{20}{l}} {{C1:}}{P_{i,k,e}} \in \left\{ {0,1} \right\} \\ {{C2:}}\displaystyle\sum\limits_k^K {{f_{e,k}}} \le {f_e} \\ {{C3:}}{f_{e,k}} \ge 0 \\ {{C4:}}\displaystyle\sum\limits_k^K {(E_k^l + E_k^o)} \le {E_{\rm constraint}} \end{array} \right. \end{split} \right. $

(14)

其中, 约束2 (C₂)、约束4 (C₄)分别表示边缘服务器分配的计算资源以及任务执行总能耗不可超过限定值.

3.3 基于深度强化学习的卸载决策制定

式(13)是一个典型的混合整数非线性规划问题, 多项式时间内无法用常规的数值优化方法求出^[21]. 对于需要动态监测的抽水蓄能电站而言, 本文考虑采用深度强化学习对问题进行求解, 将边缘控制器作为智能体, 协调厂区内的所有边缘服务器. 在本节中, 我们首先对强化学习三要素进行建模.

(1)状态

在本文中, 考虑到边缘服务器剩余计算资源随着终端计算任务卸载决策的变化而变化, 将边缘服务器在每个时隙开始时具有的剩余计算资源设定为当前状态, 表示如式(15):

$ S({\rm{t}}) = \{ {s_1}(t),{s_e}(t), \cdots, {s_E}(t)\} $

(15)

其中, $S({\rm{t}})$ 表示第t个时隙的状态空间, ${s_e}(t)$ 表示边缘服务器e在第t个时隙开始时剩余的计算资源.

(2)动作

本文训练算法采用Double DQN, 其核心迭代算法使用的是Q学习算法^[22]. 由式(13)可知, 本文主要优化的变量分别为边缘控制器的卸载决策以及边缘服务器的计算资源分配决策, 因此将动作向量定义为;

$ A(t) = \{ P,{f_1}, \cdots ,{f_k}, \cdots, {f_K},p_1, \cdots ,{p_k}, \cdots ,{p_K}\} $

(16)

其中, P表示边缘控制器制定的卸载决策向量, ${f_k}$ 表示边缘服务器分配给第k个终端设备的计算资源, ${p_k}$ 表示第k个终端的发射功率.

(3)奖励

边缘控制器可以通过奖励值的期望来对未来动作进行规划, 其目标是最大化当前奖励值. 结合本文应用场景, 我们计算任务的本地执行速率与上传速率的加权和作为奖励函数, 定义如下:

$ R(s,a) = {I_l}{R_l} + {I_o}{R_o} $

(17)

接下来可以得到该问题的长期累积奖励, 表示为:

$ {Q_\pi }(s,a) = {E_\pi }\left[ {\sum\limits_{t = 1}^T {{\beta ^{t - 1}}R} } \right] $

(18)

在本文中, 动作、状态值、奖励值存放于回访记忆单元中, 通过Q学习算法经历多个迭代过程来反复训练Q值网络, 最后得到最佳卸载决策, 可以表示为:

$ {\pi ^*} = \arg \mathop {\max }\limits_{a \in A} {Q_\pi }(s,a) $

(19)

本文算法流程描述如算法1所示.

算法1. 任务卸载算法

输入: 终端设备计算任务的计算复杂度V、数据总量D及最大容忍时延 $\scriptstyle\Gamma $ , 终端设备的上传功率p. 根据式(9)~式(13)得到每个计算任务的优先级W, 即计算任务的计算资源分配权重.

输出: 终端设备计算任务的卸载决策P.

1. 初始化经验池存储空间容量并且用随机权重 $\scriptstyle\theta $ 初始化动作-价值函数 $\scriptstyle{Q_\pi }(s,a)$ .

2. for each episode:

3.　　　初始化状态 $\scriptstyle S({{t} })$ .

4.　　　for each iteration:

5.　　　　　以 $\scriptstyle \varepsilon $ 的概率选择随机动作, 否则选择潜在回报最大的动作 $\scriptstyle a = \max Q(s,a;\theta )$ .;

6.　　　　　执行动作a, 得到奖励值R与S'.

7.　　　　　将放入经验池中, 并从经验池中选取最小批次数量的经验对Double DQN神经网络进行训练以更新权值 $\scriptstyle \theta $ .

8.　　　　　每隔L步, 将评估网络的权值 $\scriptstyle\theta $ 复制给目标网络.

9.　　　　　如果是终止状态, 结束本轮迭代过程

10.　　　end for

11. end for

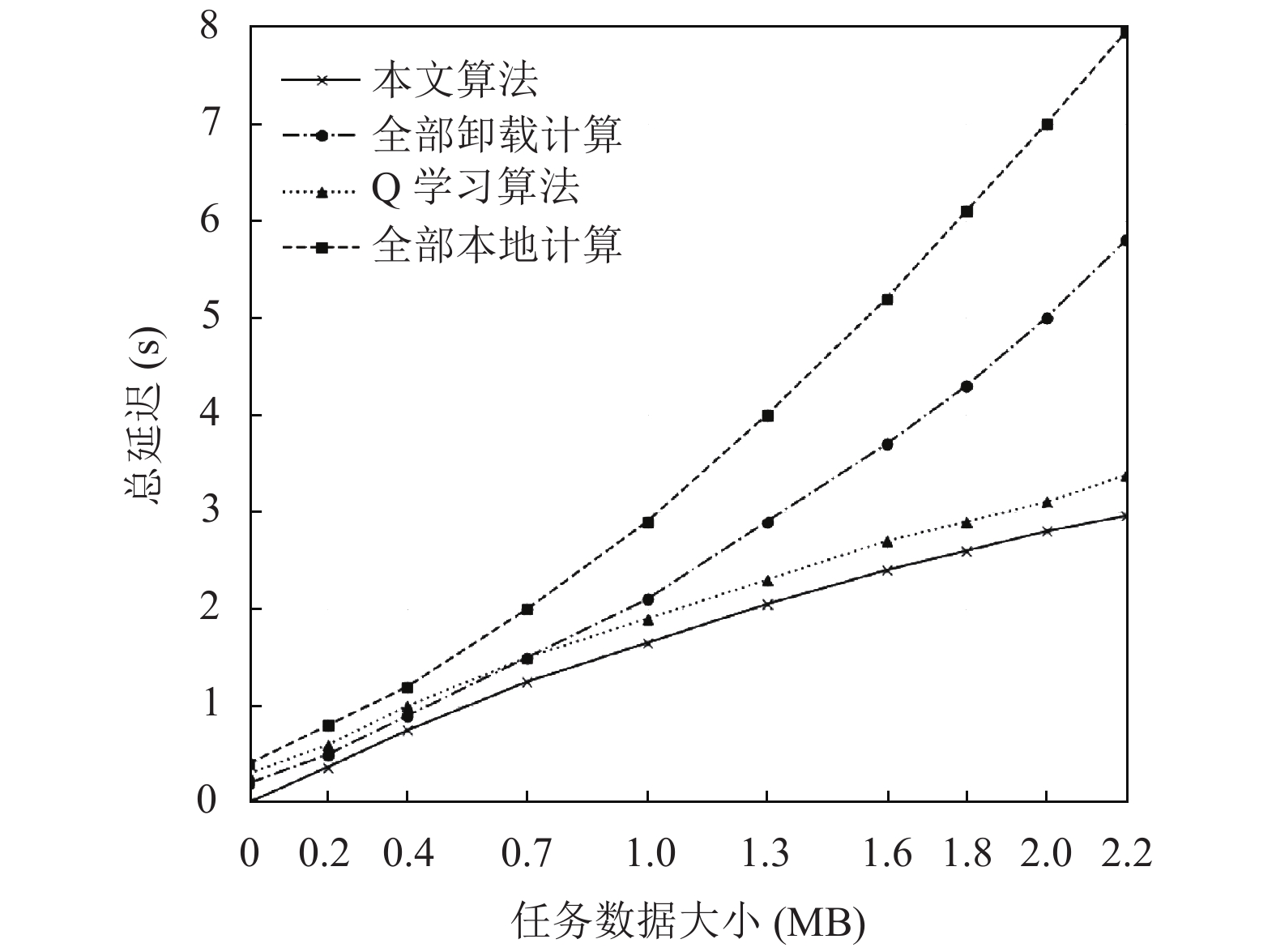
4 实验分析

本节通过Python编程语言对本文算法进行仿真以评估算法性能. 本文考虑抽水蓄能电站中有单小区多边缘服务器场景. 基站覆盖范围内部署一个边缘服务器, 且覆盖范围内抽水蓄能电站厂区的终端设备均匀分布, 其中边缘控制器能够调度所有基站及边缘服务器资源. 假定每个基站覆盖范围为1000 m, 每个终端设备计算能力为1 GHz, 边缘服务器最大计算资源为5 GHz. 终端设备计算功率为3 W, 发射功率为0.3 W, 携带的计算任务数据大小(以兆比特为单位)服从[0,2]的均匀分布, 计算任务复杂度(以兆轮为单位)服从[900,1100]的均匀分布. 下面将本文算法分别与全部本地计算、全部卸载计算、Q学习算法进行比较.

图2为平均总延迟与抽水蓄能电站厂区的终端设备待处理的计算任务数据大小的关系. 任务的总延迟随着输入数据大小的增加而增加. 在数据量最大时, 本文算法相比较于Q学习算法延迟减少了300 ms. 分析可知, 一方面我们引入了边缘计算, 提高了系统的计算容量, 能够优化任务执行效率. 另一方面, 基于DQN算法, 可以根据环境变化自适应制定卸载决策, 最大化利用系统资源, 并保证卸载决策的长期有效性, 对抽水蓄能电站的物联网体系智能化建设有着较大的帮助.

在图3中, 本文以任务复杂度作为变量, 对Q学习算法和本文算法进行了比较. 从图3可以看出, 随着任务计算复杂度的上升, 卸载决策的制定变得更加艰难, 任务执行失败概率都随之增加. 但是本文算法的任务执行失败概率低于Q学习算法, 同时本文算法执行失败率的上升趋势也明显低于Q学习算法, 这是因为本文算法对抽水蓄能电站厂区终端设备所有的计算任务做了自适应优先级预处理, 给优先级更高的计算任务分配了更多的计算资源, 使计算任务执行成功概率更高, 提高卸载决策正确率, 有效减小了厂区终端设备计算任务执行时延, 从而能够使得抽水蓄能电站能够在边缘侧完成一系列控制调度、自动化监测等时延敏感型应用的部署.

5 结论与展望

面向抽水蓄能电站中终端设备最大容忍时延及最大能耗约束的情况, 本文提出了一种基于边缘计算的任务卸载算法. 通过引入边缘计算, 在完成终端自身携带计算任务的优先级处理后, 边缘控制器通过DQN算法制定卸载决策, 以最小化终端设备的任务执行时延. 通过对该算法的大量仿真分析及数值验证, 本文所提出的任务卸载算法在不同的情景下都优于传统的方案. 今后的研究将会考虑对DQN的训练算法进行相应改进, 同时抽水蓄能电站中复杂的无线电干扰等环境因素也会加以综合考虑.