基于倒位变异的蜉蝣优化算法

引用本文

陈伟超, 符强. 基于倒位变异的蜉蝣优化算法. 计算机系统应用, 2021, 30(8): 157-163.http://www.c-s-a.org.cn/1003-3254/8034.html

Chen WC, Fu Q. Mayfly Optimization Algorithm Based on Inversion Variation. Computer Systems and Applications, 2021, 30(8): 157-163(in Chinese).http://www.c-s-a.org.cn/1003-3254/8034.html

基于倒位变异的蜉蝣优化算法

陈伟超, 符强

宁波大学科学技术学院, 宁波 315300

收稿日期：2020-11-12; 修改日期：2020-12-12; 采用时间：2021-01-06; csa 在线出版时间：2021-07-31

基金项目：宁波市自然科学基金(202003N4159); 国家级大学生创新创业训练计划(202013277008)

通讯作者：符强, E-mail: fuqiang@nbu.edu.cn.

摘要：蜉蝣算法(Mayfly Algorithm, MA)作为一种新型群智能优化算法, 具有较好的寻优性能. 但在高维非线性复杂问题上, 蜉蝣算法依然容易出现早熟收敛现象. 本文提出一种基于倒位变异的蜉蝣算法(Inversion Variation Mayfly Algorithm, IVMA), 改变原算法在变异上的操作, 随机选择个体的随机维度向全局最优个体的随机维度靠近, 同时利用精英策略保留进化成果. 利用倒位操作, 将最优个体某一维度段内位置发生倒转, 提高了算法跳出局部最优的能力. 通过对10个测试函数的结果分析, 表明本文所提出的算法具有较好的收敛精度, 收敛性能得到了提高.

关键词: 群智能算法收敛蜉蝣算法倒位变异突变

Mayfly Optimization Algorithm Based on Inversion Variation

CHEN Wei-Chao, FU Qiang

College of Science & Technology Ningbo University, Ningbo 315300, China

Foundation item: Natural Science Foundation of Ningbo City (202003N4159); National College Student Innovation and Entrepreneurship Training Program (202013277008)

Abstract: The Mayfly Algorithm (MA), which serves as a new swarm intelligence optimization algorithm, proves to perform well in optimization. However, when it comes to complex problems related to high dimensions and linearity, MA is still prone to premature convergence. Thus, a new mayfly algorithm based on inversion variation (Inversion Variation Mayfly Algorithm, IVMA) is proposed. IVMA, which changes the operation of the original MA on mutation, stochastically selects the random dimension of an individual to approach that of the global optimal individual. In addition, it retains the evolution results with the elite strategy. The inversion operation is used to reverse the position of the optimal individual in a certain dimension segment, which enhances the ability of the algorithm to jump out of the local optimum. The results from ten test functions indicate that IVMA has high convergence accuracy and improved convergence performance.

Key words: swarm intelligence algorithm convergence mayfly algorithm inversion variation mutation

随着社会的发展, 出现了许多复杂的优化问题亟待解决, 传统的数学工具已经不在适用于求解这些问题. 随着计算智能的发展, 出现了群智能算法^[1]. 群智能算法是一种新兴的演化计算技术, 相比于其它传统优化算法能更快的发现复杂优化问题的最优解, 已成为越来越多研究者的关注焦点. 群智能算法原理简单, 寻优能力良好. 通过对群智能算法的不断改进和优化, 使得群智能算法应用面越来越广, 粒子群算法^[2]等已经广泛应用于非线性复杂约束规划、作业调度优化等实际工程中.

蜉蝣算法(Mayfly Algorithm, MA)^[3]是2020年新提出的群智能优化算法. MA算法根据蜉蝣的活动方式和习性而编写. 其中雄蜉蝣成群的聚集, 每只雄蜉蝣的位置都是根据自己和邻居的经验来调整, 雄蜉蝣通过婚礼舞蹈吸引雌蜉蝣进行交配.

MA算法把雄蜉蝣的位置移动看作算法的寻优过程, 同时引入了婚礼舞蹈系数和随机飞行系数, 有助于算法跳出局部最优. 但在高维非线性复杂问题中, MA算法的全局收敛性能较差. 本文将倒位变异和突变结合, 提出了一种基于倒位变异的蜉蝣算法(Inversion Variation Mayfly Algorithm, IVMA), 以提高算法在高维非线性复杂问题的收敛精度. 并通过随机抽取的10个50维度benchmark标准测试函数对算法性能进行验证.

1 标准蜉蝣优化算法简介

MA^[3]算法是一种求解优化问题的群智能优化算法, 该算法受蜉蝣飞行行为和交配过程的启发. 其中MA算法结合了粒子群算法(PSO)^{[4, 5]}、遗传算法(GA)^[6]和萤火虫算法(FA)^[7]的主要优点, 提高了算法寻优能力, 使得MA算法具有较好的寻优能力, 但在高维非线性复杂问题上, MA算法跳出局部最优的能力较差, 容易出现早熟收敛的现象. 使得算法在多峰函数中表现较差. 具体的计算方法如下:

设有一个D维问题, MA算法根据蜉蝣的位置来求出最优解, 第i个蜉蝣的位置x_i={x₁, x₂, x₃, …, x_D}对应速度为V_i={V₁, V₂, V₃, …, V_D}.

1.1 雌蜉蝣更新

雌蜉蝣的速度更新: 雌蜉蝣不会像雄蜉蝣一样成群结队, 当雌蜉蝣被雄蜉蝣吸引时, 会向雄蜉蝣靠近, 否则雌蜉蝣会随机飞行. 它们的速度计算如下:

$v_{ij}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {g*v_{ij}^t + {a_2}{e^{ - \beta r_{mf}^2}}\left( {x_{ij}^t - y_{ij}^t} \right), \;{\rm{if}}\;f\left( {{y_i}} \right) > f\left( {{x_i}} \right)} \\ {g*v_{ij}^t + fl*r, \;{\rm{if\; }}f\left( {{y_i}} \right) \le f\left( {{x_i}} \right)} \end{array}} \right. \!\!\!\!\!\!$

(1)

其中, V_ij^t+1是雌蜉蝣i在维度j中的位置, a₂是固定的可见性系数, rmf是雄蜉蝣和雌蜉蝣之间的笛卡尔距离( ${x_i} - {X_i} = \sqrt {\displaystyle\mathop \sum \limits_{j = 1}^n {{\left( {{x_{ij}} - {X_{ij}}} \right)}^2}} $ 为笛卡尔距离计算公式), fl是随机飞行系数, r是[−1, 1]区间内的一个随机数, iter是当前迭代次数, iter_max为最大迭代次数. g是动态惯性系数, 更新公式如下:

$g = {g_{\max}} - \left( {\frac{{{g_{\max}} - {g_{\min}}}}{{ite{r_{\max}}}}} \right)*iter$

(2)

雌蜉蝣的位置移动通过蜉蝣所在位置加上蜉蝣获得的速度V_i^t+1来改变.

$y_i^{t + 1} = y_i^t + v_i^{t + 1}$

(3)

其中, y_i^t为雌性蜉蝣i在时间步长t时在搜索空间上的位置, 蜉蝣在搜索空间中飞行, 因此位置具有限制y_ij∈(y_min, y_max).

1.2 雄蜉蝣更新

雄蜉蝣的速度更新: 在表演婚礼舞蹈时, 雄蜉蝣不能产生出很快的速度, 但它们会不断地移动. 因此, 雄性蜉蝣i的速度计算如下:

$v_{ij}^{t + 1} \!=\! \left\{\!\!\!\!\! {\begin{array}{*{20}{l}} {g*v_{ij}^t \!+\! {a_1}{e^{ - \beta r_p^2}}\left( {pbes{t_{ij}} \!-\! x_{ij}^t} \right) + {a_2}{e^{ - \beta r_g^2}}\left( {gbes{t_j} - x_{ij}^t} \right), } \\ \;\;\;\;\;\;\;\;\;\;\;\;{{\rm{if\; }}f\left( {{x_i}} \right) > f\left( {GlobalBest} \right)} \\ {g*v_{ij}^t + d*r, \;{\rm{if\; }}f\left( {GlobalBest} \right) \le f\left( {{x_i}} \right)} \end{array}} \right. $

(4)

其中, V_ij^t+1是雄蜉蝣i在维度j上的速度, a₁, a₂分别是正吸引系数, 用于衡量认知和社会贡献. d是舞蹈系数, r是[−1, 1]区间内的一个随机数, g是动态惯性系数, GlobalBest是全局最优个体.

此外pbest是蜉蝣i去过最好的位置, 在下一个时间步长中, 个体最优位置为:

$pbes{t_i} = \left\{ {\begin{array}{*{20}{l}} {x_i^{t + 1},&{\rm{if}}\;f\left( {x_i^{t + 1}} \right)}{ < f\left( {pbes{t_i}} \right)}\\ {{\text{保持不变}},}&{\text{其他}} \end{array}} \right. $

(5)

其中, 全局最优位置gbest的定义如下

$\begin{split} gbest =& \left\{ {pbes{t_1},pbes{t_2}, \cdots, pbes{t_n}{{|f}}\left( {{{cbest}}} \right)} \right\}\\ =& {\rm{min}}\left\{ {{{f}}\left( {{{pbes}}{{{t}}_{\rm{1}}}} \right),{{f}}\left( {{{pbes}}{{{t}}_{\rm{2}}}} \right), \cdots ,{{f}}\left( {{{pbes}}{{{t}}_{{N}}}} \right)} \right\} \end{split}$

(6)

雄蜉蝣的位置的移动通过在蜉蝣所在位置加上蜉蝣获得的速度来改变.

$x_i^{t + 1} = x_i^t + v_i^{t + 1}$

(7)

其中, x_i^t+1为雄蜉蝣i在时间步长t时在搜索空间上的位置, 雄蜉蝣在搜索空间中飞行, 因此位置具有限制x_ij∈(x_min, x_max).

当更新一个远离全局最佳位置或个人最佳位置的蜉蝣的速度时可能会出现蜉蝣飞出问题空间的情况. 根据蜉蝣的生活习性, 蜉蝣不会一直增加速度. 假设每个蜉蝣能够产生一个指定的最大速度V_max. 因此, 速度调整为:

$ {v}_{ij}^{t+1}=\left\{ \begin{array}{l}{V}_{\max}, \;\;{\rm{if}} \;{v}_{ij}^{t+1}>{V}_{\max}\\ -{V}_{\max},\;\; {\rm{if}}\;{v}_{ij}^{t+1}<-{V}_{\max}\end{array}\right.$

(8)

其中, V_max=rand*(x_max−x_min), 其中rand∈(0, 1].

1.3 蜉蝣交配

在一个种群中, 雄雌蜉蝣按照适应值选择配对个体进行交配, 适应值最优的雄蜉蝣和适应值最优的雌蜉蝣进行交配, 依此类推. 交配结果是产生两个子代, 其产生公式如下:

$offspring_1 = L*male + \left( {1 - L} \right)*female$

(9)

$offspring_2 = L*female + \left( {1 - L} \right)*male$

(10)

其中, L是[−1, 1]之间的一个随机数, 子代的初始速度设定为0.

1.4 蜉蝣变异

为了处理可能导致出现的最优值是局部最优而不是全局最优的早熟收敛情况, 在, 将正态分布的随机数加到所选子代蜉蝣中进行突变, 子代蜉蝣突变公式如下:

$offsprin{g_n} = offsprin{g_n} + \sigma {{N}}\left( {0, 1} \right)$

(11)

其中, $\sigma $ 是正态分布的标准偏差. N(0, 1)是平均值为0, 方差为1的标准正态分布. 变异个体的数量为round(0.05*雄蜉蝣数量).

婚礼舞蹈系数与随机飞行系数也会随迭代次数减少, 公式如下:

${d_t} = {d_0}*{d_{{\rm{damp}}}^t}$

(12)

$f{l_t} = f{l_0}*f{l_{{\rm{damp}}}^t}$

(13)

其中, d_t与fl_t为t时刻的婚礼舞蹈系数和随机飞行系数, d_damp与fl_damp是婚礼舞蹈系数和随机飞行的衰减参数.

2 基于倒位变异的蜉蝣算法(Inversion Variation Mayfly Algorithm, IVMA)

面对高维非线性复杂问题时, MA算法容易陷入局部最优区域, 发生进化停滞的情况. 如图1所示在函数Griewank中MA算法较早的出现了陷入局部最优的现象, 使得种群进化停滞.

图 1 Griewank函数

对于MA算法存在的缺陷, 本文提出的IVMA算法通过对最优个体进行倒位变异操作, 使得IVMA算法具有较好全局搜索能力. 对倒位变异策略产生的新个体使用精英策略保留进化成果. 改变原算法在变异上的操作, 提高IVMA算法在高维复杂问题中的收敛精度.

2.1 倒位变异机制

由于MA算法在算法收敛过程中容易出现早熟收敛的问题, IVMA算法在为了避免在算法后期陷入局部最优, 提高算法摆脱局部极值点的能力, 引用了倒位变异机制^[8]. 在进行一轮种群进化之后, 当种群的适应值连续两代的差值小于某个阈值时(阈值设于10⁻³), 对蜉蝣的最优个体进行倒位变异, 以增强种群的多样性, 提高算法的全局收敛性能.

倒位变异的具体操作如下, 对最优个体GlobalBest进行倒位操作. 首先在[1, D]之间随机选取两个整数p和q, 设p<q, p, q为最优个体的不同维度, 将p, q两个维度之间的GlobalBest位置进行倒序, 如当p为10, q为20时, GlobalBest的10维的位置和20维的位置进行交换, GlobalBest的11维的位置和19维的位置进行交换. 以此进行类推, 则执行倒序操作后得到了新个体, 带入目标函数, 如果产生的新个体比当前全局最优个体更好, 则进行更新, 以此保留种群进化的成果.

利用倒位变异改变GlobalBest在随机维度段p至q之间的位置, 即对选定的维度段内GlobalBest的位置进行倒序操作, 得到的新个体和GlobalBest比较, 使用较优个体对种群进化进行引导. 因为雄蜉蝣的位置是通过自身到过的最好位置和当前全局最优个体GlobalBest的位置进行移动的, 利用经过倒位变异操作的GlobalBest的引导, 使得雄蜉蝣在靠近自身到过的最优位置和当前全局最优位置的过程中具备了找到优于当前全局最优个体的位置的能力.

通过倒位变异机制, 使得IVMA算法具备了良好的找到全局最优的能力, 提高算法了在高维非线性复杂问题中的全局收敛性能.

2.2 突变操作

改变原算法的变异操作, 在进行交配操作后从子代中随机选择一个个体 ${x_i}$ , 产生新个体 $x_i’ $ . 具体操作为, 从子代蜉蝣种群中随机选择一个个体, 通过改变它的单个随机维度的蜉蝣位置来优化算法. ${x_i}$ 中随机的维度d向蜉蝣全局最优个体的随机维度b靠近, 公式如下:

$ {x}_{id}’=GlobalBes{t}_{b}+入\left(GlobalBes{t}_{b}-{x}_{id}\right)$

(14)

其中, b, d∈{1, 2, 3, …,D}分别是随机选取的一个值, λ∈[−1, 1].

通过改变所选子代蜉蝣的随机维度的位置, 提高了种群多样性. 改善了MA算法摆脱局部极值点的能力.

2.3 IVMA算法流程

Step 1. 基本参数设置, 包括种群规模, 最大迭代次数等.

Step 2. 随机产生初始种群, 随机蜉蝣的位置并且设置初始速度为零.

Step 3. 根据式(1), 式(3)分别更新雌蜉蝣的速度和位置, 雌蜉蝣的位置带入目标函数比较适应值, 如果优于个体最优则根据式(5)更新个体最优数据.

Step 4. 根据式(4), 式(7)分别更新雄蜉蝣的速度和位置.

Step 5. 雄蜉蝣的位置带入目标函数比较适应值, 如果优于个体最优则根据(5)更新个体最优数据, 在此基础上, 如果优于全局最优则根据式(6)更新全局最优数据.

Step 6. 对雄雌蜉蝣的适应值根据优劣性进行排序.

Step 7. 根据式(9), 式(10)对蜉蝣进行交配操作产生子代蜉蝣.

Step 8. 根据式(14)对子代蜉蝣进行突变操作.

Step 9. 在进行一次种群进化后, 如果符合阈值条件, 则进行倒位变异操作, 通过比较适应值决定是否更新.

Step 10. 对于蜉蝣适应值进行排序, 取较优解, 保持总群数量不变. 更新舞蹈系数(式(12)), 飞行系数(式(13)), 动态惯性系数(式(2)).

Step 11. 判断是否达到终止条件, 若是则输出最优解: 若否, 则执行Step 3.

3 仿真实验及分析

为了测试IVMA算法的优化性能, 从文献[3]中随机选取了10个标准benchmark函数进行验证. 各函数的参数说明及特征如表1所示.

表 1 测试函数的维度, 搜索空间, 最优值

函数	名称	函数公式	维度	搜索空间	最优值
f1	Sphere	${f_1}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d x_i^2 $	50	[−10, 10]	0
f2	Sum_Squares	${f_2}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d ix_i^2 $	50	[−10, 10]	0
f3	Quartic	${f_8}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d ix_i^4 + rand\left[ {0,1} \right) $	50	[−1. 28, 1. 28]	0
f4	Schwefel2. 20	${f_4}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d ix_i^4 + rand\left[ {0,1} \right) $	50	[−100, 100]	0
f5	Schwefel2. 22	${f_5}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d \|{x_i}\| + \mathop \prod _{i = 1}^d \|{x_i}\| $	50	[−100, 100]	0
f6	Ackley	$\begin{array}{l}{f_6}\left( x \right) = 20 + {\rm{e}} - 20\exp \left[ { - 0.2\sqrt {\dfrac{1}{d}\displaystyle\mathop \sum _{i = 1}^d x_i^2} } \right] - {\rm{exp} }\left[ {\sqrt {\dfrac{1}{d}\displaystyle\mathop \sum _{i = 1}^d \cos (2\pi {x_i})} } \right]\end{array}$	50	[−32, 32]	0
f7	Griewank	${f_7}\left( x \right) = 1 + \displaystyle\mathop \sum _{i = 1}^d \dfrac{{x_i^2}}{{4000}} - \mathop \prod _{i = 1}^d \cos \left( {\dfrac{{{x_i}}}{{\sqrt i }}} \right) $	50	[−600, 600]	0
f8	Qing	${f_8}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d {\left( {{x^2} - i} \right)^2} $	50	[−500, 500]	0
f9	Styblinski-Tang	${f_9}\left( x \right) = \dfrac{1}{2}\displaystyle\mathop \sum _{i = 1}^d \left( {x_i^4 - 16x_i^2 + 5{x_i}} \right) $	50	[−5, 5]	−1958. 3083
f10	Xin-She Yang	${f_{10}}\left( x \right) = \displaystyle\mathop \sum _{i = 1}^d rand\left[ {0,1} \right]*\|{x_i}{\|^i} $	50	[−5, 5]	0

表 1 测试函数的维度, 搜索空间, 最优值

将IVMA算法和MA算法, PSO算法^[9]、优化的蜂群算法(CABC)^[10]进行对比仿真实验. MA算法, PSO算法, CABC算法, IVMA的种群数量均设定为40个, 其中MA算法, PSO算法, CABA算法其他参数设置参考所引文献. IVMA算法具体的参数设置为: 雄雌蜉蝣的数量各为20, 迭代次数2000次, 蜉蝣的舞蹈系数为1, 随机飞行系数为1, d_damp为0. 8, fl_damp为0. 99, g_max为1. 5, g_min为0. 4, a₁ =1, a₂ =1. 5. 为了测试算法在高维非线性复杂问题中的表现, 函数测试维度均为50维, 每个测试函数做100次重复实验进行对比分析, 得出4种算法的最优值, 最差值, 平均值和标准差, 结果如表2所示.

表 2 4种算法对10个函数的计算结果比较

函数	算法名称	最优值	最差值	平均值	标准差
f1	MA	3.0821E–17	3.6320E–16	1.0938E–16	2.4631E–33
	PSO	1.1773E–01	5.3481E–01	2.5328E–01	8.3036E–03
	CABC	4.9689E–07	3.1987E–01	0.021233	2.4657E–03
	IVMA	1.2842E–35	2.6193E–26	4.3992E–28	7.7790E–54
f2	MA	6.5427E–16	2.0141E–14	3.8973E–15	1.0840E–29
	PSO	2.2513E+00	3.4864E+01	9.0318E+00	2.5138E+01
	CABC	9.1355E–03	1.9313E+02	1.3433E+01	1.1272E+03
	IVMA	1.2915E–39	4.5117E–27	4.5931E–29	2.0352E–55
f3	MA	1.1438E–02	5.3129E–02	2.8100E–02	7.2850E–05
	PSO	5.2275E–01	6.1007E+00	1.8058E+00	7.8587E–01
	CABC	1.3448E–03	6.8568E–01	1.1899E–01	1.2173E–02
	IVMA	4.3944E–03	2.8451E–02	1.6064E–02	2.9415E–05
f4	MA	2.9044E–09	1.5442E–06	9.1392E–08	3.2158E–14
	PSO	2.3013E+00	1.6717E+01	8.9675E+00	9.4287E+00
	CABC	2.3517E–03	6.2146E+00	1.0249E+00	9.3417E–01
	IVMA	1.5340E–23	1.8275E–19	1.7415E–20	1.2603E–39
f5	MA	2.4816E–09	4.9781E–06	2.6329E–07	5.0389E–13
	PSO	3.3464E+00	1.8533E+01	8.7750E+00	6.9066E+00
	CABC	7.5295E–03	4.8522E+00	9.8318E–01	1.1313E+00
	IVMA	1.1678E–23	4.3915E–19	1.5582E–20	2.3919E–39
f6	MA	6.4175E-01	3.0971E+00	1.5576E+00	1.4848E–01
	PSO	2.1790E+00	4.1050E+00	3.1619E+00	1.8473E–01
	CABC	3.0470E–03	1.4037E+00	1.2691E–01	3.3081E–02
	IVMA	1.6875E–14	1.1598E–10	1.3041E–12	1.3484E–22
f7	MA	1.9984E–15	1.7182E–01	2.4692E–02	1.1791E–03
	PSO	3.5430E–03	4.2370E–02	1.3000E–02	4.0673E–05
	CABC	3.0705E–10	7.8914E–03	8.7259E–04	1.6926E–06
	IVMA	0.0000E+00	1.9771E–02	3.4441E–04	4.7372E–06
f8	MA	6.1938E–06	3.5653E+01	9.9644E–01	1.9892E+01
	PSO	1.2730E+01	2.2710E+02	4.6568E+01	1.4604E+03
	CABC	9.6487E+03	1.3584E+04	1.1048E+04	6.2492E+05
	IVMA	1.5332E–15	9.8948E–14	1.6274E–14	1.8201E–28
f9	MA	−1.7887E+03	−1.5766E+03	−1.6759E+03	2.2285E+03
	PSO	−1.7698E+03	−1.5431E+03	−1.6488E+03	2.3921E+03
	CABC	−1.9576E+03	−1.4398E+03	−1.9040E+03	5.8253E+03
	IVMA	−1.9583E+03	−1.9117E+03	−1.9573E+03	2.8988E+01
f10	MA	2.2373E–05	3.4020E+00	1.5019E–01	2.1765E–01
	PSO	4.7817E+00	4.2185E+09	7.4109E+07	2.6290E+17
	CABC	2.8916E–05	1.2828E–01	4.1982E–03	1.7544E–04
	IVMA	1.8901E–09	1.2415E–02	1.8594E–04	1.5968E–06

表 2 4种算法对10个函数的计算结果比较

表2显示, 在50维度的10个函数优化测试中, MA算法, PSO算法和ABC算法的搜索能力较差. MA算法, PSO算法和CABC没有一个函数获得理论最优值, 而IVMA算法在f 7, f 9两个测试函数中获取了理论最优值. 从整体函数测试结果来看, IVMA算法具有更好的收敛精度, 搜索能力优于其他对比算法.

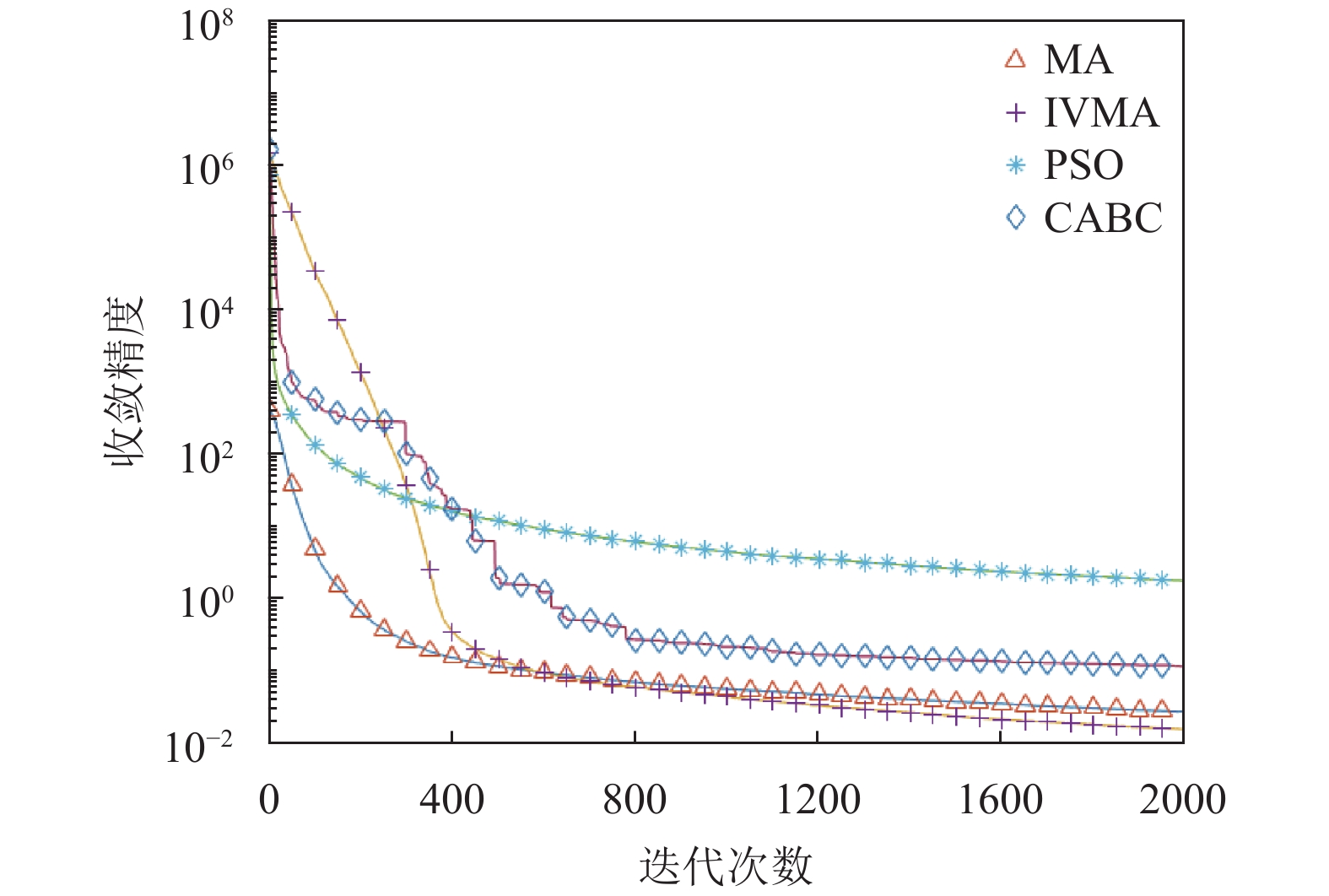
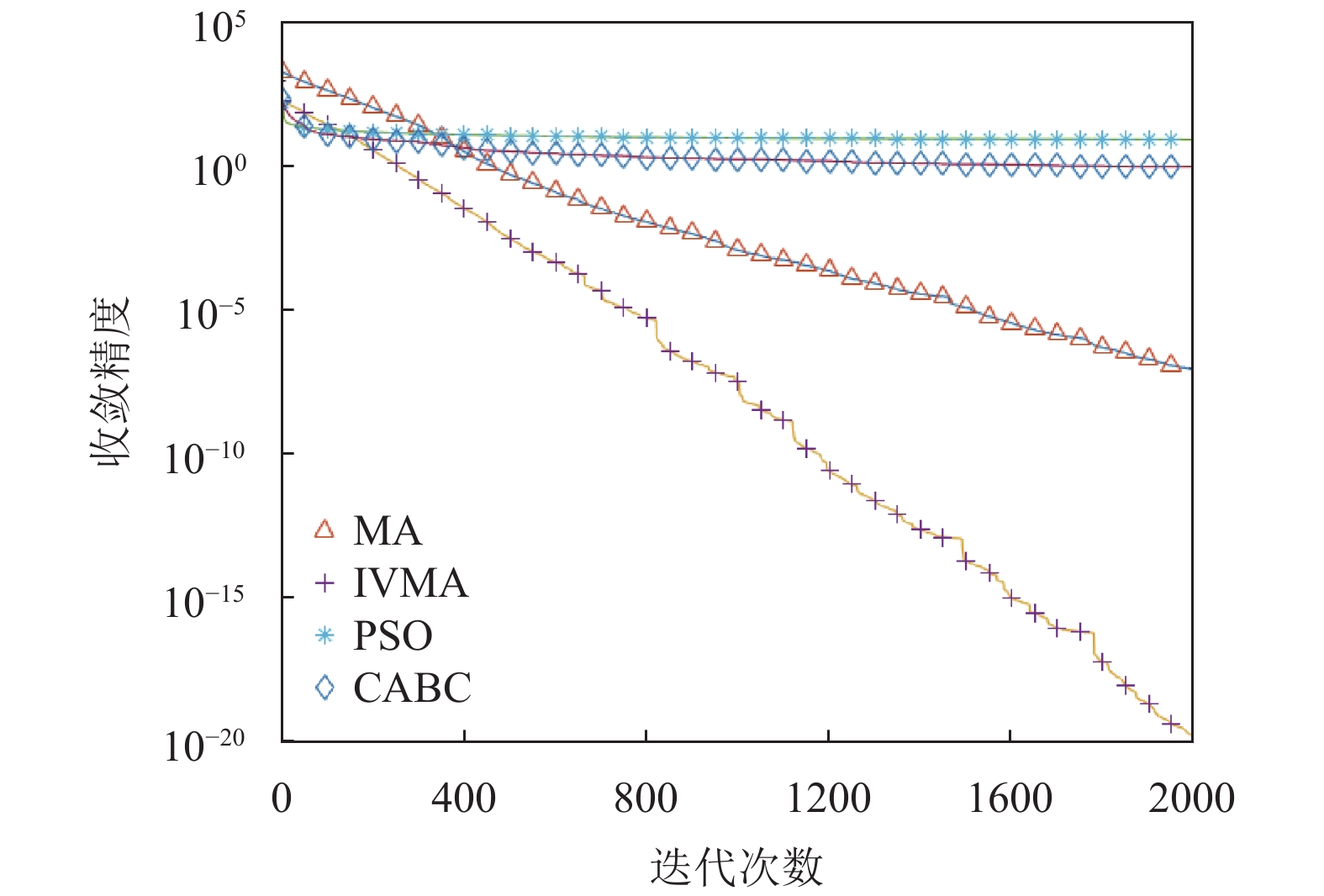
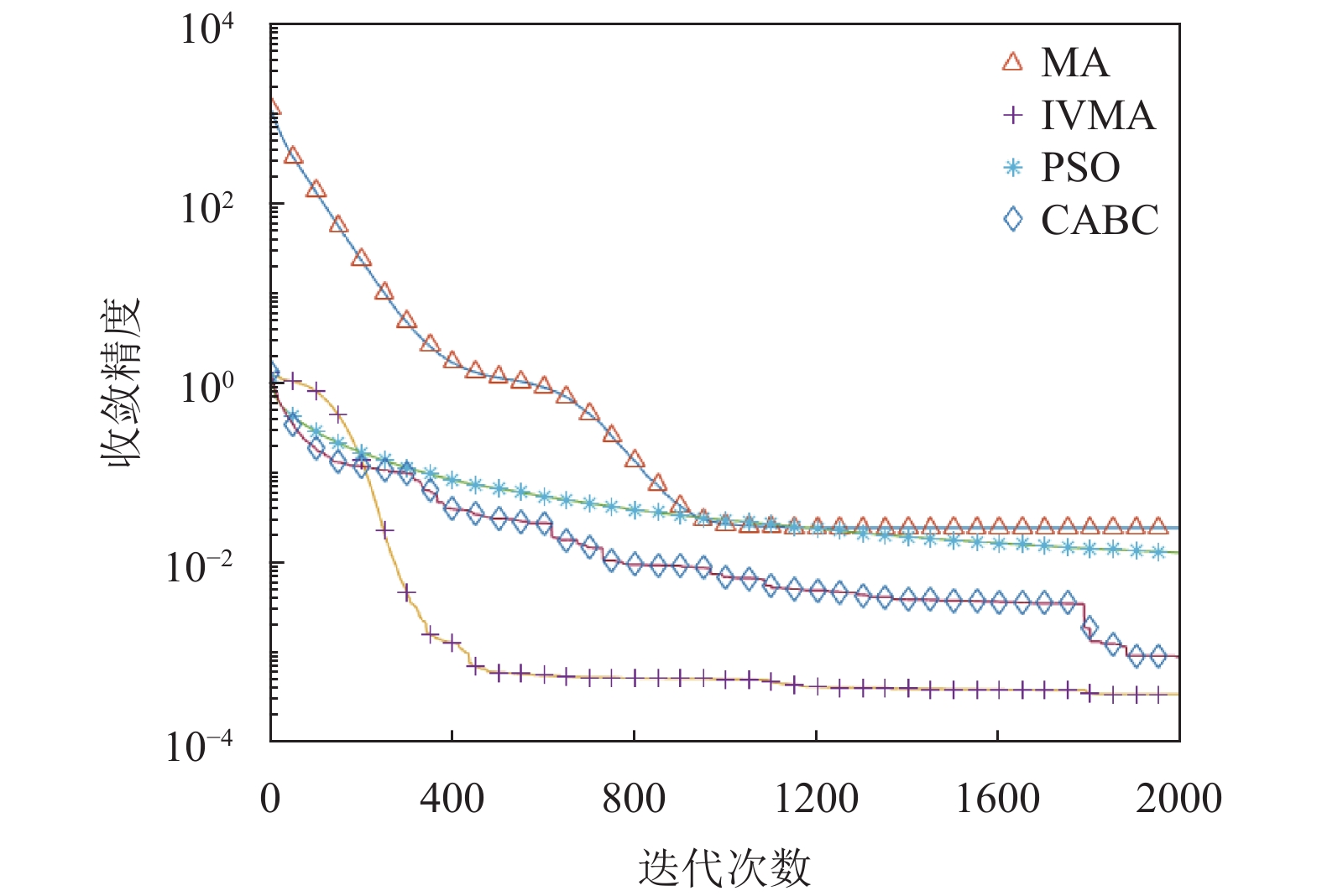
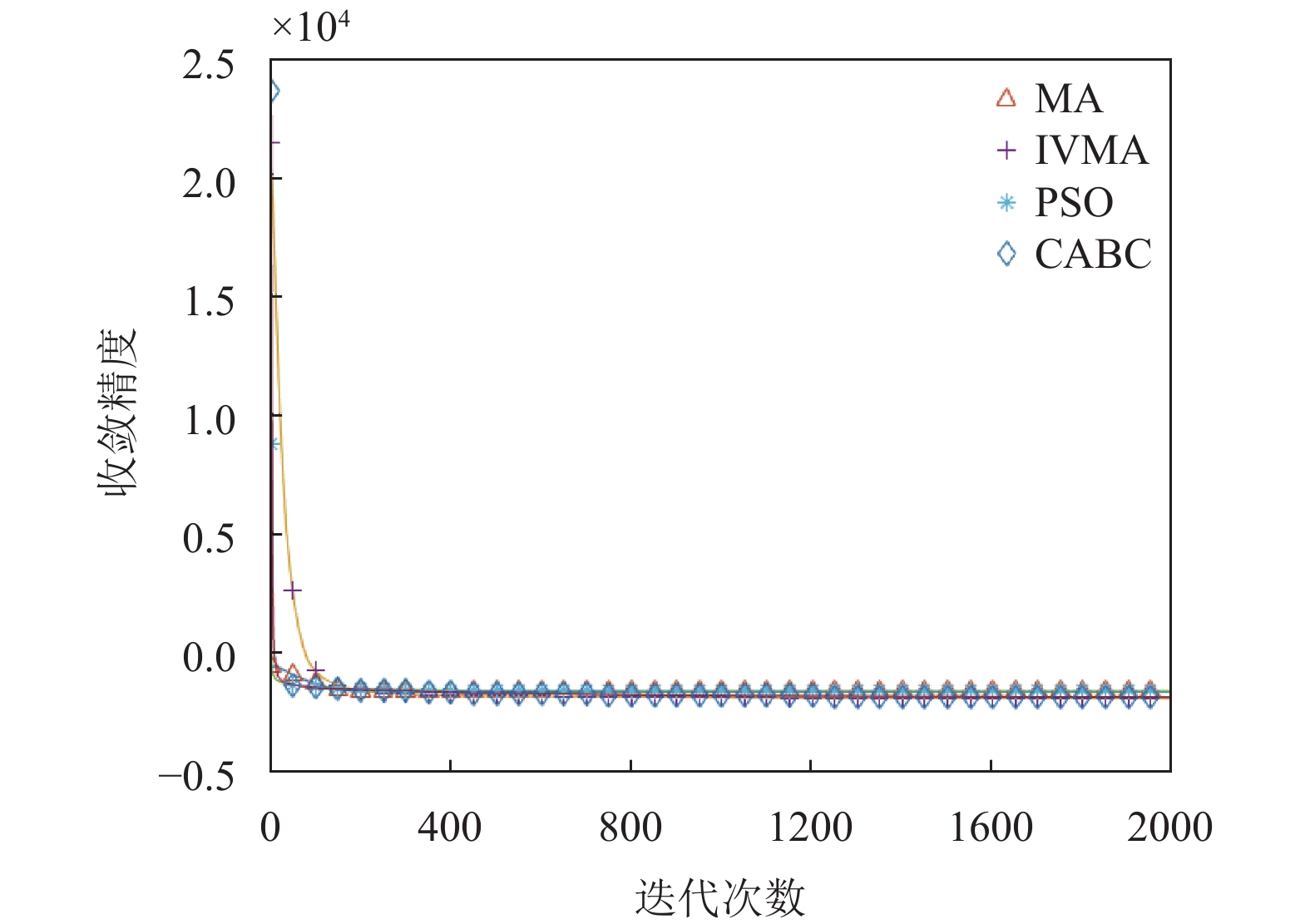
为了更直观地反应IVMA算法的搜索性能. 本文进一步绘制了IVMA算法, MA算法, CABC算法以及PSO算法的适应度收敛曲线图, 如图2~图11所示(其中横坐标为迭代次数, 纵坐标为收敛精度)

图 2 f1函数收敛性能比较

图 3 f2函数收敛性能比较

由函数图观察发现在f1, f2, f4函数中, MA算法相较于PSO算法和CABA算法具有一定优越性, IVMA提高了收敛精度. 函数f5中其他3种算法在迭代200次时都陷入了局部最优区域收敛趋于平缓, 但IVMA还是具有较好寻优能力. 函数f6中, MA算法, PSO算法, CABC算法的全局收敛性能并不好, 但IVMA经过倒位变异后, 改善了早熟收敛的问题, 提高了全局搜索的能力. 函数f7存在大量局部优值, MA算法在迭代至400次时, 陷入了局部最优, 但IVMA算法利用倒位变异保持了正确的搜索方向, 持续地寻找全局最优解. 函数f8中其他3种算法的收敛性能较差, 但IVMA算法从迭代开始至结束都具有良好的寻优能力, 在较少的迭代次数下获取了较好的优化结果. 在函数f7, f9中, IVMA算法较快的找到了全局最优, 算法性能得到极大提高.

图 4 f3函数收敛性能比较

图 5 f4函数收敛性能比较

图 6 f5函数收敛性能比较

图 7 f6函数收敛性能比较

图 8 f7函数收敛性能比较

图 9 f8函数收敛性能比较

4 结论

为了改善MA算法在高维复杂问题中全局收敛性能较差, 容易出现早熟收敛的问题. 本文提出了一种基于倒位变异的IVMA算法, IVMA算法引入倒位变异操作和改变MA算法在变异上的操作, 提高了跳出局部最优的能力. 对10个标准测试函数寻优的实验结果表明, MA算法相对于MA算, PSO算法和CABC算法, 在高维非线性复杂问题中具有更好的收敛精度, 优化了算法的寻优能力.

图 10 f9函数收敛性能比较

图 11 f10函数收敛性能比较

参考文献

[1]	刘利波, 周洁. 几种常规群体智能算法的研究进展. 电子技术与软件工程, 2016(3): 165.
[2]	楚东来, 赵伟辰, 林春城. 群智能算法的研究现状和发展趋势. 信息通信, 2015(11): 38-39. DOI:10.3969/j.issn.1673-1131.2015.11.019
[3]	Zervoudakis K, Tsafarak S. A mayfly optimization algorithm. Computers & Industrial Engineering, 2020, 145: 106559.
[4]	罗金炎. 融合随机逼近算法的粒子群优化算法. 计算机系统应用, 2015, 24(6): 108-113.
[5]	王东风, 孟丽. 粒子群优化算法的性能分析和参数选择. 自动化学报, 2016, 42(10): 1552-1561.
[6]	刘寒冰, 张亚娟. 求解0-1背包问题的改进混合遗传算法. 计算机系统应用, 2015, 24(6): 197-201.
[7]	张明, 张树群, 雷兆宜. 改进的萤火虫算法在神经网络中的应用. 计算机工程与应用, 2017, 53(5): 159-163. DOI:10.3778/j.issn.1002-8331.1508-0134
[8]	高卫峰, 刘三阳. 一种高效粒子群优化算法. 控制与决策, 2011, 26(8): 1158-1162.
[9]	夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法. 计算机学报, 2015, 38(7): 1397-1407. DOI:10.11897/SP.J.1016.2015.01397
[10]	罗钧, 李研. 具有混沌搜索策略的蜂群优化算法. 控制与决策, 2010, 25(12): 1913-1916.