近几年, 风电以成本较低、零污染等优势引起了各国高度重视, 得到了广泛应用风力发电量占比不断上升. 风力发电是通过捕捉大气中的气流产生的, 由于气流具有不确定性, 从而使得风力发电随机性和波动性明显, 这些特性增加了电网的调度难度[1]. 为了能更好地利用风力发电, 提高对风力发电能力的掌控, 风力发电功率精准预测至关重要.
风力发电预测的方法可以分为物理方法、统计学方法以及人工智能方法[2]. Landberg于1990年开发了基于物理方法的风力发电功率预测系统[3]. 该方法主要根据数字天气预报(NWP)对风力发电功率进行预测, 即根据气象预测值等推算出风电机组轮毂处的风速等信息, 根据模型得到风力发电功率预测. 另外, 在文献[4]中, 利用NWP和多个观测点的信息与特定风电场附近风机的位置进行了短期风电功率预测; 在文献[5]中, 提出了一种基于NWP网格数据优化的区域风电预测模型. 物理方法的优点在于不需要长期进行数据观测, 适用于新的风力发电场; 但该方法需要大量的计算, 同时还要考虑风速、风向以及其他信息, 导致建模困难, 在应用上有一定的局限性.
统计方法是根据已有风力发电功率的历史数据, 建立输入与输出之间的映射关系, 从而实现对风力发电功率的预测. 其中最常见的方法包括滑动平均法及其各种变形等. 在文献[6]中, 利用自回归滑动平均法(ARMA)模型进行了风速预测, 实验结果表明提前1小时进行风速预测的结果要好于提前4到9小时的预测结果. 在文献[7]中, 利用ARMA模型对风电场输出功率分别进行了短期和长期预测. 在文献[8]中, 将ARMA与支持向量机(SVM)结合, 得到了预测效果更好的风电预测模型. 与物理方法相比, 该方法不需要风向等信息, 仅需要风力发电功率的历史数据即可进行预测. 但统计风电功率数据具有自相关等特征, 导致预测误差会随着时间的增加而增加, 因此该方法不适用于长期预测.
相对于其它方法来说, 人工智能方法由于强大的机器学习能力, 在预测方面会取得更好结果. 常见方法有人工神经网络[9]、支持向量机[10]以及模糊逻辑[11]等. 在文献[12]中, 利用支持向量机回归(SVR)进行短期风电功率预测. 在文献[13]中, 采用最近邻支持向量回归(KNN-SVR)模型进行风电预测, 通过选取最接近点提高模型的预测精度. 在文献[14]中, 提出了一种基于自适应神经模糊推理系统(ANFIS)的风功率超短期预测方法. 在文献[15]中, 利用模糊C均值算法调整ANFIS的前件和后件参数, 提高了风电预测的精度. 与一型模糊系统相比, 二型模糊能更好地处理各类不确定性, 取得更好的建模与预测性能[16]. 但是由于经典二型模糊系统具有规则参数多、难优化等缺点, 需要相应方法进行规则约简以减少规则和参数规模, 并选择合理的参数优化方法进行参数的全局优化学习.
针对上述问题, 本文提出了一种基于差分进化和规则约简的二型模糊方法并应用到了风电预测. 本文的主要贡献为: (1)给出了一种二型模糊规则剪枝方法, 以期有效减少模糊规则数量和参数规模; (2)基于差分进化算法进行了约简二型模糊系统前后件参数的优化; (3)在风电预测中实现了成功应用, 并与一型模糊系统(ANFIS)和支持向量回归(SVR)方法进行了对比, 验证了所给方法的有效性和优越性.
1 基础知识本文提出的方法是基于二型模糊系统和差分进化算法的. 下面首先对相关知识进行简单介绍.
1.1 二型模糊系统1965年, Zadeh首先提出了模糊系统的概念, 模糊系统理论及其相关应用开始发展[17]. 1974年, Mamdan实现了用“IF-THEN”形式的模糊规则对蒸汽机进行控制[18]. 1992年, IEEE召开了关于模糊系统的国际会议, 并于下一年创办了专刊, 此后模糊理论得到了蓬勃发展. 此时的模糊系统主要是经典模糊系统, 也称为一型模糊系统. 为进一步提高模糊系统处理不确定性的能力, 获得更好的性能, 研究人员对一型模糊系统进行了扩展, 二型模糊系统应运而生. 二型模糊系统采用二型模糊集合, 从而有更高的自由度去处理各类不确定性, 取得更好建模、预测与控制性能[19-21], 并在很多领域得到了成功应用.
在论域X上的二型模糊集合
| $ \begin{array}{l} {\tilde A}={\int }_{x\in X}^{}\dfrac{{\mu }_{\tilde A}\left(x\right)}{x} ={\int }_{x\in X}^{}\dfrac{\left[{\int }_{u\in X}^{}\dfrac{{f}_{x}\left(x\right)}{u}\right]}{x}, {J}_{x}\subseteq \left[\mathrm{0, 1}\right] \end{array} $ | (1) |
其中,

|
图 1 高斯型二型模糊集合 |
本文中, 选择具有不确定标准偏差值的高斯型模糊集合
| $\left\{ {\begin{array}{*{20}{c}} {{{\overline \mu }_{\tilde A}}\left( x \right) = {\rm{exp}}\left[ { - \dfrac{1}{2}{{\left( {\dfrac{{x - m}}{{{\sigma _2}}}} \right)}^2}} \right]}\\ {{{\underline \mu}_{\tilde A}}\left( x \right) = {\rm{exp}}\left[ { - \dfrac{1}{2}{{\left( {\dfrac{{x - m}}{{{\sigma _1}}}} \right)}^2}} \right]} \end{array}} \right. $ | (2) |
假设所构建的模型具有n个输入变量
| $ \begin{split} \{R\left({i}_{1}, \cdots , {i}_{n}\right):\;& {\rm{if}}\;{x}_{1}\;{\rm{is}}\;{\tilde A}_{1}^{{i}_{1}}, \cdots , {x}_{n}\;is\;{\tilde A}_{n}^{{i}_{n}}, \\ &{\rm{then}}\;y\left(x\right)\;{\rm{is}}\; [{\underline w }^{{i}_{1}, \cdots , {i}_{n}}, {\overline{w}}^{{i}_{1}, \cdots , {i}_{n}}]\} \end{split} $ | (3) |
其中,
一旦将精确输入
| $ {F}^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right)=[{\underline f }^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right), {\overline{f}}^{{i}_{1}, \cdots , {i}_{n}}(\mathbf{x}\left)\right] $ | (4) |
其中,
采用降型与解模糊方法, 得到二型模糊模型的精确输出.
2 基于规则剪枝和差分进化算法的二型模糊方法本节首先给出基于规则剪枝和差分进化算法的二型模糊方法的整体流程, 然后分别探讨规则约简及参数优化策略.
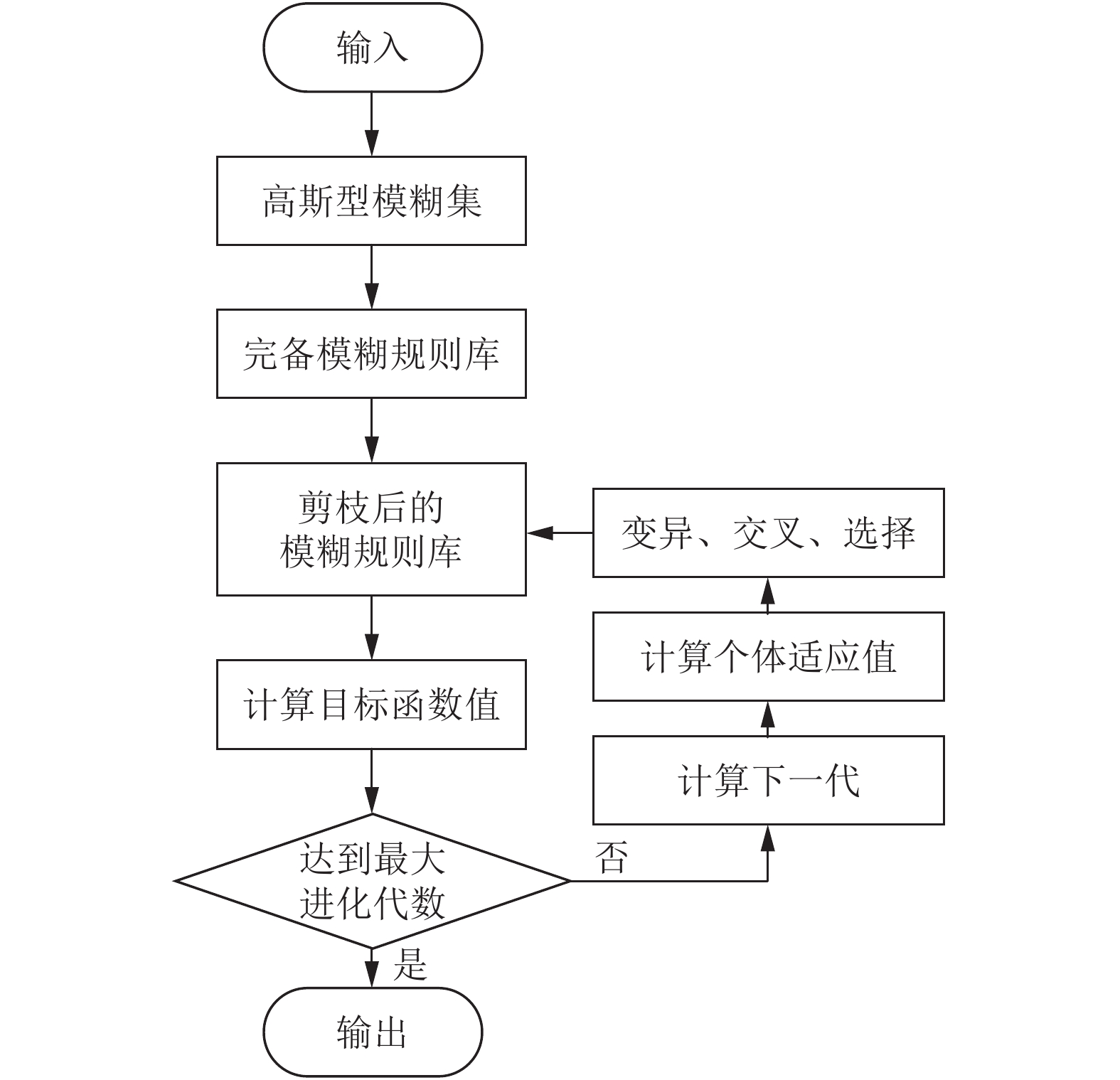
2.1 整体流程本文中约简二型模糊系统构建步骤如图2所示, 具体如下:
(1)根据训练数据集, 产生各输入变量的二型模糊划分, 生成完备的二型模糊规则库;
(2)通过训练数据得到的各规则的激活强度矩阵, 根据该矩阵实现二型模糊规则的剪枝;
(3)在约简后二型模糊规则库基础上, 采用差分进化优化对二型模糊规则的前后件参数进行优化;
(4)输出所得到的最终二型模糊预测模型.
下面各小节将具体探讨二型模糊规则的剪枝策略及约简后二型模糊系统的差分进化优化过程.
|
图 2 基于规则剪枝和差分进化算法的二型模糊方法整体流程图 |
2.2 完备二型模糊模型的规则剪枝
为了方便计算, 对于式(3)所示的完备二型模糊规则库, 其所代表的输入输出映射可以重写为:
| $\begin{split} {y}_{0}\left(\mathbf{x}\right)=&\alpha \frac{{\displaystyle\sum }_{{i}_{1}=1}^{{N}_{1}}\cdots {\displaystyle\sum }_{{i}_{n}=1}^{{N}_{n}}{\underline f }^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right){\underline w }^{{i}_{1}, \cdots , {i}_{n}}}{{\displaystyle\sum }_{{i}_{1}=1}^{{N}_{1}}\cdots {\displaystyle\sum }_{{i}_{n}=1}^{{N}_{n}}{\underline f }^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right)}\\ & +\left(1-\alpha \right)\frac{{\displaystyle\sum }_{{i}_{1}=1}^{{N}_{1}}\cdots {\displaystyle\sum }_{{i}_{n}=1}^{{N}_{n}}{\overline{f}}^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right){\overline{w}}^{{i}_{1}, \cdots , {i}_{n}}}{{\displaystyle\sum }_{{i}_{1}=1}^{{N}_{1}}\cdots {\displaystyle\sum }_{{i}_{n}=1}^{{N}_{n}}{\overline{f}}^{{i}_{1}, \cdots , {i}_{n}}\left(\mathbf{x}\right)} \\ =&\alpha \frac{\displaystyle\sum _{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}=1}}^{M}{\underline f }^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}\left(\mathbf{x}\right){\underline w }^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}}{\displaystyle\sum _{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}=1}}^{M}{\underline f }^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}\left(\mathbf{x}\right)}\\ & +(1-\alpha )\frac{\displaystyle\sum _{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}=1}}^{M}{\overline{f}}^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}\left(\mathbf{x}\right){\overline{w}}^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}}{\displaystyle\sum _{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}=1}}^{M}{\overline{f}}^{{k}_{{i}_{1}{i}_{2}{\cdots i}_{n}}}\left(\mathbf{x}\right)} \end{split}$ | (5) |
其中,
| $ \begin{split} {k_{{i_1}{i_2} \cdots {i_n}}} =& \left( {{i_n} - 1} \right) \cdot {N_1} \cdots {N_{n - 1}} + \left( {{i_{n - 1}} - 1} \right) \cdot {N_1} \cdots {N_{n - 2}} + \cdots \\ & + \left( {{i_2} - 1} \right) \cdot {N_1} + {i_1}. \end{split} $ |
为了简单起见, 将
| $ \begin{split} {y}_{0}\left(\mathbf{x}\right)=&\alpha \frac{\displaystyle\sum _{k=1}^{M}{\underline f }^{k}\left(\mathbf{x}\right){\underline w }^{k}}{\displaystyle\sum _{k=1}^{M}{\underline f }^{k}\left(\mathbf{x}\right)}+(1-\alpha )\frac{\displaystyle\sum _{k=1}^{M}{\overline{f}}^{k}\left(\mathbf{x}\right){\overline{w}}^{k}}{\displaystyle\sum _{k=1}^{M}{\overline{f}}^{k}\left(\mathbf{x}\right)}\\ =& \mathrm{\alpha }{\sum }_{k=1}^{M}{\underline {\gamma }}^{k}\left(\mathbf{x}\right){\underline w }^{k}+\left(1-\alpha \right){\sum }_{k=1}^{M}{\overline{\gamma }}^{k}\left(\mathbf{x}\right){\overline{w}}^{k} \end{split} $ | (6) |
其中,
首先, 计算训练数据
| $ {\mathbf{H}}_{0}={\left[\begin{array}{ccc}{\gamma }^{1}\left({x}^{1}\right)& \cdots & {\gamma }^{M}\left({x}^{1}\right)\\ ⋮& \ddots & ⋮\\ {\gamma }^{1}\left({x}^{N}\right)& \cdots & {\gamma }^{M}\left({x}^{N}\right)\end{array}\right]}_{N\times M} $ | (7) |
然后, 计算矩阵
| $ {\gamma }^{k}={\max}_{t=1}^{N}{\gamma }^{k}\left({x}^{t}\right) $ | (8) |
其中,
如果
通过规则剪枝, 二型模糊规则数量将会有效减少. 假定通过剪枝后剩余M'条二型模糊规则, 具体记为:
| $ \begin{split} &\left\{ {{R}^{k}:{\rm{if}}\;{x}_{1}\;{\rm{is}}\;{\tilde A}_{1}^{k}, {x}_{2}\;{\rm{is}}\;{\tilde A}_{2}^{k}, \cdots , {x}_{n}\;{\rm{is}}\;{\tilde A}_{n}^{k},} \right. \\ &\;\;\;\;\;\;\;\;\left. {{{\rm{then}}\;y\left(x\right)\;{\rm{is}}\;\left[{\underline w }^{k}, {\overline{w}}^{k}\right]}} \right\}_{k=1}^{{M}{{'}}} \end{split} $ | (9) |
其中,
如前所述, 在二型模糊规则库中, 模糊规则前件中的二型模糊集合可以通过直观划分得到. 但为获取良好性能, 如何进行二型模糊规则后件参数的优化仍待解决, 即, 二型模糊规则的区间权重
利用差分进化算法(Differential Evolution, DE)实现这些参数的优化学习. DE算法优化的具体步骤如下:
(1)初始化二型模糊系统的后件参数并定义目标函数;
(2)对得到的M'条二型模糊规则进行编号, 并根据目标函数计算相应的目标函数值;
(3)判断是否达到最大迭代次数, 如果达到则停止迭代进行下一步, 否则返回上一步;
(4)输出满足条件的最优值.
3 风电预测应用在这部分介绍了如何利用提出的风电预测模型进行实验.
3.1 实验数据文中选用2019年4月1日到2019年7月31日的风电数据进行训练和预测. 该数据来源于网站

|
图 3 原始风电数据图 |
3.2 对比模型
自适应模糊推理系统(ANFIS)将模糊逻辑和神经网络有机的结合在一起, 自动提取if-then规则, 并利用反向传播算法(BP)和最小二乘法进行前后件参数的调整以获取最优解, 既结合了两者的优点又弥补了两者的不足, 提高了模糊推理系统的学习能力.
支持向量回归(SVR)是支持向量机的一个重要应用分支. 该方法是将给定的训练样本数据映射到高位特征空间, 并在高维特征空间中进行线性回归, 并利用核函数代替内积运算, 降低了计算难度. SVR在样本数相对较少的情况下具有较强的泛化能力和良好的预测性能.
3.3 性能指标模型的性能指标用均方根误差(RMSE)、平均绝度误差(MAE)来衡量. RMSE是指预测值与真实值偏差的平方与个数n比值的平方根, 常常作为模型预测结果衡量的标准, RMSE越小则效果越好. MAE是指单个数据与算术平均值偏差的绝对值的平均值, 能很好的反映预测值误差的实际情况, 该值越小说明误差越小, 则预测效果越好. 公式表达如下:
| $ RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^{n}({y}^{i}-{p}^{i}{)}^{2}} $ | (10) |
| $ MAE=\frac{1}{n}\sum _{i=1}^{n}\left|{y}^{i}-{p}^{i}\right| $ | (11) |
其中,

|
图 4 预测结果 |
|
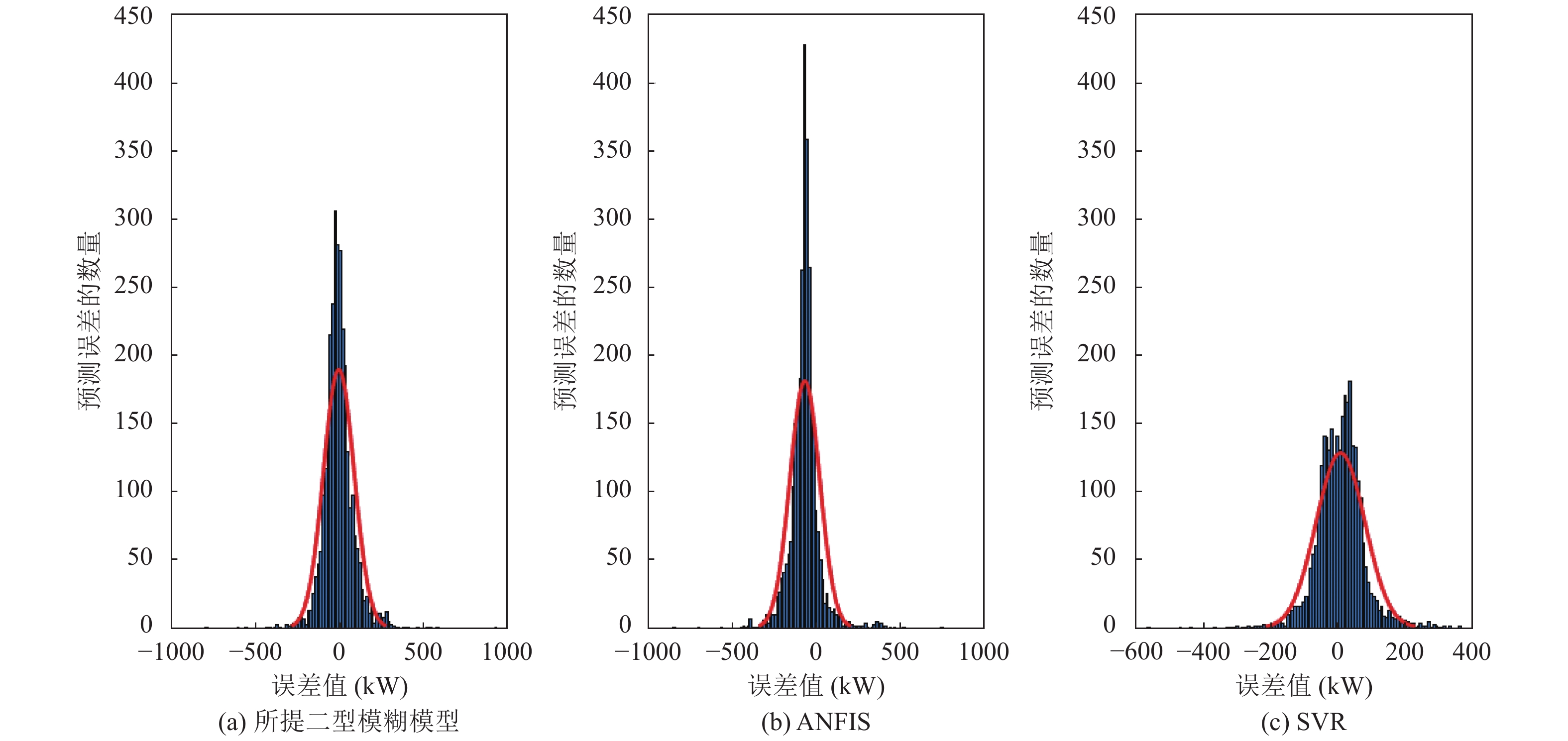
图 5 预测模型的误差直方图 |
文中所提的混合模型与其它风电预测模型的各指标对比如表1所示.
| 表 1 不同预测模型之间的指标对比 |
由图4的预测结果图可以看出, 二型模糊模型整体预测效果较好, 预测结果曲线与测试数据曲线拟合较好. 图5为预测误差直方图, 当分布在0附近的值越多时, 预测模型的性能越好. 从图5(a)中, 能清楚地看到所提模型的误差分布在0附近的较多, 图5(b)中的误差值在−100左右存在较多. 且对于误差直方图来说, 得到的曲线越高越窄, 则预测效果越好, 从图5中的误差直方图中看, 所提模型的预测效果要好于其他两个模型. 同时由表1中的性能指标对比结果可以看出, 无论是RMSE还是MAE指标, 所提混合模型的性能指标值均小于ANFIS和SVR的性能指标值. 通过性能指标对比来看, 对于RMSE和MAE这两个性能指标来说值越小则说明模型的性能越好, 因此可以得出文中提出的混合模型的性能要优于其它两个对比模型, 通过对不同模型进行组合确实能提高风电预测模型的性能.
4 结语针对二型模糊系统规则参数多、难优化等问题, 本文提出了一种基于差分进化和规则约简的二型模糊方法. 首先利用二型模糊规则剪枝方法减少模糊规则数, 然后利用差分算法对二型模糊系统的前后件参数进行优化. 并通过与ANFIS以及SVR两种模型进行对比证明该实验方法在风电预测方面表现良好, 验证了所提方法在风电预测方面的有效性.
| [1] |
Deng X, Shao HJ, Hu CL, et al. Wind power forecasting methods based on deep learning: A survey. Computer Modeling in Engineering & Sciences, 2020, 122(1): 273-301. |
| [2] |
Wang KJ, Qi XX, Liu HD, et al. Deep belief network based k-means cluster approach for short-term wind power forecasting
. Energy, 2018, 165: 840-852. DOI:10.1016/j.energy.2018.09.118 |
| [3] |
Foley AM, Leahy PG, Marvuglia A, et al. Current methods and advances in forecasting of wind power generation. Renewable Energy, 2012, 37(1): 1-8. DOI:10.1016/j.renene.2011.05.033 |
| [4] |
Khalid M, Savkin AV. A method for short-term wind power prediction with multiple observation points. IEEE Transactions on Power Systems, 2012, 27(2): 579-586. DOI:10.1109/TPWRS.2011.2160295 |
| [5] |
Wang Z, Wang WS, Wang B. Regional wind power forecasting model with NWP grid data optimized. Frontiers in Energy, 2017, 11(2): 175-183. DOI:10.1007/s11708-017-0471-9 |
| [6] |
Gomes P, Castro R. Wind speed and wind power forecasting using statistical models: AutoRegressive Moving Average (ARMA) and Artificial Neural Networks (ANN). International Journal of Sustainable Energy Development, 2012, 1(2): 41-50. DOI:10.20533/ijsed.2046.3707.2012.0007 |
| [7] |
惠小健, 王震, 张善文, 等. 基于ARMA的风电功率预测. 现代电子技术, 2016, 39(7): 145-148, 153. |
| [8] |
Wang YR, Wang DC, Tang Y. Clustered hybrid wind power prediction model based on ARMA, PSO-SVM, and clustering methods. IEEE Access, 2020, 8: 17071-17079. DOI:10.1109/ACCESS.2020.2968390 |
| [9] |
李军, 李大超. 基于优化核极限学习机的风电功率时间序列预测? 物理学报, 2016, 65(13): 130501.
|
| [10] |
Zeng JW, Qiao W. Short-term wind power prediction using a wavelet support vector machine. IEEE Transactions on Sustainable Energy, 2012, 3(2): 255-264. DOI:10.1109/TSTE.2011.2180029 |
| [11] |
Jiao RH, Huang XJ, Ma XH, et al. A model combining stacked auto encoder and back propagation algorithm for short-term wind power forecasting. IEEE Access, 2018, 6: 17851-17858. DOI:10.1109/ACCESS.2018.2818108 |
| [12] |
王宁, 叶林, 陈盛, 等. 支持向量机向量维数对短期风电功率预测精度的影响. 电力系统保护与控制, 2012, 40(15): 63-69. DOI:10.7667/j.issn.1674-3415.2012.15.012 |
| [13] |
徐正华, 刘三明, 王致杰. 基于kNN-SVR模型的风电功率预测. 电力学报, 2019, 34(5): 411-416. |
| [14] |
王艳艳, 尹少平, 王灵梅, 等. 基于ANFIS模型的风功率超短期预测研究. 自动化技术与应用, 2016, 35(1): 17-21. |
| [15] |
高骞, 程霄, 沙宇恒, 等. 基于ANFIS的超短期风电出力预测模型及仿真. 沈阳工业大学学报, 2020, 42(1): 29-33. DOI:10.7688/j.issn.1000-1646.2020.01.06 |
| [16] |
李军, 王星辉. 基于区间二型FLS的短期风电功率多步预测. 控制工程, 2019, 26(2): 215-222. |
| [17] |
Zadeh LA. Fuzzy sets. Information and Control, 1965, 8: 338-353. DOI:10.1016/S0019-9958(65)90241-X |
| [18] |
Mamdani EH. Application of fuzzy algorithms for control of simple dynamic plant. Proceedings of the Institution of Electrical Engineers, 1974, 121(12): 1585-1588. DOI:10.1049/piee.1974.0328 |
| [19] |
Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning-I. Information Sciences, 1975, 8(3): 199-249. DOI:10.1016/0020-0255(75)90036-5 |
| [20] |
Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning-II. Information Sciences, 1975, 8(4): 301-357. DOI:10.1016/0020-0255(75)90046-8 |
| [21] |
Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning-III. Information Sciences, 1975, 9(1): 43-80. DOI:10.1016/0020-0255(75)90017-1 |
| [22] |
Mendel JM. Uncertain rule-based fuzzy logic systems: Introduction and new directions. Upper Saddle River, NJ: Prentice Hall PTR, 2001.
|
 2021, Vol. 30
2021, Vol. 30



