随着物联网与各种通信技术的快速发展, 无线传感网络(Wireless Sensor Network, WSN)开始受到广泛关注^[1]. WSN作为信息采集的一种重要手段, 相比于传统有线或者人工信息采集优势十分明显, WSN可以做到快速部署以及大规模覆盖, 因此WSN目前广泛应用于军事、工业、农业等多个领域^[2]. 然而传感器的寿命完全依赖于电池^[3], 如果由传感器因为电池耗尽而停止工作, 那么无线传感网络的信息采集完整度就会受到很大的影响. 因此降低WSN的能耗, 同时保证网络传输质量是一个值得研究的问题.

本文提出了一种适用于密集分布无线传感器网络的数据聚合方案, 首先利用网格聚类划分网络, 然后通过模糊强化学习选取数据聚合节点并利用果蝇优化算法动态定位外部通信节点降低了无线传感网络的能耗, 同时也保证了较低的丢包率和端到端延迟.

1 研究现状

目前关于无线传感网络国内外已有大量相关学者进行了深入研究. 文献[4]针对节点覆盖不均匀的问题, 提出了一种自适应粒子群优化算法. 文献[5]提出了一种利用压缩感知(HDACS)进行分层数据聚合的方法, 根据集群的大小, 建立多个压缩阈值; 在不同级别的数据收集中, 传输的信息量被优化. 文献[6]提出了一种基于模糊逻辑的多层协议, 以提高分布式WSN中数据聚合的处理效率. 文献[7]提出了一种基于代理的服务器系统方法, 该方法改善了IoT/CPS提供程序中异构WSN之间的资源共享. 上述的一些研究内容中大多没有考虑数据聚合过程中可能存在的一些问题, 在WSN应用中, 经常产生大量的冗余感知数据使得数据聚合更加耗能^[8,9]. 为了降低能耗, 在文献[10,11]中采用了一种有效的数据聚合技术来控制数据, 根据网络拓扑、网络流和服务质量对数据聚合过程进行分类. 文献[12]将从不同传感器节点获得的数据合并后进行冗余消除, 以减少向汇聚节点的数据传输次数. 此外还有如EASR (Energy Aware Sink Relocation) ^[13]、TCBDGA (Tree-Cluster-Based Data-Gathering Algorithm)^[14]和FR-EEDG (Fuzzy Reinforcement learning-based Energy-Efficient Data Gathering)^[15]等一些数据聚合方案, 然而这些方案的问题是数据的聚合依赖于簇头和汇聚节点, 当网络大小和节点密度增加时, 它会自动最大化能量的利用, 从而导致网络的生命周期变短. 因此为了解决上述问题, 本文提出了一种适用于密集分布无线传感器网络的节能数据聚合方案.

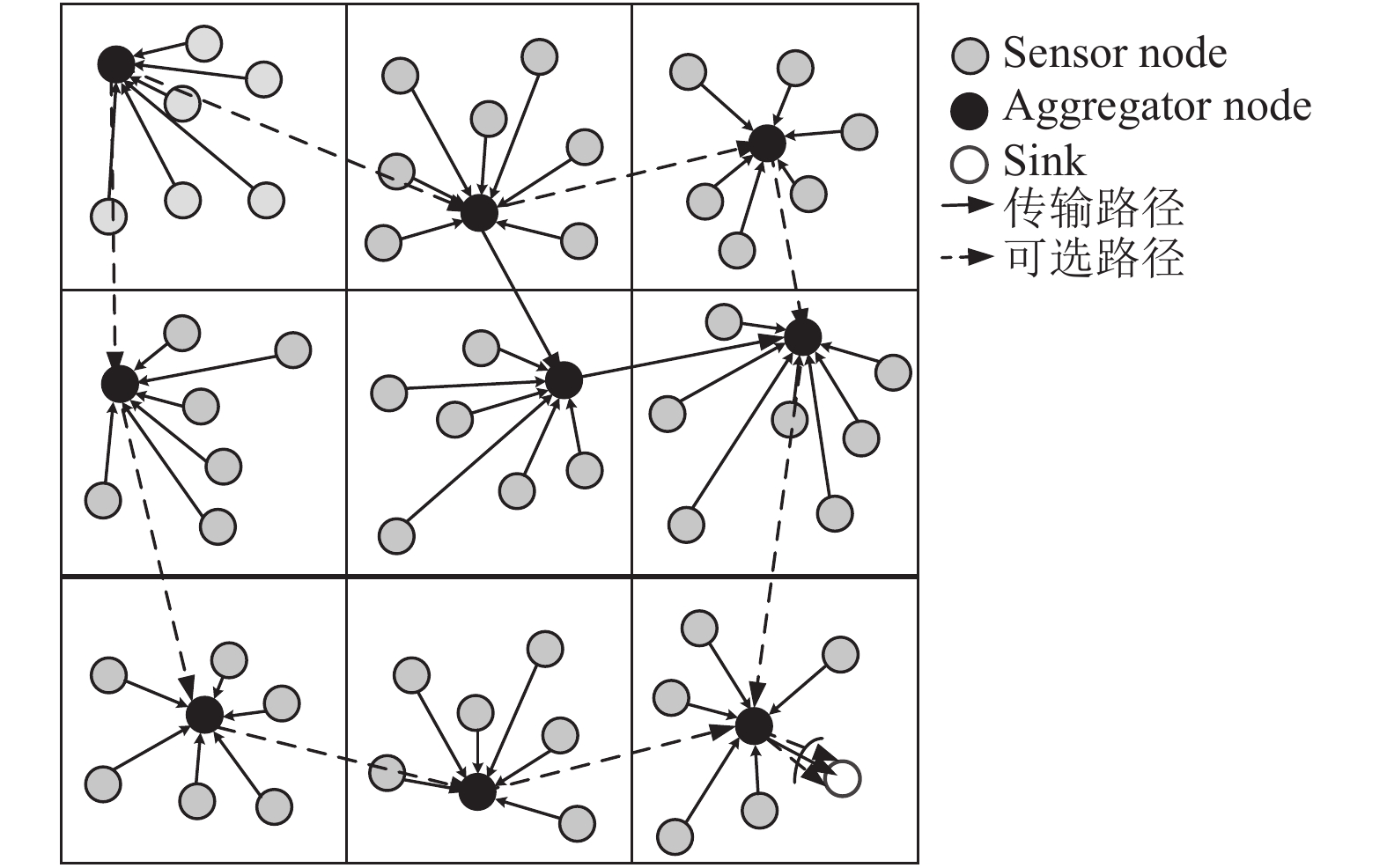
2 系统模型 2.1 网络节点模型

本文网络节点模型如图1所示, 将传感器网络区域的整个区域划分成网格单元簇, 再将网格单元中的所有可用节点中用树形结构连接, 并选择一个簇头进行外部数据传输. 图中的每个节点都满足如下两个条件:

(1)网络中的所有节点都有类似的配置.

(2)接收和网络中所有其他考虑的节点都是静态的, 在部署之后, 它不能移动到网络的任何地方.

其中, sensor nodes为传感器节点, aggregator node为一个网格簇的数据汇聚节点, sink为整个传感器网络的数据汇聚节点和外部通信节点(可为网络中的任意节点), 为了加以区分, 下文中的相关节点都将用英文表示.

2.1.1 网格划分

要将传感器网络划分成图1所示的网格结构, 需要执行下面两个步骤:

步骤1. 对网络区域进行纵向划分, 将其划分为高为H, 宽为W的矩形区域, 用1~n对这些矩形的进行编号.

步骤2. 将每个矩形划分成更小且不相等的区域, 即网格. 每个的位置与数据汇聚点之间的距离决定了在这个矩形中创建的网格的边界. 我们用 $(m,n)$ 表示第 $n$ 个矩形中的第 $m$ 个网格, 则网格 $(m,n)$ 的边界可以由式(1)求出:

$ \left\{ \begin{split} & (c - 1) \times W < m \le c \times W \\ & \sum\nolimits_{l = 0}^{q - 1} {{h_{cl}} < v \le } \sum\nolimits_{l = 0}^q {{h_{cl}};\;l = 1,\cdots,j;\;q = 1,\cdots,k} \\ \end{split} \right. $

(1)

其中, l和c用于表示网格线以及网格的列向量, h_cl表示网格高度. 令第i个节点的坐标为(a,b), 那么在网格划分结束后就可以得到节点所属于的网格.

2.1.2 网格聚类和簇头选择

在每个网格单元中, 聚类和簇头选择过程由sink节点启动. Sink节点会定期将信标消息发送到sensor节点, sensor节点会发送包含位置信息和能级信息的回复消息. 从sensor节点获得此信息后, sink节点根据最大剩余能量水平因数选择簇头. 表1显示了传感器节点的详细信息.

CH (Cluster Header)表示簇头, k(i,sink)表示sink节点与第i个sensor节点之间的长度. 式(2)用于判断传感器节点能否作为簇头:

$ {O}_{\rm CH}= {\left(\dfrac{{max}ID-I{D}_{i}}{{max}ID}\right)}^{{c}_{1}}\times {\left(\dfrac{{E}_{{\rm{cur}}}}{{E}_{{\rm{ini}}}}\right)}^{{c}_{2}} $

(2)

其中, maxID表示为网络中存在的节点的最大ID, E_cur表示节点i的当前能量, E_ini表示初始能量, c₁和c₂表示为从0到1的任意常数范围.

2.2 基于模糊规则系统评估aggregator节点

Aggregator节点的选择是在网格簇的簇头节点帮助下进行的. 模糊规则系统将簇头距离(Cluster Header DIStance, CH_DIS), 邻域重叠(Neighbourhood OVERlap, NOVER)和代数连通性(Algebraic Connectivity, AC)视为解决aggregator节点适用性的3个指标.

NOVER为直接度量, 用于确定两个节点的链路之间存在的已连接邻居的范围, 具有最高NOVER值的节点链路的起始节点最有可能成为簇头节点. 节点链接的AC用于评估节点到节点链接连接的鲁棒性, 较高AC值的节点链接也更有可能成为簇头节点. 模糊逻辑系统根据三角隶属函数公式为输入指标找到相关的隶属函数.

模糊化步骤: 在此步骤中, 模糊器调用数据输入指标的清晰值, 并提供给它们相对预定义的隶属度函数以及模糊描述变量.

映射步骤: 基于表2中列出的知识库规则库, 推理机根据CH_DIS, NOVE和AC的模糊值, 将其映射到预定义的规则, 以获取成为aggregator节点的等级, 作为模糊输出值. 例如CH_DIS值为near, NOVER值为good, AC值为strong, 则节点等级为acceptable.

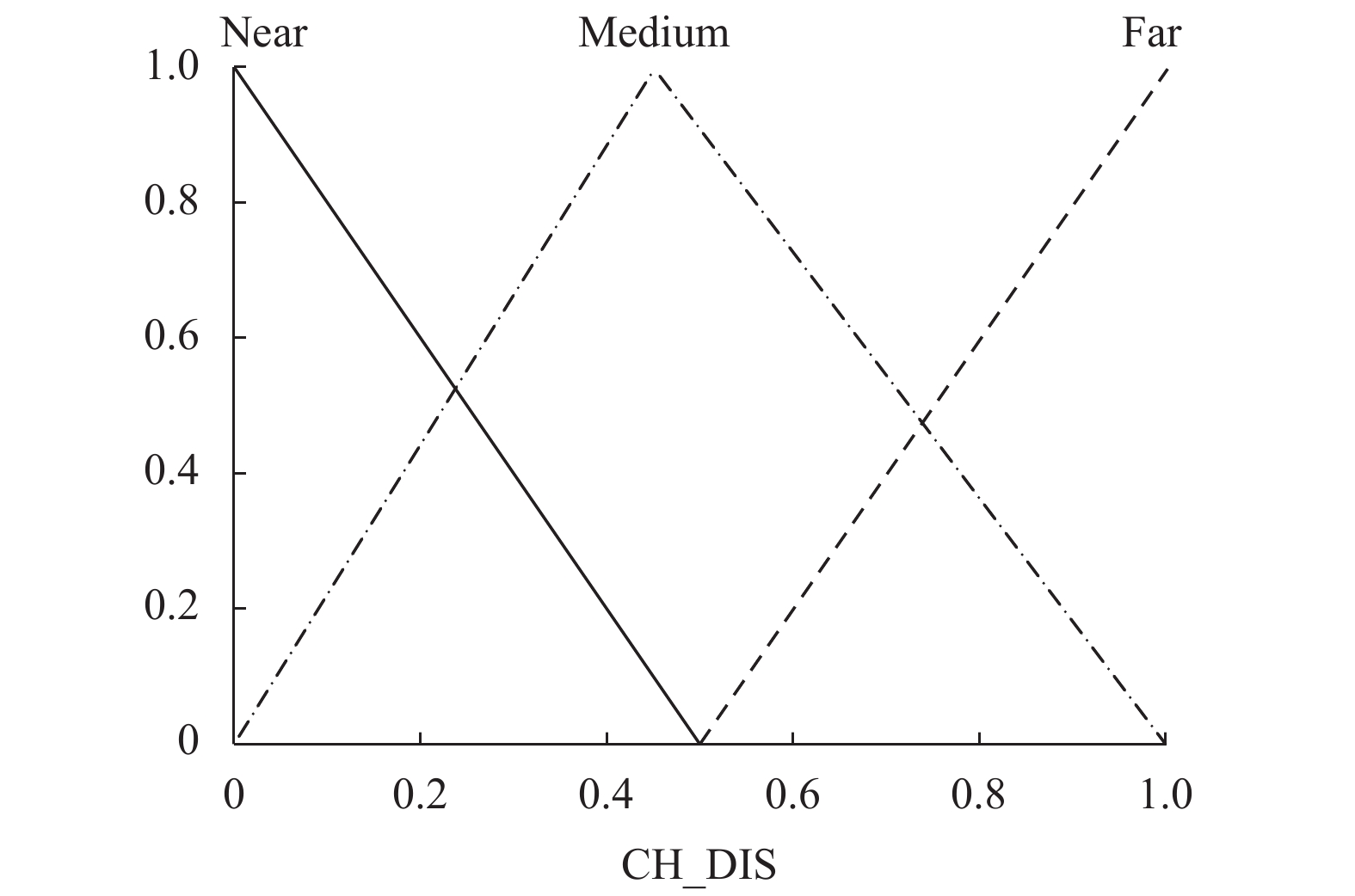
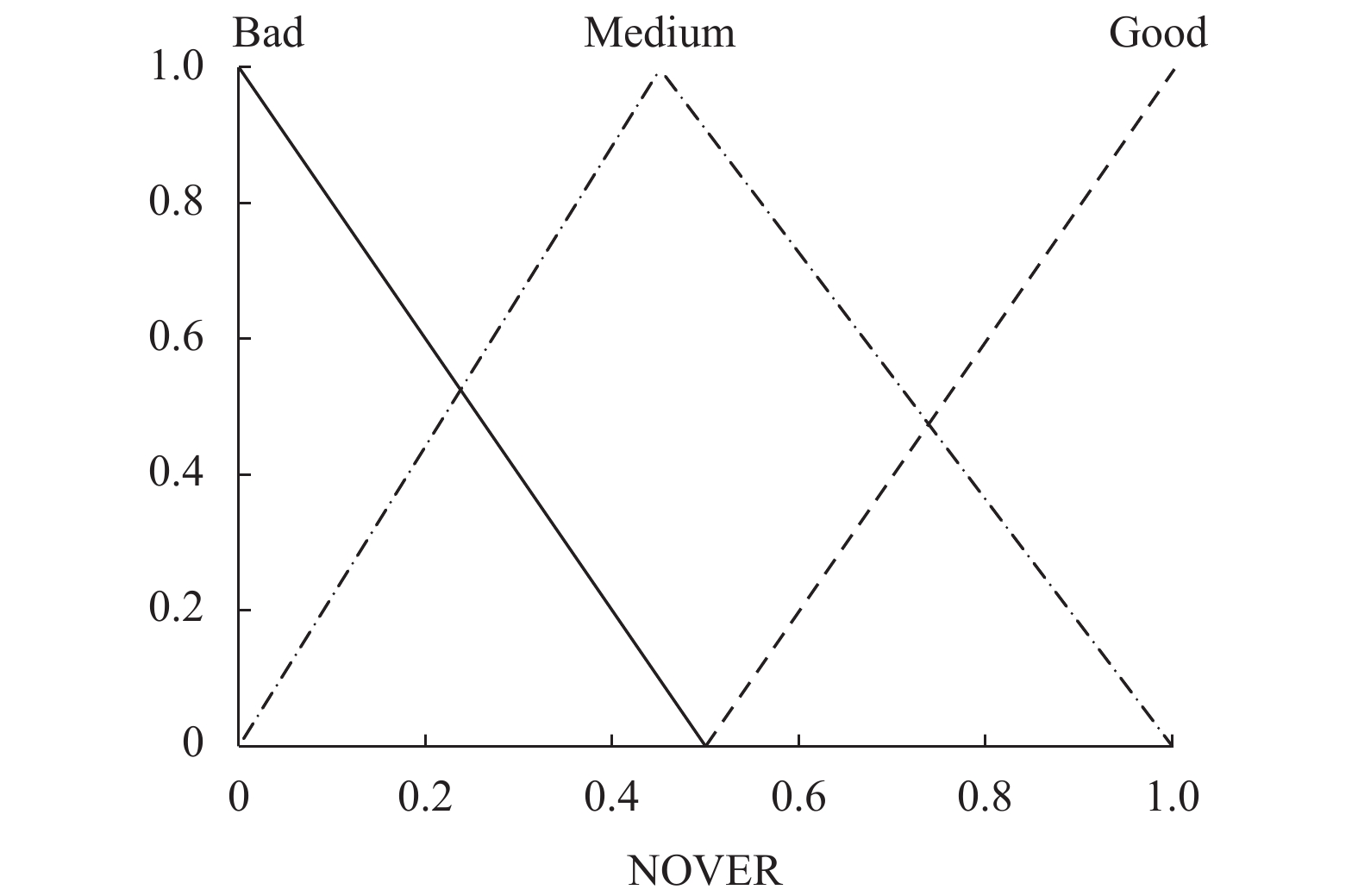
去模糊化: 在去模糊化过程中, 使用预定义的输出隶属度函数将模糊输出值转换为相关的数值. CH_DIS, NOVER和AC的隶属函数如图2~图4所示.

重心法用于去模糊化. 其数学定义为:

$ {x_{{\rm{COG}}}} = \frac{{\int x {\mu _A}(x){\rm{d}}x}}{{\int {{\mu _A}} (x){\rm{d}}x}} $

(3)

其中, A表示模糊集, x是样本元素, 而 $\;{\mu _A}(x)$ 是模糊集的隶属函数. 最终的去模糊值是对应于图5中所示顶点的x坐标值, 它定义了节点的能力值.

2.3 基于模糊强化学习选取aggregator节点

整个网络被表示为一个环境, 所有集群成员节点都参与学习. 通过交换信标消息, 每个节点与其他节点一起学习整个网络环境. 选择根节点是每个节点上用于数据传输和聚合的操作. 每个节点都有一张Q表, 其中每个Q值(Q(s_t, r))表示在状态s_t处选择r作为根节点的值.

对于每个动作和状态, 每个节点都必须维持Q值. 其中, 状态是当前节点的链路质量. 动作是将当前节点选作根节点, 以达到与相邻节点的最大链路质量. Q表以5 s的间隔频繁更新. 从接收器节点接收到信标消息后, 未选择节点的Q表将更新. 每个节点的Q值在开始时都设置为0. 从接收器接收到信标消息后, 初始节点将与接收器对应的Q值更新为:

$ \begin{split} & {Q_b}\left( {{s_t},r} \right) \leftarrow \lambda \times BQ(r,b) \times \left\{ {R + \mu \times \mathop {\max }\limits_{\mu \in {N_r}} \left( {{s_t} + 1,\mu } \right)} \right\} \\ & \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{} \end{array} + (1 - \lambda ) \times {Q_b}\left( {{s_t},r} \right) \\ \end{split} $

(4)

其中, BQ(r,b)是信标消息的接收率. 对于Q_b(s_t,r), 箭头左边表示当前值, 右边表示先前值, N_r代表群集内节点的数量. 当前状态和下一个状态分别表示为s_t和s_t+1.

学习率( $\lambda $ )为0.6, 折扣系数( $\;\mu $ )为0.8. $\mathop {\max }\limits_{\mu \in {N_r}} \left( {{s_t} + 1,\mu } \right)$ 是成为根节点的节点r的最大Q值, 奖励R为:

$ R=\left\{ {\begin{array}{*{20}{l}}\mathrm{max}\left(\dfrac{L{Q}_{r}}{L{Q}_{1r}\times \left|{N}_{C}\right|},1\right),& b\in {N}_{C}\\ 0,& {\text{其他}}\end{array}} \right. $

(5)

其中, LQ_r是计算得出的当前节点到邻居节点的链路质量, 而LQ_1r是节点1可获得的最大链路质量. N_c表示特定群集中可用的活动节点集. 如果节点r达到良好的链路质量, 则奖励为正; 否则, 奖励为0. 对于整个网络, 经过不断的强化学习, 最终每个节点都维护了一个学习随迭代次数波动较小的Q矩阵, Q矩阵给出了在不同状态下应该选定作为根节点的aggregator节点.

2.4 基于FOA的sink节点迁移机制

果蝇优化算法(Fruit fly Optimization Algorithm, FOA)的主要目标是根据sink节点的先前坐标执行重定位操作, 并且与其他优化算法相比, FOA可以实现更好的收敛速度. 在本文中, FOA遵循基于气味的搜索机制. 考虑两个部分. 第一阶段是确定sink节点重定位的条件, 第二阶段是确定sink节点移动的路径和重定位距离. 重新定位的过程在算法1中进行了描述.

算法1. 基于FOA的sink节点迁移

输入: V (传感器节点集合); N (每个节点的邻居节点集合); B (sink节点的初始位置); r(u) (簇头u剩余能量)

While true

1. $\scriptstyle \forall u \in V$ , 收集剩余的能量 $\scriptstyle r(u)$ ;

2. 在每个传感器节点中, 通过对传输范围的调整, 确定WSN的通信图G;

3. $\scriptstyle \forall u \in V$ , 计算极限能力路径 $\scriptstyle P_{us}^*$ 和极限能力值 $\scriptstyle {{C}}\left( {P_{us}^*} \right)$ ;

4. 定义上下左右4个可移动的方向, 一次可以移动的距离为20:

左移: $\scriptstyle \left\{ {\begin{array}{*{20}{c}} \scriptstyle{X_i}={{X}}_{\rm{axis}}-20 \\ \scriptstyle{Y_i}={{Y}}_{\rm{axis}}+0 \end{array}} \right.$

右移: $\scriptstyle \left\{ {\begin{array}{*{20}{c}} \scriptstyle{X_i}={{X}}_{\rm{axis}}+20 \\ \scriptstyle{Y_i}={{Y}}_{\rm{axis}}+0 \end{array}} \right.$

上移: $\scriptstyle \left\{ {\begin{array}{*{20}{c}} \scriptstyle{X_i}={{X}}_{\rm{axis}}+0 \\ \scriptstyle{Y_i}={{Y}}_{\rm{axis}}+20 \end{array}} \right.$

下移: $\scriptstyle \left\{ {\begin{array}{*{20}{c}} \scriptstyle{X_i}={{X}}_{\rm{axis}}+0 \\ \scriptstyle{Y_i}={{Y}}_{\rm{axis}}-20 \end{array}} \right.$

5. 计算新坐标所在网格簇的所有节点到所有aggregator节点的跳数, 作为算法中的味道浓度值, 跳数越短, 浓度值越大;

6. 将每个网格簇中总跳数最短的节点标记为可行点, 4个节点的权值标记为w₁, w₂, w₃, w₄, 迁移路径为可行路径;

7. 设 $\scriptstyle{S_{C_i^*}}$ 为 $\scriptstyle{w_1},{w_2},{w_3}{\rm{ ,}}{w_4}$ 中权值最大的移动候选节点;

8. If $\scriptstyle{S_{C_i^*}}$ 节点的味道浓度值小于当前sink节点;

Break;

Else 将sink节点重定位到 $\scriptstyle S_{C_i^*}$ ;

End if

End while

3 仿真及结果分析

本文仿真在Matlab中进行, 分别对本文所提方案的丢包率, 端到端时延以及能量消耗做出了仿真, 仿真参数如表3所示.

3.1 丢包率

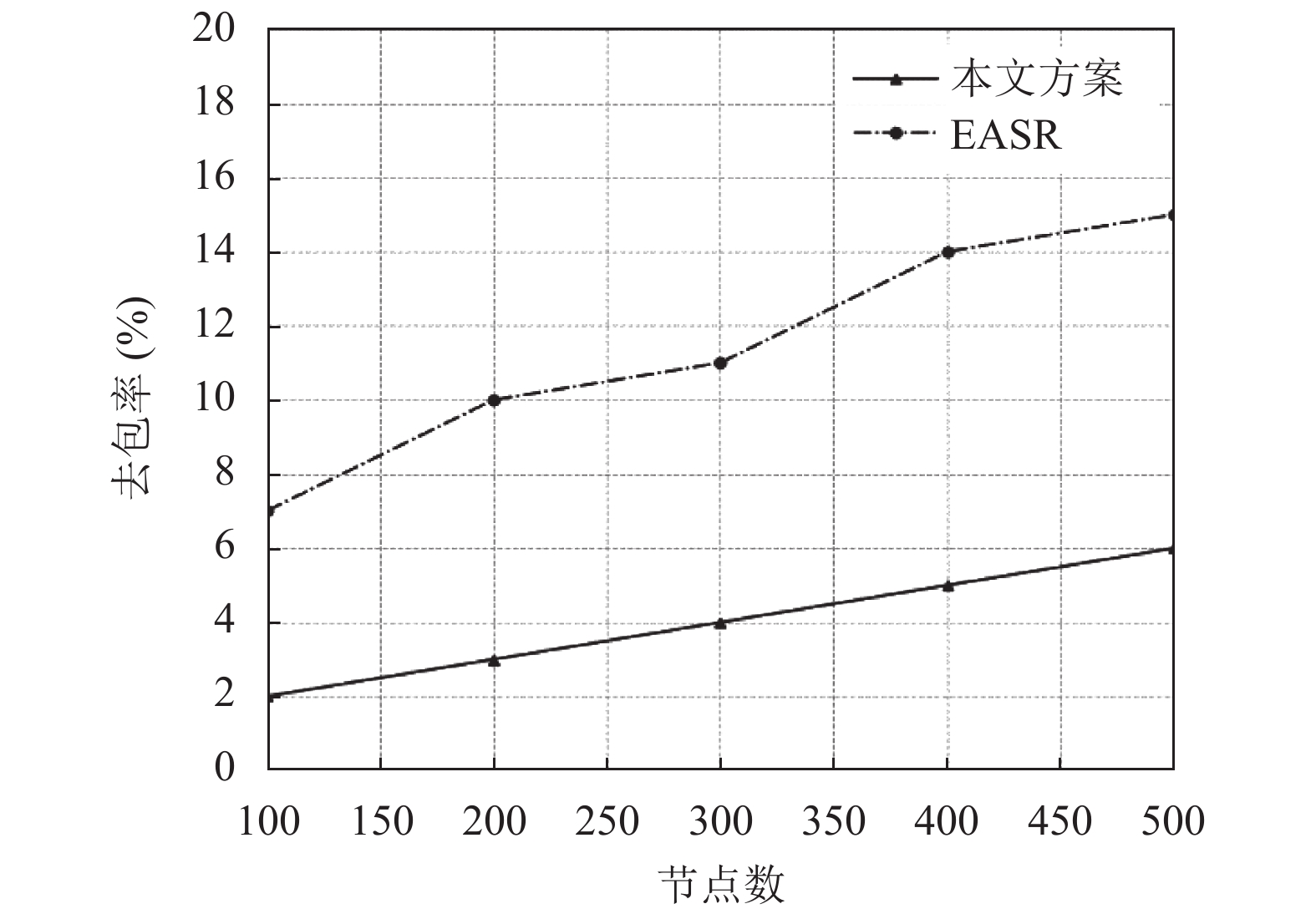
丢包率(Packet Loss Ratio, PLR)定义为从源到目标节点的传输以及在目标节点中接收时发生的数据丢失, 是传输的数据与接收的数据之比, 以100个节点为单位, 如式(6)所示:

$ {{PLR}} = 100 - \frac{{{{dat}}{{{a}}_{{\rm{transmit}}}}}}{{{{dat}}{{{a}}_{{\rm\rm{receive}}}}}} \times 100 $

(6)

图6为节点数和PLR的关系, 本文所提方案相比EASR的丢包率始终保持在较低水平. 因为每个aggregator节点仅覆盖有限的范围, 并且在网格聚类时根据节点的距离进行调整, 从而避免了重叠, 节点被放置在彼此的半径内, 这导致分组丢失最小化.

3.2 端到端延迟

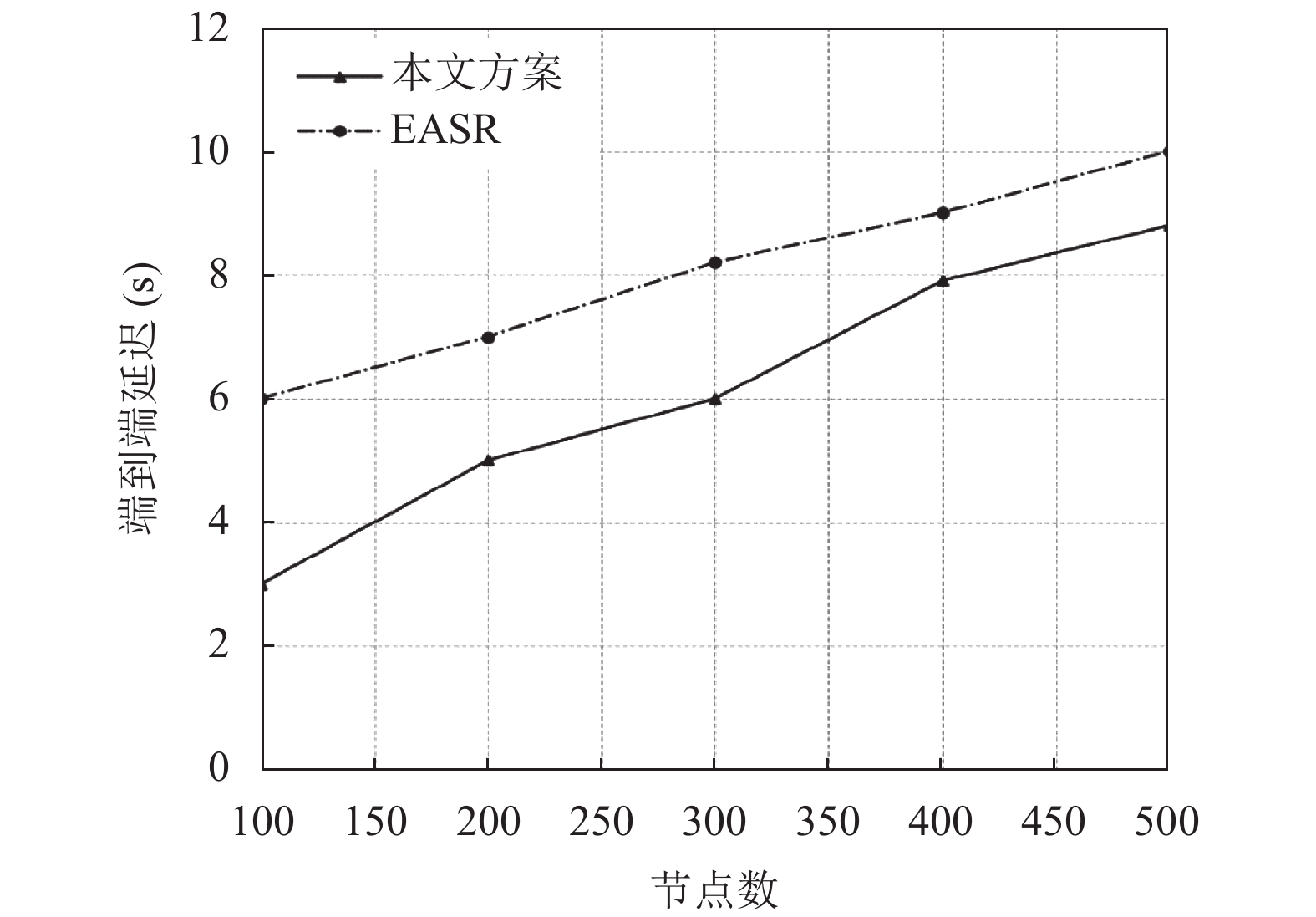
端到端延迟由式(7)计算得出:

$ {{d = }}{{{t}}_{{\rm{recive}}}}{{ + }}{{{t}}_{{\rm{transmit}}}} $

(7)

端到端延迟的评估如图7所示. 提出的系统比其他现有系统具有最低的延迟. 在100个节点中, 所提出方案的端到端延迟为2.8 s, 而EASR为6 s.

3.3 能量消耗

WSN中节点能耗影响数据的传输以及网络效率, 因此, 它成为至关重要的问题. 令E_con是节点固定能耗, l²为能量损失率, 群集节点之间的跨度用d表示. 数据通过放大器传输到节点的能耗为 ${{{t}}_{{\rm{amp}}}} \times {l^{\rm{2}}}$ , 其中t_amp是用于传输数据的能量. m表示数据长度(位). 然后通过以下公式计算能量:

$ {{{E}}_{{{tx}}}}({{m}},{{d}}){\rm{ = }}{{{E}}_{{\rm{con}}}} \times {{m + }}{{{t}}_{{\rm{amp}}}} \times {{m}} \times {l^{{2}}} $

(8)

在图8中, 仿真显示了能耗评估. 通过与EASR进行比较, 本文方案的能耗显著降低, 在100节点时, 本文方案使用50 MJ的能量, 而EASR系统使用150 MJ的能量.

在所提出的方案中, 通过sink节点重定位避免了数据聚合的复杂性. 因此, 防止了重复的数据传输. 当两个节点位于彼此的半径内时, 冗余数据可能会转发到aggregator节点, 这会最大化aggregator节点的工作负载, 并且浪费能源. 因此, 通过避免重复数据, 处理操作被最小化, 并且聚合器节点的寿命得以延长.

4 结论

本文提出了一种基于模糊强化学习和果蝇优化的WSN数据聚合算法, 首先将网络区域划分成不同层次的网格簇, 其次根据剩余能量选取网格簇的簇头, 接着评估所有可能的数据聚合节点, 然后采用模糊强化学习选取最佳数据聚合节点, 最后利用果蝇优化算法动态定位外部通信节点. 本文所述算法适用于大规模密集型无线传感器网络, 可应用在工业生产信息采集等场景中.