2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
晶体结构搜索主要是产生新结构, 基于能量最低原理筛选优质结构的过程. 当前确定晶体结构能量有两种主要计算方法, 分子动力学[1]和密度泛函理论方法[2]. 前者代表软件如Lammps等, 后者代表软件如VASP[3,4]和CASTEP[5]等. 目前, 国内外已经报道了一些通过不同结构搜索算法, 结合预测结构能量的分子动力学或密度泛函理论等方法的晶体结构预测软件. 如基于随机搜索算法结合密度泛函理论的AIRSS[6]软件, 基于粒子群搜索算法结合密度泛函理论的CALYPSO[7], 基于杂化算法结合密度泛函理论的XtalOpt[8]软件, 基于遗传搜索算法结合分子动力学或密度泛函理论的USPEX[9]软件, 以及基于遗传算法同时结合了密度泛函理论和分子动力学的自适应遗传算法(Adaptive Genetic Algorithm, AGA)晶体结构预测软件[10]. 这些软件都是基于第一性原理或者分子动力学方法获取结构基态能量, 基于分子动力学方法, 计算速度快, 但是精度低. 而基于密度泛函理论方法计算精度高, 但是计算时间长, 尤其是随着晶体结构复杂度的上升, 其计算时间呈指数增长. 寻找一种既可以保证计算精度, 又可以降低计算成本的材料研究方法成为迫切需要解决的问题.
1 相关工作随着高性能计算和深度学习的发展, 机器学习在材料科学中越来越多的被使用, 可以准确预测材料的性能, 不断缩小材料科学与计算科学之间的差距. 哥伦比亚大学的Nongnuch Artrith研究组利用神经网络训练原子势函数, 用于快速预测结构能量, 并开发了原子能网络软件包(Atomic Energy Network, AENet)[11]. 普林斯顿大学Weinan课题组利用深度神经网络训练用于分子动力学计算的多体势函数[12-14], 所训练的相互作用势可以直接用于Lammps软件使用, 目前该方法已经封装为软件包DeePMD-kit. 中国科学院计算机网络信息中心刘学源等提出了用于结构预测的机器学习框架[15,16]. 德克萨斯大学奥斯汀分校的You等提出了多种机器学习算法来预测透明导体的生成焓和能带间隙, 采用的机器学习算法如最小二乘法、逐步回归法, 还有基于树的模型(随机森林模型和梯度提升模型)[17]. 日本东京大学的Ryo Yoshida课题组为了促进迁移学习的应用, 开发了一个XenonPy.MDL的预训练模型库, 这些预训练模型捕获了材料的公共特性. 克服了材料数据集数量有限的问题, 可以通过预先训练好的模型, 利用有限的训练数据来预测相关材料目标属性[18]. 西澳大利亚大学的James P. Doherty等课题组使用一种快速监督机器学习算法代替第一性原理计算预测材料弹性模量, 快速筛选新能量, 这种算法结合了线性回归、神经网络以及随机森林回归[19]. 南京邮电大学的李斌课题组等构建了深度神经网络模型, 通过学习开放量子材料数据(OQMD)中的生成焓参数训练模型, 并运用模型预测未知材料的生成焓进行预测, 达到量子力学软件的精度[20]. Lu等通过训练神经网络模型, 从仪器压痕中提取金属和合金的弹性特征, 作者建立了单缩进、双缩进和多重缩进求解逆问题的算法, 并提出几种multifidelity方法求解逆压痕问题[21].
综合考虑计算的准确性和时效性, 借助深度学习框架, 基于密度泛函理论计算数据集, 在结构预测过程中利用深度神经网络构建材料结构与能量之间的构效关系模型, 加快结构能量的预测, 并将该方法嵌入结构预测软件使用.
2 预测晶体结构能量的学习模型 2.1 神经网络和训练神经网络通常包含一个输入层, 一个输出层以及若干隐藏层, 输入层只接收输入信息, 通常为数据样本的特征向量, 经过隐藏分层和输出层的处理, 由输出层输出结果. 隐藏层的层数和节点数可以根据实际情况进行调整. 神经网络能够通过学习得到输入与输出的映射关系, 整个训练过程就是不断更新权重以及偏置值, 使得模型预测越来越准确. 通常每个层之间可以加入激活函数引入非线性因素. 图1为典型的单隐藏层神经网络.

|
图 1 单隐层神经网络 |
前向传播过程:
| $ a=\sigma ({W}_{1a}*{x}_{1}+{W}_{2a}*{x}_{2}+{\theta }_{1})$ | (1) |
| $ b=\sigma ({W}_{1b}*{x}_{1}+{W}_{2b}*{x}_{2}+{\theta }_{1})$ | (2) |
| $y = {W_{ay}}*a + {W_{by}}*b + {\theta _2}$ | (3) |
其中, σ为激活函数, 可以看出每个神经元的值由上一层的神经元的值与连接权重、偏置值以及激活函数共同决定.
反向传播算法(Back-Propagation, BP)[22,23]是神经网络中更新参数最经典的方法, 其代码逻辑如算法1.
算法1. 反向传播算法伪代码
输入: 训练集D, 学习率;
输出: 权重系数与偏置确定的多层前馈神经网络;
初始化神经网络中神经元的连接权重与偏置;
DO:
FOR all(xi,yi) in D DO
根据前向传播计算样本输出结果
根据计算结果计算各层梯度
根据输出结果及梯度更新权重系数及偏置
END FOR
UNTIL 停止条件
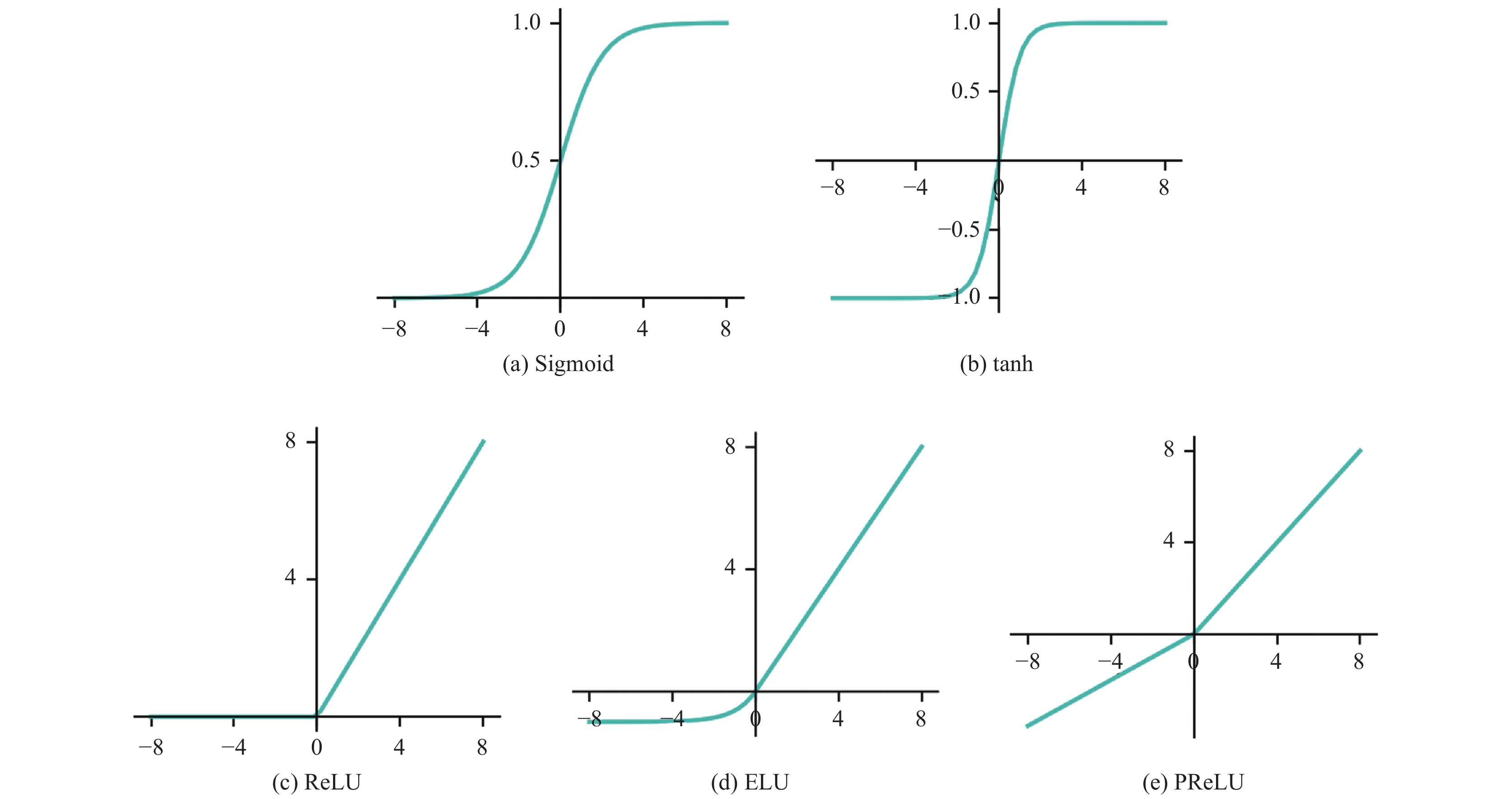
2.2 神经网络模型的主要技术 2.2.1 激活函数在人工神经网络中, 激活函数用于表示上层神经元输出与下层输入的非线性映射函数, 其主要作用就是增强神经网络的非线性建模能力. 如无特殊说明激活函数一般是非线性函数. 如果不用激活函数, 每一层的输出都是上一层输入的线性函数, 无论神经网络有多少层, 最终的输出都是初始输入的线性变换, 无法拟合现实中很多非线性问题. 引入激活函数后, 使得神经网络可以逼近任何非线性函数, 理论上可以拟合任意分布的数据. 常用的激活函数有Sigmoid函数[24]、tanh函数、Rectified Linear Unit (ReLU)函数[25,26]、ELU函数[27]、和Parametric Rectified Linear Unit(PReLU)函数[28]. 图2展示了这几种激活函数的图像.
|
图 2 常用激活函数图像 |
2.2.2 优化算法
权值更新算法是深度学习模型训练中相当重要的一个模块, 其决定参数更新的方向与速度, 好的权值更新算法和适当的优化参数能使模型更快更准地收敛. PyTorch包含一系列权值更新算法, 其接口通用性好, 也方便集成更加复杂的算法. PyTorch内集成SGD[29]、Adadelta[30]、Adagrad[31]、Root Mean Square Prop(RMSprop)[32], Adaptive Moment Estimation (Adam)[33]、Averaged Stochastic Gradient Descent (ASGD)[34]、Rprop[35]、LBFGS[36]等十余种权值更新算法.
学习率和BATCH_Size是深度学习中重要的超参数. 若学习率设置过小, 则收敛非常慢, 若设置过大, 则梯度会在最小值附近来回震荡. BATCH_Size的选择决定了梯度下降的方向, BATCH_Size选择过小, 随机性会加大, 多数情况难以收敛. 所以在实践中, 人们会选择较大的BATCH_Size, 较大的BATCH_Size可以减小训练时间, 提高内存利用率, 梯度下降方向较为准确, 不容易引起震荡; 但是, 盲目增大BATCH_Size也会导致如内存不够、模型的泛化能力下降[37]、收敛到sharp minimum[38]、迭代的次数增大等一系列问题.
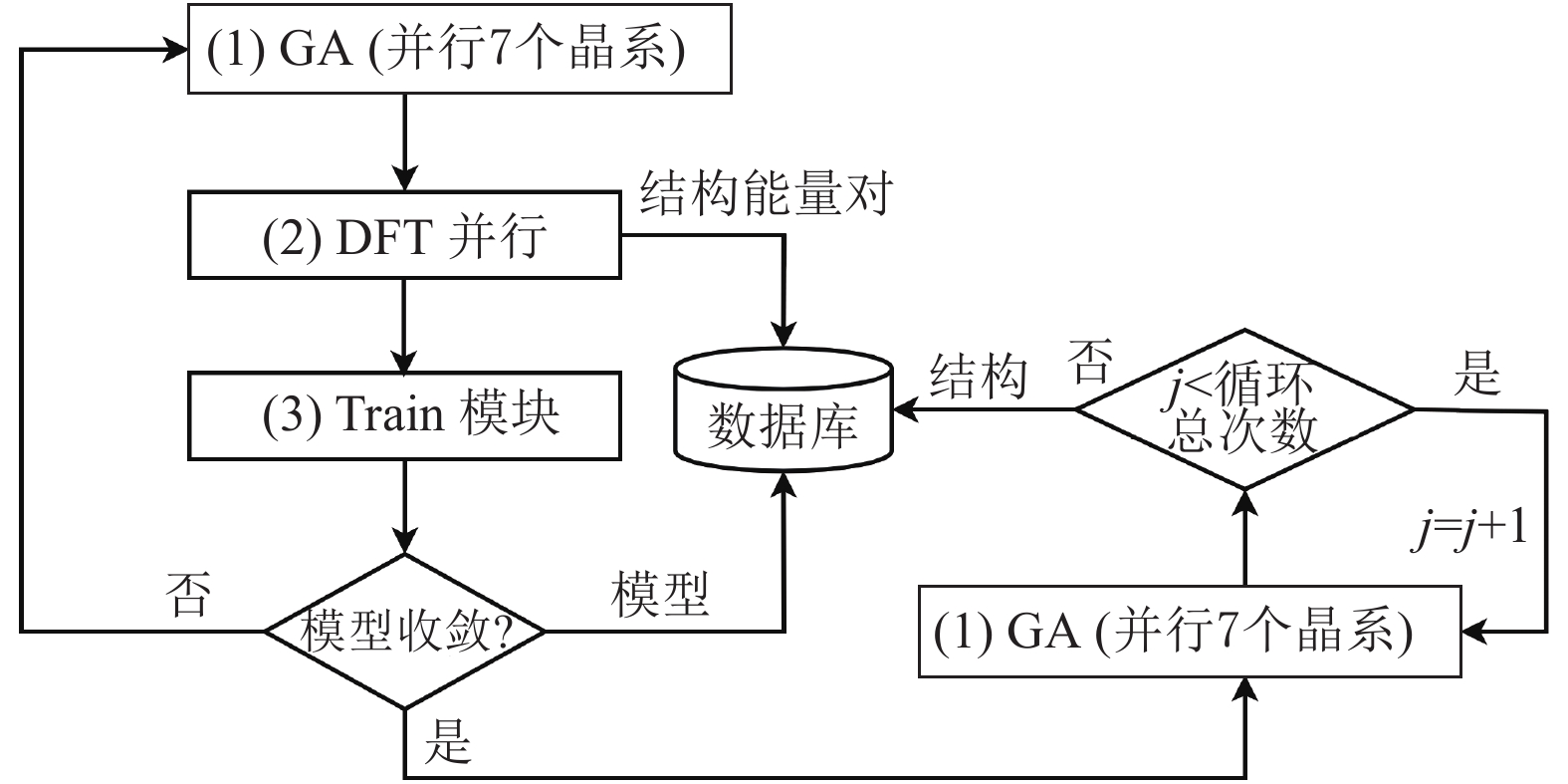
3 用于晶体结构预测的深度学习模型框架 3.1 模型训练总体框架设计 3.1.1 主流程晶体结构预测主流程如图3所示, 分为3个主要模块, 遗传算法(Genetic Algorithm, GA)、密度泛函理论(Density Functional Theory, DFT)计算和模型训练(Train), 3部分并行运行.
|
图 3 主流程图 |
(1) GA: 用于结构搜索. 并行运行7个晶系(立方晶系、四方晶系、方晶系、六方晶系、正交晶系、单斜晶系、三斜晶系), 利用神经网络势(或经验模型)预测能量, 推荐低能结构(每个晶系默认推荐16个, 每次循环共112个结构)开展DFT计算;
(2) DFT计算: 并行计算GA部分推荐结构的能量等信息. 剔除冗余结构, 将计算的结构和能量等计算结果存入数据库, 并加入Train模块的训练集;
(3) Train模块: 更新训练集后, 训练新模型, 更新GA部分里的神经网络势模型.
模型收敛性通过训练集的大小和模型误差两个标准决定. 首先, 确定训练集大小. 若训练集太小, 神经网络易过拟合, 训练集过多时间花费大, 而且易造成欠拟合, 经过多次实验及效果, 采用112×20作为训练集的最小量, 用户可以根据实际情况进行调整; 其次是模型误差, 通过实验发现, 当模型验证误差降到0.08左右即可很好的收敛, 用户也可以根据实际情况进行调整. 当模型收敛后, 不再进行DFT计算及模型更新, 只进行GA搜索, 收敛的模型存入到数据库中. 当GA搜索迭代完成时(默认循环总次数为20), 推荐最终的候选结构加入数据库.
3.1.2 GA模块详细流程软件的初始设置参数: GA的搜索迭代次数、结构内原子类型、各原子结构数量、原子体积等. 此外, 还需要准备描述各原子环境的指纹特征文件.
本文采用的遗传算法, 能量作为适应度值, 即能量越低, 结构越稳定. 在每一轮迭代中, 按照晶体结构的7个晶系并行搜索, 既保证了搜索的全面性也提高了搜索效率. 具体过程是先根据能量大小进行排序, 选择种群中前三分之一的低能结构[39](种群大小默认为64), 对坐标信息进行交叉变异操作, 产生下一代结构(默认产生下一代结构数量为16). 在迭代过程中, 为了防止陷入局部最优解, 一方面设置一定的变异概率(默认为0.05)基因突变, 突破搜索瓶颈; 另一方面, 我们采用多组不同的随机种子, 即产生多组不同的初始种群, 增加搜索多样性.
需要注意的是, 在没有初始模型的情况下, 通过经验模型迅速构建初始样本空间. 一旦训练出神经网络模型, 便采用神经网络势预测; 参数i为GA迭代过程中当前迭代轮数; 在没有训练出收敛的模型时, GA内搜索总次数可以设置为较小值(默认为30), 可以较快的训练出收敛模型. 模型收敛后增加GA内搜索总次数(默认为1500). 最后, 每个晶系推荐出16个低能结构共112个结构. 具体流程如图4所示.

|
图 4 GA模块流程图(以立方晶系为例, 其余晶系过程相同) |
3.2 模型训练流程实现及优化
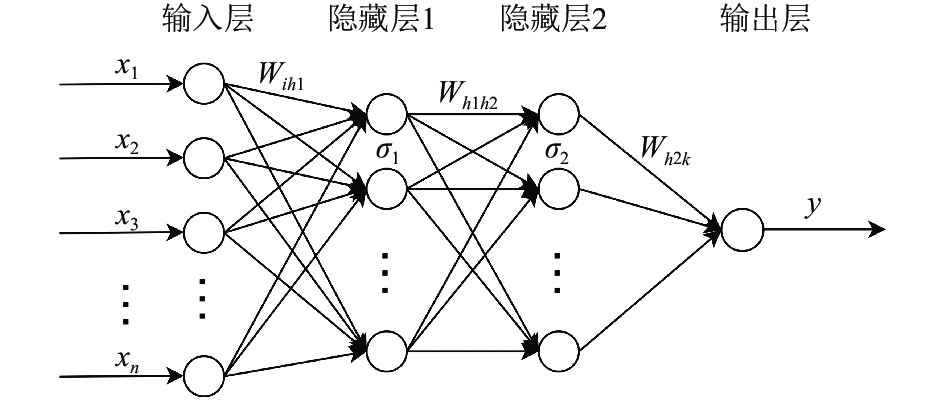
如图5所示, 我们使用4个神经网络层, 输入层神经元数量根据提取的原子特征数量灵活选取, 2个隐藏层各为10个神经元. 输入为能够满足原子平移性、对称性、置换性的原子局域环境描述子, 这些描述子可以转化为神经网络的输入特征向量, 目前, 提供了切比雪夫多项式[40]及Behler和Parrinello提出的对称函数[41,42]两种描述原子局域环境的描述方法. 输出为拟合的原子能量值. 隐藏层和输出层的神经元都有偏置参数, 由于更新过程与权重类似, 这里不再展开.
|
图 5 神经网络架构 |
(1)前向传播过程
隐藏层1输入:
| $ I_{h_1}=\sum_{i} W_{i h_1} x_{i} $ | (4) |
式中,
隐藏层1输出:
| $ {O_{h_1}} = {\sigma _1}({I_{h_1}}) = {\sigma _1}\left( {{\sum _i}{W_{ih_1}}{x_i}} \right)$ | (5) |
式中, σ1为激活函数.
隐藏层2输入:
| $ I_{h_2}=\sum_{h_1} W_{h_1 h_2} O_{h_1} $ | (6) |
式中,
隐藏层2输出:
| $ O_{h_2}=\sigma_{2}\left(I_{h_2}\right)=\sigma_{2}\left(\sum_{i} W_{h_1 h_2} O_{h_1}\right) $ | (7) |
式中, σ2为激活函数.
输出层:
| $y = O = \mathop \sum \limits_i {W_{h_2k}}{O_{h_2}}$ | (8) |
式中,
(2)反向传播: 以第
隐藏层2到输出层的权重更新:
| $ W_{h_2 k}^{l+1}=W_{h_2 k}^{l}-\eta \cdot \frac{\partial E_{r r}}{\partial W_{h_2 k}^{l}}=W_{h_2 k}^{l}-\eta \cdot \frac{\partial E_{r r}}{\partial y} \cdot \frac{\partial y}{\partial W_{h_2 k}^{l}} $ | (9) |
隐藏层1到隐藏层2的权重更新:
| $\begin{split} W_{h1h2}^{l + 1} &= W_{h1h2}^l-\eta \cdot\frac{{\partial {E_{rr}}}}{{\partial W_{h1h2}^l}}\\ & =W_{h1h2}^l-\eta \cdot\frac{{\partial {E_{rr}}}}{{\partial y}}\cdot\frac{{\partial y}}{{\partial {O_{h2}}}}\cdot\frac{{\partial {O_{h2}}}}{{\partial {I_{h2}}}}\cdot\frac{{\partial {I_{h2}}}}{{\partial W_{h1h2}^l}}\end{split} $ | (10) |
输入层到隐藏层1的权重更新:
| $\begin{split} W_{ih_1}^{l + 1} &= W_{ih_1}^l-\eta \cdot\frac{{\partial {E_{rr}}}}{{\partial W_{ih_1}^l}} \\ & = W_{i h_1}^{l}-\eta \cdot \frac{\partial E_{r r}}{\partial y} \cdot \frac{\partial y}{\partial O_{h_2}} \cdot \frac{\partial O_{h_2}}{\partial I_{h_2}} \cdot \frac{\partial I_{h_2}}{\partial O_{h_1}} \cdot \frac{\partial O_{h_1}}{\partial I_{h_1}} \cdot \frac{\partial I_{h_1}}{\partial W_{i h_1}^{l}}\end{split} $ | (11) |
这样整个神经网络完成一次参数更新.
需要注意的是, 由于我们将总能量拆分为单个原子的能量, 最后进行累加, 所以与传统的神经网络训练过程不同, 每个原子的能量并不是已知的, 因此权重参数不能直接拟合到样本中. 我们对每个结构中的原子能量累加后再进行误差计算和反向传播.
3.3 关键技术的选取 3.3.1 测试数据集测试数据集中包含了原子数为6、9、12、18和24的TiO2晶胞, 随机生成Ti原子与O原子的配比共计15种, 包含6056个晶体结构. 每种组分包含的晶体结构数目见表1.
| 表 1 测试数据集TiO2结构信息 |
3.3.2 激活函数的选取
为测试激活函数对材料结构预测软件中训练模型的影响, 采用目前深度学习常用的Adam优化算法, 设置学习率为0.0001, 设置BATCH_Size为32测试不同激活函数对模型训练的影响.
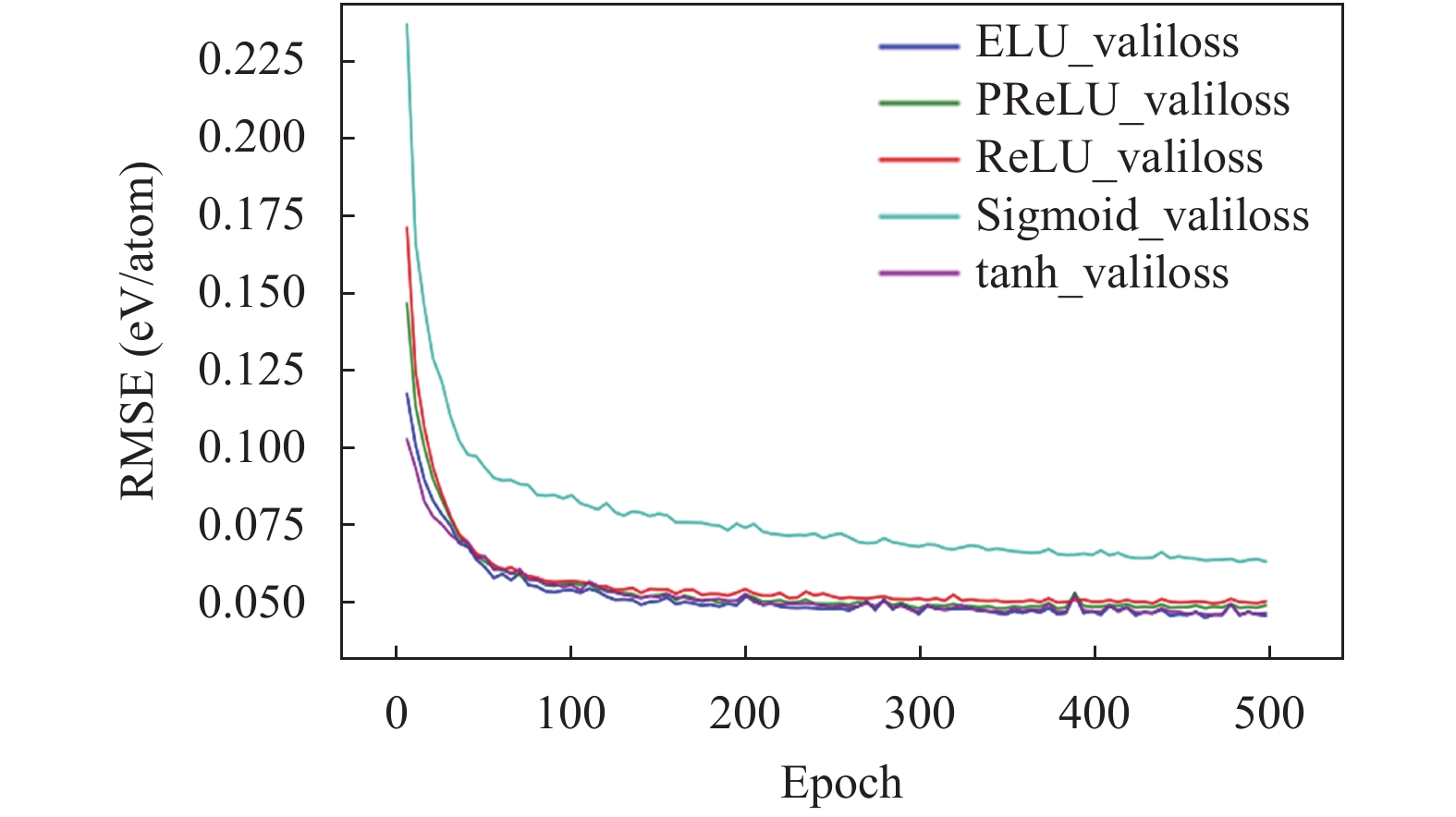
从图6可以看出, 相比于Sigmoid函数, 其他激活函数收敛效果明显较好, tanh在开始阶段收敛较快, 最终的收敛效果几个激活函数大致相似, 综合考虑, 我们后续实验均采用tanh激活函数.
|
图 6 不同激活函数的损失变化趋势图 |
3.3.3 优化算法选取
学习率和BATCH大小的选取也会影响优化算法的效果, 我们综合分析了学习率和BATCH大小对8种优化算法的影响, 采取5种BATCH_Size, 0.00001–0.1之间选取5种学习率进行测试. 测试过程中随机选取了5组随机种子, 图7中结果为5组数据的平均值.
图7中Adadelta、Adam、Adamax、ASGD、LBFGS、RMSprop、Rprop、SGD算法分别用灰色、黑色、蓝色、青绿色、洋红色、黄色、红色、绿色表示; BATCH_Size的值1、8、16、32和Full分别由圆点、实心方形、实心五角、倒三角、十字表示.
可以看出在BATCH_Size为1和8时, 多数优化算法表现较好, 同时也可以看出盲目增大BATCH_Size, 模型的泛化能力会降低, 并且可能陷入sharp minimum. Adadelta适合较大的学习率, 而RMSprop、Rprop、Adam、Adamax适合选取较小的学习率.
学习率和BATCH_Size搭配最优情况下, Adadelta、Adam、Adamax、RMSprop的损失值均能达到0.043左右, 均能收敛到理想的模型.

|
图 7 优化算法、BATCH_Size、学习率大小对模型性能的影响 |
3.4 训练集优化
为剔除训练集中的冗余结构, 在模型训练过程中, 并不是将每次循环DFT计算的所有结构都加入到训练集中, 通过两步剔除冗余结构. 首先, 考虑到每次循环的GA都是从头搜索, 所以不同循环轮次之间可能会产生相同的结构, 对模型训练改进意义不大. 故剔除每个循环伦次的重复冗余结构, 不再加入训练集. 然后, 为提高模型训练效率, 设定一个最小误差项, ΔE=min_loss*n_atom, 其中n_atom为原子数. 若模型预测的结构总能量与DFT计算的总能量的差值低于此值, 则认为此结构对模型训练改进意义不大, 该结构不再加入训练集.
此外, 为防止模型出现过拟合的情况, 在模型更新中我们采用了机器学习中比较典型的早停法[23].
4 软件性能分析 4.1 主要参数设置及搜索策略为了测试所提出的模型的性能以及实验参数的设置, 我们以Si单晶、TiO2和CaTiO3三种常见的晶体结构的搜索为例, 对本文所提出的模型进行测试, 并与实验结果进行对比分析.
首先, 确定实验参数. Si单晶和TiO2化合物的原子局域环境的展开式采用Behler和Parrinello提出的不变对称函数表示, 搜索激活函数选用双曲正切函数(tanh), 优化算法为Adam, 学习率设置为0.0001, BATCH_Size设置为1. CaTiO3的原子局域环境的展开式采用基于切比雪夫多项式表示, 激活函数选用双曲正切函数(tanh), 优化算法为Adamax, 学习率设置为0.001, BATCH_Size设置为8. 然后, 开展模型训练和结构搜索. 初始结构根据七大晶系分别搜索, 七大晶系的搜索采用并行计算, 每种晶系每个循环轮次推荐16个低能晶体结构用于开展DFT计算, 然后加入训练集去训练更优的模型, 直至模型收敛. 将收敛的模型用于结构搜索. 每个晶系默认按20个随机种子搜索结构, 每个种子推荐出16个候选结构, 最后每个晶系按模型预测能量排序推荐出10个低能结构, 然后进行DFT计算, 根据计算能量大小推荐晶体结构.
4.2 实验结果分析采用遗传算法搜索晶体结构, 基于深度学习训练模型预测晶体结构的能量值. 通过该方法预测的结构晶格常数信息和对应的能量值与DFT计算结果见表2, E为DFT计算总能量. 表2可以看出, 3种结构的晶格常数的最大误差分别为: 0 、6.88%和0. 在满足均方根误差小于0.08 eV/atom的模型下, 预测的3种稳定结构总能量与实验测定稳定结构的总能量差值分别为: 0.34 eV、1.41 eV以及0.21 eV. 预测晶体结构与实验结构示意图见图8, 结构中原子坐标见附录.
| 表 2 3种晶体结构预测结果与实验结果对比(单位: eV) |
从图8可以看出, 基于深度学习框架实现的晶体结构预测软件, 对于单胞中原子数目较少的Si单晶和CaTiO3结构的能量预测都具有很好的效果, 随着元素种类的增加, 模型误差增大, 因此对于单胞中原子数较多的原子还需要增大训练集的多样性. 另外, 通过图8也可以看出, 用于结构搜索的遗传算法, 随着元素种类的增加, 结构的搜索效果逐渐降低, CaTiO3结构的成键图8(f)以及TiO2结构的原子点位图8(d)与实验结构有所偏移. 因此, 在结构搜索中需要增加种子数和迭代次数来修正.

|
图 8 预测晶体结构与实验观测结构 |
相比于基于密度泛函理论的第一性原理方法, 神经网络模型预测晶体结构能量节省了更多的计算资源和时间. 为保证结构搜索的完整性, 需要搜索的晶体结构数量巨大, 如果所有结构都采用第一性原理方法计算结构能量几乎是无法完成的, 我们提出的面向材料结构预测的深度学习方法, 只需对要少量有针对性的结构开展第一性原理计算, 作为神经网络训练的数据, 即可训练出精度较高的能量预测模型, 从而实现其他结构能量的快速预测. 此外, 随着晶体结构复杂度的增加, 第一性原理计算的时间成本呈指数增加, 而我们提出的深度学习方法受结构复杂度影响较小, 同样只需要少量的第一性原理计算, 构建高精度的神经网络模型预测晶体结构能量. 通过该方法在保证计算精度的前提下, 既提高了计算效率, 又克服了部分复杂体系无法开展大量计算的困难.
5 结论本研究针对批量材料结构能量预测效率问题实现了一种用于材料结构预测的基深度学习方法, 通过深入的分析和研究, 对深度学习模型所需的训练策略、测试集数据筛选方法、优化算法及其对应的学习率等参数进行了优化. 并将深度学习框架应用到材料结构的预测中, 预测的晶体结构参数与实验发现晶体结构参数相吻合. 该方法可以有效地提高材料结构预测效率, 加快新材料的研发.
| [1] |
Andersen HC. Molecular dynamics simulations at constant pressure and/or temperature. The Journal of Chemical Physics, 1980, 72(4): 2384-2393. DOI:10.1063/1.439486 |
| [2] |
Becke AD. Density-functional thermochemistry. III. The role of exact exchange. The Journal of Chemical Physics, 1993, 98(7): 5648-5652. DOI:10.1063/1.464913 |
| [3] |
Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science, 1996, 6(1): 15-50. DOI:10.1016/0927-0256(96)00008-0 |
| [4] |
Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set
. Physical Review B, 1996, 54(16): 11169-11186. DOI:10.1103/PhysRevB.54.11169 |
| [5] |
Clark SJ, Segall MD, Pickard CJ, et al. First principles methods using CASTEP. Zeitschrift für Kristallographie-Crystalline Materials, 2005, 220(5–6): 567-570. DOI:10.1524/zkri.220.5.567.65075 |
| [6] |
Liborio L, Sturniolo S, Jochym D. Computational prediction of muon stopping sites using ab initio random structure searching (AIRSS)
. The Journal of Chemical Physics, 2018, 148(13): 134114. DOI:10.1063/1.5024450 |
| [7] |
Wang YC, Lv J, Zhu L, et al. CALYPSO: A method for crystal structure prediction. Computer Physics Communications, 2012, 183(10): 2063-2070. DOI:10.1016/j.cpc.2012.05.008 |
| [8] |
Lonie DC, Zurek E. XtalOpt: An open-source evolutionary algorithm for crystal structure prediction. Computer Physics Communications, 2011, 182(2): 372-387. DOI:10.1016/j.cpc.2010.07.048 |
| [9] |
Glass CW, Oganov AR, Hansen N. USPEX—Evolutionary crystal structure prediction. Computer Physics Communications, 2006, 175(11–12): 713-720. DOI:10.1016/j.cpc.2006.07.020 |
| [10] |
Wu SQ, Ji M, Wang CZ, et al. An adaptive genetic algorithm for crystal structure prediction. Journal of Physics: Condensed Matter, 2014, 26(3): 035402. DOI:10.1088/0953-8984/26/3/035402 |
| [11] |
Artrith N, Urban A. An implementation of artificial neural-network potentials for atomistic materials simulations: Performance for TiO2. Computational Materials Science, 2016, 114: 135-150. DOI:10.1016/j.commatsci.2015.11.047 |
| [12] |
Wang H, Zhang LF, Han JQ, et al. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Computer Physics Communications, 2018, 228: 178-184. DOI:10.1016/j.cpc.2018.03.016 |
| [13] |
Zhang LF, Han JQ, Wang H, et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, QC, Cananda. 2018. 4441–4451.
|
| [14] |
Zhang LF, Lin DY, Wang H, et al. Active learning of uniformly accurate interatomic potentials for materials simulation. Physical Review Materials, 2019, 3(2): 023804. DOI:10.1103/PhysRevMaterials.3.023804 |
| [15] |
刘学源, 王彦棡, 任荟颖, 等. 基于PyTorch的晶体结构势预测. 科研信息化技术与应用, 2019, 10(2): 61–70.
|
| [16] |
刘学源. 基于机器学习的晶体结构预测软件研制[硕士学位论文]. 北京. 中国科学院计算机网络信息中心. 2019.
|
| [17] |
You ZY. Machine learning and statistical analysis in material property prediction [Master’s thesis]. Austin: University of Texas at Austin, 2018.
|
| [18] |
Yamada H, Liu C, Wu S, et al. Predicting materials properties with little data using shotgun transfer learning. ACS Central Science, 2019, 5(10): 1717-1730. DOI:10.1021/acscentsci.9b00804 |
| [19] |
Cendra C. A data-driven approach for predicting elastic properties of inorganic materials [Technical report]. Stanford University, Department of Materials Science and Engineering, 2018. 1–6.
|
| [20] |
提磊, 吴思璇, 李斌, 等. 机器学习在材料性质预测中的运用. 凝聚态物理学进展, 2020, 9(2): 11-19. DOI:10.12677/cmp.2020.92002 |
| [21] |
Lu L, Dao M, Kumar P, et al. Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proceedings of the National Academy of Sciences of the United States of America, 2020, 117(13): 7052-7062. DOI:10.1073/pnas.1922210117 |
| [22] |
Sazli M H. A brief review of feed-forward neural networks. Communications Faculty of Science University of Ankara, 2006, 50(1): 11-17. DOI:10.1501/commua1-2_0000000026 |
| [23] |
周志华. 机器学习. 北京: 清华大学出版社, 2016.
|
| [24] |
黄毅, 段修生, 孙世宇, 等. 基于改进Sigmoid激活函数的深度神经网络训练算法研究. 计算机测量与控制, 2017, 25(2): 126-129. DOI:10.16526/j.cnki.11-4762/tp.2017.02.035 |
| [25] |
Nair V, Hinton G E. Rectified linear units improve restricted Boltzmann machines. Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel. 2010.807–814.
|
| [26] |
Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, FL, USA. 2011. 315–323.
|
| [27] |
Clevert DA, Unterthiner T, Hochreiter S. Fast and accurate deep network learning by Exponential Linear Units (ELUs). Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico. 2016.
|
| [28] |
He KM, Zhang XY, Ren SQ, et al. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile. 2015. 1026–1034.
|
| [29] |
Sutskever I, Martens J, Dahl G, et al. On the importance of initialization and momentum in deep learning. Proceedings of the 30th International Conference on Machine Learning. Atlanta, GA, USA. 2013. 1139–1147.
|
| [30] |
Zeiler MD. Adadelta: An adaptive learning rate method. arXiv: 1212.5701, 2012.
|
| [31] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 2011, 12: 2121-2159. DOI:10.5555/1953048.2021068 |
| [32] |
Hinton G, Srivastava N, Swersky K. RMSPROP: Divide the gradient by a running average of its recent magnitude. Neural Networks for Machine Learning, 2012, 4: 26–31.
|
| [33] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference for Learning Representations. San Diego, CA, USA. 2015. 1–15.
|
| [34] |
Schmidt M, Le Roux N, Bach F. Minimizing finite sums with the stochastic average gradient. Mathematical Programming, 2017, 162(1–2): 83-112. DOI:10.1007/s10107-016-1030-6 |
| [35] |
Riedmiller M, Braun H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. Proceedings of IEEE International Conference on Neural Networks. San Francisco, CA, USA. 1993. 586–591.
|
| [36] |
Byrd RH, Lu PH, Nocedal J, et al. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing, 1995, 16(5): 1190-1208. DOI:10.1137/0916069 |
| [37] |
Goyal P, Dollár P, Girshick R, et al. Accurate, large minibatch SGD: Training ImageNet in 1 hour. arXiv: 1706.02677, 2017.
|
| [38] |
Keskar NS, Mudigere D, Nocedal J, et al. On large-batch training for deep learning: Generalization gap and sharp minima. Proceedings of the 5th International Conference on Learning Representations. Toulon, France. 2017.
|
| [39] |
李敏, 黄敏, 程智锋, 等. 遗传算法在路径规划上的应用. 计算机系统应用, 2020, 29(8): 255-260. DOI:10.15888/j.cnki.csa.007417 |
| [40] |
Artrith N, Urban A, Ceder G. Efficient and accurate machine-learning interpolation of atomic energies in compositions with many species. Physical Review B, 2017, 96(1): 014112. DOI:10.1103/PhysRevB.96.014112 |
| [41] |
Behler J, Martoňák R, Donadio D, et al. Metadynamics simulations of the high-pressure phases of silicon employing a high-dimensional neural network potential. Physical Review Letters, 2008, 100(18): 185501. DOI:10.1103/PhysRevLett.100.185501 |
| [42] |
Behler J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. Journal of Chemical Physics, 2011, 134(7): 074106. DOI:10.1063/1.3553717 |
 2021, Vol. 30
2021, Vol. 30



