长期以来, 社区检测一直是数据挖掘领域的一个研究热点. 该任务旨在基于仅由节点和边构成的图数据, 将相似的节点聚集到社区当中, 完成节点-社区隶属关系的分配, 期望社区内点的连接相比社区外更密集. 例如在论文引用关系网络中, 相似方向的论文会被分到同一小组^[1,2]; 在网页超链接网络中, 相似内容的网页将被聚集^[3]. 该任务在刻画图数据的社区分布形态的同时, 也影响了很多其他图学习任务的发展, 例如图表示学习和图链路预测任务等.

目前的社区检测算法主要分为两类: 非重叠式和重叠式的社区检测^[4,5]. 非重叠式社区检测的目标是识别不相交的社区, 但社区不相交的假设在很多数据集上是难以成立的. 例如在社交网络中, 一个人可能因为身份或兴趣的多样而同时归属于多个社区. 因此社区间存在相交关系, 这种重叠式的社区分布在假设上更合理^[6]. 重叠的假设意味着社区检测算法需要对每个节点学习更多的信息, 因而带来了更高的复杂性挑战. 近几年很多研究工作^[2,4,5,7]都着眼于重叠式的社区检测, 证实了重叠式的社区建模能带来更精准的结果.

随着图数据的多样化和复杂化, 不论是非重叠还是重叠的社区分布, 这类传统的平坦式社区分布形态已经不能很好的描述复杂图数据的社区分布, 复杂网络中的社区结构通常是分层的^[8]. 针对这个问题, 之前研究提出, 在社区检测的基础上, 用一棵树来表达社区之间的层级关系^[9,10]. 在优化的过程中, 需要把网络中的节点划分到树上的不同社区中. 例如Bhowmick和Meneni等^[9]提出基于Louvain^[11]算法递归的划分网络, 从而将较大的社区拆解为小的社区, 求解节点属于树上每一层的哪个社区^[9].

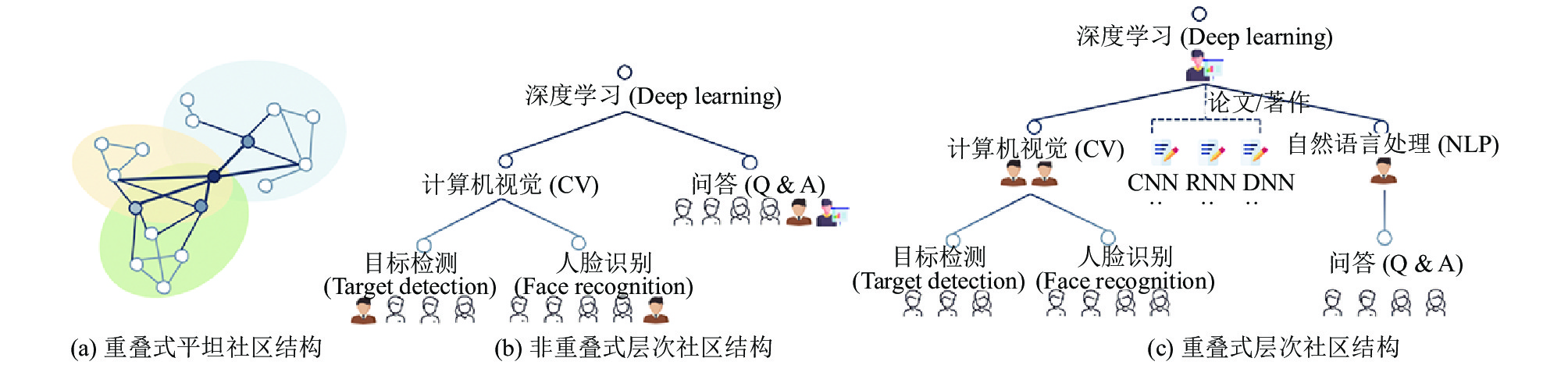
但是现有层次化社区检测方法都只能建模非重叠的社区分布, 这使得这些方法很难更加精准的描述网络结构. 举例来说, 在论文作者合著关系图数据中, 同时在多个领域有研究工作的作者, 在平坦社区结构中, 会同时归属于多个社区; 在层次社区结构中, 其归类应比单一领域内紧密合作的作者社区具有更高的层次等级. 如图1所示, 一些同时涉猎计算机视觉(CV)多个领域的作者与具体领域的作者相比应具有更高等级; 同时和计算机视觉, 自然语言处理(NLP)多个任务领域合作的作者, 应比单任务领域的作者们具有更高等级, 因此用重叠式层次结构描述该数据的社区形态是必要的. 重叠式层次化社区检测任务的主要难点在于, 由于层次结构建模问题本身被证明是一个NP问题^[12], 所以之前方法通常都用启发式算法来求解, 在此基础上就很难再加入重叠信息的建模.

在这篇文章中, 我们提出利用图表示学习来解决这个问题. 具体而言, 我们利用了节点嵌入表示学习 ^[13,14], 把每个节点映射到一个实数向量上, 利用这些向量来描述图的拓扑结构, 然后与层次化重叠社区检测做联合建模, 从而同时求得两个任务上的解.

为了实现上述框架, 在本文中, 对于如何联合优化节点嵌入和重叠式层次社区检测任务, 我们提出了轻量的解决方案: 首先, 我们将社区的层次结构定义为一颗树的形态, 称之为社区树, 该树上层的社区具有更高的层次等级. 其次, 给定一颗社区树, 自定义基于节点嵌入和层次结构的距离算法, 通过最小化有链接的成对节点间的距离, 完成节点嵌入和社区嵌入表示的更新, 以及节点-社区隶属关系的分配. 我们的方法可以灵活的适应任意的层次结构, 不受深度和宽度的限制. 与之前非重叠层次化社区检测算法相比, 我们的优势在于:

(1) 我们是第一个可以对节点嵌入和层次化社区检测任务做联合建模的方法. 之前工作表明, 节点嵌入与社区检测任务是高度相关的, 联合建模会带来互惠的优势: ① 节点嵌入将离散的数据映射到连续的高维空间中, 可以捕获局部信息, 为社区检测任务提供支持^[1,2,7]; ② 社区检测的节点-社区隶属关系可以为节点嵌入提供全局信息^[1,7]. 实验证明了我们框架的有效性.

(2) 我们是第一个在层次化社区检测中应用梯度下降的算法. 之前的层次化检测方法通常使用启发式学习来把每个节点映射到一个社区上. 但是, 启发式方法往往是分离的优化过程, 无法和其它有效的连续优化算法组合获得更好的结果. 另一方面, 基于梯度的连续优化方法不仅可以灵活的与任意相关任务组合优化, 还可以有效地在专用硬件(例如GPU)上运行.

后文组织如下: 第1节介绍层次社区检测任务定义; 第2节介绍自适应的重叠式层次社区检测方法; 第3节介绍实验设置以及实验结果; 第4节进行总结.

1 层次社区检测任务

对于包含 $N$ 个节点的无向同质图 $G = (V,E)$ , 其中 $V$ 表示节点, 满足 $\left| V \right|{\rm{ = }}N$ ; $E$ 表示边. 对于任意一对节点 ${v_i},{v_j} \in V$ 都存在一条边 ${e_{ij}} \in E$ 且 ${e_{ij}}{\rm{ = \{ }}0,1{\rm{\} }}$ , ${e_{ij}}{\rm{ = }}0$ 表示边不存在, 否则存在.

对于包含 $t$ 个社区的社区树 ${T_t}$ , 树上的每个叶节点和非叶节点都表示社区 $c = 1,2,\cdots,t$ . 非重叠式社区树和重叠式社区树的区别在于: 前者的每个非叶节点社区仅是底层社区的合并; 后者的非叶节点社区是包含若干节点的独立社区, 其内部节点无法被下分到任意低层社区中.

层次社区检测任务的目标是: 基于给定的任意形态的社区树 ${T_{_t}}$ 和图 $G$ 的链路关系信息 $E$ , 为每个图节点 ${v_i}$ 找到最合适的归属社区 ${c_i}$ , 使得每个社区内节点间边的密度远高于社区间边的密度.

之前启发式的工作^[9,10]采用贪心策略或遗传算法做出决策, 但实际上是分离的两步策略, 简单来说: (1)首先进行图节点嵌入表示学习, 通过映射函数 $F:{v_i} \to {{\phi} _{ i}} \in {\mathbb{R}^d}$ 将图节点 ${v_i}$ 从原始离散空间映射到 $d$ 维连续空间. 对于任意有真实连接关系的 ${e_{ij}}{\rm{ = 1}}$ 的节点 ${v_i}$ 和 ${v_j}$ , 其嵌入向量 ${{\phi} _{ i}}$ 和 ${{\phi} _{ j}}$ 在空间上的距离应该尽可能的近, 反之亦然. (2)随后, 利用节点嵌入表示启发式地探索层次社区结构. 这种分离的策略不能使得节点嵌入和社区检测两个任务互利互惠^[1,2,7], 此外, 非重叠社区分布假设的不合理性限制了这些工作仅能建模简单的浅层非重叠式社区树.

为了更合理的描述复杂图数据的社区分布, 我们提出建模重叠式层次社区结构, 部分图节点 ${v_i}$ 只隶属于社区树 ${T_{_t}}$ 中的非叶节点社区, 表示重叠部分. 为了消解层次结构和重叠结构带来的建模难题, 我们引入图表示学习任务来构建双任务优化模型, 任务目标是:

(1)学习节点-社区一一对应的隶属关系.

(2)学习节点和社区的 $d$ 维嵌入表示.

基于这样的定义, 不仅可以获得图数据的层次社区分布, 为不同粒度的分析任务提供支持; 也可以获得其节点的嵌入表示, 应用于丰富的下游任务.

2 基于梯度的重叠式层次社区检测算法

对于固定的重叠式社区树 ${T_t}$ , 我们需要在嵌入表示信息的指引下, 将图节点放置到社区树的不同社区中, 形成节点-社区的隶属关系; 同时需要根据分配的隶属关系, 更新节点和社区的嵌入表示.

2.1 节点-社区隶属关系的分配

我们定义图节点 ${v_i}$ 归属于社区 $c = 1,2,\cdots,t$ 的概率服从多项式分布: $P(C|{v_i}) = {\rho _{ic}}$ , 其中 $\;{\rho _{ic}} \in [0,1]$ 且 $\displaystyle\sum\nolimits_{c = 1}^t {{\rho _{ic}} = 1} $ .

为了使得节点和社区的嵌入表示能够指导节点-社区隶属关系的分配, 我们将节点和社区嵌入到相同的表示空间当中, 基于空间距离决策隶属关系. 因此, 进一步定义图节点 ${v_i} \in V$ 的 $d$ 维嵌入表示为 ${{\phi} _{ i}} \in {\mathbb{R}^d}$ , 社区 $c = {\rm{\{ }}1,2,\cdots,t{\rm{\} }}$ 的 $d$ 维嵌入表示为 ${{\varphi} _c} \in {\mathbb{R}^d}$ . 通过将节点和社区从原始不同的离散空间嵌入映射到相同的 $d$ 维连续空间, 可以定义节点 ${v_i}$ 归属于社区 $c$ 的概率为空间内两向量的乘积:

${\rho _{ic}} = softmax\left( {{{\phi} _{ i}}^{\rm{T}}{{\varphi} _c}} \right)$

2.2 节点和社区嵌入表示的学习

为了和原始数据尽可能保持一致, 我们期望在图数据中有真实连接 ${e_{ij}}{\rm{ = 1}}$ 的节点 ${v_i}$ 和 ${v_j}$ , 在社区树 ${T_t}$ 上的距离尽可能相近. 由于层次社区检测任务和节点嵌入表示任务分别描述了图数据的整体分配和局部信息, 因此在双任务联合优化时, 我们同时考虑成对节点隶属社区的距离和它们嵌入表示的距离, 提出了成对节点的距离计算方法.

当给定一对节点 ${v_i}$ 和 ${v_j}$ 时, 根据节点和社区的嵌入表示, 可以获得节点-社区隶属关系的概率 $\;{\rho _{ic}}$ 和 $\;{\rho _{jc}}$ , 分别选取概率最大的社区 ${c_i}$ 和 ${c_j}$ 作为社区树 ${T_t}$ 上的隶属社区. 社区间的距离 $\Lambda ({c_i},{c_j})$ 被定义为:

$\Lambda ({c_i},{c_j}) = distance({c_i},{c_o}) + distance({c_j},{c_o})$

其中, ${c_o}$ 为社区 ${c_i}$ 和 ${c_j}$ 在树上的最小公共祖先, $distance( \cdot , \cdot )$ 表示树上两节点的最短路径长度. 因此我们定义节点 ${v_i}$ 和 ${v_j}$ 在社区树上的距离:

${d_{ij}} = {\mathbb{E}_{{c_i} \sim P(C|{v_i}),{c_j} \sim P(C|{v_j})}}\left[ {\Lambda ({c_i},{c_j})} \right] = {{\bf{\rho }}_i}^{\rm{T}}\Lambda {{\bf{\rho }}_j}$

其中, $\Lambda \in {\mathbb{R}^{t \times t}}$ 是社区树上所有社区的距离矩阵, $\;{{\bf{\rho }}_i} \in {\mathbb{R}^t}$ 是节点 ${v_i}$ 隶属社区概率 $\;{\rho _{ic}}$ 的向量表示. 我们的目标是期望有真实连接的成对节点 ${v_i}$ 和 ${v_j}$ 在社区树上的距离 ${d_{ij}}$ 尽可能小, 反之亦然, 因此损失函数为:

$\ell (\varphi , \phi ) = - {\Sigma _{{v_i}}}{\Sigma _{{v_j},{v_k}}}\max(0,\beta + {d_{ik}} - {d_{ij}})$

其中, ${e_{ij}}{\rm{ = }}1,{e_{ik}}{\rm{ = 0}}$ ; $\;\beta $ 是一个大于0的常数, 用于控制正负样本的差距. 基于这样的正负样本距离损失函数, 可以在学习过程中不断更新节点和社区的嵌入表示 $\{ {{\phi} _{ i}}\} _{i = 1}^N, $ $ \{ {{\varphi} _c}\} _{c = 1}^t$ , 从而更新节点基于社区树的概率分布, 最终获得节点-社区的最优隶属关系 $\{ {\rho _{ic}}\} _{c = 1}^t$ .

2.3 完整的基于梯度的优化框架

基于给定的一颗重叠式社区树, 可以通过节点和社区的嵌入表示计算节点-社区隶属关系, 进而计算成对节点间的距离. 通过最小化距离损失来调整节点和社区的嵌入表示, 更新隶属关系. 如图2所示, 反复这一学习过程直至收敛, 就可得到最终解.

整体的算法描述如算法1.

算法1. 基于梯度的重叠式层次社区检测算法

1) 初始化: 给定真实图数据 $\scriptstyle G = (V,E)$ , 定义重叠式社区树 $\scriptstyle{T_{_t}}$ 和距离矩阵 $\scriptstyle{\Lambda _t}$ . 随机生成图节点和社区的 $\scriptstyle d$ 维嵌入表示 $\scriptstyle \varphi ,\; \phi $ .

2) 基于节点和社区的嵌入表示 $\scriptstyle \varphi ,\; \phi $ 计算节点-社区隶属概率, 确认隶属关系 $\scriptstyle\{ {\rho _{ic}}\} _{c = 1}^{t{\rm{ + }}1}$ .

3) 基于隶属关系 $\scriptstyle \{ {\rho _{ic}}\} _{c = 1}^{t{\rm{ + }}1}$ 计算节点间距离 $\scriptstyle{d_{ij}}$ .

4) 基于损失函数 $\scriptstyle \ell (\varphi ,\phi )$ , 和距离矩阵 $\scriptstyle {\Lambda _t}$ 更新节点和社区的嵌入表示 $\scriptstyle \varphi,\phi$ 以及隶属关系 $\scriptstyle \{ {\rho _{ic}}\} _{c = 1}^{t{\rm{ + }}1}$ .

5) 循环过程2)–4)直至收敛.

上述算法展示了如何基于自定义的距离计算方式, 自适应任意的重叠式层次结构, 进行节点嵌入表示学习和节点-社区隶属关系分配. 两个基于图数据的基础任务共享知识, 互相指引, 实现了端到端的联合优化模型, 两个任务的表现共同得到了提升.

值得注意的是, 我们将所有的距离计算融合为矩阵计算, 极大的提升了算法效率.

3 实验分析 3.1 实验设置

我们分别使用Aminer数据集^[15]和Wiki-vote数据集进行了实验. Aminer数据集是从dblp学术论文网站收集的4258 615组引文(cocitation)关系, 以及相应的论文信息和作者信息. 我们去除了没有任何引用关系的论文数据后, 共获得包含12 840个节点和190 658条边. Wiki-vote数据集是维基百科数据集, 包含3135个节点和95 028条边.

我们使用6种社区检测算法作为基线模型:

ComE ^[2]和MNMF^[7]: 重叠式的平坦社区检测算法. 两者都与节点嵌入任务联合建模, 前者基于重叠的高斯分布假设, 后者基于非负矩阵分解.

HCDE^[10]和LouvainNE^[9]: 非重叠式的层次社区检测算法. HCDE预先用图学习算法, 例如LINE^[14], 获得节点的嵌入表示, 再自顶向下地用启发式的策略构建节点-社区隶属关系. LouvainNE自顶向下递归地利用Louvain^[11]算法进行层次化社区构建, 随后再根据社区树单独学习节点的嵌入表示.

为了观察先验知识扰动对我们模型的影响, 我们分别设计了Ours-Wide, Ours-Deep和 Ours-Comb. 3种基于广度树, 深度树和组合树的重叠式层次社区检测算法, 仅社区层次结构的表达形式不一致.

我们用以下两组指标来评估模型在社区检测任务和节点嵌入下游任务的表现:

Modularity: 评估得到的节点-社区隶属关系是否符合社区检测任务模块化的要求. 它的值越高, 就意味着越多有密集关联的节点被分配到同一社区当中, 社区检测的结果越好.

AUC: 为评估节点嵌入表示在下游链路预测任务上的表现力, 我们通过嵌入表示计算成对节点的相似度, 并映射到[0,1]区间内, 结合多种阈值设定和成对节点的真实标签计算AUC的值, 该值越高意味着预测结果越准确.

此外, 我们对层次社区结构进行可视化展示, 以证明我们模型的层次结构建模能力.

3.2 实验结果

我们按照7:1:2的比例划分了训练、验证和测试数据集, 并以正样本两倍的数量随机采样负样本, 采用10-fold交叉验证的方式来确定最优参数. 我们定义社区数量在15–20之间, 训练过程中使用学习率为0.003的Adma优化器^[16]. 表1展示了4组模型在社区检测任务和链路预测任务上的结果.

我们首先根据4组模型的社区检测结果来考量这些社区的模块化程度: (1)重叠式平坦模型ComE和MNMF的模块化程度整体上是高于非重叠模型SCD和vGraph的, 这表明了重叠社区建模的优势;(2)非重叠层次模型HCDE和LouvainNE的效果持平或略差于SCD和vGraph, 这是因为没有利用图表示学习进行双任务联合优化, 因此效果略差; (3)我们的3种重叠式层次社区检测算法在两组数据集上的结果均优于基线模型, 这也进一步说明了层次社区结构和重叠社区分布的合理性.

其次, 我们需要验证节点嵌入表示在下游链路预测任务上竞争力: (1)重叠式平坦模型MNMF的AUC值高于非重叠模型vGraph, 这表明了重叠式社区分布假设的优势. ComE的值没有竞争力是因为模型侧重于社区建模, SCD没有节点嵌入表示学习建模的部分; (2)非重叠层次模型HCDE和LouvainNE的效果与vGraph持平或更差, 其原因是启发式算法节点嵌入表示和社区检测分离的优化方式竞争力不足; (3)我们的模型与所有基线模型相比同样具有强劲的竞争力, 这证明了重叠式层次社区分布假设的合理性, 以及节点嵌入和社区检测双任务可以达到双赢的效果.

此外, 我们发现在基于不同形态的层次结构时, 不论是纯粹的深度树(deep)还是广度树(wide)其社区模块化程度和下游任务效果都没有深广度组合树(Comb.)好, 这意味着一份数据集内不同的社区可被细分的粒度是不一致的, 有些倾向于细分为多类, 有些倾向于细分为更多的层次, 这是一种合理的现象.

3.3 社区分布可视化展示

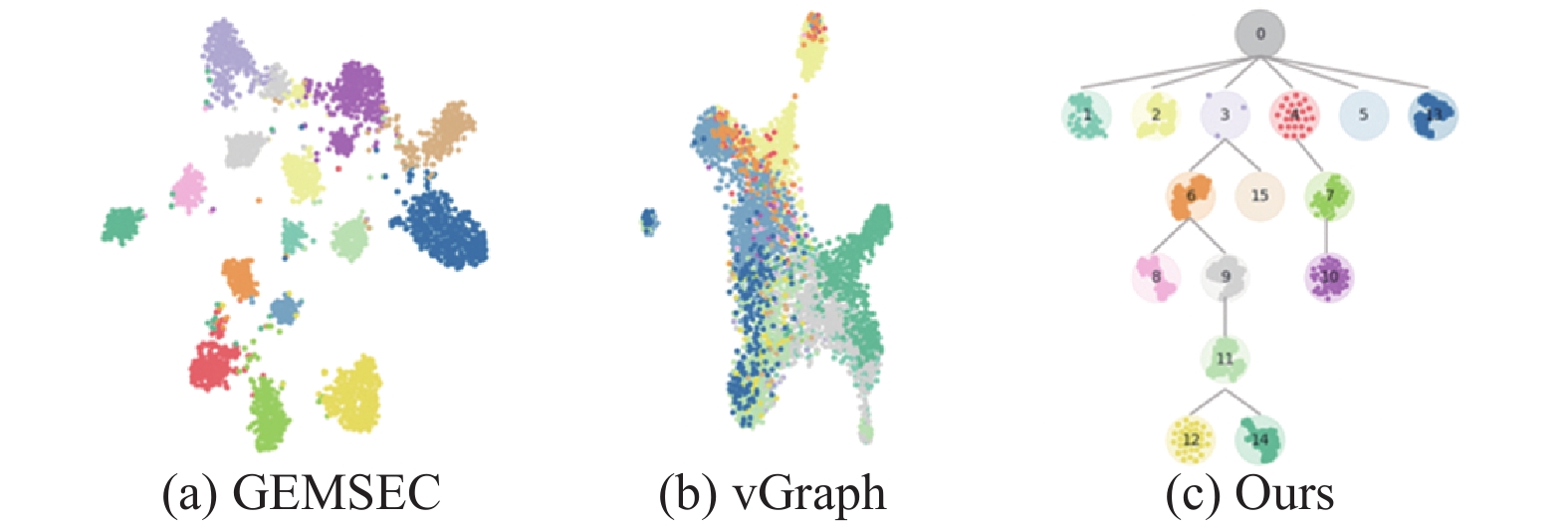
我们利用t-SNE技术^[17]将节点的嵌入表示从高维空间映射到二维空间. 以假设存在15个社区的Aminer数据集为例, 为属于同社区的节点赋予相同的颜色进行可视化展示. 图3展示了基线算法和我们的社区树. 这3个模型的社区模块化程度都较高, 相同颜色的点都比较聚集. 但我们的模型学习出了基于任意层次结构模型的节点-社区隶属关系分布.

4 结论与展望

本文提出了一种基于梯度的重叠式层次社区检测算法, 在层次结构未知的情况下, 通过梯度更新的方式联合优化节点嵌入表示和社区检测任务, 灵活地探索节点和重叠式层次社区的隶属关系. 我们提供了多样化的实验结果以及社区树的可视化形态, 均证明了该算法的有效性. 接下来, 我们将考虑如何利用基于梯度的优化方式和强化学习等技术, 帮助模型自动探索层次结构, 不必受到获取先验知识的成本约束.