推荐系统能够帮助用户从浩繁的信息快捷地选出他们感兴趣的内容, 但是我们面临一个重要问题是用户的兴趣会随着时间发生变化[1,2], 此外新用户也会不断到来. 根据最新的调研, 电商平台的销售量和其推荐服务对用户的响应性呈现显著的正相关关系[3]. 在这样的背景下, 我们提出响应性作为一个在线推荐系统需要满足的重要指标. 具体来说, 当系统收集到用户少量的最新交互信息之后, 一个响应式推荐系统需要满足如下需求:
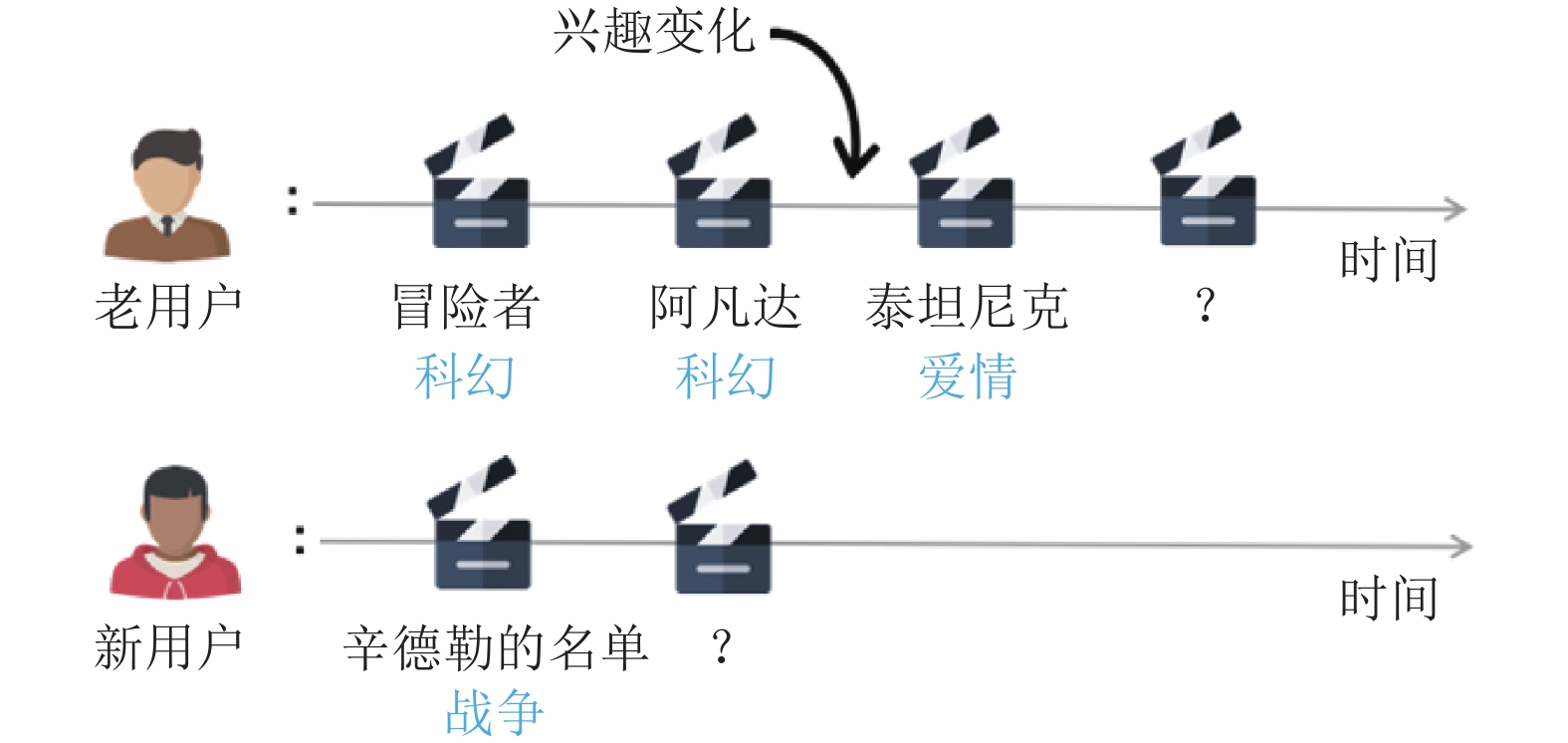
(1) 对老用户的响应性. 响应式推荐系统需要及时有效地捕捉到老用户兴趣的变化. 以图1中的上半部分为例, 对于一个老用户, 他之前都是比较喜欢科幻类型的电影. 但是最近, 该用户的兴趣发生了变化, 展现出了对情感类型电影的兴趣. 这种变化可能是受朋友影响或者个人经历变化等因素.
|
图 1 两个典型的响应式推荐系统需求场景示意图 |
(2) 对新用户地响应性. 响应式推荐系统需要准确地学习新用户兴趣. 以图1中下半部分所示为例, 该用户为系统中新用户且只有只看了一部战争类型地电影.
接下来, 我们将这两点响应性需求统称为学习用户近期的兴趣. 根据我们的调研, 尽管响应性是推荐系统中一个重要的需求, 现有的方法还没有很好地满足该需求. 一方面, 传统的推荐系统方法采用线下训练线上预测的模式[4,5]. 这些方法很难满足响应性的需求, 因为模型训练好之后就不再改变. 重新训练模型又十分耗时难以满足时间需求. 另一方面, 最近的一些研究工作提出了一些增量更新的在线推荐算法[1,6-10]. 相比于重新训练模型, 这些方法很好地提升了模型更新的时间效率. 这些方法主要分为两类, 一类是在线下训练好的模型的基础上, 只使用新的交互信息微调(fine-tuning)模型[8-10];另一类方法会缓存一部分交互信息到一个池子(reservoir)中, 然后定时更新模型, 更新模型是使用池子中的交互信息和新的交互信息同时微调模型[1,7].
虽然这些基于微调的更新方法可以解决模型更新的时间效率问题, 他们面临着新的交互信息量太少的问题. 传统的机器学习模型需要大量的数据才能准确学习样本的表征, 以 MNIST 手写数字识别数据集为例, 该数据集有 6 万张图片, 平均每个数字有 6 千张图片. 为了应对新的交互信息量太少的问题, 我们提出了一套基于元学习[11]的增量式模型更新方案. 该方案能够从之前的利用大量的历史交互数据训练的过程中, 学习出一些解决训练数据量少问题的先验知识, 然后我们将这些先验知识应用于最近的利用少量新的交互信息的更新过程中, 从而指导模型更好地学习用户近期的兴趣.
元学习在许多小样本学习(few shot learning)的任务中都取得了超过了微调的方法[11-13]. 其设计理念借鉴于人类的学习过程. 人类在学习新的种类的分类任务时, 往往只需要一两张样例图片就可以了, 这是因为人类在分类未见过的种类时, 会使用到之前学习到的先验知识, 而不是像传统的机器学习算法一样从头开始学习.
从元学习的角度看, 在我们的推荐场景中, 响应式推荐的要求是根据某个用户少量的最新的交互信息为其推荐下一个物品. 我们将这个需求定义为一个任务. 为了能够利用少量的样本学习出用户在新交互物品上的兴趣. 借鉴于元学习的思想, 我们需要为该任务准备先验知识. 接下来的问题是要如何学习这样的先验知识. 为了学习先验知识, 我们首先利用大量的历史交互数据构建与当前任务相似的任务, 即使用用户相连的少量交互去预测紧接着的下一个交互. 从历史数据中, 我们可以构建大量的这样的任务. 然后我们使用模型的初始参数作为先验知识. 该初始参数能够使得模型在该任务上仅使用少量的样本就能准确学习出用户近期的兴趣. 为了学习到这样的初始参数, 借鉴于元学习的想法, 我们将该需求建模成线下训练过程中监督损失函数, 即线下训练的任务要在使用该初始参数的基础上, 经过少量交互的更新, 都能准确预测其任务中对应的下一个交互物品. 这样, 在新的任务中, 模型就可以在之前的相似任务中学习到的初始参数的基础上更好地学习出用户的兴趣.
从传统方法的角度看, 相比于传统的线下训练好模型然后线上微调模型的策略. 我们的方法的优势是在线下训练模型的时候考虑到了之后线上更新只会有少量的交互信息, 并将其设计在了线下更新模型参数的损失函数中. 这样学习到的模型参数能够在线上更新的过程中仅使用少量的新的交互信息就能更准确地学习出用户近期的兴趣.
后文组织如下: 第1节介绍我们提出的基于元学习的响应式推荐算法; 第2节介绍实验设置和实验结果分析; 第3节进行总结和展望未来工作.
1 基于元学习的响应式推荐系统 1.1 构建线下训练任务我们将
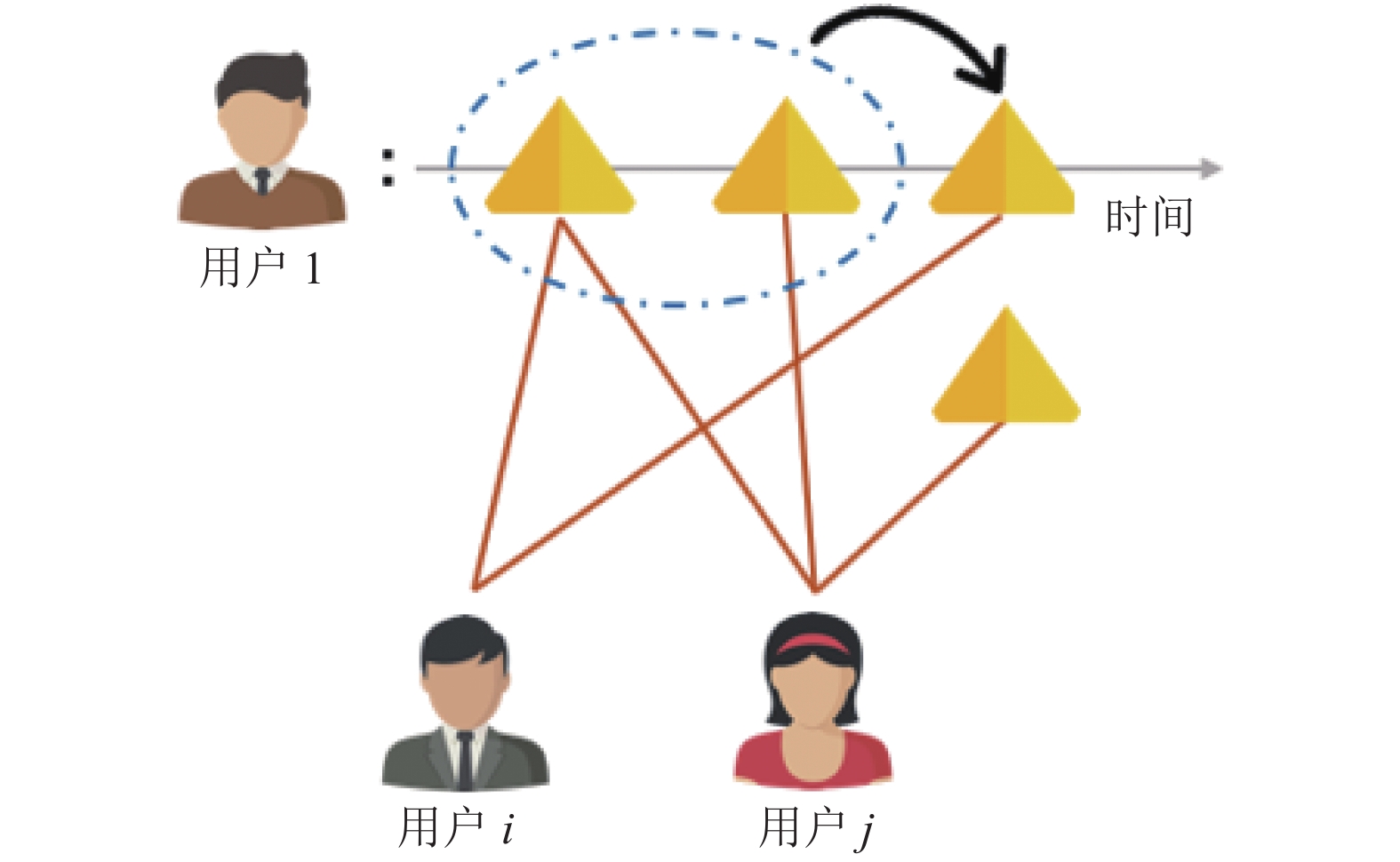
|
图 2 一个带有邻居信息的线下训练任务 |
1.2 利用元学习提取先验知识
我们将推荐模型记为f, 所有任务共享相同的推荐模型结构, 然后在自己的任务上调整其参数以满足任务需求. 借鉴于 MAML[11] 的想法, 我们将先验知识定义为模型f的初始参数, 记为
| $ {\varTheta }_{t}=\varTheta -{α}{\nabla }_{\varTheta }{{L}}_{{t}}^{{K}}\left(\varTheta \right)$ |
其中,
| $\mathop {{\rm{min}}}\limits_\varTheta \mathop \sum \limits_t L_t^1\left( {{\varTheta _t}} \right) = \mathop {\min }\limits_\varTheta \mathop \sum \limits_t L_t^1\left( {\varTheta {\rm{ = \alpha }}{\nabla _\varTheta }{{L}}_{{t}}^{{K}}\left( \varTheta \right)} \right)$ |
其中,
在我们的场景中, 我们使用矩阵分解模型[3]来实现推荐模型f, 模型的参数
然后我们基于BPR (Bayesian Personalized Ranking)[14]的方法来设计优化目标
| ${D_R} = \left\{ {\left( {{u_i},{v_j}} \right)\left| {\left( {{u_i},{v_j}} \right)} \right. \in R \cap \left( {{u_i},{v_k}} \right) \notin R} \right\} $ |
然后结合矩阵分解给出的评分, 对于用户
| ${\hat x_{ijk}} = {{{r}}_{{{ij}}}} - {r_{ik}} = p_i^{\rm{T}}{q_j} - p_i^{\rm{T}}{q_k}$ |
因为我们需要将交互过的物品排在为交互过的物品之前, 所以需要最大化
| ${{{L}}_{{{ijk}}}} = - \log \sigma \left( {{{\hat x}_{ijk}}} \right) + {\lambda _P}{\left| {\left| {{p_{\rm{i}}}} \right|} \right|^2} + \lambda _Q^ + {\left| {\left| {{q_j}} \right|} \right|^2} + \lambda _Q^ - {\left| {\left| {{q_k}} \right|} \right|^2}$ |
其中,
有了 BPR 损失函数的定义之后, 对于某个任务
| ${{L}}_{{t}}^{{T}} = \mathop \sum \limits_{({u_i},{v_j},{v_{k) \in {D_{R_t^K}}}}} {L_{ijk}}$ |
其中,
值得注意的是在任务t上经过L次更新之后得到的参数, 记为
| $\mathop {{\rm{min}}}\limits_\varTheta \mathop \sum \limits_t L_t^K\left( \varTheta \right) + {\lambda _{\rm ML}}L_t^1\left( {\varTheta _{{t}}^{{L}}} \right)$ |
其中,
学好了先验知识
最后, 我们的模型非常容扩展线上增量更新. 给定一个新的交互(u, v), 如果用户u或者物品v是新用户或新物品, 我们照如下公式初始化他们的特征:
| $ {p}_{{M}+1}=\frac{1}{M} \sum \limits_{{{u}}_{{m}}\in U}{p}_{m}+{\epsilon}_{p}$ |
| $ {q}_{{N}+1}=\frac{1}{N} \sum \limits_{{v}_{n} \in V}{q}_{n}+{\epsilon}_{q}$ |
其中, U和V表示现有用户和物品的集合; M和N是现有用户和物品的数目;
如果用户u不是新用户, 则我们可以为该新交互构建一个任务, 其中待预测交互集合
我们使用了MovieLens-1M和Netflix这两个公开数据集做了验证实验. 两个数据集都是电影评分数据集. 其中, MovieLens-1M数据集大约包含6千用户, 4千部电影和1百万个评分, 后面简称MovieLens; Netflix数据集大约包含1.8万用户, 45万部电影和1亿个评分. 评分的范围是从1到5. 所有的评分都有一个时间戳. 在我们的实验中, 类似于BPR[14] 的设置, 我们将评分大于等于3的电影视为正样本, 其它的都视为为交互过的样本.
2.2 对比模型介绍我们选取如下流行的线上推荐模型作为对比:
(1) RKMF[5]: 该方法使用核函数建模用户与物品特征向量间的关系. 在迭代更新的过程中, 该方法交替地更新用户特征或者物品特征.
(2) sRec[9]: 该方法使用概率模型建模用户特征和物品特征的演变过程, 并且使用现有特征来初始化新用户或者新物品特征.
(3) SPMF[10]: 该方法在迭代增量的更新过程中, 同时会使用缓存的之前的一部分老的交互信息.
2.3 评估方法介绍我们首先随机选出10%的用户作为新用户, 将他们的交互信息从数据集中移除. 为了验证推荐模型的响应性, 对于这些新用户, 我们为模型提供这些用户的 n 个新的交互, 然后检测模型是否能够准确预测这些用户的下一个交互. 在实验中, 设置n = 1, 5, 10 三种情况.
然后我们将剩下的交互信息按照时间顺序划分为90%和10%两部分. 对于所有的模型, 我们将90%的部分用于线下训练模型, 然后后面10%的部分用于线上迭代更新模型并检验模型对于老用户兴趣变化的响应性. 在这个过程中, 对于后面10%的交互信息, 按照时间顺序, 每当来一批交互信息的时候, 我们先验证模型是否能够准确预测这些交互信息, 然后再用这些新的交互信息更新模型.
根据之前的工作, 我们采取 leave-one-out 的评估模式[16,17]. 我们的目标是预测用户的下一个交互的物品, 为了评估模型同时提升评估效率, 我们从为交互过的物品中随机采样100个物品作为负样本. 然后我们根据模型对这101个物品的评分计算如下3个评测指标:
(1) HR@K(Hit Ratio): 评估正样本出现在排序前K个之中的比例.
(2) AUC: ROC曲线下的面积值. 简单来说, 该方法综合评估了正样本排在负样本前面的概率.
(3) NDCG@K (Normalized Discounted Cumulative Gain): 该方法要求正样本排在前K个的同时还会根据排序位置进行惩罚. 排序越靠后, 惩罚越多.
总的来说, 这3个指标都是得分越高, 模型性能越好.
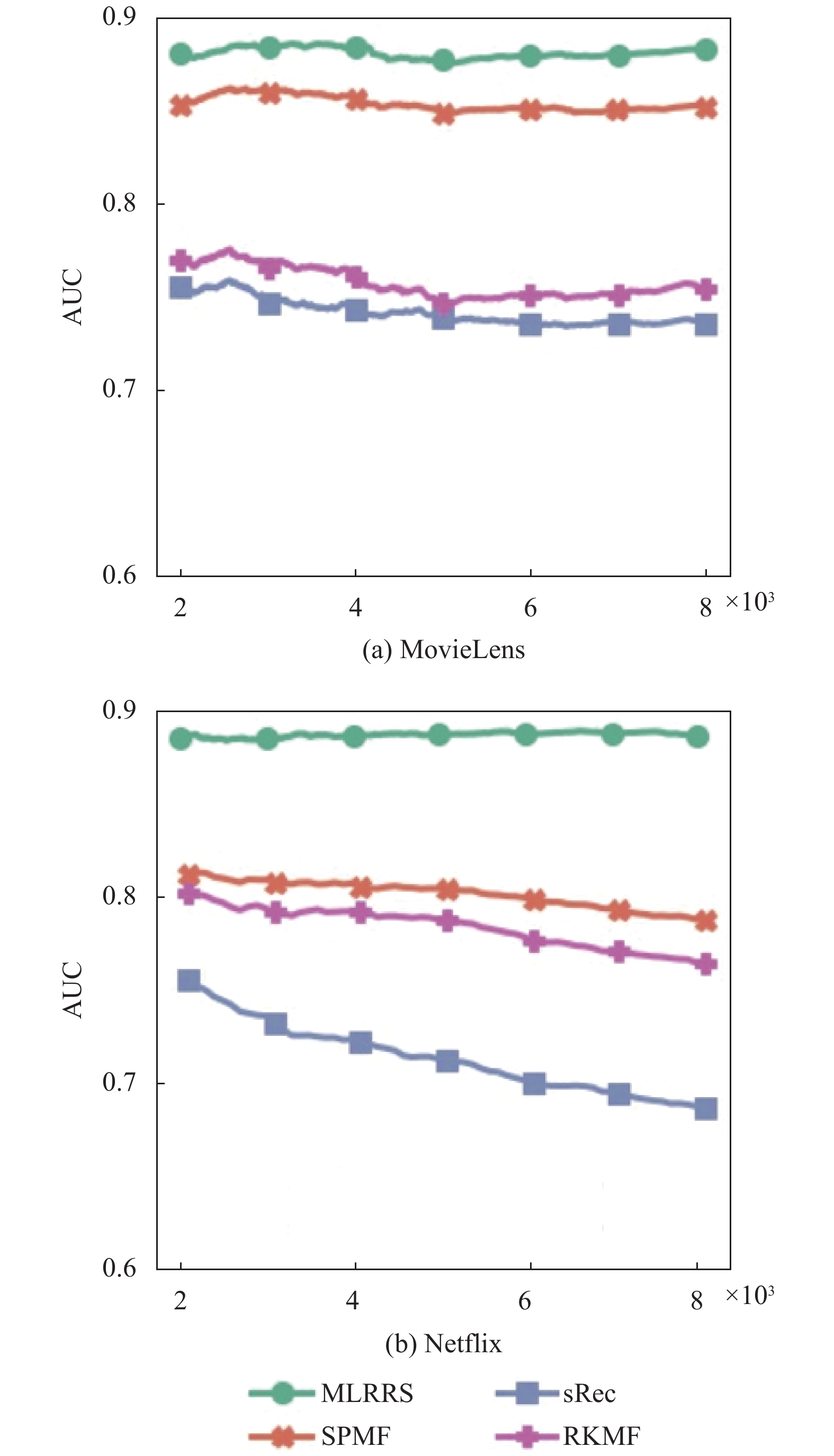
2.4 对老用户的响应性对比图3展示了不同模型在更新更新过程中的性能变化曲线. 从图中可以看出, RKMF和sRec模型的性能在线上更新的过程中迅速下降. 因为这些模型在线上更新的过程中忽略了历史数据, 从而导致模型在少量新样本上容易过拟合, 出现模型不稳定现象. 与之不同, 我们的模型在自己相对独立的任务中, 基于共有的先验知识, 独立地优化自己的参数, 导致模型不会受到少量新交互信息的剧烈扰动, 从而表现出更高的稳定性. 同时, 由于使用的历史信息的先验知识更利于模型在少量样本上快速收敛, 我们的模型在响应式推荐的任务中性能表现也更好.
2.5 对新用户的响应性对比表1展示了不同模型在学习新用户兴趣任务上的表现, 其中n为模型当前观测到的新用户的交互的数量. 从表中可以看出我们的模型在学习新用户兴趣上的显著优势. 举例来说, 在Netflix数据集上, 当n = 1时, 我们的模型在NDCG@10的指标上超出了对比模型13%.
|
图 3 不同模型对老用户响应性的 AUC 值对比 |
| 表 1 不同模型对新用户响应性对比(HR@10 和 NDCG@10简记为 HR 和 NDCG) |
此外, 相对于HR@10评价指标, 我们的模型在NDCG@10评价指标上取得了更高的提升. 举例来说, 在 MovieLens数据集上, 当n = 5的时候, 我们的模型在HR@10指标上取得了10.7%的提升, 在NDCG@10指标上取得了13.4%的提升. 在Netflix的数据集上也有相同的现象. 由于NDCG指标会对排序位置进行惩罚, 这说明了我们的模型可以将正样本排得更靠前.
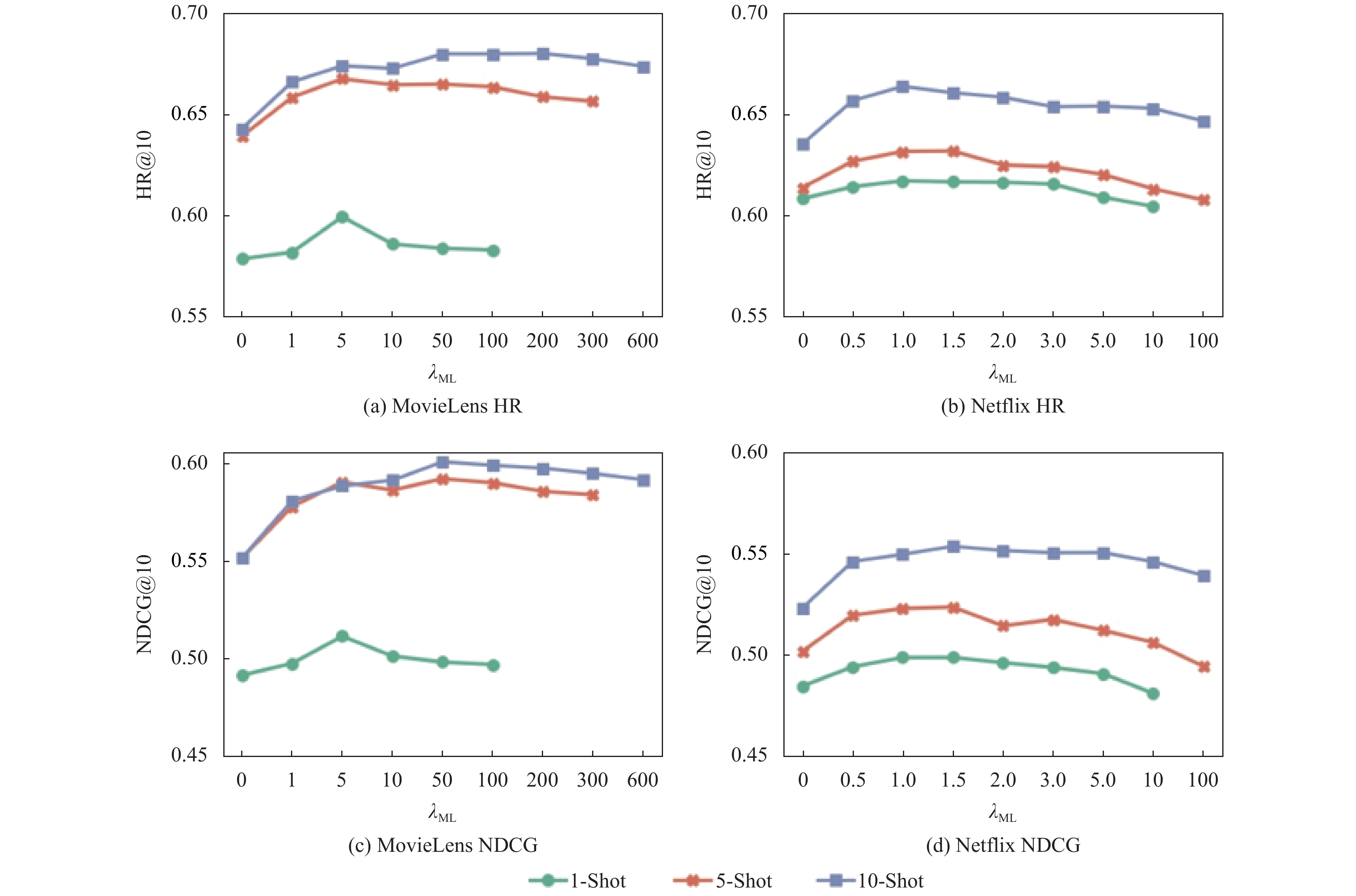
2.6 对元学习损失函数权重的实验分析我们细化研究了元学习损失函数对我们模型性能的影响. 图4展示了实验结果, 从图中我们我们可以分析得出如下结论:
(1)使用适当的权重, 我们的元学习损失函数能够使得模型学习出更好的性能
(2)随着元学习损失函数权重
|
图 4 元学习损失函数权重
|
3 结论和展望
在本文中, 我们提出了一套基于元学习的响应式在线推荐系统设计. 在线上更新的过程中, 由于新的交互信息数量少, 导致模型很难根据少量新的交互信息准确快速地学习出用户最近的兴趣. 在我们的方法中, 我们通过基于元学习的方案, 从大量的历史交互信息中提取出先验知识, 然后使用该先验知识指导模型的线上更新过程, 从而使得模型能够更加准确地学习出用户最近的兴趣. 我们通过大量的实验证明了我们方案的有效性.
在未来的工作中, 我考虑使用社交网络的信息来增强对用户兴趣特征的建模[18-20]; 同时我们希望通过元学习的方法更加细致地建模分析用户的兴趣随时间变化的模式.
| [1] |
Chen H. Modeling and detecting drift in user interest based on hierarchical classification. Proceedings of the 2019 IEEE 4th International Conference on Big Data Analytics. Suzhou, China. 2019. 246–251.
|
| [2] |
Wang WQ, Yin HZ, Huang Z, et al. Streaming ranking based recommender systems. Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor, MI, USA. 2018. 525–534.
|
| [3] |
Chavosh A, Halimi A B, Soheilirad S, et al. Customer responsiveness and export performance of selected electronic equipment export companies in malaysia. Proceedings of 2011 International Conference on Social Science and Humanity-Section1. Singapore. 2011. 124–127.
|
| [4] |
Koren Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas, NV, USA. 2008. 426–434.
|
| [5] |
Salakhutdinov R, Mnih A. Probabilistic matrix factorization. Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver, BC, Canada. 2007. 1257–1264.
|
| [6] |
Rendle S, Schmidt-Thieme L. Online-updating regularized kernel matrix factorization models for large-scale recommender systems. Proceedings of the 2008 ACM Conference on Recommender Systems. Lausanne, Swiss. 2008. 251–258.
|
| [7] |
Diaz-Aviles E, Drumond L, Schmidt-Thieme L, et al. Real-time top-n recommendation in social streams. Proceedings of the 6th ACM Conference on Recommender Systems. Dublin, Ireland. 2012. 59–66.
|
| [8] |
Song Q, Cheng J, Lu HQ. Incremental matrix factorization via feature space re-learning for recommender system. Proceedings of the 9th ACM Conference on Recommender Systems. Vienna, Austria. 2015. 277–280.
|
| [9] |
He XN, Zhang HW, Kan MY, et al. Fast matrix factorization for online recommendation with implicit feedback. Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval. Pisa, Italy. 2016. 549–558.
|
| [10] |
Chang SY, Zhang Y, Tang JL, et al. Streaming recommender systems. Proceedings of the 26th International Conference on World Wide Web. Perth, France. 2017. 381–389.
|
| [11] |
Finn C, Abbeel P, Le S. Model-agnostic meta-learning for fast adaptation of deep networks. Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia. 2017. 1126–1135.
|
| [12] |
Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain. 2016. 3637–3645.
|
| [13] |
Yoon J, Kim T, Dia O, et al. Bayesian model-agnostic meta-learning. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montreal, QC, Canada. 2018. 7343–7353.
|
| [14] |
Rendle S, Freudenthaler C, Gantner Z, et al. Bpr: Bayesian personalized ranking from implicit feedback. Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence. Montreal, QC, Canada. 2009. 452–461.
|
| [15] |
Pascanu R, Mikolov T, Bengio Y. Understanding the exploding gradient problem. arXiv: 1211.5063.
|
| [16] |
Huang J, Zhao WX, Dou HJ, et al. Improving sequential recommendation with knowledge-enhanced memory networks. Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor, MI, USA. 2018. 505–514.
|
| [17] |
Cao D, He XN, Miao LH, et al. Attentive group recommendation. Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor, MI, USA. 2018. 645–654.
|
| [18] |
Li XQ, Yan XM. Analyzing of personalized recommendation model of social network users based on big data. Proceedings of the 2019 6th International Conference on Dependable Systems and Their Applications. Harbin, China. 2020. 135–142.
|
| [19] |
Guo YN, Cao JX, Lin WG. Social network influence analysis. Proceedings of the 2019 6th International Conference on Dependable Systems and Their Applications. 2020. Harbin, China. 517–518.
|
| [20] |
Firdaus MF, Baizal ZKA, Bratawisnu MK, et al. Pattern recognition of dynamic social network. Proceedings of the 2020 3rd International Conference on Intelligent Autonomous Systems. Singapore. 2020. 56–61.
|
 2021, Vol. 30
2021, Vol. 30



