2. 肇庆学院, 肇庆 526061
2. Zhaoqing University, Zhaoqing 526061, China
信息化时代, 校园一卡通已成为校园信息化建设的重要支撑部分. 它既能反映校园信息化建设的有效性, 又能改善学校管理和服务, 为广大师生带来便利. 一卡通管理系统收集了大量数据, 涵盖了诸如食堂或超市消费、学生考勤、教师考勤与会议出勤、各种门禁、图书借阅、热水和饮用水等多个领域. 近年来, 这些数据倍受关注, 特别是众多学者开始高度重视各种领域的时间序列预测研究, 基于大数据方法的研究与应用前景广阔[1,2]. 本文以某学校教师和学生在食堂消费的交易数据为研究对象, 通过对消费数据分析和预测的研究, 挖掘出学校食堂消费的变化规律和未来发展趋势, 并提供较为准确的预测, 给学校后勤部门提供了参考意见. 这将有助于学校的建设和管理. 特别是管理食堂的学校后勤部门可据此加强管理, 更好地满足广大师生的消费需求. 研读了大量的相关文献, 大数据挖掘和分析应用领域广泛, 结合迁移学习方法可以更好地预测气象因子时间序列的变化趋势[3], 多时间尺度时间序列趋势预测算法可对股票、基金等未来变化进行预测[4]. 学习了前人做过的一些分析方法和实例[5-8], 认为食堂消费数据是平稳的单序列, 适合用ARIMA模型拟合与预测[9,10]. 但ARIMA只能建立线性的模型, 而现实世界中用纯线性模型拟合很难达到实验预期要求, 由于学校食堂消费行为和假期密切相关, 有明确周期性的特点, 又可考虑Holt-Winters方法[11,12]. 本实验分别使用了这两种方法, 而拟合和预测的结果通过检验、对比, 发现Holt-Winters预测的精度更高, 是更优的方案.
1 数据预处理首先收集原始数据, 进行数据预处理, 目的是把未加工的数据转换成适合挖掘处理的形式, 然后进行拟合分析, 最后做出预测并检验结果的准确性[13]. 数据挖掘, 是指从海量的数据中通过一定的算法发现人们有兴趣的信息的过程. 为了提高数据的质量, 为下一步的分析提供有效及可用的数据, 需要进行数据预处理. 数据噪声是原始数据的各个变量的随机误差或方差, 可以使用移动平均法、指数平滑法等方法来消除之, 更真实地反映出时间序列的发展趋势. 时间序列的短期预测方法有很多, 其基本思想为: 消除一些不规则变化, 得到时间序列一些基本的变化模式, 然后按照此变化模式向后展开. 因此在数据预处理阶段, 消除一卡通数据中那些随时间的不规则变化, 把它的基本变化模式更显著地描述出来是很有必要的.
1.1 数据清理数据清理, 就是清除一卡通数据中的噪声, 去除与研究无关的因素. 校园一卡通系统中的数据主要是由教师、学生, 还有少量的工人、教师家属和社会人士刷卡产生. 为了保证研究数据的可靠性和稳定性, 要根据需求, 针对性地研究教师和学生这个主体对象, 而把少量的其他人随机性的刷卡数据清理掉, 以免影响实验效果. 目前, 某校一卡通建设还处于初级阶段, 校园卡主要用途暂时为食堂消费. 初步统计结果发现一个教工食堂和两个学生食堂消费占约94.8%, 其他的消费则发生在学校小卖部、饮用水和热水等, 数据清理容易实现. 研究针对相对平稳的、全部食堂总的交易笔数组成的时间序列, 当然, 今后也可以对消费金额进行研究.
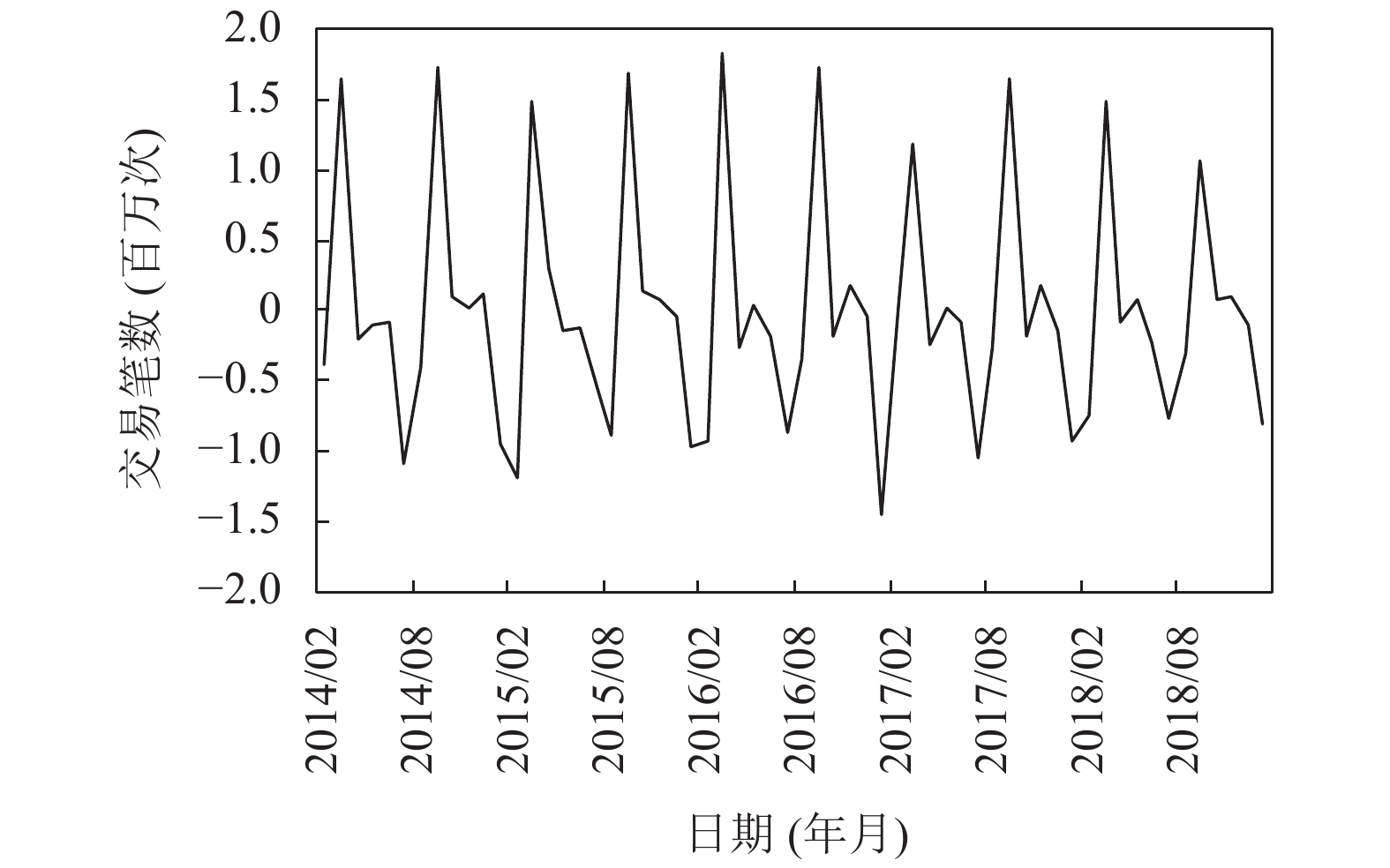
1.2 数据平滑一卡通系统导出的数据是不平滑的, 这对变化曲线的拟合来说就有影响. 有的噪声数据会影响拟合函数的准确性, 在对时间序列变化趋势的曲线进行拟合前, 应该进行平滑处理. 受周期变动和随机波动的影响, 全部食堂逐年的月消费总笔数随时间变化的起伏较大, 给揭示时间序列发展趋势带来困难, 而使用Holt-Winters和ARIMA方法就能解决这个问题. 这两种方法对含有线性趋势和周期波动的非平稳序列适用, 而且利用指数平滑法(EMA)能让模型参数不断适应非平稳序列的变化, 并对未来趋势进行短期预报. 首先观察原始序列变化趋势图, 如图1所示.

|
图 1 食堂消费数据之原始时间序列的变化趋势 |
为了对数据序列进行平稳性分析, 将非平稳性数据处理成平稳性数据, 然后建立最优食堂逐年的月交易量预测模型, 最后将预测值与实际交易量进行对比, 检验预测效果. 时间序列经平滑处理后的变化趋势如图2所示, 此时已能看出变化趋势存在显著的季节性.
2 数据分析 2.1 初步分析统计样本为学校的食堂在节假日与工作日期间使用一卡通消费的情况, 根据平滑后的曲线进行初步分析, 消费变化趋势可以粗略地归纳如下:
|
图 2 食堂消费数据之平滑后的时间序列变化趋势 |
(1) 从食堂节假日刷卡情况与工作日刷卡情况对比来看, 两个期间交易次数明显不同, 前者交易次数明显少于后者交易次数.
(2) 节假日期间, 特别是寒、暑假, 由于在校师生明显减少, 在学校食堂消费行为也大幅下降没有存在明显的刷卡消费峰值, 说明被研究的时间序列具有显著的季节性特点.
(3) 自2017年开始食堂消费交易次数有减少的趋势, 这和学校因某项目工作的需要而减少招生规模有密切关系.
2.2 模型的选择统计样本为学校的食堂在节假日与工作日期间使用一卡通消费的情况, 根据平滑后的曲线进行初步分析, 消费变化趋势可以粗略地归纳如下:
首先考虑使用ARIMA模型. ARIMA是Autoregressive Integrated Moving Average Model的缩写, 称为自回归滑动平均模型. 该模型特点是不直接考虑其他相关随机变量的变化. 既带有趋势又有季节性趋势的模型为ARIMA(p, d, q)×(P, D, Q)S. 其中的非季节性参数p, d, q和季节参数P、D、Q将在后面的分析中确定, 而S为时间序列的周期, 这里选年周期, 12个月, 即S=12. 但ARIMA只能建立线性的模型, 而纯线性模型在现实世界中还是少见的, 用ARIMA模型来分析有时会达不到预期效果. 初步实验, 通过差分与季节差分运算去除时间序列的趋势与季节成分, 将原序列平稳化. 用条件最小二乘法进行参数估计, 并进行显著性检验[14], 发现此模型拟合变化曲线的效果不是很好. 模型的评估有两种准则, 分别是赤池信息准则(AkaikeInformation Criterion, AIC)和贝叶斯信息准则(Bayesian Information Criterion, BIC), 这里使用BIC准则. 根据非季节性参数p, d, q和季节参数P、D、Q多种不同的组合中选取BIC的值最小的组合. 最后得到模型为ARIMA(1,1,2)(0,1,0), 平稳的R方为0.725, BIC为25. 平稳的R方主要用于测定线性回归的拟合度, 取值范围为0<│R│≤1. R越大, 因变量与解释变量间的线性关系越显著[15]. 预测结果如表1所示. 建立95%的预测区间, 表中的UCL为预测上限, LCL为预测下限.
| 表 1 基于ARIMA模型的食堂消费之交易笔数预测效果 |
由表1可见, 3、4、5三个月的相对误差增长很快, 5月的预测值相对误差超过了10%, 后续预测不可靠, 实验效果没有符合预期. 于是改用Holt-Winters乘法模型, 经过3次指数平滑实验, 可发现拟合和预测的效果会更好. Holt-Winters在两参数指数平滑的基础上, 引入第3个参数处理数据季节性, 也称为三阶指数平滑[16]. 三参数指数平滑模型本质上是一种高级指数平滑模型, 可同时处理趋势和季节性变化, 可适当地过滤随机波动的影响, 对兼有长期趋势和季节模式的数据进行预测.
2.3 结果检验、对比与分析统计样本为学校的食堂在节假日与工作日期间使用一卡通消费的情况, 根据平滑后的曲线进行初步分析, 消费变化趋势可以粗略地归纳如下:
建模过程是一个不断优化、不断改进的过程, 没有绝对的标准答案, 而是最终取尽量好的结果. Holt-Winters算法也叫三次指数平滑算法, 是在一次指数平滑、二次指数平滑算法基础上改进的, 它适用于预测具有趋势性和季节性的时间序列, 有加法模型和乘法模型两种[17], 当季节性变化相对稳定时一般使用加法模型, 当季节性变化呈现比例变化特点时一般使用乘法模型[18]. 这里选择了Holt-Winters乘法模型, 可从长期趋势、周期两个方面进行分析. 乘法模型公式如下:
| ${L_t} = \alpha ({Y_t}/{S_{t - 1}}) + (1 - \alpha )({L_{t - 1}} + {T_{t - 1}})\;\;\;\;$ | (1) |
| ${T_t} = \beta ({L_t} - {L_{t - 1}}) + (1 - \beta ){T_{t - 1}}\;\;\;\;$ | (2) |
| ${S_t} = \gamma ({T_t}/{L_t}) + (1 - \gamma ){S_{t - p}}$ | (3) |
| ${F_{t + k}} = ({L_t} + k{T_t}){S_{t + k - p}}$ | (4) |
以上4个公式中, α为水平平滑系数, β为趋势平滑系数, γ为季节平滑系数, 它们大小介于0和1之间. Yt为t时刻的实际值, Lt为t时刻的水平值, Tt为t时刻的趋势值, St为t时刻的季节值, k为外推预测时期数, p为周期长度. 对2019年3月、4月和5月的食堂消费总交易笔数进行预测, 模型统计量如表2所示.
| 表 2 食堂消费Holt-Winters乘法模型的统计量 |
对结果检验可知该模型拟合中平稳的R方达到0.772, 高于0.5这个平均水平; 季节变动的整体R方为0.944, 接近1, 因此拟合效果还是很不错的. 最后看正态化的BIC值, 为24.133, 不算太大, 这进一步证明了该模型的拟合效果良好[19]. 方差分析结果通过F检验. F统计量的概率Sig值是显著性指标, 一般大于0.05拒绝原假设, 否则接受原假设. 本次实验结果, Sig的值为0.02, 小于0.05, 说明在显著性水平位, 可以使用该模型.
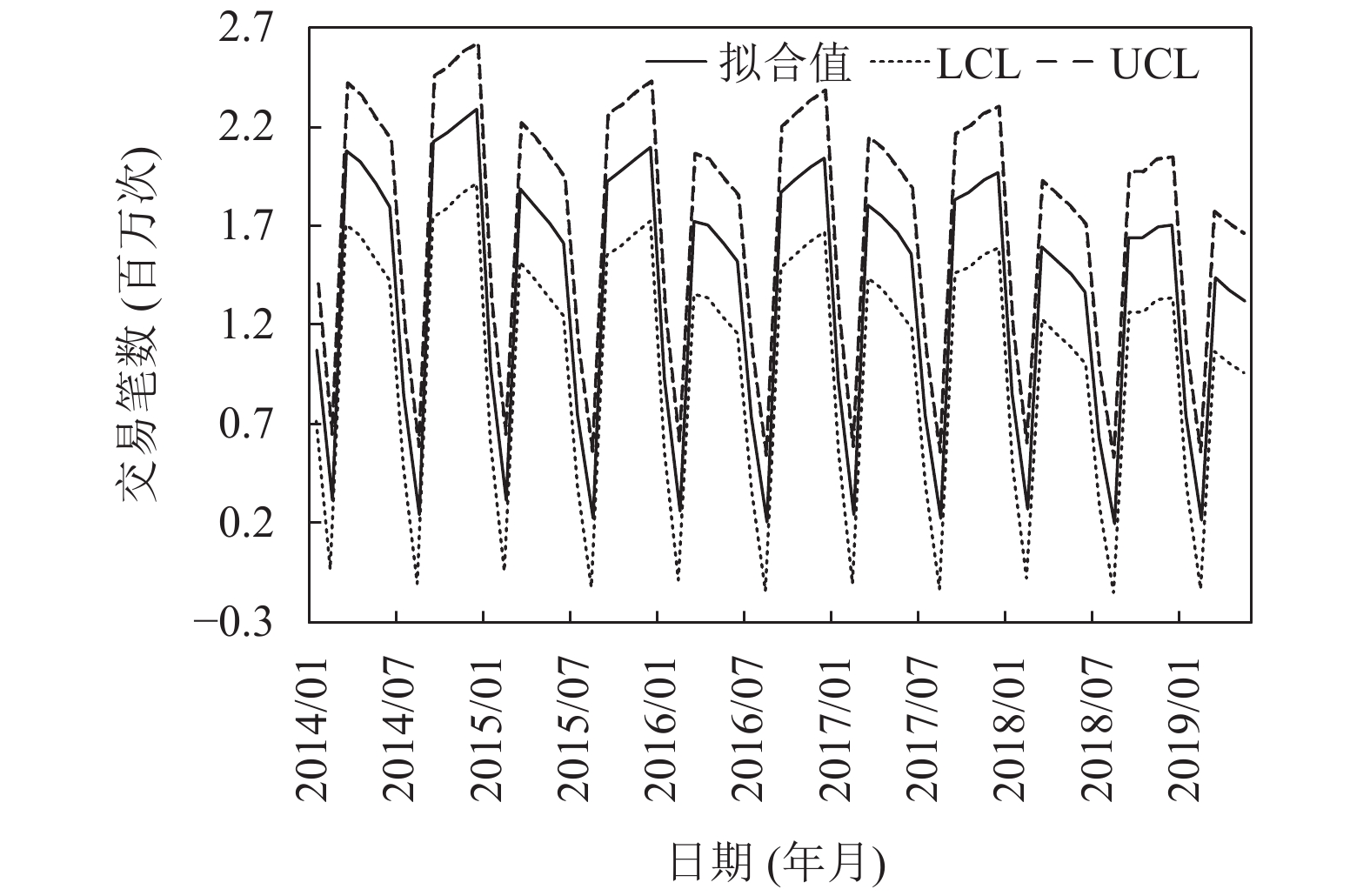
利用SPSS软件, 进行模型的建立和分析, 最后得到拟合和预测的效果图[20,21]. 先作拟合线和预测值95%的置信区间的上限和下限两条虚线, 如图3所示.
|
图 3 基于Holt-Winters乘法模型的拟合值在95%的置信区间的分布情况 |
图3中的细实线为一卡通系统数据库里记录的交易笔数实际值, 而粗实线则为Holt-Winters乘法模型的预测值, 两条虚线UCL和LCL分别为预测值95%的置信区间的上限和下限, 由图3可见拟合线在两条虚线划分的区域之内, 同样预测线也是如此.
拟合与预测效果见图4, 虚线为观测值, 实线为拟合线. 可见食堂消费交易笔数的变化是包含季节变动成分的, 同时还有减弱的趋势. 图4的右侧为对2019年3、4、5三个月的预测值和观测值的拟合情况, 效果很好.

|
图 4 基于Holt-Winters乘法模型的拟合与预测效果图 |
检验相对误差的结果如表3所示. 通过与实际数据对比, 计算出预测的相对误差均低于10%, 并且相对于表1, 实验效果得以改进, 预测准确度更高, 证明对这组食堂消费数据的分析中使用Holt-Winters乘法模型预测效果更好.
| 表 3 基于Holt-Winters乘法模型的食堂消费交易笔数预测效果 |
3 学校食堂管理重点和改进措施
由以上校园一卡通消费数据实验分析可知, 学校节假日与平时的消费习惯存在明显的差异[22,23], 建议学校相关管理部门可以根据持卡用户的消费习惯做出调整:
(1)在节假日期间, 食堂就餐刷卡交易次数较少, 可以通过适当停止个别食堂的营业, 缩小售饭区域, 轮休工作服务人员来达到节省开支的目的.
(2) 在节假日期间, 学生的消费习惯不统一, 营业档口可以相应调整营业时间, 并且可以根据学生在节假日的较高消费特点, 提供较平时更为高档的有特色的菜品吸引学生消费.
(3) 食堂在3月、9–12月刷卡消费频次较高, 应当提前准备充分的货源, 适当调整营业时间, 增加工作人员数量, 提升服务质量.
(4) 食堂刷卡消费长期看有减弱的趋势, 这和社会大环境有密切关系, 那么根据社会实际情况, 食堂应减少营业档口数, 减少食材的购买, 甚至暂时关停部分食堂. 而保持经营状态的食堂应结合实际情况, 保证饭菜色、香、味、形的同时, 适当增加花色品种, 以吸引消费者.
4 结论与展望以某学校食堂消费数据为研究对象, 对2014年1月至2019年2月的月交易笔数构成的时间序列进行平滑处理, 经过反复地实验, 分别利用ARIMA和Holt-Winters两种方法进行分析, 其拟合和预测的结果通过检验、对比, 最终构建了考虑季节性的Holt-Winters乘法模型, 取得较为理想的实验结果. 建设数字化校园是众多学校信息化建设的重要组成部分, 而校园一卡通的建设会促进数字化校园的发展. 深入挖掘分析一卡通业务里的消费数据对于分析师生的消费行为有着重要意义. 本次研究结果能够为相关管理部门提供学生校内真实可靠的消费行为, 用科学的方法研究食堂用卡消费水平与规律, 为学校的决策层在学校的发展上做出更为科学的判断. 今后, 随着一卡通建设的推进, 还可以继续研究门禁数据, 图书馆数据等, 揭示学生的行为规律, 为学校的管理提供参考.
| [1] |
李勃旭, 南西康, 郑向东, 等. 基于EMD-ARIMA模型的地铁门传动系统早期故障预测. 计算机系统应用, 2019, 28(9): 110-117. DOI:10.15888/j.cnki.csa.007090 |
| [2] |
夏杨, 王芳. 基于一卡通数据的校园大数据分析平台的构建与应用(自然科学版). 华中师范大学学报, 2017(S1): 146-151. |
| [3] |
Huang TW, Jiao F. Data transfer and extension for mining big meteorological data. Proceedings of the 13th International Conference on Intelligent Computing. Liverpool, UK. 2017. 57–66.
|
| [4] |
王金策, 邓越萍, 史明, 等. 多时间尺度时间序列趋势预测. 计算机应用, 2019, 39(4): 1046-1052. DOI:10.11772/j.issn.1001-9081.2018091882 |
| [5] |
郁伟生, 邓伟, 张瑶, 等. 基于时间序列的音乐流行趋势预测研究. 计算机工程与科学, 2018, 40(9): 1703-1709. DOI:10.3969/j.issn.1007-130X.2018.09.024 |
| [6] |
郑荣, 颜七笙. 基于ARIMA与SVM的国际铀资源价格预测. 计算机工程与应用, 2016, 52(1): 146-150. DOI:10.3778/j.issn.1002-8331.1401-0234 |
| [7] |
董新科, 张晖. 基于校园一卡通消费数据的几种聚类算法的分析比较. 计算机系统应用, 2014, 23(1): 158-161, 183. DOI:10.3969/j.issn.1003-3254.2014.01.031 |
| [8] |
张栗粽, 王谨平, 刘贵松, 等. 面向金融数据的神经网络时间序列预测模型. 计算机应用研究, 2018, 35(9): 2632-2637. DOI:10.3969/j.issn.1001-3695.2018.09.017 |
| [9] |
成云, 成孝刚, 谈苗苗, 等. 基于ARIMA和小波神经网络组合模型的交通流预测. 计算机技术与发展, 2017, 27(1): 169-172. |
| [10] |
张颖, 陈卓. 改进ARIMA模型在医药需求预测中的研究. 计算机工程与设计, 2018, 39(1): 183-188, 295. |
| [11] |
汪鹏, 彭颖, 杨小兵. ARIMA模型与Holt-Winters指数平滑模型在武汉市流感样病例预测中的应用. 现代预防医学, 2018, 45(3): 385-389. |
| [12] |
唐宏, 唐诗华, 陈雨田, 等. Holt-Winters与ARIMA模型在电离层总电子含量预报中的比较. 桂林理工大学学报, 2019, 39(4): 905-911. DOI:10.3969/j.issn.1674-9057.2019.04.015 |
| [13] |
郁抒思, 周水庚, 关佶红. 软件工程数据挖掘研究进展. 计算机科学与探索, 2012, 6(1): 1-31. DOI:10.3778/j.issn.1673-9418.2012.01.001 |
| [14] |
焦飞, 黄天文. 时间幂函数与LSF在气温预测中的应用研究. 肇庆学院学报, 2017, 38(5): 1-4, 8. DOI:10.3969/j.issn.1009-8445.2017.05.001 |
| [15] |
郑海鹏. 基于SPSS多元线性回归的高校学生就业薪资期望分析. 齐齐哈尔大学学报(自然科学版), 2019, 35(6): 77-81. DOI:10.3969/j.issn.1007-984X.2019.06.020 |
| [16] |
张郑贤, 刘艺, 张锋贤. 基于时间序列模型的济南趵突泉地下水位预测. 中国水利水电科学研究院学报, 2019, 17(1): 51-59. |
| [17] |
王宇飞, 杜天苍. 基于Holt-Winters的时间序列预测在大数据监控系统中的分析与应用. 计算机与现代化, 2019(11): 29-33. DOI:10.3969/j.issn.1006-2475.2019.11.006 |
| [18] |
宋雨, 焦谱, 李刚. 大数据预处理中属性约简的特性保持分析. 计算机测量与控制, 2015, 23(12): 4191-4194. |
| [19] |
Arevalo F, Cid A, Moya J. AIC and BIC for cosmological interacting scenarios. The European Physical Journal C, 2017, 77: 565. DOI:10.1140/epjc/s10052-017-5128-7 |
| [20] |
Liang GP, Fu WL, Wang KF. Analysis of t-test misuses and SPSS operations in medical research papers
. Burns & Trauma, 2019, 7: 31. DOI:10.1186/s41038-019-0170-3 |
| [21] |
Sun SH, Zhou MH. Analysis of farmers’ land transfer willingness and satisfaction based on SPSS analysis of computer software. Cluster Computing, 2019, 22(4): 9123-9131. DOI:10.1007/s10586-018-2087-1 |
| [22] |
Chortatos A, Terragni L, Henjum S, et al. Consumption habits of school canteen and non-canteen users among Norwegian young adolescents: A mixed method analysis. BMC Pediatrics, 2018, 18(1): 328. DOI:10.1186/s12887-018-1299-0 |
| [23] |
游香薷, 王业, 杨抒, 等. 学生消费行为的聚类分析优化研究和应用. 计算机系统应用, 2017, 26(6): 232-237. DOI:10.15888/j.cnki.csa.005798 |
 2021, Vol. 30
2021, Vol. 30



