高校学生成绩一直是直接评价学生学业水平的重要指标, 也是间接评价高校教师教学效果及高校管理水平的指标之一^[1]. 随着高校学生成绩信息量的不断增加, 对学生成绩进行简单的统计、对比等信息处理方式难以满足学生和教育工作者的实际需求, 学生成绩预警研究已成为当今高校信息管理领域研究的热点^[2-5].

成绩预警是指通过对学生课程成绩进行分析, 挖掘各门课之间的联系, 基于已有的成绩数据, 对学生未来的成绩走向进行预警. 挖掘课程之间的相互联系, 构建完善的预警规则库是学生成绩预警研究中的关键点^[6-9]. 高校课程之间具有很强的关联性^[10], 这种关联性体现在专业知识体系构建以及知识传授的前后次序. 挖掘深层次的课程关联关系, 可以为学生成绩的预警分析提供决策支持, 对高校提高教学管理水平具有重要应用价值.

关联规则挖掘^[11]是数据挖掘中一种重要的数据分析方法, 这其中经典的Apriori算法^[12]可有效地从某一任务的事务集中挖掘出客户感兴趣且富有价值的隐藏规则. 近年来, 将Apriori算法应用在高校成绩预警分析中成为一个研究热点, 何楚等^[13]采用Apriori算法和FP-growth算法挖掘学生成绩的频繁规则并结合基于图论的谱聚类算法对规则中涉及的公共课与专业课进行分类, 提出基于课程关联分类模型的学生成绩预测, 研究方法新颖, 但仅采用支持度与置信度进行规则挖掘, 没有剔除某些有较强干扰性的规则; 郭鹏等^[14]在对学生成绩进行聚类离散化后, 再引入兴趣度挖掘课程间的关联规则, 其侧重点在于不同等级成绩之间的课程规则挖掘, 而非针对不及格课程之间的规则挖掘; 王华等^[15]为减少Apriori算法的I/O负载, 利用交集操作记录频繁项集从而降低时间代价, 不足点在于受限Matlab平台; 刘华婷等^[16]针对Apriori算法的效率问题提出采用线性表进行数据存储, 利用Apriori算法中的超集定理判断非频繁项集, 从而在扫描速度上进行优化, 加快算法的时间效率, 遗憾的是该研究仅在单一且规模较小的数据集上进行了效率测试; 袁路妍等^[17]通过减少Apriori算法中挖掘频繁项集的比较次数, 以提升算法的效率, 该法所挖掘出的规则在度量上仍只采用了支持度与置信度; 赵峰等^[18]借鉴分治算法的思想, 提出将事务集中的课程进行预分类, 再得到各自类别的频繁项集进行规则挖掘, 虽避免了扫描整个事务集, 但仍无法保证规则的有效性.

综上, Apriori算法在高校成绩预警应用中的基本思想: 一是对课程或学生成绩本身进行类别处理, 再通过引入一种新的参数对挖掘出的规则进行有效性度量; 二是针对Apriori算法自身存在的运行效率缺陷提出改进, 加强Apriori算法的适用性. 对此, 本研究在传统的Apriori算法之上提出利用提升度筛选出彼此关联程度较高的课程规则, 再引入兴趣度针对预警规则库所需求的课程规则进行筛选, 最终得到兴趣度较高的关联规则构建课程预警规则库, 相比较传统Apriori算法, 本研究提出的算法能大大降低了冗余规则数量, 缩短算法运行时间, 提高规则挖掘的效率.

1 高校课程预警规则分析方法 1.1 相关定义

定义1. 项.

定义集合 $I = \{ {i_1},{i_2},\cdots,{i_m}\}$ 表示由 ${{m}}$ 个元素组成的一个有限集合. 设相关问题数据集D是本问题的事务集合: $D = \{ {T_1},{T_2},\cdots,{T_{{n}}}\}$ , 它是由个 $n$ 事务T组成. 现规定D集中某一元素 ${T_i}$ 由一或多个I集中的元素 ${i_j}$ 构成, 即 $T \subseteq I$ 且 $T \ne \emptyset ,i = 1,2,\cdots,n;j = 1,2,\cdots,m$ .

定义2. 候选项集.

由一或多个项组成的集合 $\{ {i_1},{i_2},\cdots,{i_k}\}$ 称为候选项集, 包含 $k$ 个项的候选项集称为 $k$ 候选项集, 如A={面向对象程序设计(及格)、软件工程(及格)}是一个2—候选项集, 且 $A \subseteq T$ .

定义3. 频繁项集L_k.

若该候选项集A的绝对支持度support(A)满足算法中预设定的最小支持度阈值sup_min, 也即 $support\left( A \right) \ge $ $ {sup _{\min }}$ 时, 则称该项集A为频繁项集, 包若A中含个 $k$ 项则称为频繁 $k$ 项集 ${L_k}$ ; 当时 $k \ge 2$ , 可挖掘 ${L_k}$ 中不同项之间的关联规则.

定义4. 关联规则.

本算法中所有的关联规则都是由频繁 $k$ -项集 ${L_k}$ 得到的, 例如频繁2—项集={面向对象程序设计(及格)、软件工程(及格)}同时又满足Apriori算法的最小置信度阈值 $con{f_{\min }}$ , 则A可产生一条由蕴含式表示的规则: {面向对象程序设计(及格) $ \Rightarrow $ 软件工程(及格)}, 其中“面向对象程序设计(及格)”为规则的前件, “软件工程(及格)”为规则的后件. 规则的支持度计算公式如下:

$support\left( {X \Rightarrow Y} \right) = count(X \cup Y)/count(D) = p(X \cup Y)$

(1)

其中, $count(X \cup Y)$ 表示X与Y的并集在事务集D中的计数, $count(D)$ 表示事务集D中事务数. 规则的置信度计算公式如下:

$confidence\left( {X \Rightarrow Y} \right) = p(X \cup Y)/p(X) = p(Y|X)$

(2)

支持度与置信度是对规则筛选最重要的两种度量, 规则的支持度反映所发现规则的价值性及在事务集中出现的频率, 置信度则反映了规则的确定性^[19].

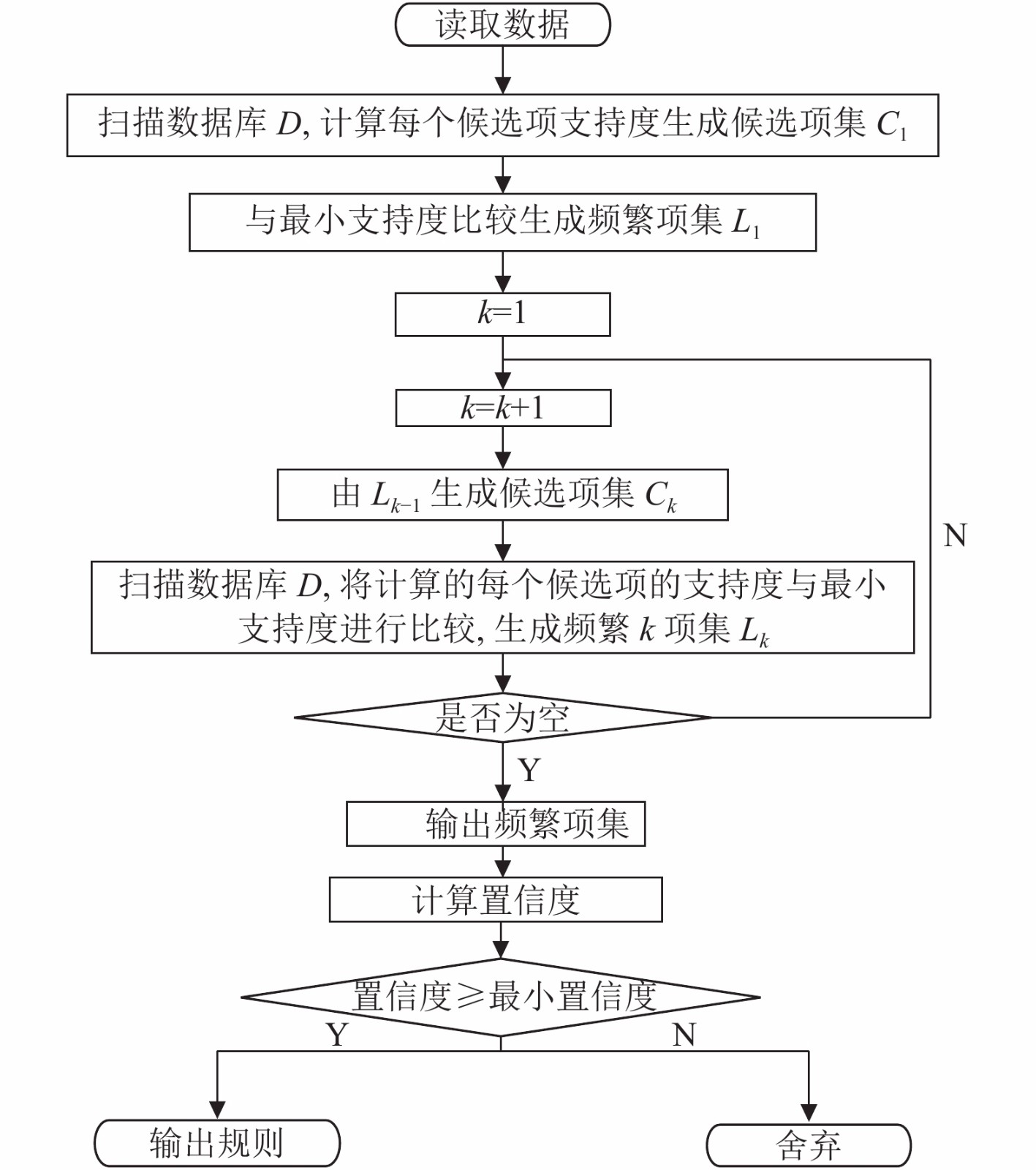
1.2 传统的Apriori算法课程预警规则挖掘算法

传统的Apriori算法课程预警关联规则挖掘利用逐层迭代的搜索方法, 即由生成的频繁 $k$ —项集确定频繁 $(k + 1)$ 项集的思想. 传统的Apriori算法课程预警规则挖掘的算法流程如图1, 其主要步骤为两个阶段.

第1阶段, 算法执行后扫描事务集D, 记录每个项的频数, 并根据最小支持度阈值筛选出符合要求的候选频繁项集, 记为 ${L_1}$ ; 然后利用 ${L_1}$ 找出满足最小支持度阈值频繁2-项集, 记为 $L{}_{_2}$ , 如此反复迭代, 直到没有满足最小支持度阈值的频繁 $k$ -项集.

第2阶段, 再次扫描所有的频繁 $k$ -项集, $k = 1,2,\cdots$ ; 利用第1阶段中得到的支持度数据计算每一个频繁 $k$ -项集的置信度, 将满足最小置信度阈值的频繁 $k$ -项集挖掘筛选出符合课程预警的规则, 进行构建规则库.

1.3 改进的Apriori课程预警关联规则算法 1.3.1 增强冗余规则筛选机制

传统的关联规则挖掘算法使用支持度-置信度框架作为筛选依据, 但支持度-置信度框架存在一定的缺陷. 其中支持度的缺点是显而易见的, 在事务集中会有许多潜在的有意义的模式由于其频繁项集L_k支持度小而被忽略或者产生一些冗余的规则; 而置信度的缺陷却比较特殊, 它主要在于忽视了规则后件的项集在事务集中的支持度. 因此, 通过传统的Apriori算法生成的预警规则库会出现很多无用、冗余的关联规则, 对成绩预警分析产生干扰, 降低预测的准确性, 因而需要对预警关联规则作进一步地度量分析, 从而筛选出合适的预警规则. 对此, 本研究在支持度-置信度框架基础上引入提升度Lift^[20]、兴趣度Interest^[21]对挖掘关联规则算法进行改进.

提升度方面, 某一频繁k项集生成的某规则 $\{ X \Rightarrow $ $ Y\} $ 的提升度被定义为:

$\begin{split} Lift\left( {X \Rightarrow Y} \right) &= p(X \cup Y)/p(X)p(Y) \\ & = confidence\left( {X \Rightarrow Y} \right)/support\left( Y \right) \end{split}$

(3)

当该条规则的Lift值小于1时表示X和Y是负相关的, 一个出现可能导致另一个不出现; 当值Lift近似等于1时表示X和Y是独立的, 彼此之间无相关性; 当Lift值大于1时表示表示X和Y是正相关的, 其中一个的出现会蕴涵另一个的出现. 提升度越高则表示由规则前件主导与规则后件共同出现的程度越高, 反之提升度越小时则二者互斥的程度越高.

兴趣度方面, 本研究引入基于差异思想的兴趣度^[22,23]. 某一频繁k项集生成的某规则 $\{ X \Rightarrow Y\} $ 的兴趣度的定义如下: 由该条规则 $\{ X \Rightarrow Y\} $ 的置信度与规则后件的支持度之间的差值作为分子; 分母则取该条规则 $\{ X \Rightarrow Y\} $ 的置信度与规则后件支持度的最大值, 也即引入了一个标准化因子, 整体上使得该条规则的兴趣度绝对值小于1.

区别于提升度筛选前后件关联程度较高的规则, 兴趣度可对某频繁k-项集产生的正反面规则筛选得到用户更感兴趣的规则. 如对于某一频繁2-项集A={面向对象程序设计(及格)、软件工程(及格)}, 由于前后件的不同可产生两条规则: {面向对象程序设计(及格) $\Rightarrow $ 软件工程(及格)}、{软件工程(及格) $\Rightarrow $ 面向对象程序设计(及格)}, 根据前文兴趣度的定义, 二者的兴趣度值显然不一; 那么, 通过兴趣度阈值就可筛选出以“面向对象程序设计(及格)”为前件的预警规则. 引入兴趣度的目的在于可选择某些不及格的重点课程作为前件, 挖掘出相关预警规则, 从而摒弃某些兴趣度不高的规则.

1.3.2 计算候选集频数优化策略

在Apriori算法中, 由频繁项集 ${L_{k - 1}}$ 自连接得到候选集 ${C_k}$ 的过程中, 存在两大缺陷: 一是由于 ${L_{k - 1}}$ 中存在很多不必作自连接的项集, 导致产生冗余 ${C_k}$ ; 二是需要多次扫描数据库确定候选项集支持度^[24]. 针对上述问题, 提出一种计算候选集频数优化策略.

首先通过矩阵运算的方法获得频繁一项集 ${L_1}$ , 并对 ${L_1}$ 进行预剪枝得到 ${L_1}$ , 然后利用Apriori算法的自连接性质对 ${L_1}$ , 进行操作生成候选二项集 ${C_2}$ . 在计算候选二项集 ${C_2}$ 的支持度计数之前, 首先要根据 ${L_1}$ 明确 ${I_x}$ 和 ${I_y}$ 中的最小项, 接下来在搜索频繁项集时候只需要扫描特定分支即含有最小项事务结点链而不是整个数据库, 并结合该节点处标记 $fla{g_i} = (x,y)$ 中 $y$ 的数值, 即可得到 ${C_2}$ 的计数, 最后对 ${C_2}$ 进行剪枝得到频繁二项集 ${L_2}$ , 对获得的频繁二项集 ${L_2}$ 作同样的操作就可以快速计算出 ${C_3}$ 支持度计数, 节省了空间和时间资源.

1.3.3 基于矩阵的存储方式改进

将事务数据库D转换为矩阵, 每一事务以矩阵的行来表示行纬度, 事务中的项用列表示列维度, 当要对数据进行挖掘时就可以直接调用转换为矩阵中的信息, 在行列指定的位置处若存在数据则为1, 否则记为0, 删除事务长度小于最小置信度的行与列, 免去了对D再次扫描的过程, 节省了I/O的开销与时间.

改进Apriori的课程预警关联规则算法伪代码如算法1.

算法1. 改进的课程预警关联规则算法

输入: 事务集D, 最小支持度, $\scriptstyle{sup _{\min }}$ 最小置信度 $\scriptstyle con{f_{\min }}$ , 最小提升度 $\scriptstyle Lif{t_{\min }}$ , 最小兴趣度 $\scriptstyle Interes{t_{\min }}$

输出: 预警规则列表 $\scriptstyle R$

1) 扫描事务集D, 生成候选项集矩阵 $\scriptstyle{C_1}$ 并计算其support;

2) 将候选项集 $\scriptstyle{C_1}$ 的support与 $\scriptstyle{sup _{\min }}$ 进行比较, 生成频繁项集 $\scriptstyle{L_1}$ ;

3) for(k=2; L_k−1≠ $ \scriptstyle\emptyset $ ; k++):

4) 剪枝并生成新的候选项集 $\scriptstyle{C_k}$ ;

5) 再次扫描事务集D, 计算 $\scriptstyle{C_k}$ 的support;

6) 将C_k的support与 $\scriptstyle{sup _{\min }}$ 比较, 生成频繁项L_k;

7) 输出频繁项集列表L;

8) for(k=2; k<=len(L); k++): //遍历频繁项集列表L

9) 提取每一个 $\scriptstyle{L_k}$ 并计算置信度; 并与 $\scriptstyle con{f_{\min }}$ 比较后筛选;

10) 计算每一个 $\scriptstyle{L_k}$ 的提升度Lift, 与 $\scriptstyle Lif{t_{\min }}$ 比较后筛选;

11) 计算每一个 $\scriptstyle{L_k}$ 的兴趣度Interest, 与 $\scriptstyle Interes{t_{\min }}$ 比较后筛选;

12) 由筛选后的 $\scriptstyle{L_k}$ 生成预警规则 $\scriptstyle{R_k}$ ;

13) 输出预警规则列表R.

2 实验结果与分析 2.1 实验环境与数据来源

本研究的实验硬件环境为Intel Core i7处理器、16 GB内存, 1 TB硬盘; 操作系统选用Mac OS系统; 选用Python 3.7并在Jupyter notebook开发环境上对实验进行编程实现.

实验数据来源于新疆师范大学计算机科学技术学院毕业学生的19门基础课与核心专业课的成绩, 共3000条记录, 部分原始数据如表1 所示.

2.2 数据的清洗

由于部分原始数据中出现了不同专业间相关开设的课程名称前后不一致的现象, 必须对其进行一致化处理: 如高等数学(1)与高等数学(I)统称为高等数学一、面向对象程序设计(Java)与面向对象程序设计统称为面向对象程序设计, 计算机网络与计算机网络技术统称为计算机网络.

本研究主要挖掘是专业课程的相关关系, 特别是不同学期开始的专业基础课与核心专业课程之间的联系, 可将原始数据中与专业无关的公共类、博雅类课程进行剔除, 仅选取如高等数学、数据结构、Web技术与应用等19门学科课程作为研究对象.

对于某些学生成绩大面积缺失的, 则采取舍弃该样本, 若学生出现补考成绩的需进行成绩的一致性处理. 对于某些学生出现某科科目成绩出现空值的情形, 则采用该学科的均值成绩填充.

2.3 数据的离散化

课程成绩本身也就是一种离散化数据, 若将课程成绩的分值直接作为Apriori算法的事务集进行输入, 其挖掘出来的规则适用性较低且模型效率低. 由于考试方式、考试难度、评卷的标准存在差异性, 课程成绩的分布有可能相对集中在某一个小区间内, 而非在各个分值区间中呈现出相似的密度. 本研究针对事务集中550条记录, 决定采用基于单值的划分方法, 设定课程成绩区间, 划分课程成绩等级, 以便于更好的挖掘课程之间的联系. 所得的成绩等级划分表如表2.

2.4 预警规则挖掘对比实验及分析

为验证改进算法的效率, 分别采用传统Apriori算法, MIFP-Apriori^[24], RCM-Apriori^[25], 与本文提出的算法进行预警规则的挖掘, 对效率进行对比. 在事务集为3000的数据集上, 选用最小值支持度阈值0.1, 最小置信度阈值0.4的进提升度阈值1.4、兴趣度阈值0.1执行算法实验, 4种算法所挖掘出的无用冗余规则条数和运行时间见表3, 由表3可以看出本文提出的改进的Apriori算法可以大大降低冗余规则条数, 算法运行时间也得到缩短, 提高了预警规则的挖掘效率.

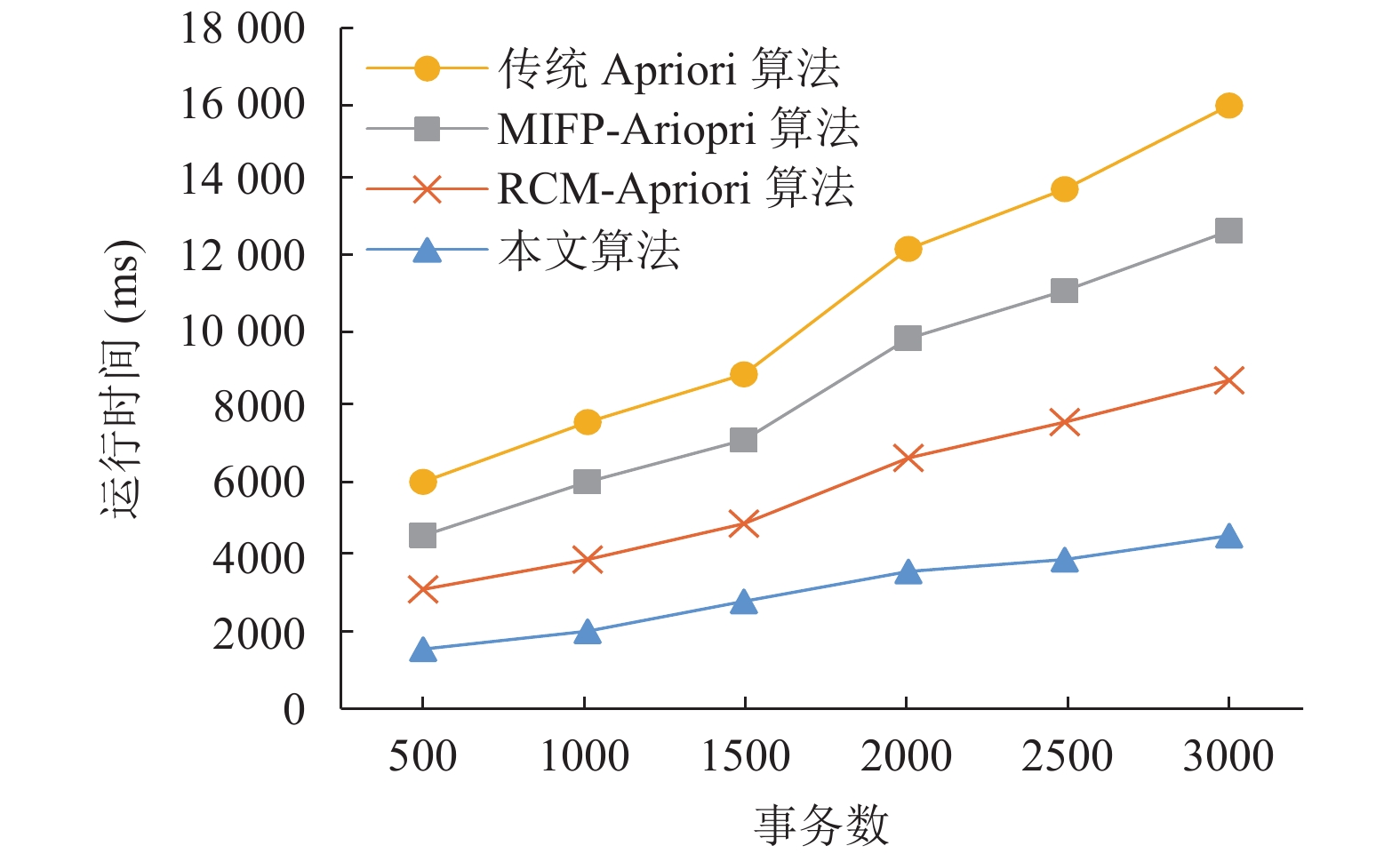
为进一步测试在不同事务集大小下的各算法执行效率, 将事务集按照500~3000进行递增, 考察不同数据规模下算法的运行时间, 实验结果如图2所示.

由图2可以看出, 当数据规模较小时, 4种算法的执行时间相差不大. 当数据规模逐渐增加时, 传统的Apriori算法斜率增加比较明显, 执行时间最长, 本文提出的算法在候选项集生成, 冗余规则筛选, 存储方式等方面进行了优化, 曲线斜率比其他3种算法小, 运行时间最短, 并且性能稳定.

本文提出的改进的Apriori算法在剔除掉无关的1324条冗余规则后, 共挖掘到有效规则430条. 部分规则如表4所示.

表4中第2条规则{页设计基础(不及格) $\Rightarrow $ ('Web技术与应用(不及格)}揭示了Web技术与应用的与前导课网页设计基础存在紧密联系, 若学生出现《网页设计基础》课程不及格时, 那么很有可能在学习《Web技术与应用》课程时成绩同样会不及格. 再如第4条规则{离散数学(不及格) $\Rightarrow $ (数据结构(不及格))}, 离散数学作为数据结构的重要基础之一, 一旦学生出现离散数学不及格的情况, 则有大概率发生数据结构同样不及格的情况.

3 结束语

高校课程预警规则库可以为学生成绩预警提供决策支持, 本文对学生成绩进行预处理后, 采用Apriori算法, 重点挖掘不及格课程之间的关联关系, 构建基础预警规则库, 挖掘强关联关系的课程, 扩充基础预警规则库, 采用多种方式对冗余规则进行过滤, 确保预警规则库的有效性. 挖掘出的课程预警规则, 可为课程成绩的预测, 高校教学方案的设计提供数据支撑, 有助于提升高校的教学质量.