随着互联网规模的不断扩大, 各种接入设备和相关的数据类型也日益繁杂, 传统IP网络的管理方法已经无法满足大量新型应用服务对设备快速部署与技术实时更新的需求, 同时网络管理者在面对网络资源的合理化配置等任务时也遇到了较大的困难, 这些问题都极大地增加了新技术的应用成本. 软件定义网络SDN(Software Defined Network)技术改变了传统IP网络的四层协议体系, 将数据传输与网络控制两个主要环节相互解耦[1], 从而使得用户可以通过控制层提供的统一且便捷的管理工具, 以全局化的视角实现对分布式网络的集中调控, 并依据自身需求灵活的配置各类网络资源, 显著地提高了大规模网络的运维管理水平[2]. 作为全类型网络管理的关键依据, 网络流量的特征及变化规律同样也成为了SDN技术研究的热点, 因此针对IP网络流量预测技术进行改进, 设计一款符合SDN网络流量特征的、精确度高的网络流量预测模型, 以帮助网络应用开发人员更准确地分析SDN网络性能波动状态和优化网络资源配置, 具有重要的理论意义和应用价值.
目前针对网络流量进行预测的方法很多, 基本可分为两个主要类型, 第1类是以时间序列法为核心, 即根据网络流量在历史时间序列中的变化规律预测下一个有限时间间隔内的变化趋势, 如王逸兮等人提出采用同点时间序列构建检测模型, 提高了网络性能异常的检出率[3], Auld等人则设计了一套网络流量信息的规范化预处理算法, 有效地控制了预测模型的计算规模[4]; 叶德忠等人提出构建马尔可夫时变模型来完成针对网络流量信息挖掘工作, 降低了预测误差[5]等. 这一类模型对于传统IP网络流量的监测效果较好, 但对于具备长相关性特征的SDN网络数据流的预测精度则不太理想[6]. 第2类方法是以神经网络等智能算法为核心构建网络流量预测模型, 如李晓方等人提出对源-目的流(OD流)数据进行降维, 并以Elman神经网络对低维度样本进行训练, 从而发挥了SDN网络可实现精确测量数据流的优势[7]; NAREJOS等人提出通过构建深层神经网络的方式提高对样本群的训练质量, 提高了预测精度, 但算法的空间复杂度也大幅上升[8]. 神经网络存在一些固有的缺陷, 如对训练样本要求过高, 对待有限的样本群时, 缺乏足够的泛化能力; 网络结构无法动态调整, 训练时间过长; 神经元规模可控性差, 极易陷入“维数灾”难题等[9].
支持向量机(SVM)作为一种基于统计学习理论的人工智能算法, 具有良好的泛化能力与非线性处理能力[10], 近年来在样本群分型与模式识别领域得到广泛的应用. 如王鸣提出采用小波技术结合SVM构建流量预测模型, 良好地控制了计算规模, 提升了预测模型的执行效率[11]. 但根据目前的研究成果来看, 与传统IP网络相比, SDN网络流量的特征呈现出更为突出的混沌性、时变性和自相似性, 这使得SVM技术必须在非线性混沌理论的辅助下, 方可通过数学建模来描述复杂的网络流量变化规律. 因此本文提出采用混沌理论中的多维相空间重构技术对SDN网络流量数据进行预处理, 构建相空间中的样本矩阵, 随后采用改进后的粒子群算法(PSO)对最小二乘支持向量机(LSSVM)中的关键参数进行优化, 有效的提高了LSSVM的运算效率, 并构建针对网络流量变化趋势的预测模型, 对SDN网络流量样本群进行训练. 通过仿真实验证明, 该模型与其他同类模型相比, 在合理控制计算复杂度的条件下, 表现出了更高的预测精度和误差控制能力.
2 基于混沌理论的相空间重构相空间重构理论由Takens等人提出, 该理论将多维状态空间中任一点的变化规律视为与之产生关联的其它点变化的综合影响, 因此可构建相对时间序列. 该序列中的任一点在起始时间点上的值设为基值, 而在空间中其他延迟坐标点上的值则作为新维来处理. 随着起始时间点的推移, 不断构建出新的子序列, 就可通过监测空间中各个时间点变化规律的方式, 完整的构建出系统的动态模型[12].
假设混沌时间序列为
| $ \left\{ {\begin{split} &X = \left\{ {{X_i}|{X_i} = {{\left[ {{x_i},{x_{i + \tau }}, \cdots ,{x_{i + (m - 1)\tau }}} \right]}^{\rm{T}}},i = 1,2, \cdots ,M} \right\}\\ &M = N - (m - 1)\tau \end{split}} \right. $ | (1) |
设系统动力学维数为d, Takens同样证明了若嵌入维m能够满足
| $C\left( {m,N,r,\tau } \right) = \frac{2}{{M(M - 1)}}\sum\limits_{1 \le i < j \le M} {\theta \left( {r - {d_{ij}}} \right),r > 0} $ | (2) |
式中,
| $\left\{ {\begin{split} {x^1} =& \left\{ {{x_i}|i = 1,\tau + 1, \cdots ,N - \tau + 1} \right\} \\ {x^2} =& \left\{ {{x_i}|i = 2,\tau + 2, \cdots ,N - \tau + 2} \right\} \\ &{ \vdots } \\ {x^t} = &\left\{ {{x_i}|i = \tau ,2\tau , \cdots ,N} \right\} \end{split}} \right.$ | (3) |
由此可将检验统计量表达为:
| ${S_1}\left( {m,N,r,\tau } \right) = C\left( {m,N,r,\tau } \right) - {C^m}\left( {1,N,r,\tau } \right)$ | (4) |
对上式进行分块平均, 可得到:
| ${S_2}\left( {m,N,r,\tau } \right) = \frac{1}{t}\sum\limits_{s = 1}^t {\left[ {{C_s}\left( {m,{N / \tau },r,\tau } \right) - C_s^m\left( {1,{N / \tau },r,\tau } \right)} \right]} $ | (5) |
当
| ${S_2}\left( {m,r,\tau } \right) = \frac{1}{t}\sum\limits_{s = 1}^t {\left[ {{C_s}\left( {m,r,\tau } \right) - C_s^m\left( {1,r,\tau } \right)} \right]} $ | (6) |
当处于时间序列无限长且各元素之间不相关的理想条件下时, 若m和τ为定值, 则对于
| $\begin{split} {\tau _d} &= \min \left( {\Delta {S_2}\left( {m,\tau } \right)} \right) \\ &\begin{array}{*{20}{c}} \!\!={ \min \left( {\max \left( {{S_2}\left( {m,{r_j},\tau } \right)} \right){\rm{ - min}}\left( {{S_2}\left( {m,{r_j},\tau } \right)} \right)} \right)} \end{array} \\ \end{split} $ | (7) |
确定了最佳重构时延τ后, 即可逆向推导得到嵌入维m的最佳值, 并完成时间序列在多维相空间中的重构.
3 基于改进PSO算法的LSSVM的优化 3.1 最小二乘支持向量机LSSVM支持向量机(SVM)具有良好的泛化能力, 但对于一个新的样本群进行训练时, 其计算复杂度高成为了一个很难克服的问题, 这就导致了当面对以时间序列构建的大规模SDN网络流量样本群时, SVM的执行效率会大幅降低, 从而严重地影响了预测模型的实时性能[14]. Este A等人提出采用最小二乘法对SVM进行改进, 引入误差平方和替代SVM中的损失函数, 通过非线性映射函数φ(x)将低维空间中的平面分类问题转化为高维空间的线性方程组求解问题, 从而有效地降低了原算法的复杂度[15].
对于一个记录了输入量
| $y\left( x \right) = {w^{\rm{T}}}\varphi \left( x \right) + b$ | (8) |
式中, w表示高维特征空间采用的权值向量, b为预设的偏置常数.
参照支持向量机理论, 可采用式(9)中列出的回归模型求解上述回归函数, 有:
| $\left\{ {\begin{split} & \mathrm{min} J\left(w,e\right)=\frac{1}{2}{w}^{\rm{T}}w+\frac{1}{2}\gamma {\displaystyle \sum _{i=1}^{n}{e}_{i}^{2}} \\ & {\rm {s.t.}}\begin{array}{cc}\;\; {y}_{i}={w}^{\rm {T}}\phi \left({x}_{i}\right)+b+{e}_{i},\; i=1,2,\cdots ,n\end{array} \end{split}} \right.$ | (9) |
该模型使用的正则化方法非常有助于提高模型的泛化能力, γ为正则化参数,
| $L\left( {w,b,e,\alpha } \right) = J\left( {w,e} \right) - \sum\limits_{i = 1}^n {{\alpha _i}\left( {{w^{\rm{T}}}\varphi \left( x \right) - b + {e_i} - {y_i}} \right)} $ | (10) |
式中,
| $K\left( {{x_i},{x_j}} \right) = {\rm{exp}}\left( { - \frac{{{{\left\| {\left( {{x_i} - {x_j}} \right)} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$ | (11) |
对式(10)中的
| $\hat y\left( x \right) = \sum\limits_{i = 1}^N {{\alpha _i}} K\left( {{x_i},{x_j}} \right) + b$ | (12) |
LSSVM模型的拟合能力主要依赖正则化参数γ和核函数宽度值σ的选取质量, 其中γ影响了模型的拟合精度与泛化能力, σ则直接决定了模型的计算量与执行效率[16,17]. 目前通常采用的选取方法有网络搜索算法和遗传算法等, 前者的计算规模庞大, 算法实时性差, 后者则容易陷入局部极值陷阱问题, 本文提出采用改进粒子群算法实现对LSSVM模型参数(γ, σ)的组合优化, 取得了较好的参数寻优质量.
粒子群算法(PSO)针对群体内的每个粒子的位置与速度进行跟踪和调整, 从而实现对整个群体的优化效果[18]. 假设采用d维向量对以上两种状态分别进行描述, 则有
| $\left\{ {\begin{split} & v_{id}^{k + 1} = \omega {v_{id}} + {c_1}{r_1}\left( {{p_{id}} - {\textit{z}}_{id}^k} \right) + {c_2}{r_2}\left( {{p_{sd}} - {\textit{z}}_{id}^k} \right) \\ & {\textit{z}}_{id}^{k + 1} = {\textit{z}}_{id}^k + v_{id}^{k + 1} \end{split}} \right.$ | (13) |
式中, ω为惯性权重,
| $\omega = \left\{ {\begin{array}{*{20}{l}} {{\omega _{\min }} - \dfrac{{\left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {f - {f_{\min }}} \right)}}{{{f_{\rm {avg}}} - {f_{\min }}}},f < {f_{\rm {avg}}}} \\ {{\omega _{\max }},\;}{\rm{otherwise}} \end{array}} \right.$ | (14) |
式中, f为当前粒子个体的适应度,
| $\left\{ {\begin{array}{*{20}{l}} {{c_1} = - 2 \times \dfrac{k}{{{K_{\max }}}} + 2.5} \\ {{c_2} = 2 \times \dfrac{k}{{{K_{\max }}}} + 0.5} \end{array}} \right.$ | (15) |
式中,
对参数寻优效果进行分析, 首先, 根据式(13)可以看出,
惯性权重参数ω的作用是帮助粒子个体构建全局搜索能力, 对ω进行合理的调节, 将有效的影响算法在全局搜索和局部搜索两方面侧重倾向[20], 若式(13)中缺少了第一项
1)
2)
3)
以上3种情况均会对算法造成极大的干扰, 粒子个体将会出现加速度恒定和移动方向固定等问题, 因此当失去了加速参数
在引入了改进PSO算法之后, 采用实数编码将(γ, σ)组成一个粒子, 随后结合式(9)至式(12)的推导过程, 构建出优化后的预测模型, 如式(16)所示:
| $\left\{ { \begin{split} &\mathrm{min}J=\mathrm{min}f({{\textit{z}}}_{i})=\frac{1}{L}{\displaystyle \sum _{i=1}^{n}\left({y}_{i}-{\hat{y}}_{i}\right)} \\ & {\rm {s.t.}}\begin{array}{cc}& \gamma \in \left[{\gamma }_{\mathrm{min}}, {\gamma }_{\mathrm{max}}\right], \sigma \in \left[{\sigma }_{\mathrm{min}}, {\sigma }_{\mathrm{max}}\right]\end{array} \end{split}} \right.$ | (16) |
适应度函数取预测值与真实值之间的误差总和, 即:
| $f( \cdot ) = \sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} $ | (17) |
其中,
对算法各主要环节描述如下:
Step 1. 采集SDN网络流量历史数据, 构建时间序列的样本群, 并采用C-C算法获取最佳的嵌入维和重构时延, 在此基础上完成对原样本群的相空间重构, 得到规范化的数据序列;
Step 2. 对PSO算法执行初始化操作, 确定样本群规模、迭代轮次数、粒子初始状态(位置
Step 3. 将(γ, σ)参数组成粒子个体, 并采用随机取值法构建初代粒子群体;
Step 4. 根据式(17)计算群体中粒子个体的适应度, 调整本轮次中ω、
Step 5. 依据适应度值判断参数寻优目标是否完成, 若达要求则将本轮次寻得的最优粒子取出, 按照实数编码规则解析出对应的(γ, σ)作为LSSVM的优化参数, 否则返回Step 4, 进入下一轮次的迭代训练;
Step 6. 利用求得的参数和重构的训练样本对LSSVM进行求解, 构建网络流量预测模型, 并使用验证样本群进行对照分析, 输出最终的预测结果.
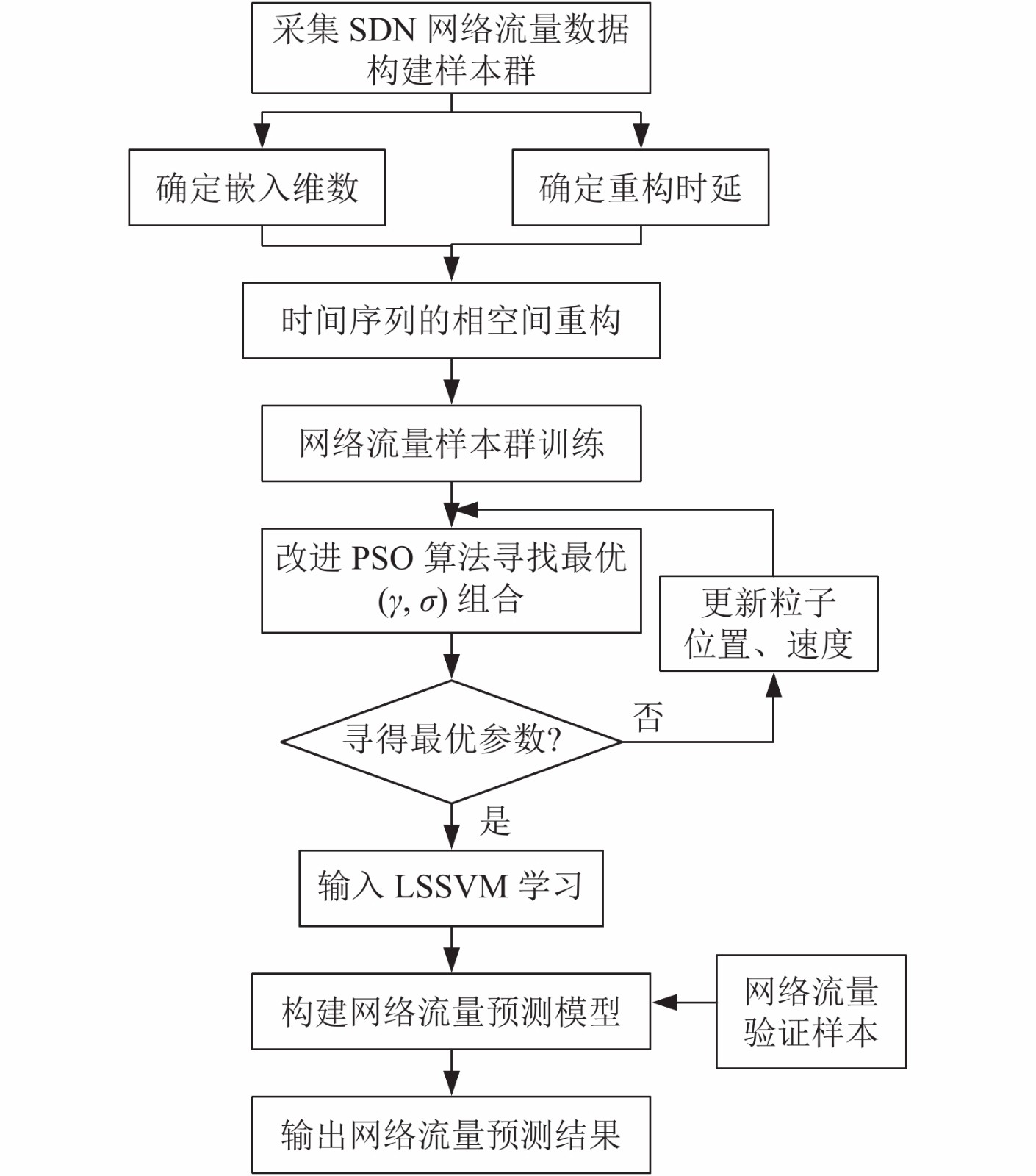
|
图 1 预测算法执行流程 |
4.2 实验设计与结果分析
在数据样本的选择上, 采用在美国Abilene网络上采集到的真实数据展开仿真实验分析. 该数据集汇聚了一个包括30条链路在内的SDN-IP混合网络中的流量信息, 其中SDN-OD流46条, IP-OD流为108条, 数据采样周期为5 min, 选择其中1000条流量数据, 前800条数据作为训练样本群, 后200条作为验证样本群, 其中部分样本信息如图2所示.
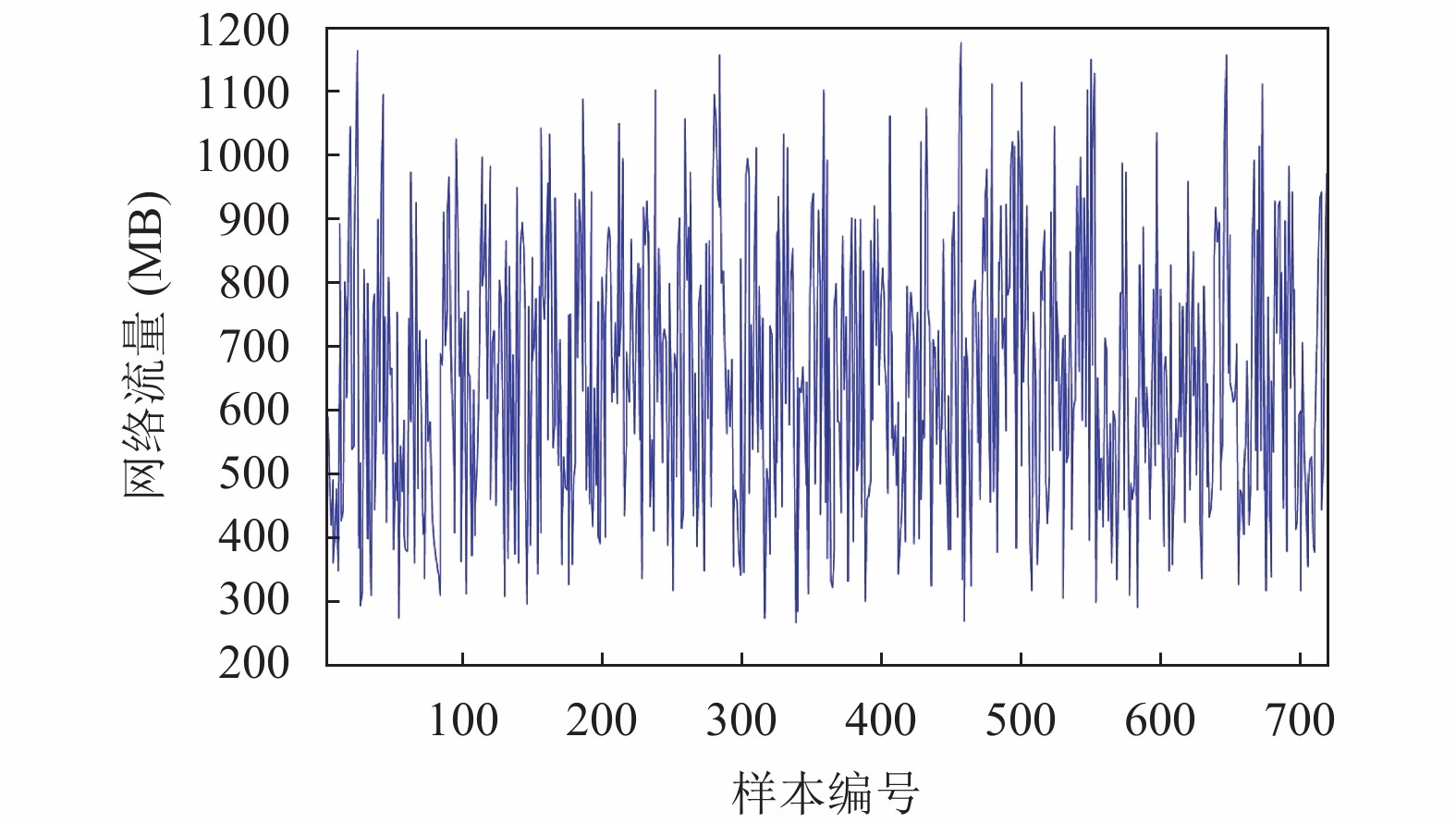
|
图 2 实验流量数据样本 |
本次仿真实验共分为两组, 分别为1步预测仿真和3步预测仿真. 首先对样本群进行相空间重构, 采用C-C法对流量样本进行处理, 求得最优的重构时延τ=2, 嵌入维m=10, 完成重构后将前800条样本输入LSSVM训练, 并采用改进PSO算法进行参数寻优. 得到最优参数为: γ=102.83,σ=1.35, 最终构建针对SDN网络流量的预测模型. 在经过前800条样本的训练后, 对后200条验证样本进行预测对比, 其中1步预测实验结果如图3所示.
观察图3(a)中预测结果跟踪曲线可以发现, 在1步预测仿真实验中, 基于改进PSO-LSSVM的预测模型表现出了良好的预测精度, 各预测值与真实值拟合程度高, 预测结果跟踪曲线与真实流量变化曲线基本重合, 证明该模型很好地模拟了SDN网络流量所具备的周期性和非线性变化特征, 具有可靠的泛化性能; 从图3(b)中可以看出, 预测结果的偏差十分稳定, 且均在狭小范围内波动. 在200次的预测结果与真实数据的比对中, 167次预测结果的相对误差小于6 MB, 其中更有94次相对误差小于2 MB, 而误差超过8 MB仅有9次, 且所有预测误差均在10 MB以内, 预测结果表现出了良好的精确性和稳定性.
网络流量预测模型需要真实反映网络流量变化规律, 其预测精度越高、提前量越大, 模型应用价值就越高. 1步预测仅能对时间序列中下一个临近点的流量进行预测, 并不能客观的验证模型的预测性能[21], 为了进一步考察本模型在网络流量多步预测方面的表现, 设计了3步预测仿真实验, 其结果如图4所示.
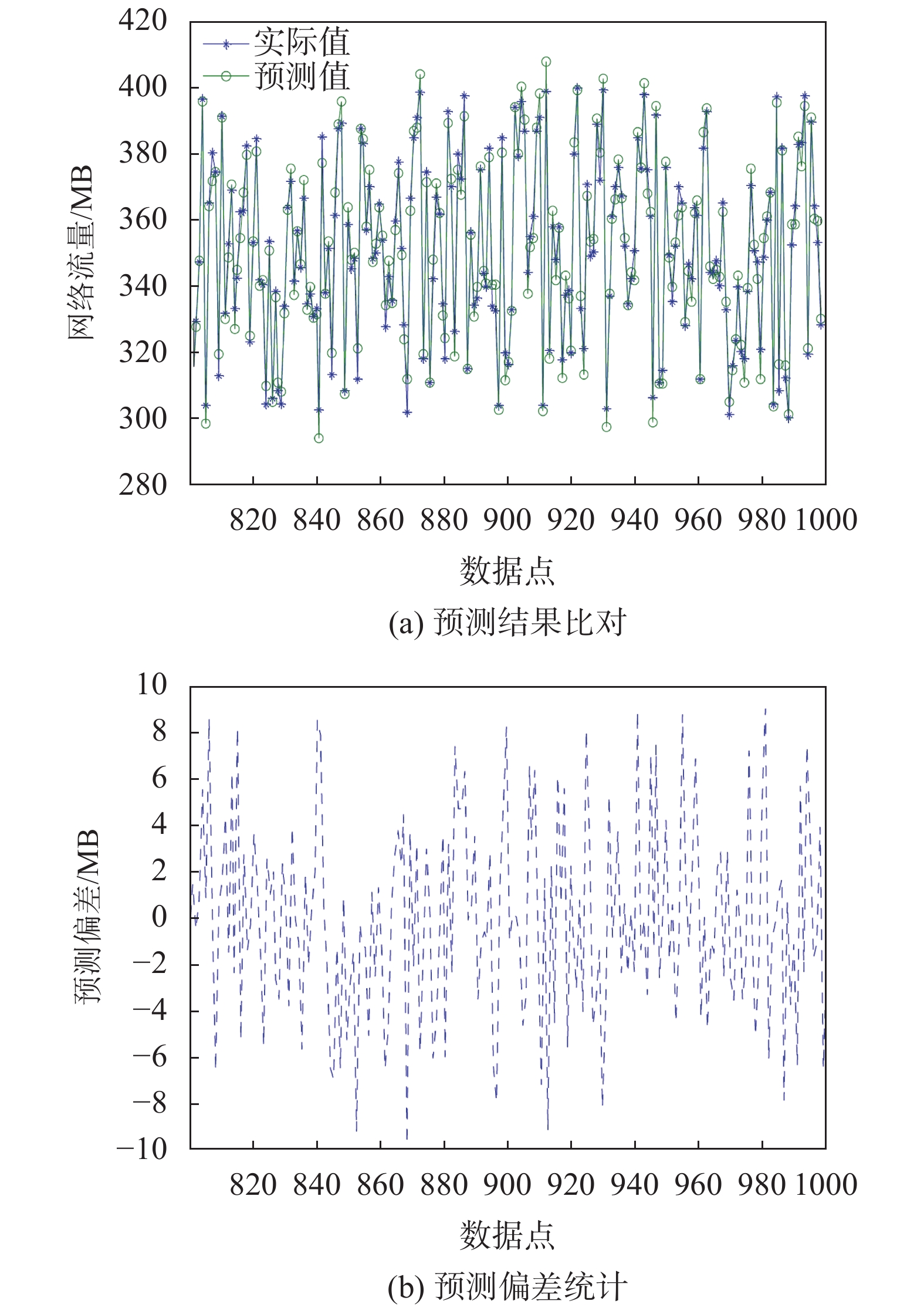
|
图 3 SDN网络流量1步预测实验结果 |
观察图4(a)可以发现, 在增加了预测提前量之后,模型对SDN网络流量变化的拟合性能有了一定程度的下降, 且图4(b)中的预测偏差也有所增大, 但预测质量整体上仍处于良好水平, 其中154次预测相对误差在20 MB以内, 仅有4次超过40 MB, 其中1次达到了最高的50.13 MB. 从整体来看, 误差波动范围稳定, 基本控制在10%以内, 预测曲线与实际流量曲线的波动方向吻合, 能够在实际应用过程中对网络流量监控工作提供可靠的参考.
为了对比分析预测模型的运行质量, 同时选取了BP神经网络(BPNN)、自回归滑动平均(ARIMA)和基于遗传算法的最小二乘支持向量机(GA-LSSVM)三种预测模型参与实验, 并选取相对平均误差(MPAE)和均方根误差(RMSE)两种指标对预测结果进行评价, 其计算公式分别为:
| $MPAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right|} \times 100{\text{%}} $ | (18) |
| $RMSE = \sqrt {\frac{{\displaystyle\sum\limits_{k = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{n}} $ | (19) |
使用以上3种网络流量预测模型对同组样本进行预测, 并将统计结果与本文提出的改进PSO-LSSVM模型的预测结果进行对比分析, 其统计结果如表1所示.
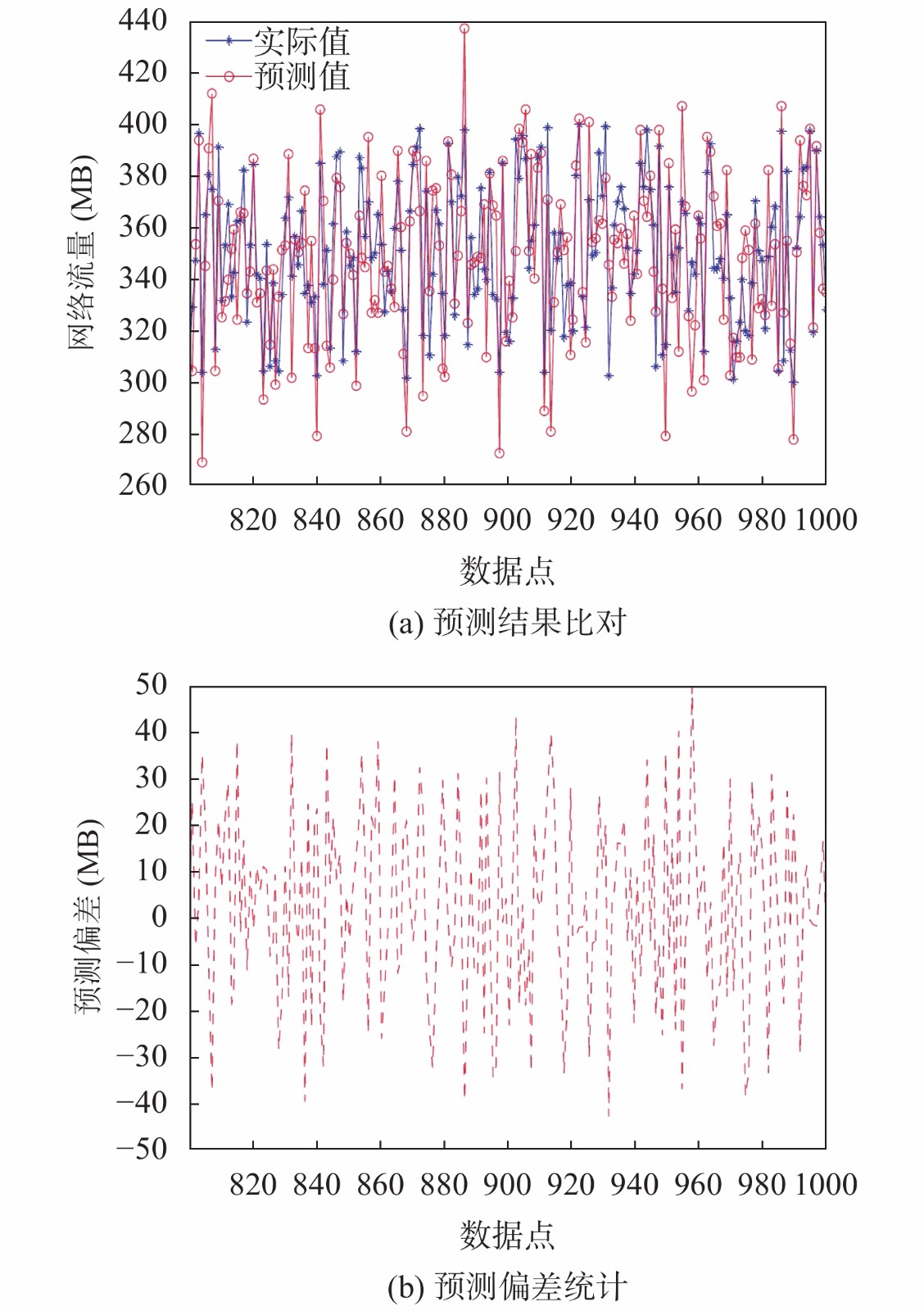
|
图 4 SDN网络流量3步预测实验结果 |
| 表 1 多模型预测结果统计信息 |
对比4种模型对SDN网络流量的预测统计数据可以看出, 相较于BPNN模型和ARIME模型, 改进后的PSO-LSSVM模型在1步与3步预测仿真实验中表现出明显优势, 其预测结果的拟合精度和误差控制水平均大幅领先, 这也证明了基于最小二乘向量机LSSVM技术构建的预测模型具有更好的泛化性能, 尤其适合针对大规模样本群体的分析与处理场合; 而与采用了同类型技术的GA-LSSVM模型相比, 本模型1步预测的质量依旧明显领先于前者, 这说明改进后的PSO算法对惯性权重和学习因子实施自适应动态调节后, 显著地提高了粒子的全局搜索能力, 更有效的避免了在局部极值问题, 从而获得了比遗传算法更加突出的参数寻优效果. 在3步预测仿真实验中, 本模型表现出的优势虽有所减少, 但仍要优于GA-LSSVM模型, 这表明随着预测步数(即预测提前量)的增加, SDN网络流量的非线性和时变特征对模型构成的干扰效应会持续放大, 从而导致所有模型的预测质量均会下降, 彼此之间的表现差异也会相对缩小, 这一规律在其余两种模型的预测结果中也得到了充分的体现.
5 结束语本文针对SDN网络流量预测问题展开研究, 首先提出对SDN网络流量时间序列进行混沌处理, 实现在多维相空间中的重构, 减少了网络流量的复杂性特征对预测模型造成的负面影响; 随后采用自适应方法对PSO算法中的惯性权重及学习因子进行动态调整, 显著改善了该算法的参数寻优能力, 并将其引入到LSSVM中, 最终构建出SDN网络流量预测模型. 通过仿真实验证明, 该模型与其他3种经典预测模型相比, 在预测精度和误差控制等方面具有明显的优势, 应用前景十分广泛.
| [1] |
Liu J, Li J, Shou G C, et al. SDN based load balancing mechanism for elephant flow in data center networks. Proceedings of 2014 International Symposium on Wireless Personal Multimedia Communications. Sydney, NSW, Australia. 2015. 486–490.
|
| [2] |
朱格, 李明政, 刘童, 等. 利用SDN实现可编程无线局域网多径接入管理. 计算机系统应用, 2019, 28(9): 125-132. DOI:10.15888/j.cnki.csa.007075 |
| [3] |
王逸兮, 余铮, 查志勇, 等. 基于改进SVM的电力企业信息系统异常检测方案的优化. 计算机与数字工程, 2020, 48(3): 567-570, 662. DOI:10.3969/j.issn.1672-9722.2020.03.013 |
| [4] |
Auld T, Moore AW, Gull SF. Bayesian neural networks for Internet traffic classification. IEEE Transactions on Neural Network, 2007, 18(1): 223-239. DOI:10.1109/TNN.2006.883010 |
| [5] |
叶德忠, 巫忠正, 蒋勇. 基于马尔可夫时变模型的流量数据挖掘. 软件, 2017, 38(9): 8-11. DOI:10.3969/j.issn.1003-6970.2017.09.002 |
| [6] |
Lu Y, Fu BC, Xi XF, et al. An SDN-based flow control mechanism for guaranteeing QoS and maximizing throughput. Wireless Personal Communications, 2017, 97(1): 417-442. DOI:10.1007/s11277-017-4512-9 |
| [7] |
李晓方, 王子磊, 奚宏生. 混合SDN的自适应流量估计方法. 计算机工程, 2016, 42(3): 103-110. DOI:10.3969/j.issn.1000-3428.2016.03.019 |
| [8] |
于静, 王辉. 基于组合模型的网络流量预测. 计算机工程与应用, 2013, 49(8): 92-95. DOI:10.3778/j.issn.1002-8331.1109-0531 |
| [9] |
李亦滔. 基于支持向量机的改进分类算法. 计算机系统应用, 2019, 28(10): 145-151. DOI:10.15888/j.cnki.csa.007080 |
| [10] |
房汉鸣, 税爱社, 汪辉, 等. 支持向量机动态多分类方法. 后勤工程学院学报, 2017, 33(2): 90-96. DOI:10.3969/j.issn.1672-7843.2017.02.015 |
| [11] |
王鸣, 孙奕鸣. 小波支持向量机的网络流量预测研究. 计算机仿真, 2012, 29(11): 198-201. DOI:10.3969/j.issn.1006-9348.2012.11.046 |
| [12] |
周向军. 基于最小二乘支持向量机的无线网络信道检测. 计算机系统应用, 2018, 27(5): 151-155. DOI:10.15888/j.cnki.csa.006339 |
| [13] |
Nguyen TTT, Armitage G. A survey of techniques for Internet traffic classification using machine learning. IEEE Communications Surveys & Tutorials, 2008, 10(4): 56-76. |
| [14] |
阳凯, 林海涛, 黎海雪. 基于SDN的流量控制算法综述. 通信技术, 2019, 52(4): 773-781. DOI:10.3969/j.issn.1002-0802.2019.04.001 |
| [15] |
Este A, Gringoli F, Salgarelli L. Support vector machines for TCP traffic classification. Computer Networks, 2009, 53(14): 2476-2490. DOI:10.1016/j.comnet.2009.05.003 |
| [16] |
Sequeira L, de la Cruz JL, Ruiz-Mas J, et al. Building an SDN enterprise WLAN based on virtual APs. IEEE Communications Letters, 2017, 21(2): 374-377. DOI:10.1109/LCOMM.2016.2623602 |
| [17] |
黄国权, 尤新华. 改进粒子群算法优化最小二乘支持向量机的网络流量混沌预测. 激光杂志, 2015, 36(3): 96-99. |
| [18] |
陈鸿星. 基于ELM-LSSVM的网络流量预测. 计算机工程与应用, 2015, 51(24): 73-77. DOI:10.3778/j.issn.1002-8331.1312-0119 |
| [19] |
李昆仑, 张亚欣, 刘利利, 等. 基于改进PCA和支持向量机的掌纹识别. 计算机科学, 2015, 42(S2): 146-150. |
| [20] |
Wang XD, Tian Y, Zhao M, et al. PNPL: Simplifying programming for protocol-oblivious SDN networks. Computer Networks, 2018, 147: 64-80. DOI:10.1016/j.comnet.2018.09.018 |
| [21] |
王雪松. 改进支持向量机的网络流量预测. 计算机系统应用, 2017, 26(3): 230-233. DOI:10.15888/j.cnki.csa.005668 |
 2021, Vol. 30
2021, Vol. 30



