2. 中原工学院 前沿信息技术研究院, 郑州 450007
2. Research Institute of Frontier Information Technology, Zhongyuan University of Technology, Zhengzhou 450007, China
高性能计算机是国家综合国力的重要体现, 对现代社会的科学研究、社会服务、经济活动而言, 已成为不可或缺的战略工具, 全球众多国家都极为重视高性能计算能力的建设与发展[1]. 基础数学函数库[2]作为处理器配套软件的重要组成部分,是高性能计算机平台上各领域应用软件开发必需的最基础、最核心的软件之一. 而基础数学库的实现与硬件平台密切相关, Intel、AMD等主流CPU厂商都推出了与其平台相对应数学库软件. 随着高性能计算需求的日益增大, 越来越多的应用开始部署在以申威处理器为代表的国产高性能计算平台上[3]. 申威1621处理器是一款具有我国自主知识产权的高性能处理器, 针对该处理器, 目前已经推出了与之对应的国产数学库软件, 并且做了相对应的优化, 达到了工程的需求, 其性能较之GNU的glibc数学库也有较大的优势.
从算法优化角度, 文献[4]在分析现有算法的基础上, 提出初等函数算法设计原则和两种算法设计模式, 使得主核函数的性能平均提高52.4%, 从核函数的性能平均提高75.3%, 并且精度与GNU总体保持一致. 文献[5]针对超越函数的实现繁琐易错、应用精度需求各异等问题, 提出并实现兼顾通用性和函数数学特性的可变精度超越函数算法. 该算法不仅能够生成常见超越函数的不同精度版本的函数代码, 且相对标准数学库超越函数具有性能优势.
从访存优化角度, 文献[6]为有效解决超越函数查表与多项式结合算法的“存储墙”问题, 提出基于数据表精简算法的超越函数访存优化方法, 使得函数性能平均提升55.06%. 文献[7]提出了一种基于访存指令的调度策略, 即将访存延迟有效地隐藏于计算延迟中, 平均提高函数性能16.08%. 文献[8]提出一种基于多级分层策略的寄存器分配策略, 合理地使用寄存器资源, 减少寄存器分配过程中产生的溢出, 将数学库中的函数性能提高6%以上. 文献[9]针对基础数学库中的寄存器分配特点, 利用最常用情况执行时间(Most-Case Execution Time, MCET)模型对经典的线性扫描寄存器分配算法进行了扩展, 将变量溢出过程分配到非常用路径上, 从而减少全局的寄存器溢出开销, 提高数学库的性能.
从SIMD向量化角度, 文献[10]结合三角函数、反三角函数、指数函数和对数函数研究出一种高效向量化算法, 并在申威26010处理器上完成扩展函数库实现, 在性能上与Intel VML数学库相比, 各函数的平均加速比均达到1.1以上. 文献[11]针对SIMD指令缺少和部分指令性能较低的问题, 提出了一种基于SIMD扩展指令的等价替换方法, 使得函数库性能提升13%左右. 文献[12]针对多数函数代码分支多和SIMD指令不完备的问题, 提出了向量数学库的向量化方法, 通过确定核心代码段、数据预处理过程向量化及指令向量化3个步骤, 使exp, pow, log10等典型函数的性能平均提高了24.2%. 文献[13]提出一种SIMD对齐的优化方法, 并采用一套系统的方法来处理绝对地址和相对地址访存方案, 与数学函数的非对齐存储器访问方案相比, 提升函数性能22.3%. 文献[14]提出一种向量寄存器部分数据重用的方法, 利用向量寄存器的部分元素来减少寄存器压力、冗余计算和内存访问, 与打包解包方法相比, 该方法使得函数性能平均加速14.19%.
文献[15]从基本块向量化、指令替换、访存、指令流水线等多个方面展开优化, 在保证数学库精度的同时, 有效提高了函数的性能.
以上文献提出的优化方法都对基础数学函数库性能有一定的提升, 但是还没有文献针对rfpcr和wfpcr指令作出优化处理. 在现版本基础函数库的实现中, tan、cot、remainder、fmodf、lround、modf、remquof、trunc等函数都使用了rfpcr指令和wfpcr指令, 该指令会导致流水线中断, 严重降低了函数库的性能. 因此本文在分析每个函数功能和指令特性后提出指令段功能等效替换方法, 提升函数性能.
本文第1节详细介绍指令替换方法; 第2节给出实验结果及分析; 最后对全文进行总结.
1 指令段替换方法在流水线技术中, 指令之间的相关性会在流水线中引起冲突, 冲突会导致流水线阻塞, 而流水线阻塞会降低流水线的效率[16]. 除了指令之间的相关性会导致流水线的阻塞, 还有一些特殊的指令由于指令的功能需求, 会直接阻断流水线, 比如rfpcr和wfpcr指令. 浮点控制寄存器(Floating-Point Control Register, FPCR)是浮点运算控制和状态寄存器, 其内容用于控制浮点运算的舍入方式、异常屏蔽等, 并记录浮点运算的异常状态. rfpcr指令的功能是读浮点控制寄存器的值, wfpcr指令向浮点控制寄存器写入新值.
当译码器识别出rfpcr指令时, 为保证rfpcr指令获得浮点控制寄存器的最新内容, rfpcr指令进入浮点指令队列发射的条件之一是前面的所有指令已执行完毕并退出流水.
当译码器识别出wfpcr指令时, 为保证wfpcr指令修改FPCR寄存器后能影响后继的浮点指令, 在指令流水线的发射站台设置一位CSR记分板, wfpcr指令从指令队列发射的条件之一是该记分板位已被清除, 该指令发射时, 设置该记分板位为“1”, 禁止发射队列发射后继的指令, 直到wfpcr指令完成并退出后, 清除该记分板位.
在申威基础数学库的实现中, rfpcr和wfpcr会与移位、加减计算等指令组成一个指令段, 指令段的主要功能是使得计算指令在向零舍入模式下执行. 图1是指令段伪代码.
在申威1621处理器中, 默认的舍入模式是就近舍入. 为了实现在向零舍入模式下执行计算指令, 需要在计算前用wfpcr指令将舍入模式修改为向零舍入, 即向FPCR寄存器中写入新值, 该值的舍入模式控制位为向零舍入, 计算完成后再用wfpcr指令将舍入模式还原.

|
图 1 指令段伪代码 |
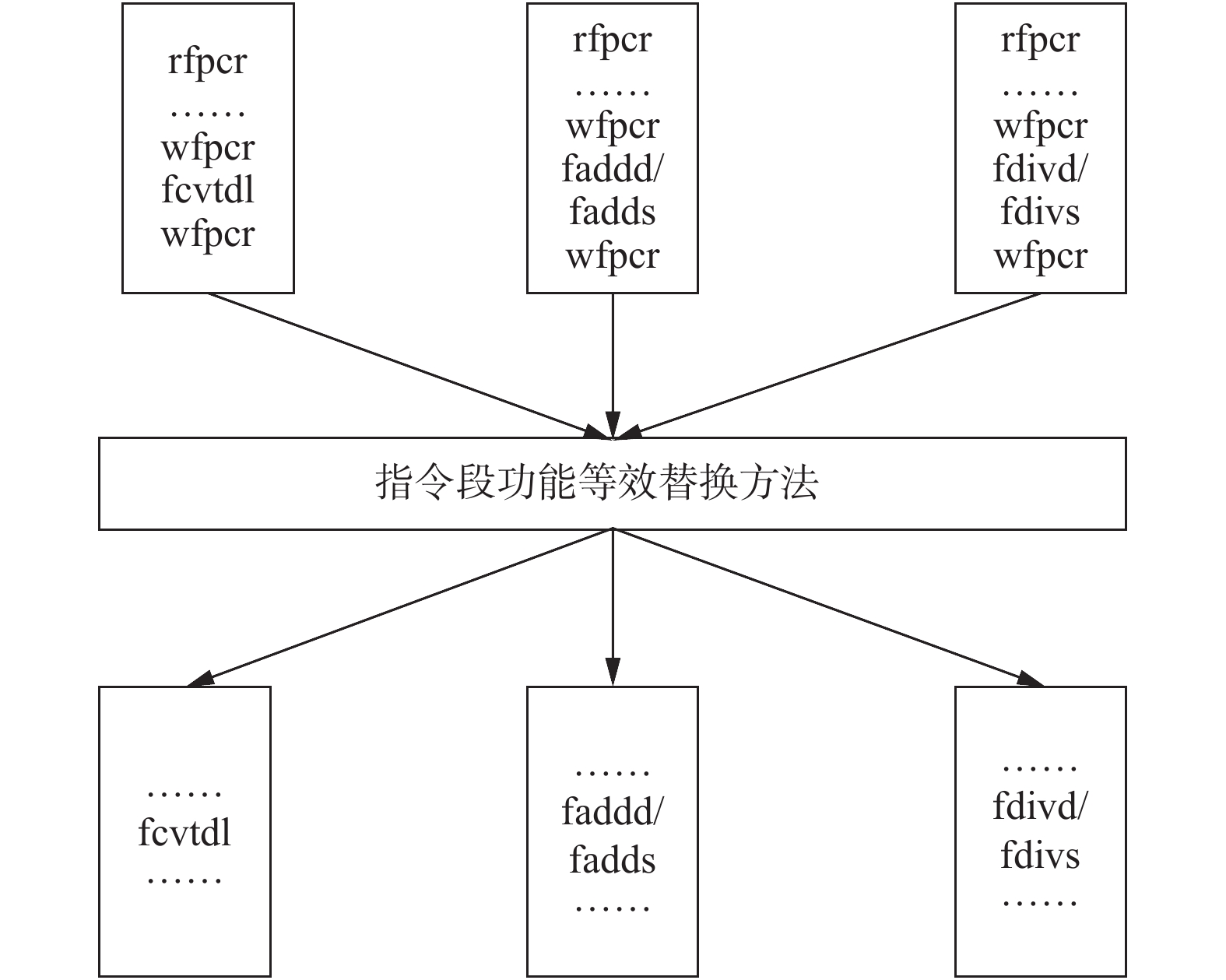
在有需要实现上述指令段功能的函数中, 计算指令有3种, 分别是浮点转整数指令(fcvtdl)、加法指令(faddd/fadds)和除法指令(fdivd/fdivs). 如图2所示, 本文在不改变这些指令段正确性的前提下, 使用等效的方法实现相同的功能. 在执行完上述3种计算指令后, 会得出一个值并被写入到寄存器中. 所谓功能等效替换方法是指在不使用rfpcr和wfpcr指令的前提下, 结合每个计算指令的功能和特性, 使用另外一种方法得出计算结果, 该结果与原版基础数学函数库实现的方法所计算出的值一致.
|
图 2 功能等效替换方法示意图 |
1.1 浮点小数取整法
对于浮点小数来说, 浮点数的尾数包含浮点数的整数部分和小数部分, 且整数部分所占的位数与指数大小有关. 对于双精度浮点数, 若浮点数指数的十进制数值是n, 则小数部分占尾数的[0,51–n]位, 整数部分占尾数的[(51–n)+1,51]位. 在十进制数中, 若将小数点后面的数全部变为0, 则小数就变成了一个整数. 同样对于二进制数而言, 将小数点后面的位全部置为0, 也就是将双精度浮点数的[0,51–n]位置0, 则该二进制浮点数就变成了一个浮点整数, 也即实现浮点小数取整化. 其具体的步骤如下:
假设是对双精度浮点数f1进行浮点小数取整化,
Step 1. 将f1对应的二进制数传给t1; 生成一个二进制数t2, 其值为0x7FF0000000000000, 即52到63位为1, 其他位为0.
Step 2. 将t1与t2进行逻辑与运算, 右移52位后, 减去1023, 得到f1指数的十进制数值n.
Step 3. 将52减去n, 计算出浮点数尾数的小数部分占据的位数.
Step 4. 生成一个二进制数t3, 其值的0到(52–n)位为0, 其他位为1.
Step 5. 将t3与t1进行逻辑与运算, 使得浮点数尾数中的小数部分为0; 再将t1的值传给f1.
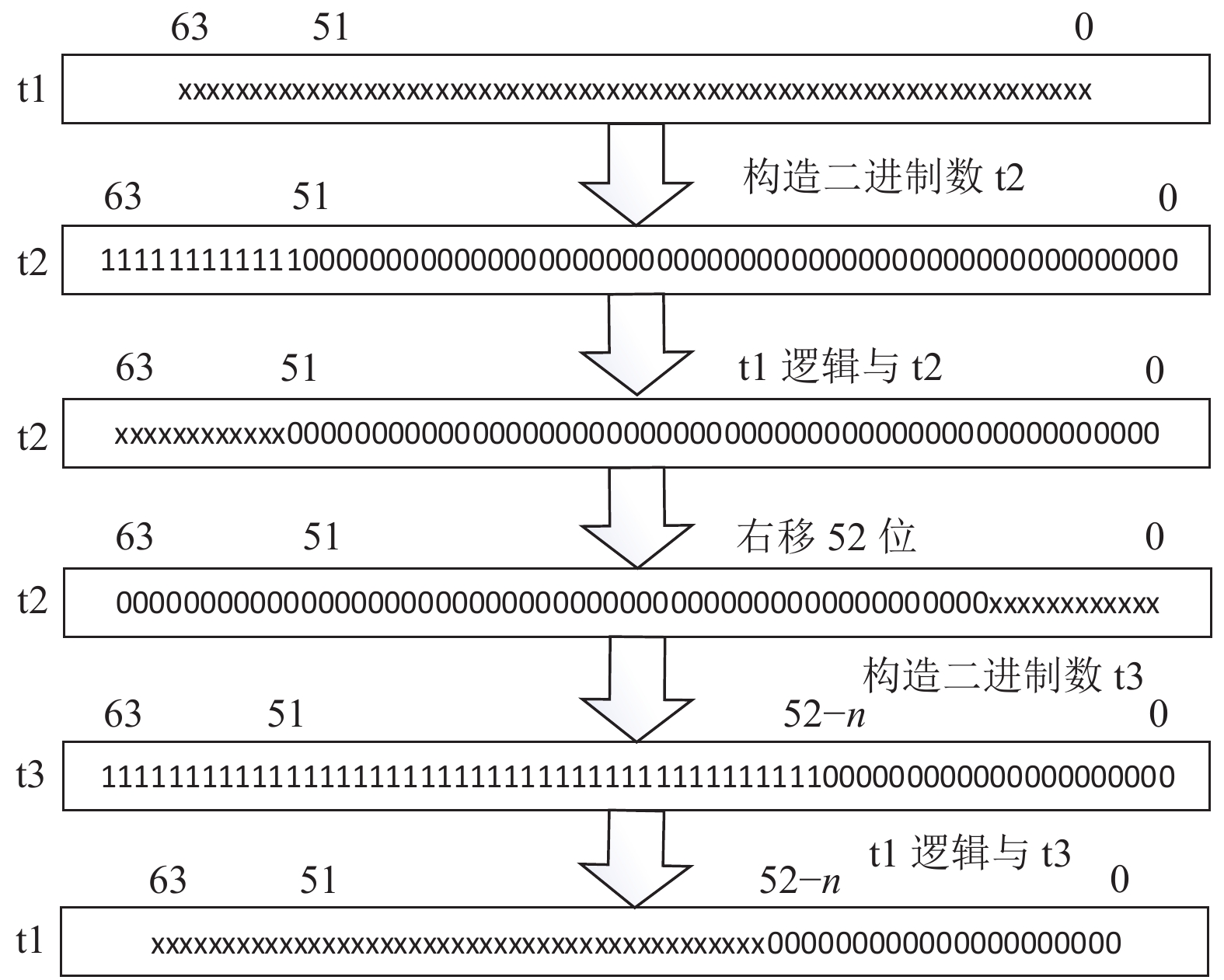
图3是按照上述思路, 对浮点数f1(浮点数对应的二进制数每一位用x表示)进行浮点小数取整化的实现过程.
|
图 3 利用移位、逻辑与指令完成浮点小数取整化的流程图 |
对应的汇编代码如下:
fimovd $f1,t1
ldi t2,2047(zero)
sll t2,52,t2//对应Step 1
and t1,t2,t2
srl t2,52,t2
ldi t12,1023(zero)
subl t2,t12,t2//对应Step 2
ldi t4,52(zero)
subl t4,t2,t2//对应Step 3
ldi t3,0(zero)
ornot zero,t3,t3
sll t3,t2,t3 //对应Step 4
and t3,t1,t1
ifmovd t1,$f1//对应Step 5
指令说明: fimovd将双精度浮点数从浮点寄存器传送到整数寄存器; ldi为立即数装载指令; sll为逻辑左移指令; bic实现逻辑与非运算; and为逻辑与指令; srl为逻辑右移指令; ornot为逻辑或非指令; subl为长字减指令; ifmovd将整数寄存器中长字整数按照双精度浮点传送到浮点寄存器.
fcvtdl指令将双精度浮点数转化成长字, 且依据浮点控制寄存器中的舍入方式控制位来选择舍入方式. 本文在查阅申威1621的指令集手册后, 发现在硬件的设计上, fcvtdl_z指令实现了向“0”舍入模式下, 将双精度浮点数转换成长字的功能. 所以直接用fcvtdl_z指令即可实现rfpcr、wfpcr和fcvtdl指令段的功能等效替换.
但是该指令存在一个问题, 若双精度浮点数是一个浮点小数, 而不是浮点整数, 那么在转换后, FPCR寄存器的非精确异常控制位会被置1, 从而产生一个非精确异常问题. 因此使用浮点小数取整法, 提前将浮点小数转换为浮点整数, 即可解决fcvtdl_z指令产生的非精确异常问题.
1.2 终点判断法申威1621处理器按照IEEE-754浮点标准[17]设置了4种舍入模式, 分别是就近舍入、向零舍入、向负无穷大舍入和向正无穷大舍入, 其中就近舍入即0舍1入. 在十进制数运算的四舍五入中, 若有效位后面第一位的值小于5, 则舍入的结果与向零舍入的结果相同; 若有效位后面第一位的值大于5, 则舍入的结果会比向零舍入的结果大1. 0舍1入法与其类似. 在二进制数运算中, 有一个对阶的过程, 如果参与计算的两个值阶码不同, 就需要将阶码小的值的阶码左移, 使其阶码与另一个阶码较大的数相同, 同时尾数需要右移. 在尾数右移时, 若被移去的最高数值位为0, 则舍入, 此时舍入的结果与向零舍入的结果相同; 若被移去的最高数值位为1, 则在尾数的末位加1, 此时舍入结果的二进制数值比向零舍入结果的二进制数值大1.
终点判断法是在默认舍入模式下, 一条运算指令执行结束并且计算结果写入寄存器后, 根据不同的计算指令选择不同的判断方法决定计算结果. 按照四则运算指令分类, 终点判断法可以分为和判断法、差判断法、乘判断法和除判断法.
下面分别以加法指令faddd/fadds和除法指令fdivd/fdivs说明终点判断法.
1) faddd/fadds指令
Faddd/fadds指令实现的是浮点数加的功能, 并将相加的结果舍入到指定的精度, 舍入方式根据浮点控制寄存器中的舍入方式控制位来选择. 其中faddd指令实现双精度浮点数加, fadds指令实现的是单精度浮点数加. Faddd指令和fadds指令的结果对本文的替换方法没有影响, 因此本文基于faddd指令分析替换方法.
和判断法依据被移去的最高数值位的值决定运算的结果. 当最高数值位为0时, 则和不变. 当最高数值位为1时, 则将和的二进制数减1. 以加法运算语句faddd $f1, $f2, $f3为例, 其实现流程如图4所示.

|
图 4 和判断法实现流程图 |
2) fdivd/fdivs指令
Fdivd/fdivs指令实现的是浮点数除法的功能, 商舍入到指定精度, 舍入方式根据浮点控制寄存器中的舍入方式控制位来选择. 其中fdivd指令实现双精度浮点数除, fdivs指令实现的是单精度浮点数除. Fdivd指令和fdivs指令的结果对本文的替换方法没有影响, 因此本文基于fdivd指令分析.
在十进制运算的四舍五入中, 若是“四舍”, 则舍入的结果比未舍入的结果小; 若是“五入”, 则舍入的结果比未舍入的结果大. 同样在二进制运算的0舍1入中, 若是“0舍”, 则舍入的结果比未舍入的结果小; 若是“1入”, 则舍入的结果比未舍入的结果大.
商判断法依据回乘商的方法决定运算的结果. 回乘商是指在不进行舍入情况下, 将商与除数相乘, 得到一个积. 若商是“0舍”后得出的结果, 则积应比除法语句中的被除数小, 此时商的值不变. 若商是“1入”后得出的结果, 则积应比除法语句中的除数大, 此时商对应的二进制值减去1.
以除法运算语句fdivd $f11,$f12,$f13为例, 其替换的具体过程如下:
Step 1. 就近舍入下, 执行除法计算, 得到商.
Step 2. 将商与被除数相乘得到积, 这个积不做任何舍入操作.
Step 3. 将积与除数相减, 得到一个差.
Step 4. 判断差是否小于0. 若差小于0, 则商值不变. 若差大于0, 则将商对应二进制数减1.
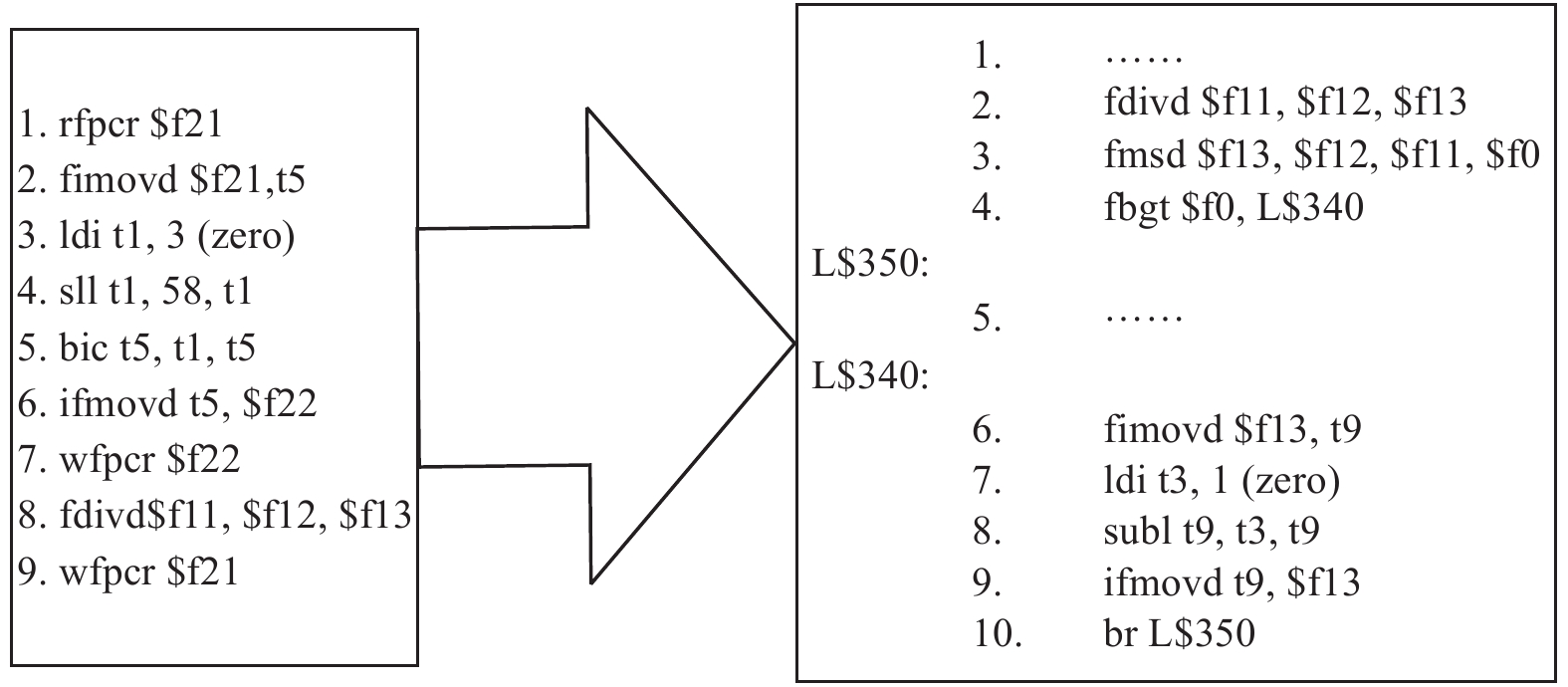
图5中, 左图是采用rfpcr和wfpcr指令设置舍入模式方法实现的指令段, 右图是采用商判断法实现的指令段.
|
图 5 商判断法实现的指令段替换 |
指令说明: fmsd为双精度浮点乘减指令, f13与f12相乘再减去f11, 最后结果写入f0, 且只对最终结果进行舍入; fbgt为浮点数大于“0”转移指令.
终点判断法实现的是在就近舍入模式下计算出向零舍入结果的功能, 替换了原版使用rfpcr和wfpcr指令修改舍入模式的方法, 以此提高性能. 其中商判断法是在分析就近舍入和向零舍入的关系后提出的方法, 和判断法是在分析就近舍入和向零舍入的关系以及就近舍入的实现方式后提出的方法. 由于申威1621处理器的舍入模式是按照IEEE-754浮点标准实现的, 因此终点判断法不仅可以应用于申威1621处理器, 对于其他满足IEEE-754浮点标准的处理器都可适用. 同时该方法主要针对四则运算提出的, 本文目前提出了和判断法和商判断法, 同样对于减法运算和乘法运算也可以应用终点判断法实现在就近舍入模式下计算出向零舍入结果的功能, 相对应的方法可以命名为差判断法与积判断法.
2 实验及结果分析为了验证本文方法的有效性, 以申威1621处理器为实验平台. 实验平台相关配置信息如表1所示.
| 表 1 申威1621实验平台 |
实验从正确性和性能两方面进行测试. 正确性测试用Glibc测试套件分别对替换前和替换后的计算结果进行对比; 由于部分函数需要替换多种指令, 因此性能测试综合3种替换指令计算对函数的整体性能提升. 性能提升的计算公式如下:
性能提升=(替换前节拍−替换后节拍)/替换前节拍×100%
2.1 正确性测试本文用glibc测试套件作为测试用例, 替换前与替换后的计算结果保持一致. 测试结果表明, 替换后与替换前的功能是等效的.
2.2 性能测试本文性能测试通过rtc (读计时器TC)指令计算被测函数的运行节拍数来衡量性能的好坏. 为保证性能测试能够覆盖函数的主要分支, 主要采用0~1区间内均匀分布的随机浮点数作为测试数据集, 测试基础函数库运行两百次的节拍数. 为了减小偏差较大的测试数据对性能测试结果的影响,采用4D检测法[18]对函数运行节拍数进行处理并求算术平均值. 测试结果如图6所示. 图7是每个函数的性能提升百分比.
图6的测试结果表明, 本文提出的指令段功能等效替换方法有效地解决了基础数学函数库中因rfpcr和wfpcr指令导致的断流水问题, 与替换前的函数性能相比, 替换后的每个函数性能都有不同程度的提升.
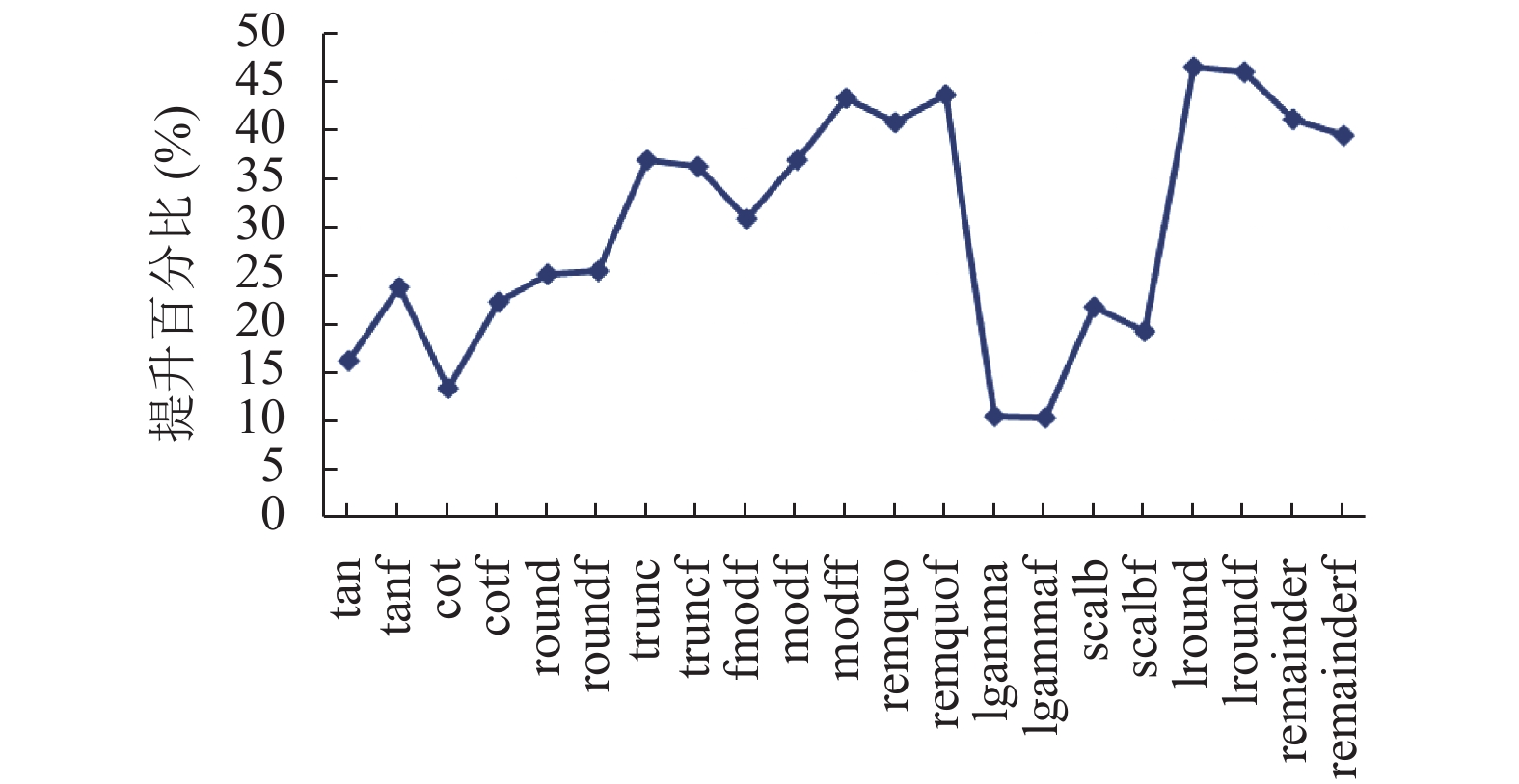
从图7的结果来看, 可以将性能提升百分比分为两种情况:
1) lround、remquo和remainder等函数性能提升百分比较高. 在这些函数中, 同时应用了浮点小数取整法和终点判断法, 并且remquo和remainde函数多次应用两种替换方法, 使得性能提升比较明显.
2) tan、cot和lgamma等函数性能提升百分比较低. 这是因为tan和cot函数只应用了终点判断法中的和判断法, 并且只替换了一次. lgamma函数应用了一次浮点小数取整法且多次应用了终点判断法, 但是该函数分支较多, 替换指令都处于不同的分支上, 因此性能提升较低.

|
图 6 替换前后性能对比 |
|
图 7 性能提升百分比 |
综合以上两种情况的分析, 可以得出性能提升效果不同的主要原因有以下几种: 1)部分函数需要应用两种替换方法, 部分函数只需要应用一种替换方法. 2)有的函数需要替换多次, 有的函数只需替换一次; 3)有的替换指令分布在热路径[19]的分支上, 有的替换指令是在函数较少使用的路径上.
3 结论与展望基础数学库在科学计算中发挥着举足轻重的作用, 其性能直接影响着科学计算程序的执行效率. 关于现版本国产申威基础函数库因rfpcr、wfpcr指令和计算指令组成的指令段导致的流水线中断问题, 本文提出指令段功能等效替换方法. 针对fcvtdl指令提出了浮点小数取整化方法, 针对faddd/fadds指令和fdivd/fdivs指令提出了终点判断法. 实验结果表明, 本文提出的方法有效的解决了rfprc和wfpcr指令断流水问题, 使函数性能平均提升27.83%. 下一步将充分利用流水线的硬件特性, 深度挖掘流水线的性能优势, 对指令流水线进行深入优化, 进一步提高函数性能.
| [1] |
郑晓欢, 陈明奇, 唐川, 等. 全球高性能计算发展态势分析. 世界科技研究与发展, 2018, 40(3): 249-260. |
| [2] |
许瑾晨, 郭绍忠, 黄永忠, 等. 浮点数学函数异常处理方法. 软件学报, 2015, 26(12): 3088-3103. DOI:10.13328/j.cnki.jos.004814 |
| [3] |
刘昊, 刘芳芳, 张鹏, 等. 基于申威1600的3级BLAS GEMM函数优化. 计算机系统应用, 2016, 25(12): 234-239. DOI:10.15888/j.cnki.csa.005456 |
| [4] |
周蓓, 黄永忠, 许瑾晨, 等. 面向申威异构众核处理器的初等函数算法研究. 信息工程大学学报, 2020, 21(2): 159-163, 171. DOI:10.3969/j.issn.1671-0673.2020.02.007 |
| [5] |
郝江伟, 郭绍忠, 夏媛媛, 等. 可变精度超越函数算法设计. 计算机科学, 2020, 47(8): 71-79. |
| [6] |
孟虹松, 郭绍忠, 许谨晨, 等. 基于数据表精简算法的超越函数访存优化方法. 信息工程大学学报, 2019, 20(3): 328-334. DOI:10.3969/j.issn.1671-0673.2019.03.013 |
| [7] |
许瑾晨, 郭绍忠, 黄永忠, 等. 面向异构众核从核的数学函数库访存优化方法. 计算机科学, 2014, 41(6): 12-17. DOI:10.11896/j.issn.1002-137X.2014.06.003 |
| [8] |
郭正红, 郭绍忠. 基础数学库中的层次结构寄存器分配策略. 计算机工程, 2012, 38(24): 266-268, 273. DOI:10.3969/j.issn.1000-3428.2012.24.063 |
| [9] |
郭绍忠, 郭正红, 王磊. 基础数学库中的MCET寄存器分配方法. 计算机应用与软件, 2013, 30(3): 291-293. DOI:10.3969/j.issn.1000-386x.2013.03.077 |
| [10] |
曹代, 郭绍忠, 张辛. 基于申威26010处理器的扩展函数库实现与优化. 计算机工程, 2017, 43(1): 61-66, 71. DOI:10.3969/j.issn.1000-3428.2017.01.011 |
| [11] |
郭绍忠, 许瑾晨, 陈世淼. SIMD优化中的指令等价替换实现方法. 河南省计算机学会2011年学术年会论文集. 信阳, 中国. 2011. 1–5.
|
| [12] |
周蓓, 黄永忠, 许瑾晨, 等. 向量数学库的向量化方法研究. 计算机科学, 2019, 46(1): 320-324. DOI:10.11896/j.issn.1002-137X.2019.01.050 |
| [13] |
Wang L, Zhang CY, Huang YZ. An optimization approach for SIMD alignment in mathematical functions. In: Wu YW, eds. Advances in Computer, Communication, Control and Automation. Berlin Heidelberg: Springer, 2011. 37–43.
|
| [14] |
Wang L, Zhang CY, Huang YZ, et al. Partial elements reuse of vector register in SIMD mathematical functions. International Journal of Advancements in Computing Technology, 2012, 4(1): 327-335. DOI:10.4156/ijact.vol4.issue1.38 |
| [15] |
曹代, 郭绍忠, 张辛. 某国产平台数学库优化技术研究. 信息工程大学学报, 2017, 18(4): 470-474, 497. DOI:10.3969/j.issn.1671-0673.2017.04.017 |
| [16] |
胡伟武, 汪文祥, 吴瑞阳, 等. 计算机体系结构. 2版. 北京: 清华大学出版社, 2017.
|
| [17] |
Kahan W. Lecture Notes on the Status of IEEE Standard 754 for binary floating-point arithmetic. Lecture Notes on the Status of IEEE, 1996: 18–19.
|
| [18] |
许瑾晨, 黄永忠, 郭绍忠, 等. 一个浮点数学函数库测试平台. 软件学报, 2015, 26(6): 1306-1321. DOI:10.13328/j.cnki.jos.004589 |
| [19] |
郭正红, 郭绍忠, 许瑾晨, 等. 异构多核平台下基础数学库寄存器分配方法. 计算机应用, 2014, 34(S1): 86-89. |
 2021, Vol. 30
2021, Vol. 30



