第5代移动通信技术(fifth-Generation, 5G)是继4G之后,为了满足智能终端的快速普及和移动互联网的高速发展而正在研发的下一代无线移动通信技术^[1]. 目前, 国内外正在对5G移动通信技术进行研究^[2-5]. 5G不仅为我们带来了更好的宽带体验, 也将对电力行业产生深远的影响^[6-10]. 其中, 智能电网作为5G与电力行业交叉融合下的一项典型应用, 正在快速发展^[11-13].

作为电力系统的一项重大创新, 智能电网方便了电力系统的管理, 在很大程度上能够提升电力系统的服务质量. 但是, 电力网络中的传感器及其他接入设备的增多, 将给电力系统带来了较大的负担. 为了向用户提供源源不断、质量合格的电能, 要求电力系统具有很高的稳定性和可靠性^[14,15].

目前, 很少有对智能电网稳定性预测的相关研究, 但有许多针对电力系统稳定性分析的研究可供参考. 隐形梯形积分法是电力系统暂态稳定性分析中的最基本的数值计算方法之一, 文献[16]通过采用隐形梯形积分法得出系统最大相对摇摆角曲线图, 进而去判定系统的暂态稳定性. 文献[17]运用电力系统动态等值分析原理,以耦合特性分析为切入点研究电力系统稳定性分析方法, 但该方法不能较好的适应于非线性系统. 文献[18]针对该问题, 提出了一种适合非线性复变系统的综合动态等值法来评估电力网络的静态电压稳定性. 元件参数也是影响系统稳定性的重要因素之一, 文献[19]综合运用摄动原理、轨迹灵敏度方法、参数灵敏度分析方法研究了同步发电机、调速器、励磁系统、主要输电线路和变压器等参数对电网暂态稳定性的影响. 除了以上的数值分析方法, 文献[20]从动力学角度出发, 将电力网络的非线性动力学方程和复杂网络相结合来研究电力网络的稳定性.

在5G时代, 机器学习和深度学习赋予了这个社会“智能”, 这些概念自提出以来就得到了广泛的关注, 并且出现了多方面的应用. 文献[21]使用机器学习前沿算法XGBoost算法对电力系统暂态稳定性问题进行建模, 并将模型输出进行概率化,以评估模型预测的可靠程度. 分布式智能电网(Decentralized Smart Grid, DSG)是针对存在弹性节点的电力网络所提出的新技术, 陈旭等人为了分析DSG的系统稳定性,应用具有代表性的6种机器学习分类模型, 结合电力系统安全性、稳定性、经济性3个方面的需求测试了各分类模型对DSG系统稳定性预测的效果^[22], 然而由于电力数据庞大且参数众多, 简单的机器学习模型并不能满足对电力网络准确预测的要求. 因此, 本文提出了一种基于卷积神经网络的智能电网稳定性预测算法, 首先对从智能电网中采集到的数据进行处理, 之后将其输入到CNN模型中, 经过不断的迭代运算, 最终得到一个电力网络稳定性预测模型. 经过仿真验证, 该模型对于智能电网稳定性预测有较高的准确率.

1 基于CNN的智能电网稳定性预测

有关机器学习的各种算法例如决策树, 随机森林, SVM (支持向量机), KNN (最近邻算法)在电力系统中都有广泛的应用. 在这些传统的机器学习算法上, 虽然能够得到对电力网络稳定性的预测, 但是需要耗费不小的精力去对特征进行处理, 并且预测的准确度不够高. 本章将介绍一种基于CNN的智能电网稳定性预测的算法, 该算法由两个卷积层, 两个池化层以及两个全连接层构成, 仿真验证了该算法有良好的准确率. 并且本文还比较了Adam^[23], RMSprop^[24]、SGD以及带有动量的SGD (MSGD)4种不同优化算法对于模型训练的影响^[25].

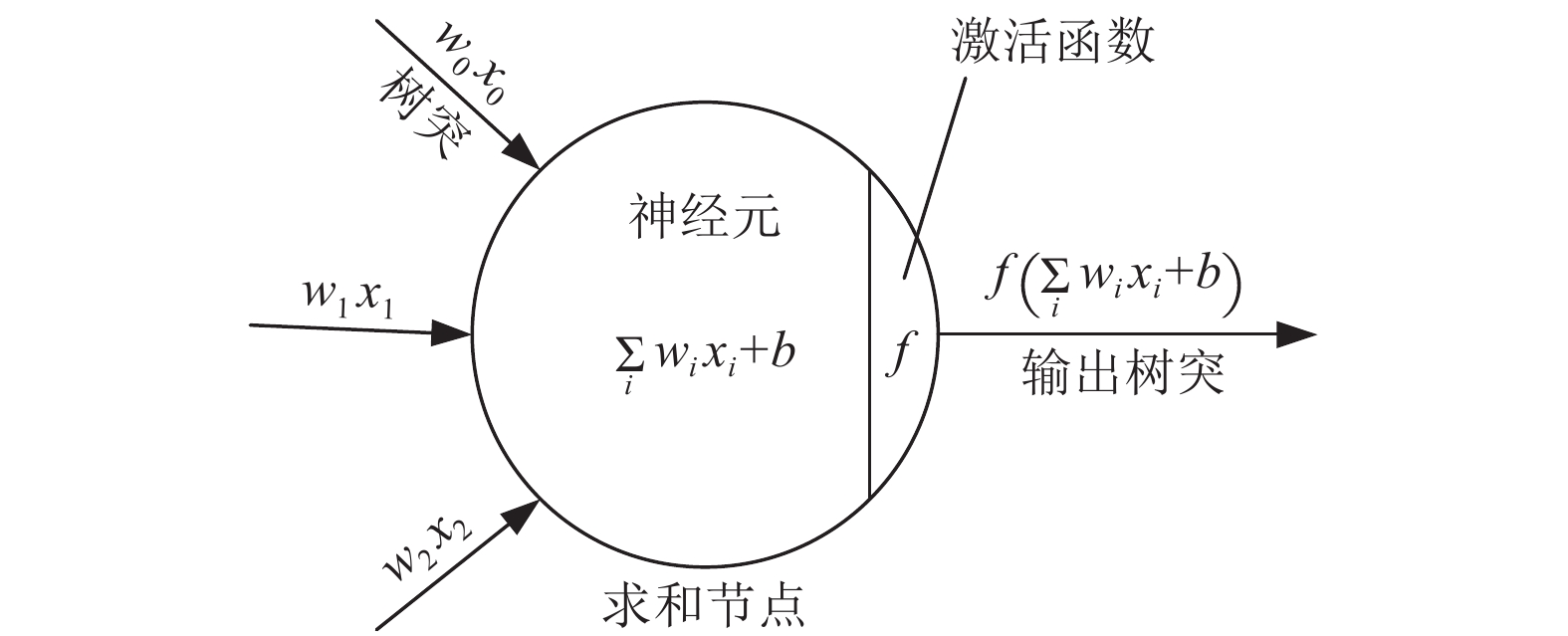
1.1 基于卷积神经网络的数学建模

本文采用的卷积神经网络的基本单位为神经元, 神经元的结构模仿了人类脑部的神经系统, 多个神经元相互连接而成一个神经网络. 一个基本的神经元由线性函数和激活函数两部分构成, 神经元的一侧接收输入信号, 经过线性函数的加权和加偏置处理, 将结果输入至激活函数, 之后由另一侧输出最终结果. 具有3个树突的单个神经元建模如图1所示.

神经元模型的公式为:

$h = f\left( {\sum\limits_i {{\rm{ }}{w_i}{\rm{ }}{x_i} + b} } \right)$

(1)

其中, ${w_i}$ 为线性函数的权重, $b$ 为偏置单元.

接着, 需要通过损失函数来优化模型, 损失函数的定义如下:

$L(w,b) = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{h^{(i)}} - {\rm{ }}{y^{(i)}}} \right)}^2}} $

(2)

其中, n为训练集的数量, $\mathop h\nolimits^{(i)} $ 为预测的输出, $\mathop y\nolimits^{(i)} $ 真实值.

单层的神经元构成的神经网络虽然简单, 但学习能力有限, 只能处理一些简单的线性分类任务, 具有很大的局限性. 而通过电力系统采集到的数据具有非线性和复杂的特点, 因此, 为了处理这些较为复杂的问题, 本章采用了引入非线性函数的CNN来进行智能电网稳定性的预测. 基于CNN的电力网络稳定性预测建模如图2所示.

卷积神经网络的工作原理就是通过不断地迭代去更新线性函数的权重和偏置单元, 使得损失函数的值最小, 同时得到一个较高的分类准确度. CNN具有参数共享和稀疏连接的功能, 这些功能模仿了生物视觉细胞只对局部视野或者特征敏感的特点.

基于CNN的智能电网稳定性预测模型通过卷积层自动提取与电网稳定性相关的12个特征, 再经过池化层对数据进行降维, 最后通过全连接层以及Softmax分类函数得到预测结果. 衡量CNN模型优劣的Accuracy值的范围在0到1之间, Loss值一般也在1以下. Accuracy值越低, Loss值越高, 则代表该模型的预测结果较差, 反之则表明模型越优.

1.2 基于CNN的智能电网稳定性预测

除了分析电网系统维护人员的不良行为或者误触行为, 依据电网产生的数据对其稳定性预测也是有效减少电力事故, 提高电力系统安全性的有效方法. 因此, 本文提出了基于CNN的智能电网稳定性预测模型, 该模型采用了kaggle上来自国外某电网系统采集到的68000个数据.

对于数据集, 由于各个特征值的范围不同, 因此需要对数据进行预处理. 预处理的目的是将数据的大小归一到一个统一的尺度内, 加快模型的训练速度, 提高分类精度. 数据预处理的方式通常有两种: 一种是标准化, 另一种是归一化. 归一化方法容易受到数据集结构不均衡的影响, 因此在这里采用标准化对数据进行预处理. 处理的步骤如下: 首先求取各个特征的数学期望 $E(\mathop X\nolimits_i )$ 和标准差 $\mathop S\nolimits_i $ , 然后根据以下公式得到标准化值:

$\mathop Z\nolimits_{ij} = \frac{{\mathop X\nolimits_{ij} - E(\mathop X\nolimits_i )}}{{\mathop S\nolimits_i }}$

(3)

其中, $\mathop X\nolimits_{ij} $ 是数据第i个特征的第j个值, $E(\mathop X\nolimits_i )$ 为第i个特征的均值, $\mathop S\nolimits_i $ 为第i个特征的标准差.

CNN 模型自动会提取电力网络中参与者的反应时间, 标准功率, 价格系数等12个特征, 并对其进行标准化, 为了能够将数据输入CNN模型中, 需要调整数据结构将其转化为与CNN输入矩阵大小一致的特征矩阵.

本节首先将经过标准化处理电力网络数据集后得到的12个特征转化为矩阵, 并输入CNN模型进行特征的提取. 其中, CNN模型中卷积层的权重更新如下:

(1)首先, 需要定义误差函数, 公式如下:

${\rm{ }}{C^N} = \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {{{\left( {y_k^n - {\rm{ }}p_k^n} \right)}^2}} } $

(4)

其中, $N$ 是样本的个数, K是样本的类别(即样本被分K类), $\mathop y\nolimits_k^n $ 表示第 $n$ 个样本 $\mathop y\nolimits_k $ 的第k维, $\mathop p\nolimits_k^n $ 是第 $n$ 个样本 $\mathop p\nolimits_k $ 网络输出的第k维.

最小化式(4)中的C可更新网络的权值, 使得CNN模型的输出预测值更加接近真实值.

(2)其次, 定义卷积层第l层的输出 $\mathop x\nolimits_j^l $ 为:

${\rm{ }}x_j^l = f\left( {\sum\limits_{i \in {\rm{ }}{M_j}} {{\rm{ }}x_i^{l - 1}} *{\rm{ }}k_{ij}^l + {\rm{ }}b_j^l} \right)$

(5)

其中, $\mathop x\nolimits_j^l $ 表示第 $i$ 层的第 $j$ 个特征, $f$ 是CNN的激活函数, $\mathop M\nolimits_j $ 表示输入数据的特征矩阵, $\mathop k\nolimits_{ij}^l $ 为 $l$ 层中连接输入的第 $i$ 类特征和输出的第 $j$ 类特征的卷积核, $\mathop b\nolimits_j^l $ 则为 $l$ 层中 $j$ 特征对应的偏置参数.

(3)误差灵敏度 $\mathop \delta \nolimits_j^l $ 可表示为:

$\delta _j^l = \beta _j^{l + 1}\left( {{f^\prime }\left( {\mu _j^l} \right)up\left( {\delta _j^{l + 1}} \right)} \right)$

(6)

其中, $\;\mathop \mu \nolimits_j^l {\rm{ = }}\mathop w\nolimits^l \mathop x\nolimits_j^{l - 1} + \mathop b\nolimits^l $ , $w$ 是权重, $b$ 为偏置单元. $l$ 层是卷积层, $l{\rm{ + }}1$ 是池化层, up是使 $l{\rm{ + }}1$ 层的矩阵的尺寸与 $l$ 层的尺寸保持一致的上采样操作, $\;\mathop \beta \nolimits_j $ 是卷积核 $\mathop k\nolimits_{ij}^l $ 中的值.

(4)接下来求误差函数对偏置 $\mathop b\nolimits_j^l $ 和卷积核 $\mathop k\nolimits_{ij}^l $ 的偏导:

$\frac{{\partial E}}{{\partial {b_i}}} = \sum\limits_{u,v} {{{\left( {\delta _j^l} \right)}_{u,v}}} $

(7)

$\frac{{\partial E}}{{\partial k_{ij}^l}} = \sum\limits_{u,v} {{{\left( {\delta _j^l} \right)}_{u,v}}} {\left( {q_i^{l - 1}} \right)_{u,v}} $

(8)

式(7)、式(8)是对 $l$ 层中所有的误差灵敏度进行求和, $(u,v)$ 是灵敏度矩阵中各元素的位置.

CNN模型中池化层的权值更新如下:

(1)池化层的第 $l$ 层的输出 $\mathop x\nolimits_j^l $ 可被定义为:

${\rm{ }}x_j^l = f\left( {down\left( {x_j^{l - 1}} \right) + {\rm{ }}b_j^k} \right)$

(9)

其中, $f$ 是激活函数, down是下采样操作, $\mathop b\nolimits_j^k $ 为偏置.

(2)令 $\;\mathop \mu \nolimits_j^l {\rm{ = }}\mathop w\nolimits^l \mathop x\nolimits_j^{l - 1} + \mathop b\nolimits^l $ , 误差灵敏度 $\mathop \delta \nolimits_j^l $ 可表示为

$ {{\displaystyle \delta }}_{j}^{l}=conv2\left( {{{ \delta }}_{j}^{l\rm+1},rot180\left( {{{ k}}_{ij}^{l+1}} \right),{{ full}}^{\rm{'}}} \right)·{{f}}^{{'}}\left( {{{ u}}_{j}^{l}} \right)$

(10)

池化层中误差函数C对偏置 $\mathop b\nolimits_j $ 的偏导等于卷积层中误差函数E对偏置 $\mathop b\nolimits_j $ 的偏导.

在神经网络中, 常用的非线性激活函数有Sigmoid函数、ReLU函数、tanh函数等, 其中Sigmoid函数和tanh函数随着自变量 $x$ 的增加, 其梯度会越来越小, 趋近于0, 这将导致迭代过程中权重的值更新缓慢, 因此, 为了解决梯度消失这个现象, 在CNN模型中采用ReLU函数作为激活单元. ReLU函数在 $x > 0$ 时梯度恒为1, 在 $x < 0$ 时恒为0, 结构简单并且计算成本较低, 速度较快, 为CNN模型的快速收敛提供了保障.

激活单元ReLU 函数的定义为:

$f(x) = \max (0,x)$

(11)

在CNN模型中, 不同的优化算法对电力网络稳定性预测的准确度不同, 并且不同的优化算法的收敛速度也不一致. 因此, 为了找到一个适合此模型的最优化算法以及比较不同优化算法之间的差异, 本文分别采用了Adam^[23], RMSprop^[24]、SGD以及带有动量的SGD(MSGD)4种不同优化算法对CNN模型进行优化^[25].

SGD算法即随机梯度下降算法, 它可以加快收敛的速度, 使Loss函数收敛到更小的最小值, 然而, 由于更新的频率比较快, SGD会产生梯度震荡, 导致收敛不稳定. 因此, 本文采用了加有动量的SGD算法对权重 $w$ 和偏置 $b$ 进行更新, 带有动量的SGD会在前一步的累计梯度上有一个跳跃, 之后加入了一个修正单元对其进行修正, 更新公式如下:

$\mathop v\nolimits_{dw} = \beta \mathop v\nolimits_{dw} + (1 - \beta )dw$

(12)

$\mathop v\nolimits_{db} = \beta \mathop v\nolimits_{db} + (1 - \beta )db$

(13)

$w = w - \alpha \mathop v\nolimits_{dw} $

(14)

$b = b - \alpha \mathop v\nolimits_{db} $

(15)

其中, $\;\beta $ 为超参数, 取值0.9左右, $\alpha $ 是学习速率, 取值0.01左右.

RMSprop优化算法采用指数加权平均, 旨在消除梯度下降中的摆动, 如果在某一处梯度值比较大, 则指数加权平均的结果就大, 反之则小, 以此来保证不同维度的梯度值都处在同一范围, 进而提高的稳定性. 它的更新公式如下:

$\mathop s\nolimits_{dw} = \beta \mathop s\nolimits_{dw} + (1 - \beta )\mathop {dw}\nolimits^2 $

(16)

$\mathop s\nolimits_{db} = \beta \mathop s\nolimits_{db} + (1 - \beta )\mathop {db}\nolimits^2 $

(17)

$w = w - \alpha \frac{{dw}}{{\sqrt {\mathop s\nolimits_{dw} + \varepsilon } }}$

(18)

$b = b - \alpha \frac{{db}}{{\sqrt {\mathop s\nolimits_{db} + \varepsilon } }}$

(19)

其中, $\;\beta $ 为超参数, 取值0.9左右, $\alpha $ 是学习速率, 取值0.01左右, $\varepsilon $ 是一个偏差修正单元, 取值一般为10⁻⁸.

Adam结合了Momentum梯度下降法和RMSprop算法, 它能加快模型的学习速度. Adam算法的参数更新公式如下:

$\mathop v\nolimits_{dw} = \mathop \beta \nolimits_1 \mathop v\nolimits_{dw} + (1 - \mathop \beta \nolimits_1 )dw$

(20)

$\mathop v\nolimits_{db} = \mathop \beta \nolimits_1 \mathop v\nolimits_{db} + (1 - \mathop \beta \nolimits_1 )db$

(21)

$\mathop s\nolimits_{dw} = \mathop \beta \nolimits_2 \mathop s\nolimits_{dw} + (1 - \mathop \beta \nolimits_2 )\mathop {dw}\nolimits^2 $

(22)

$\mathop s\nolimits_{db} = \mathop \beta \nolimits_2 \mathop s\nolimits_{db} + (1 - \mathop \beta \nolimits_2 )\mathop {db}\nolimits^2 $

(23)

其中, $\;\mathop \beta \nolimits_1 $ 和 $\;\mathop \beta \nolimits_2 $ 为梯度累计的指数, 是两个超参数, 在一般情况下 $\;\mathop \beta \nolimits_1 $ 取值0.9, $\;\mathop \beta \nolimits_2 $ 取值0.999, dw和bd是在一次batch上, 损失函数L关于权重 $w$ 和偏置 $b$ 的梯度值; $\mathop v\nolimits_{dw} $ 和 $\mathop v\nolimits_{db} $ 是算法在前 $t - 1$ 次迭代过程中的累计的梯度动量, 同样的, $\mathop s\nolimits_{dw} $ 和 $\mathop s\nolimits_{db} $ 也是算法前 $t - 1$ 次迭代过程中的累计的梯度动量.

算法在前期的迭代中会出现不小的偏差, 为了解决这个问题, 在公式中加入了偏差修正:

${\rm{ }}V_{dw}^c = \frac{{{\rm{ }}{v_{dw}}}}{{\left( {1 - \beta _1^t} \right)}}$

(24)

${\rm{ }}V_{db}^c = \frac{{{\rm{ }}{v_{db}}}}{{\left( {1 - \beta _1^t} \right)}}$

(25)

${\rm{ }}S_{dw}^c = \frac{{{\rm{ }}{s_{dw}}}}{{\left( {1 - \beta _2^t} \right)}}$

(26)

${\rm{ }}S_{db}^c = \frac{{{\rm{ }}{s_{db}}}}{{\left( {1 - \beta _2^t} \right)}}$

(27)

加入偏差修正之后, 即可对权重和偏置进行更新, 公式如下:

$w = w - \alpha \frac{{\mathop v\nolimits_{dw}^c }}{{\sqrt {\mathop s\nolimits_{dw}^c } + \varepsilon }}$

(28)

$b = b - \alpha \frac{{\mathop v\nolimits_{db}^c }}{{\sqrt {\mathop s\nolimits_{db}^c } + \varepsilon }}$

(29)

其中, $\alpha $ 为学习速率, 在训练过程中可以通过微调学习速率来优化权重的更新速度, $\varepsilon $ 为超参数, 取值通常为10⁻⁸.

在智能电网稳定性预测算法中, CNN模型中的权重 $w$ 和偏置 $b$ 在一次次的迭代过程中不断被更新, CNN算法通过不断地迭代, 去更新权重 $w$ 和偏置 $b$ , 使得Loss函数无线逼近一个趋近于0的极小值, 同时Accuracy函数会不断增大, 表明模型的预测效果在不断地迭代中变得越来越好.

2 结果及分析

本文提出了一种基于CNN的智能电网稳定性预测算法, 采用了kaggle上来自国外某电力系统的数据, 该数据包含60000个样本, 它含有每个网络参与者的反应时间、每个网络参与者产生(正)或消耗(负)的标准功率、每个网络参与者的价格弹性系数等12个特征.

为评价基于CNN的智能电网稳定性预测模型的训练效果, 本节利用相同的数据集进行了Loss函数和Accuracy函数的仿真, 并对比了SVM、AdaBoost, 随机森林3种不同的算法, 如图3和图4所示.

从图3、图4可以看出, 本文提出的算法与SVM、AdaBoost, 随机森林相比, 有着较高的准确率. 图3表明, 随着数据量的增大, 算法的准确度不断提高, 并且CNN算法的准确度要远远高于其余3种算法; 图4表明, 损失函数随着数据量的增大而不断减小且逐渐趋于稳定, CNN算法的损失函数始终处于最低水平. 因此, 可以认为CNN算法可以更好地为智能电网的稳定性作出预测.

本文还比较了Adam^[23], RMSprop^[24]、SGD以及带有动量的SGD(MSGD)4种不同优化算法对于CNN模型训练的影响^[25], 如图5和图6所示.

从图5、图6可以看出, CNN模型的Accuracy值与训练集的数量成正相关, Loss的值与训练集的数量之间成负相关, 并且随着智能电网数据集的增加, 该模型的Loss值和Accuarcy值逐渐趋于平稳. 图5表明, 在相同的数据集下, MSGD算法的准确度>Adam>RMSprop>SGD, 且随着数据集的增大, SGD算法的准确度逐渐趋于稳定且始终大于其余3种算法.图6表明, 4种优化算法的损失函数都随着数据量的增大而减小并趋于稳定, 且MSGD算法的损失函数始终小于其他3种算法. 这表明了, 带有动量的SGD算法比RMSprop、Adam、SGD算法有更好的训练效果.

图7、图8表明, CNN模型的Loss值与迭代次数成负相关, Accuracy值与迭代次数成正相关. 从图7可以看出, 算法的准确度: MSGD>Adam>RMSprop>SGD, 并且随着迭代次数的增加, 准确度不断提高. 从图8可以看出, 随着迭代次数的增加, 四种优化算法的损失函数都逐渐下降, 且MSGD算法的损失函数始终低于其他3种算法. 这表明MSGD算法比SGD、RMSprop以及Adam有更低的误差损失, 用MSGD算法去优化CNN模型具有更好的效果.

综上可以看出, 与SVM、AdaBoost, 随机森林相比, CNN模型特可以更好地帮助我们去预测智能电网的稳定性, 这是因为CNN特有的参数共享和稀疏连接功能可以自动化处理高维特征; 对于CNN模型的优化方面来讲, Adam和RMSprop是仅次于MSGD的最优的两个算法, 这两种算法都能够自适应学习速率, 其中, RMSprop采用了递推的形式记录历史梯度平均作为动量, 缓和了参数变化的剧烈程度; Adam综合了Momentum和RMSprop, 既记录了历史梯度均值作为动量, 又考虑了历史梯度平方和实现各个参数学习率的自适应调整, 因此, 两种算法都具有较好的训练效果. SGD方法的训练效果最差, 这是由于SGD方法的更新方向完全依赖于当前的batch, 更新不稳定造成的, 而在引入动量后, 它的更新在一定程度上保留了之前的方向, 同时利用batch的梯度对当前方向进行微调, 这样一来, 可以学习得更快同时还有一定摆脱局部最优的能力, 因此, MSGD的训练效果很好并且超过了Adam和RMSprop算法.

3 结束语

本文提出了一个基于5G和CNN的智能电网稳定性预测算法, 首先对电力网络产生的数据进行采集, 接着针对采集到的数据进行预处理并输入进CNN模型, 经过CNN的卷积、池化、以及Softmax函数等的处理以及不断地迭代, 最终得到智能电网稳定性预测模型. 同时, 为了探究不同优化算法对于CNN预测模型的影响, 分别利用SGD、MSGD, RMSprop以及Adam对模型进行优化和训练, 对比了3种算法在不同情况下的Accuracy和Loss值变化情况. 最终的结果表明, 带有动量的SGD算法(MSGD)去优化CNN模型可以达到98.13%预测效果, 利用该模型可以有效地帮助电力系统对未知的问题提前预警, 降低了安全隐患, 避免了电力事故的发生.