随着我国社会经济的发展, 道路上的车辆数不断增加. 然而, 传统汽车过度依赖化石能源, 长远看, 不但会造成资源枯竭, 还会导致严重的环境污染. 电动汽车的出现较好地解决了上述问题. 电动汽车使用可再生的电能作为动力, 并且在使用过程中不产生尾气等污染物. 由于有着诸多优点, 电动汽车行业得到了国家的重点扶持, 近年来发展迅猛. 然而, 电动汽车有着充电时间长、续航短的特点, 并且当下城市充电设施不完善, 充电站分布不均衡, 直接导致电动汽车补充能源较燃油车困难, 已经成为其进一步推广发展的障碍. 解决电动汽车的续航问题较为直接的方式有两种: 一是提升电池容量; 二是大量建设充电桩并提升充电速度. 但当下电池技术短期内难以取得较大突破, 电池容量及充电速度提升潜力有限. 此外, 现代城市人口密集, 城市规划缺乏前瞻性, 改造成本高昂等原因导致充电桩、充电站难以大规模铺开建设. 在充电资源较为紧张的情况下, 我们发现公共充电桩的使用率依然较为低下. 据北京市发布的2018年10月的数据表明, 北京市公共充电桩的利用率仅为7%左右. 据一份欧洲的研究报告显示仅有5%的电动车辆长期使用公共充电桩^[1]. 美国爱荷华州国家实验室对5000余充电桩的使用情况进行统计. 结果表明交通便利的充电桩每周约有7次的充电行为, 与之对应的是位置偏僻的充电桩每周只有约1.4次的充电行为^[2], 大量的充电资源得不到有效利用.

随着车联网技术的发展^[3], 如何调度电动汽车合理充电, 成为近年来研究的热点. 通过研究电动汽车的历史出行数据, 对区域内的充电负荷进行预测, 可以对当前车辆的充电行为进行合理调度. 有学者提出基于空间负荷分布的车辆充电调度策略, 通过对行驶过程的动态分析, 结合电网负荷状态、交通数据, 可以将充电车辆匹配到合适的充电站^[4]. 有研究学者使用了马尔可夫决策过程和汽车随机出行链建立了车辆充电需求的时空模型, 得到了不同场景下的预测充电需求模型^[5]. 此外, 通过调节电价也可以有效的引导车辆充电行为, 该方法客观上能够避免单点充电负荷过高, 从而提高了充电站的使用率. 基于此有学者将蚁群算法与合理调整电价相结合, 提出了一种任务调度算法, 能够较好地降低用户成本和充电站负荷^[6]. Masoum等人提出了一种充电定价与优先级方案, 通过控制电动汽车的充电时段, 来缓解局部区域的供电压力^[7]. 还有部分学者从电网侧的供电安全出发^[8], 设计了电动汽车充电调度算法. Zhao等人提出的基于ZigBee和GPRS无线通信网络技术的电动汽车有序充电方法, 通过控制电动汽车的无序充电, 避免了电网和配电设施因过载而产生损耗^[9]. Aguado等人提出了一种混合整数线性规划策略, 用于调度电动车队与电网交换能量的行为, 避免自身的充电行为对当地电力系统产生影响^[10]. 上述研究多基于电网端的因素考量, 针对用户端的充电体验考量不足; 而针对用户端的研究多通过研究历史数据来对当前的充电需求进行预测, 使得调度缺乏实时性, 不能较好地应对突发情况.

实时路况作为一种重要的交通数据, 越来越为人们所重视^[11,12]. 为此, 本文提出一种基于实时路况的电动汽车充电调度算法. 本算法综合考虑实时路网内的道路拥堵情况以及充电站内的排队情况, 对充电车辆进行统一调度, 使车辆避开较为拥堵的路线, 并且选择距离较近, 充电排队车辆较少, 排队时间较短的充电桩进行充电服务, 以达到提高充电效率, 节约充电时间的目的. 仿真实验的数据表明: 本算法能够较好地解决车辆充电的盲目性以及区域内充电站负载不均衡的问题.

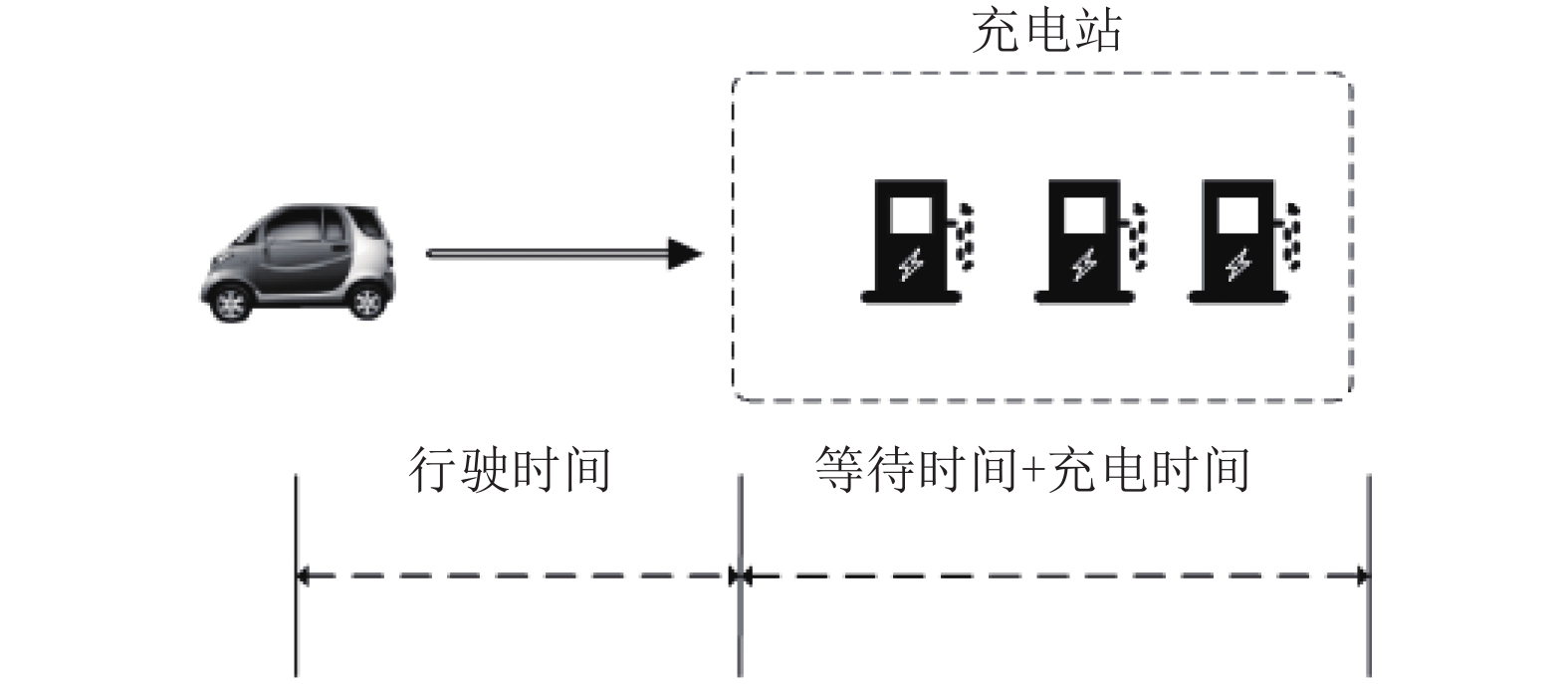
1 电动汽车充电耗时分析 1.1 耗时分析

电动汽车充电的耗时过程如图1所示, 充电所消耗时间包括: 电动汽车到达充电站的行驶时间、在充电站的排队等待时间、将电池充满所需要充电时间.

1)路程

充电路程是指电动汽车从当前位置到充电桩所经过的道路里程总和. 为了量化电动汽车到充电桩经过的道路里程, 本文假设待充电车辆从起点到充电桩的路径是按照最短路径行驶, 最短路径采用迪杰斯特拉算法^[13](以下简称最短路径算法)计算得到.

根据最短路径算法, 将电动汽车i到充电桩j的最短路径所途径的路段分别记为 ${d_{ij1}}$ , ${d_{ij{\rm{2}}}}$ , ${d_{ij{\rm{3}}}}$ 电动汽车行驶的总路程 ${d_{ij}}$ 可用式(1)表示:

${d_{ij}} = {d_{ij1}} + {d_{ij2}} + {d_{ij3}} + \cdots +{d_{ijn}}$

(1)

2)时间

电动汽车充电所消耗的时间包括: 从当前位置到充电站的行驶时间、充电站内的排队时间、充电时间, 即:

${{{T}}_{\rm {total}}} = {a_{ij}} + {t_w} + {t_c}$

(2)

其中, ${{{T}}_{\rm {total}}}$ 表示电动汽车充电花费的各项时间之和; ${a_{ij}}$ 表示车辆 $i$ 到达充电桩j通过各路段所消耗的时间; ${t_w}$ 表示排队时间; ${t_c}$ 表示充电时间.

行驶时间 ${a_{ij}}$ :

${a_{ij}} = \frac{{{d_{ij1}}}}{{{v_{ij1}}}} + \frac{{{d_{ij2}}}}{{{v_{ij2}}}} + \cdots + \frac{{{d_{ijn}}}}{{{v_{ijn}}}}$

(3)

其中, ${a_{ij}}$ 表示车辆 $i$ 到达充电桩j通过各路段所消耗的时间和; ${d_{ij1}},{d_{ij2}}, \cdots ,{d_{ijn}}$ 表示车辆 $i$ 到达充电桩j充电, 所经过的各路段的长度; ${v_{ij1}},{v_{ij2}}, \cdots ,{v_{ijn}}$ 表示车辆 $i$ 到达充电桩j充电, 所经过的各路段的速度.

排队时间 ${t_w}$ : 表示车辆抵达充电站后, 若有前车排队, 则需等待前车完成充电服务后, 再进行充电, 等待时间即为排队时间; 若无前车, 则无需等待, 即排队时间为0.

充电时间 ${t_c}$ : 表示待充电车辆排队结束, 开始充电到充电完成所消耗的时间. 充电时长可由式(4)计算出.

$ {t_{ic}} = \frac{{s_{\rm {vol}}^i - \left( {s_{\rm {ini}}^i - s_{\rm {con}}^i} \right)}}{{{V_{in}}}} $

(4)

其中, ${t_{ic}}$ 表示车辆i的充电时间; $s_{\rm {vol}}^i$ 表示车辆i的电池容量; $s_{\rm {ini}}^i$ 表示车辆i的初始电量; $s_{_{\rm {con}}}^i$ 表示车辆i从起点到充电桩消耗的电能; $V_{in}^{}$ 表示车辆i的充电功率.

1.2 相关说明

1)本文从地图商网站抓取西安市城区某时段的道路交通数据^[14], 其中包含: 道路编码、道路名称、道路等级、道路方向、起始路段、终止路段、平均速度等^[15].

2)在未调度的情况下, 我们认为电动汽车从起点到充电站是按照最短距离行驶的, 本文使用最短路径算法模拟未调度的情况.

3)所有车辆的电池容量相同, 电量随着行驶时间线性消耗.

4)充电站设备全部正常, 每个充电桩每次服务一辆汽车.

5)每辆电动汽车的剩余续驶里程, 至少可以到达一个充电站.

6)电动汽车及充电桩分布在路网中, 调度时按照就近原则将其归纳到就近的路口. 调度过程简化为从路口到路口的调度.

7)电动车辆和充电桩的接口是兼容的.

8)某一时刻发起充电请求的车辆数目为一定值, 且通信时延忽略不计^[16].

2 调度算法 2.1 算法描述

电动汽车在前往充电的时候往往会考虑两个方面的因素, 一是距离充电站的距离; 二是到达目标充电站的路况. 若选择较近的充电站进行充电, 站内可能需要较长时间的排队; 若选择较为空闲的充电站, 则可能路途较远, 交通情况较为拥堵, 花费更多的时间.

针对上述的选择问题, 我们在综合考虑交通路网拥堵情况、各充电站内的排队情况、距离充电站的路程等因素后, 提出了一种以节约不必要的充电时间开销为目的, 以提升全局充电效率为导向的基于实时路况的电动汽车充电调度算法. 该算法说明如下.

根据建立的道路交通路网模型以及电动汽车充电行为分析结果, 我们在选定的路网范围内, 由最短路径算法可求得电动汽车到每个充电桩的最短距离. 路网内的充电桩及电动车辆均与服务器互联, 实时共享自身的位置信息、充电状态等信息.

某时刻路网内的待充电的电动汽车I, 共n个, 用 $E{V_i}$ 表示:

$I = \{ 1,2,3, \cdots, n\} $

路网内的充电站Y, 用 $C{S_y}$ 表示:

$Y = \{ 1,2,3, \cdots, y\} $

其中, 每个充电站 $C{S_y}$ 内有k个充电桩 $j{}_{yx},x = 1,2,3, \cdots, k$ , 故区域内共有m个充电桩:

$\mathop \sum \limits_{i = 0}^y \mathop \sum \limits_{x = 1}^k {j_{ix}} = m$

该m个充电桩统一编号为:

${j_{y1}}{j_{y2}}{j_{y3}} \cdots {j_{ym}}(y \in {{Y}})$

其中, ${d_{iy}}$ 表示电动汽车 $E{V_i}$ 到充电站 $C{S_y}$ 的距离, ${d_{i{j_{yx}}}}$ 表示电动汽车到该充电站内某个充电桩的距离; 我们认为: 在不影响计算结果的前提下, 电动汽车 $E{V_i}$ 到充电站 $C{S_y}$ 的距离和到该站内充电桩的距离可以认为是近似相等的, 故有:

${d_{iy}} = {d_{i{j_{yx}}}}({\rm{y}} \in Y,x = 1,2,3, \cdots, k)$

在电动汽车可达范围内, 对于任意电动汽车 $E{V_i}$ 到任意充电桩 $j{}_{yx}$ 的距离 ${d_{i{j_{yx}}}}$ 都是确定的, 按式(3)计算出电动汽车 $E{V_i}$ 到充电桩 ${d_{i{j_{yx}}}}$ 的时间.

某一时刻, 充电桩 ${j_{yx}}$ 经过 $t_{yx}^{}$ 时长后, 切换到空闲状态.

2.2 算法步骤

结合上述内容, 下面给出基于实时路况的电动汽车充电调度算法, 步骤如下:

Step 1. 某一时刻, 服务器接收到相关车辆发起的充电请求, 并获得该时刻各充电桩切换到空闲状态所消耗的时长 $t_{yx}^{}$ ;

Step 2. 根据发起请求的顺序对车辆进行编号, 首先对车辆 $E{V_i}$ $(i = 1)$ 进行调度;

Step 3. 通过最短路径算法, 计算车辆 $E{V_i}$ 到各个充电桩的里程距离 ${d_{i{j_{yx}}}}$ , 并根据剩余电量确定车辆可抵达的充电桩. 对在续航范围内的充电桩 ${j_{yx}}$ , 进行时间开销计算;

Step 4. 车 $E{V_i}$ 完成充电所花费的总时长为 ${{{T}}_{\rm {total}}}$ , 充电桩 ${j_{yx}}$ 由忙碌切换到空闲状态的时长为 ${t_{yx}}$ , 由式(3)计算出车 $E{V_i}$ 到充电桩 ${j_{yx}}$ 的行驶时间 ${a_{i{j_{yx}}}}$ , 由式(4)计算出车辆充电时间为 ${t_c}$ ;

Step 5. 若 ${a_{i{j_{yx}}}}$ > ${t_{yx}}$ ,说明充电无需排队, 车 $E{V_i}$ 到该桩充电花费总时长 ${{{T}}_{\rm {total}}} = {t_c} + {a_{i{j_{yx}}}}$ ;

Step 6. 若 ${a_{i{j_{yx}}}}$ < ${t_{yx}}$ ,说明充电需要排队, 车 $E{V_i}$ 到该桩充电花费总时长 ${{{T}}_{\rm {total}}} = {t_c} + {t_{yx}}$ ;

Step 7. 在车辆 $E{V_i}$ 续航可达的充电桩中, 选择 ${{{T}}_{\rm {total}}}$ 最小的充电桩进行调度, 即能最快完成充电服务的充电桩, 完成车辆 $E{V_i}$ 的调度;

Step 8. 若车 $E{V_i}$ 为本次调度的最后一辆车, 则结束本次调度; 否则令 $i = i + 1$ , 转到Step 3.

3 实验及结果分析 3.1 实验数据

使用爬虫工具抓取实时道路数据后, 存入数据库中待用. 实时道路数据如表1所示.

此外, 根据实际数据构建的路网图包括以下内容: 17个充电站(共计222个充电桩)、90个节点、309条路段. 各节点的充电桩分布如表2所示.

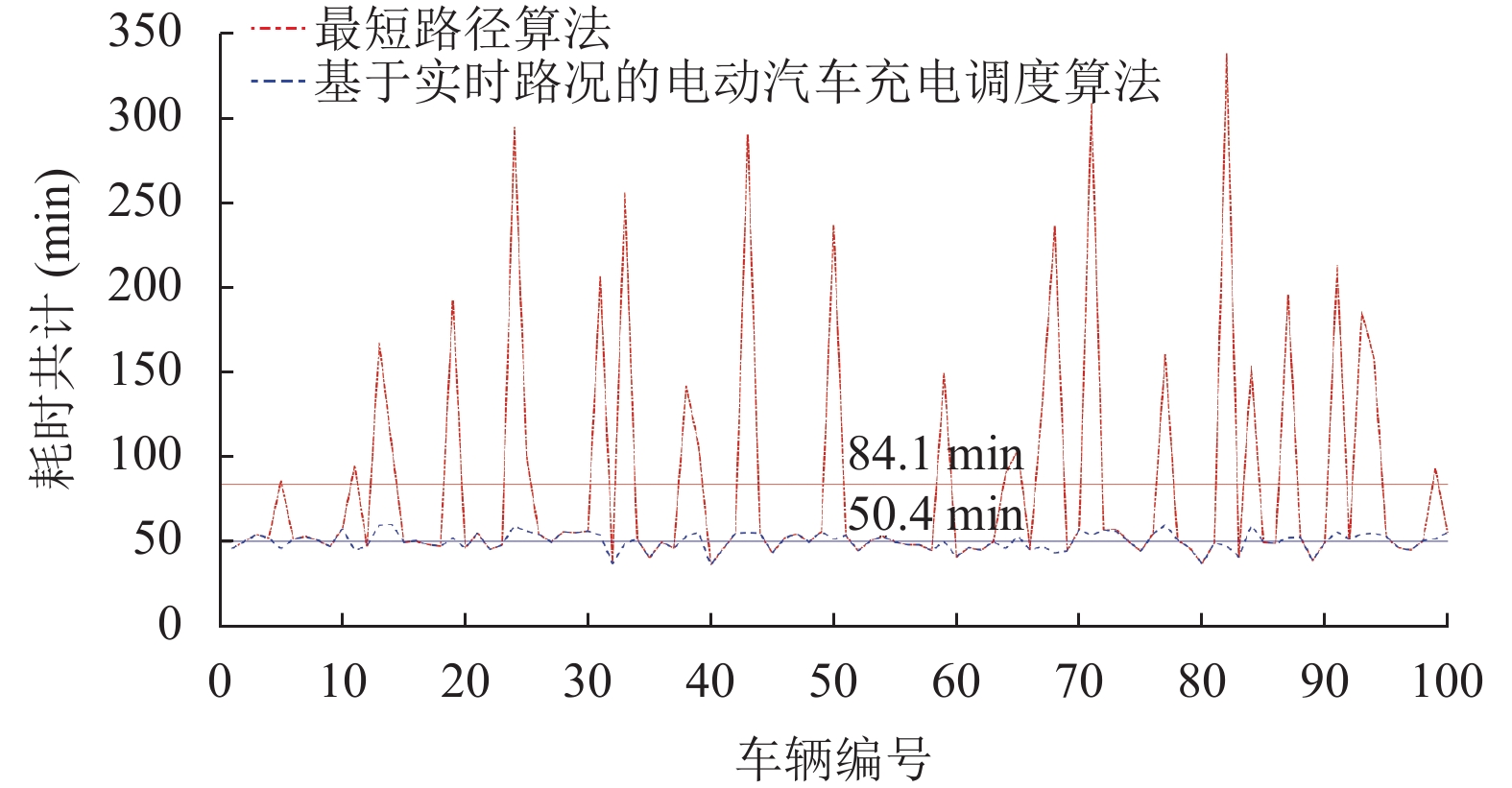
3.2 仿真结果

在路网内的各个节点处, 模拟生成100辆待充电的电动汽车(剩余电量为总电量的20%–40%不等). 对路网中随机生成的电动汽车进行调度, 并与最短路径算法下(即未调度情况)的结果进行了对比, 仿真结果如图2所示.

由图2可知, 基于最短路径算法下的100辆电动汽车的平均充电时间为84.1分钟, 而基于实时路况的电动汽车充电调度算法的平均充电时间为50.4分钟. 图2中一些折线重合, 表明在两种算法下该编号的车都调度到同一个充电桩进行充电服务.

根据调度结果可知, 在同时间段的交通路况下对有充电需求的车辆使用本算法进行调度, 能够明显降低全局车辆的平均充电时间.

两种调度算法下, 各充电站服务车辆的具体数据如表3所示.

我们使用参数 $\;{\rho _y}$ 来描述各个充电站 $C{S_y}$ 的负载:

$ {\rho _y} = \frac{{{n_y}}}{{{J_{{y}}}}} $

(5)

其中, ${n_y}$ 表示充电站内实际服务的电动汽车数量; ${J_y}$ 表示充电站内充电桩的数量.

如果进行充电的电动汽车分布越均衡, 那么各充电站的负载值越接近, 充电站负载值的方差越小, 计算Y个充电站负载值的方差如式(6)所示:

$ {S_\rho }^{\rm{2}} = \frac{1}{Y}{\sum\limits_{y = 1}^Y {\left( {{\rho _y} - \frac{1}{Y}\sum\limits_{y = 1}^Y {{\rho _y}} } \right)} ^{\rm{2}}} $

(6)

由表3及式(6), 可以计算出两种调度算法的方差, 结果如表4所示.

由表4可知, 通过本算法对车辆进行调度, 能够有效平衡各个充电站的负载情况, 即各充电站的充电资源可以得到有效的利用.

4 总结与展望

本文基于电动汽车的充电特点与需求, 建立了电动汽车充电问题的数学模型. 以提升电动汽车用户体验, 优化路网内电动汽车总体充电效率为导向提出了调度算法, 并进行了仿真实验.

本算法采用了实时交通数据作为调度依据, 使调度策略更符合实际交通状况, 避免了采用历史数据对当前路况进行预测的不准确性, 提高了调度效率. 此外, 本算法将道路拥挤程度, 充电站内排队状况纳入考虑, 使调度更为准确、高效, 避免了通过单一计算路程来确定目的充电站的不可靠性. 总的来说, 本算法通过全局调度, 既降低了车辆的平均充电时间, 又使区域内的充电站负载更加均衡, 提高了充电站的利用率. 本算法的不足之处在于, 算法运行的部分条件较为理想, 接下来的研究可以将现实中的各类细节及不确定因素添加到算法中来, 使其调度更加精准; 此外, 也可针对调度过程进行优化, 来获得更高的调度效率.