基于编解码网络的人脸对齐和重建算法

引用本文

曾远强, 蔡坚勇, 章小曼, 卢依宏. 基于编解码网络的人脸对齐和重建算法. 计算机系统应用, 2021, 30(7): 184-189.http://www.c-s-a.org.cn/1003-3254/8011.html

Zeng YQ, Cai JY, Zhang XM, Lu YH. Face Alignment and Reconstruction Based on Encoder-Decoder Network. Computer Systems and Applications, 2021, 30(7): 184-189(in Chinese).http://www.c-s-a.org.cn/1003-3254/8011.html

基于编解码网络的人脸对齐和重建算法

曾远强¹, 蔡坚勇^1,2,3,4, 章小曼¹, 卢依宏¹

1. 福建师范大学光电与信息工程学院, 福州 350007;
2. 福建师范大学医学光电科学与技术教育部重点实验室, 福州 350007;
3. 福建师范大学福建省光子技术重点实验室, 福州 350007;
4. 福建师范大学福建省光电传感应用工程技术研究中心, 福州 350007

收稿日期：2020-11-04; 修改日期：2020-12-02; 采用时间：2020-12-25; csa 在线出版时间：2021-06-30

基金项目：福建省教育厅资助项目(JAT170128)

通讯作者：蔡坚勇, E-mail: cjy@fjnu.edu.cn.

摘要：针对现有的三维人脸重建模型复杂度较高和对多种人脸姿态重建效果不佳的问题, 本文提出了一种可以在不同人脸姿态条件下, 有效地实现人脸对齐并从单张二维人脸图片重建出三维人脸的卷积神经网络. 首先设计了由密集卷积网络模块和转置卷积模块构成的编解码网络, 并在损失函数中引入图像结构相似度评价, 构造新的损失函数, 通过训练神经网络得出模型, 模型实现了人脸对齐和三维人脸重建任务. 在AFLW2000-3D数据集上验证性能, 实验表明该网络有效提升了人脸对齐和人脸重建的效果.

关键词: 编解码网络密集卷积网络损失函数三维人脸重建人脸对齐

Face Alignment and Reconstruction Based on Encoder-Decoder Network

ZENG Yuan-Qiang¹, CAI Jian-Yong^1,2,3,4, ZHANG Xiao-Man¹, LU Yi-Hong¹

1. College of Photonic and Electronic Engineering, Fujian Normal University, Fuzhou 350007, China;
2. Key Laboratory of Optoelectronic Science and Technology for Medicine of Ministry of Education, Fujian Normal University, Fuzhou 350007, China;
3. Fujian Provincial Key Laboratory of Photonics Technology, Fujian Normal University, Fuzhou 350007, China;
4. Fujian Provincial Engineering Technology Research Center of Photoelectric Sensing Application, Fujian Normal University, Fuzhou 350007, China

Foundation item: Fund of Education Bureau, Fujian Province (JAT170128)

Abstract: The existing 3D face reconstruction models have the problems of high complexity and poor reconstruction accuracy of multiple face poses. For these reasons, we propose a convolutional neural network that can effectively achieve face alignment and reconstruct a 3D face from a single face picture in the case of a variety of face poses. First, we design an encoder-decoder network composed of a DenseNet module and a deconvolution module. The evaluation of image Structural SIMilarity (SSIM) is introduced into the loss function to construct a new loss function. Then, we train the neural network to get a model, which implements face alignment and 3D face reconstruction tasks. Experiments on the ALFW2000-3D dataset show that the proposed network effectively improves the accuracy of face alignment and reconstruction.

Key words: encoder-decoder network DenseNet loss function 3D face reconstruction face alignment

1 引言

人脸对齐和三维人脸重建是计算机视觉领域中两个相关联且具有挑战性的课题, 在信息安全, 智慧城市, 影视娱乐等领域有着广泛的应用. 其中信息安全领域对人脸重建模型的计算速度和质量都有较高的要求. 例如在人脸识别的应用中, 二维人脸识别在大姿态人脸的条件下识别效果较差, 而三维人脸因为包含更丰富的人脸信息, 可以较好的克服人脸姿态的影响. 三维人脸识别系统一般需要经过人脸对齐的步骤, 然后利用三维人脸重建模型从二维人脸图片中重建出三维人脸用于人脸识别, 其中的人脸对齐和人脸重建是其中两个重要的步骤. 人脸对齐的精度, 人脸重建的质量和模型的运行速度是其中的关键因素, 本文将在已有研究的基础上创新改进三维人脸重建模型, 提高模型的性能.

二维人脸对齐的研究工作主要是为了实现人脸关键点的定位, 并用于人脸识别或者辅助人脸重建等任务. 早期比较具有代表性的工作如主观形状模型(ASM)^[1], 作者首先用人脸样本构建出一个平均人脸, 然后用68个已标定的人脸关键点描述模型对齐的人脸, 通过迭代搜索对应特征点, 不断优化参数, 直至搜索的特征点和对应标定的特征点最为接近. 该方法实现的人脸对齐效果精度较低, 且容易受到图像噪声影响. 一些工作^{[2, 3]}基于主观形状模型进行优化, 得到了改进, 但是精确度仍然较差. 随着深度学习的发展, 目前通过二维人脸图片进行人脸对齐取得较好效果的是基于卷积神经网络(CNN)的方法^[4], 但是这类方法只能描述图片中人脸的可见区域, 其性能会在面部遮挡、头部姿态等外界因素的干扰下受到影响. 与二维人脸相比, 三维人脸在空间中保留了更多的信息, 不受人脸姿态等因素的影响. 一些研究在Blanz等人^[5]提出的三维人脸形变模型3DMM的基础上, 通过拟合3DMM参数去实现三维人脸对齐, 在精准性和鲁棒性方面都有所提升. 如Zhu等人^[6]提出的3DDFA, 作者将PNCC和PAF做为输入特征, 设计了一个级联卷积神经网络作为回归因子计算模型参数, 将3DMM拟合到二维图像, 实现了人脸关键点定位和人脸密集对齐, 性能优于基于二维人脸图片的对齐方式. 通过拟合3DMM参数实现人脸对齐的方法由于人脸模型中间参数的影响, 模型性能受到限制. 近来, Yao等人^[7]提出的PRN, 采用UV位置图表示三维人脸, 以端到端的训练方式克服了中间参数的影响, 使模型在运行速度和人脸对齐效果上都得到了提升. 但是受其网络架构的影响, 其模型冗余度和对齐的精确度仍然有待改进.

在人脸重建方面, 传统的三维人脸重建方法主要基于3DMM模型实现, 早期的方法^{[8, 9]}通过建立二维图像与3DMM模型的特征点之间的对应关系, 求解优化函数回归3DMM参数, 这类方法受初始特征点检测精度的影响较大, 且重建过程复杂. 在卷积神经网络发展的影响下, 一些方法^{[10, 11]}使用CNN直接学习3DMM的参数, 相比于传统算法在重建质量和速度上都有所提升. 然而, 基于固有模型重建的方法因为受到模型几何空间的限制, 所实现的重建效果也不理想.

为了克服上述研究的缺陷, 近来有一些研究提出采用端到端的方式实现三维人脸齐重建, 摆脱了固有参数模型的空间限制, 实现了较好的人脸重建效果. VRN^[12]采用体素表示三维人脸, 设计了由多个沙漏模块构成的卷积神经网络进行回归训练, 相比上述方法取得了更好的效果, 但是文中采用了体素的表示方式表示三维人脸, 丢弃了点的语义信息, 为了从单张二维人脸图片重建出完整的三维人脸形状, 需要复杂的网络对整个体积进行回归, 增加了计算的复杂度. PRN^[7]采用了UV位置图的方式表示三维人脸, 有效保留了点的语义信息. 并设计一个由残差模块和转置卷积模块构成的编解码网络, 结合文中所提的权重损失函数进行训练, 取得了更好的性能. 其中编码网络主要采用如图1所示的残差模块^[13]构成, 方框中的参数为卷积核的大小, 设输入的特征图为x, 则残差模块的输出H(x)可表示为式(1). 残差模块通过跳接的方法, 克服深层网络中的梯度消失问题, 加强了模型的特征提取能力. 但是由于PRN构建的编码网络层数较深, 参数数量达到 $9.43 \times {10^5}$ 个, 模型的冗余度仍有待进一步优化, 另一方面在其损失函数限制下, 其模型的对齐和重建质量也有待提升.

$H(x)=F(x) + x$

(1)

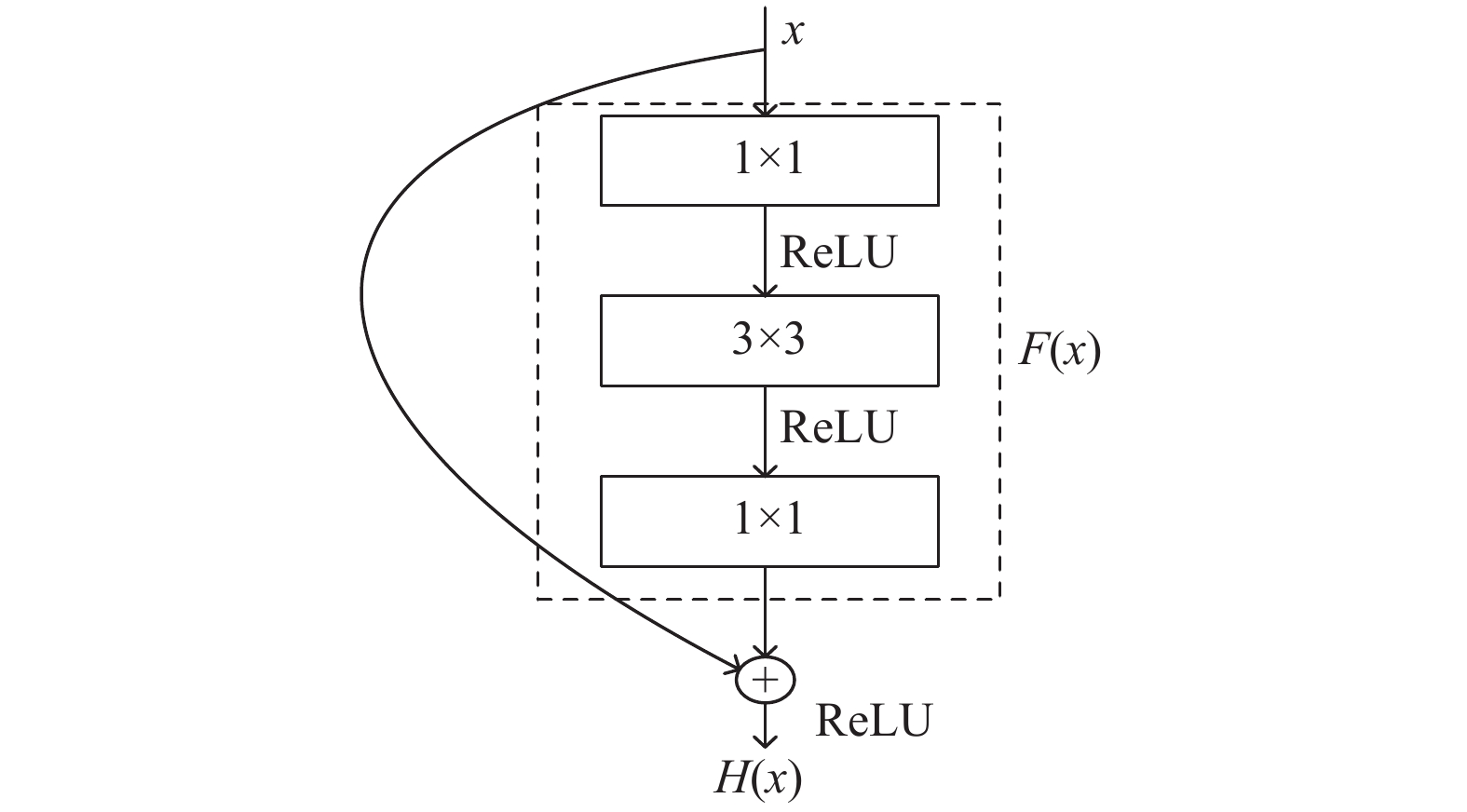
图 1 残差模块示意图

本文所提的方法是在PRN工作基础上的创新改进, 有效提高了三维人脸对齐和重建的质量, 本文主要工作如下:

(1)设计了一个全新的由密集卷积模块和转置卷积模块构成的编解码网络, 经过实际运算得出, 相比PRN网络的参数数量减少了 $1.76 \times {10^5}$ 个, 有效降低了模型的冗余度, 提高模型运算速度.

(2)在损失函数中引入图像结构相似度, 借鉴PRN的权重损失函数思想, 提高了三维人脸对齐和重建质量.

(3)在AFLW2000-3D数据集^[6]上验证效果并与其他方法作出对比, 实验表明本文的方法在人脸重建和人脸对齐方面都取得了较好的效果.

2 方法

这个部分将论述网络架构的实现和损失函数的设计. 本文所提出的网络架构包括两部分:

(1)基于密集卷积模块构成的编码网络;

(2)基于转置卷积模块构成的解码网络.

2.1 基于密集卷积模块的编码网络

本文采用密集卷积模块的架构去设计编码网络. 密集卷积模块来源于^[14]提出的密集卷积网络(DenseNet), 如图2所示, 其中方框表示卷积层, 作者用前反馈的方式将网络中的每一层拼接到之后的每一层网络中, 不同于PRN用残差模块的跳接求和方式, 密集卷积模块将前面所有层的特征图拼接用作当前层的输入, 即第l层可以接收到前l–1层的所有特征图作为输入, 如图2的连接状态可表示为式(1), 其中 $[{x_0},{x_1}, {x_2},{x_3}]$ 表示前面各层特征图的拼接, H函数表示当前层的权重运算. DenseNet架构通过密集连接和特征复用, 可以缓解梯度消失问题, 并减少参数的数量, 性能优于残差卷积网络.

$ {X_4}={H_4}([{x_0},{x_1},{x_2},{x_3}]) $

(2)

图 2 密集卷积模块示意图

本文的编码网络主要由6个密集卷积模块构成. 首先第一层是3×3的卷积层用于提取输入图片的特征, 接下去则是密集卷积模块和过渡层组成的网络. 每个密集卷积模块包含批量归一化层BN (Batch Normalization), 1×1卷积层和3×3卷积层共3个小模块. 过渡层由一个批量归一化层连接一个1×1的卷积层和2×2的平均池化层组成. 1×1的卷积层的设定是为了控制输入特征图的通道数量, 提高网络的运算效率, 使用平均池化层则是因为其在保留图片的局部信息相对其他池化方式有优势, 适合我们的人脸重建任务. 网络架构示意图如图3, 网络各层参数及特征图维度变换如表1所示. 本文将图片的维度表示为H×W×B, 其中H和W分别表示图片的高和宽, B表示图片的通道数. 该编码网络可以将维度为256×256×3的输入图片转换为8×8×512的特征图.

图 3 编码网络架构示意图

2.2 基于反卷积模块的解码网络

我们在编码网络中将特征图的维度缩小后, 需要用转置卷积构成的解码网络进行上采样, 预测出维度为256×256×3的位置图. 该编码网络采用两种转置卷积, 一种用于上采样, 卷积核的大小为4×4, 步长为2. 零填充padding为1, 一种用于维持形状, 对特征图进行整理, 其卷积核大小为3×3, 步长为1, 零填充padding为1.

设反卷积输入的特征图维度为i, 输出的特征图维度为o, 卷积核大小为k, 步长为s, 零填充个数为p, 转置卷积对特征图的维度转换公式如式(3)所示:

$o=s(i - 1) + k - 2p$

(3)

图4中第1层卷积的输出图片的维度应为 $o={\rm{1}} \times $ $ (i - 1) + {\rm{3 - 2}}=i$ , 即特征图维度不变. 第2层转置卷积的维度为 $o={\rm{2}} \times (i - 1) + {\rm{4 - 2}}={\rm{2}}i$ , 实现了对特征图的上采样. 第3层转置卷积同第1层.

解码网络的每一个模块由如图4所示3个小模块构成. 最后我们设计了一个由5个该模块构成的解码网络, 将编码网络输出的维度8×8×512的特征图上采样为256×256×3, 输出预测的结果.

2.3 损失函数

在PRN中作者提出了权重损失函数的方法, 通过设置权重矩阵, 将训练的重点集中在人脸关键的区域, 忽略脸部以外部分, 提高了训练的效率. 该权重矩阵W设置的比例为: (人脸68个关键点):(眼嘴鼻):(人脸其他区域):(人脸以外区域)=16:4:3:0, 其各区域划分可参考图5. 本文借鉴权重损失函数这一方法, 考虑真实图片与预测后图片的结构相在损失函数中引入图像结构相似度SSIM^[15]创建了一个新的损失函数. SSIM可结合亮度, 对比度和结构3方面因素比较两张图片, 假设输入的两张图像分别为x和y, 定义SSIM为式(4).

$SSIM(x, y)={[l(x, y)]^\alpha }{[c(x, y)]^\beta }{[s(x, y)]^\gamma }$

(4)

其中, l(x, y)表示亮度比较函数, c(x,y)表示对比度比较函数, s(x, y)表示结构比较函数. 设x的平均值 $\;{\mu _x}=\dfrac{{\rm{1}}}{N}\displaystyle\sum\limits_{{\rm{i}}=1}^N {{x_i}}$ , 标准差为 ${\sigma _x} = {\left( {\dfrac{1}{{N - 1}}\displaystyle\sum\limits_{i = 1}^N {({x_i} - {\mu _x}} {)^2}} \right)^{\textstyle\frac{1}{2}}}$ , y的平均值 ${\mu _{\rm{y}}}$ 和标准差 ${\sigma _{\rm{y}}}$ 计算同x. 图像x和y的协方差表示为 ${\sigma _{xy}}=\dfrac{1}{{N - 1}}\displaystyle\sum\limits_{{\rm{i}}={\rm{1}}}^N {({x_i} - {\mu _x})({y_i} - {\mu _y})} $ .

表 1 编码网络输出特征图大小各层参数

模块	输出维度	层
Conv1	${\rm{256}} \times {\rm{256}} \times {\rm{16}}$	${\rm{3}} \times {\rm{3Conv}}$
Dense Block(1)	${\rm{256}} \times {\rm{256}} \times {\rm{96}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv} } } \end{array} } \right\} \times 3$
Transition Layer(1)	${\rm{256}} \times {\rm{256}} \times {\rm{48}}$	${\rm{1} } \times {\rm{1} }{\rm {Conv}}$
Transition Layer(1)	$128 \times 128 \times {\rm{48}}$	${\rm{2} } \times {{2} }{\rm {average\_pool}}$ , stride=2
Dense Block(2)	$128 \times 128 \times {\rm{200}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv}}} \end{array} } \right\} \times 3$
Transition Layer(2)	$128 \times 128 \times {\rm{104}}$	${\rm{1} } \times {\rm{1} }{\rm {Conv}}$
Transition Layer(2)	${\rm{64}} \times {\rm{64}} \times {\rm{104}}$	${\rm{2} } \times {\rm{2} }{\rm {average\_pool}}$ , stride=2
Dense Block(3)	${\rm{64}} \times {\rm{64}} \times {\rm{256}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv}}} \end{array} } \right\} \times 3$
Transition Layer(3)	${\rm{64}} \times {\rm{64}} \times {\rm{160}}$	${\rm{1}} \times {\rm{1}}Conv$
Transition Layer(3)	${\rm{32}} \times {\rm{32}} \times {\rm{160}}$	${\rm{2} } \times {\rm{2} }{\rm {average\_pool}}$ , stride=2
Dense Block(4)	${\rm{32}} \times {\rm{32}} \times {\rm{328}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv}}} \end{array} } \right\} \times 3$
Transition Layer(4)	${\rm{32}} \times {\rm{32}} \times {\rm{232}}$	${\rm{1}} \times {\rm{1}}Conv$
Transition Layer(4)	${\rm{16}} \times {\rm{16}} \times {\rm{232}}$	${\rm{2} } \times {\rm{2} }{\rm {average\_pool}}$ , stride=2
Dense Block(5)	${\rm{16}} \times {\rm{16}} \times {\rm{528}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv}}} \end{array} } \right\} \times 3$
Transition Layer(5)	${\rm{16}} \times {\rm{16}} \times {\rm{528}}$	${\rm{1} } \times {\rm{1} }{\rm {Conv}}$
Transition Layer(5)	${\rm{8}} \times {\rm{8}} \times {\rm{336}}$	${\rm{2} } \times {\rm{2} }{\rm {average\_pool}}$ , stride=2
Dense Block(6)	${\rm{8}} \times {\rm{8}} \times {\rm{512}}$	$\left\{ {\begin{array}{*{20}{c} } {1 \times 1{\rm {Conv}}} \\ {3 \times 3{\rm {Conv}}} \end{array} } \right\} \times 3$

表 1 编码网络输出特征图大小各层参数

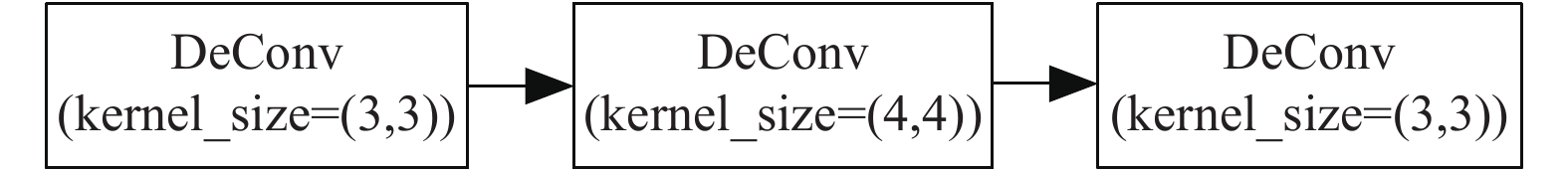
图 4 转置卷积模块示意图

l(x, y), c(x, y)和s(x, y)分别定义如下:

$l(x, y)=\frac{{2{\mu _x}{\mu _y} + {C_1}}}{{\mu _x^2 + \mu _y^2 + {C_1}}}$

(5)

$c(x, y)=\frac{{2{\sigma _{xy}} + {C_2}}}{{\sigma _x^2 + \sigma _y^2 + {C_2}}}$

(6)

$s(x, y)=\frac{{{\sigma _{xy}} + {C_3}}}{{{\sigma _x}{\sigma _y} + {C_3}}}$

(7)

其中, ${C_1}$ 、 ${C_2}$ 、 ${C_3}$ 为常数, 避免分母接近于0时造成运算的不稳定. 这里取 ${C_3}=\dfrac{{{C_2}}}{2}$ , $\alpha =\beta =\gamma =1$ , 则SSIM可表示如下:

$SSIM = \frac{{(2{\mu _x}{\mu _y} + {C_1})(2{\sigma _{xy}} + {C_2})}}{{\left( {\mu _x^2 + \mu _y^2 + {C_1}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {C_2}} \right)}}$

(8)

结合人脸权重W, 定义损失函数Loss为:

$Loss=1 - SSIM(\bar y,y) \cdot W(\bar y,y)$

(9)

其中, ${\bar{{y}}}$ 和y分别代表网络输出的值和真实值, W(x, y)为权重矩阵. 在模型训练中, 令 ${C_1}$ =0.026, ${C_2}$ =0.058.

图 5 人脸权重矩阵各区域划分示意图

3 实验

这部分内容将介绍具体的训练过程, 并进行实验结果分析. 因为本文的模型能实现人脸对齐和人脸重建两部分的任务, 所以在我们的论述中将分别对这两项任务的实验数据与其他方法做出对比, 并通过效果图展示模型的效果.

3.1 训练过程 3.1.1 训练集

本文的目标是通过神经网络从单张二维人脸图片中回归出人脸对齐信息和三维人脸几何信息, 所以使用的训练集既要能让网络直接回归预测, 还应包含人脸对齐和三维人脸信息. 针对以上问题, 我们采用Yao等人在PRN^[7]中提出的将三维人脸转换为UV位置图的方式创建训练集. UV位置图是一种能在UV空间记录三维信息的二维图像^[16], Yao等人使用UV空间存储三维人脸模型中点的位置, 并在直角坐标系中将三维人脸模型的投影与相应的二维人脸图像对齐. 位置图Pos可以表示为:

$Pos({u_i},{v_i})=({x_i},{y_i},{{\textit{z}}_i})$

(10)

其中, $({u_i},{v_i})$ 表示UV空间中的第i个点, 与3维空间中的第i个点 $({x_i},{y_i},{{\textit{z}}_i})$ 对应, $({x_i},{y_i})$ 为对应二维图像的第i个点, ${{\textit{z}}_i}$ 表示该点的深度. $({u_i},{v_i})$ 和 $({x_i},{y_i})$ 表示相同的位置, 因此能够保留对齐的信息.

本文使用300W-LP数据集^[6]的部分数据作为训练集, 300W-LP包含各种无约束的二维人脸图片及其对应的三维人脸信息, 其中标注的信息包含人脸姿态参数, 68个人脸关键点等. 我们选取300W-LP中的AFW, HELEN及其对应的翻转图片, 并对其中部分图片进行平移旋转, 总共得到12万组数据作为训练集, 然后采用PRN^[7]所提方法在已有标注数据的基础上将其中的三维人脸信息转换到UV空间得到UV位置图, 构建出完整的训练集.

3.1.2 实验参数及环境

网络架构如第2节论述. 训练中设置批量大小为16, 使用Adam优化器, 根据训练的效果, 依次调整初始学习率为 $1 \times {10^{ - 4}}$ , $1 \times {10^{ - 6}}$ , $1 \times {10^{ - 8}}$ , 其他参数不变, 每个周期迭代7529次, 总共训练80个周期. 使用编程语言Python 3.6, 深度学习框架PyTorch 1.1.0, 在NVIDIA 1080ti GPU上完成训练, 每个完整的训练需3天时间.

3.2 实验分析 3.2.1 人脸对齐实验结果分析

首先是人脸对齐结果的分析. 我们使用的测试集是AFLW-3D数据集, 该数据集包含各种姿态的人脸参数以及68个人脸关键点参数, 被广泛用于人脸对齐的测试评估中. 经过训练得出模型, 对各种姿态的人脸对齐效果如图6所示, 第1行为各种姿态的人脸图片, 第2行为对齐的效果图.

根据AFLW-3D中偏航角(yaw)参数, 分类出[0, 30), [30, 60), [60, 90]三种不同头部姿态的部分图片进行对比实验. 采用归一化平均误差NME (Normalized Mean Error)^[4]作为评价指标, NME评价指标被广泛用于人脸对齐和重建中, 采用该评价指标有利于与NME的值越小表明效果越好, 如式(4)所示, ${y_g} $ 和 ${y_{{p}}}$ 分别为真实的人脸标记点和对应的预测点, 归一化因子 ${{d}}= $ $ \sqrt {{W_{\rm {bbox}}} \times {H_{\rm {bbox}}}}$ , 其中W和H分别为包围真实人脸图片的方框的宽和长.

$NME=\frac{1}{N}\sum\limits_{k=1}^N {\frac{{{{\left\| {{y_g} - {y_p}} \right\|}_2}}}{d}} $

(11)

图 6 人脸对齐效果图

结果如表2所示, 3DDFA方法在固有模型的限制下, 对各类姿态人脸的对齐效果会比PRN基于位置图回归的方式得出的模型效果差, 而本文的方法使用密集卷积模块构建网络, 在编码网络实现特征重用, 并构建新优化损失函数, 使得评价指标相对PRN略有优化. 其他方法的数据来源于各自所属论文.

表 2 多姿态人脸对齐归一化平均误差(%)

3.2.2 人脸重建实验结果分析

人脸重建的测试集同样使用AFLW-3D数据集, 部分效果图如图7所示, 其中第1列为各种姿态的人脸原图, 第2列和第3列为对应重建三维人脸模型在不同视角下的效果图. 为了对重建效果进行评估, 首先使用迭代最近点算法(ICP)^[17]对真实的三维人脸点云和模型输出的三维人脸点云进行配准, 然后用人脸外眼间距离作为归一化因子计算归一化平均误差. 我们对比了3DDFA, DeFA^[18]和PRN的归一化平均误差指标, 结果如表3所示, 相关对照数据来源于文献[7], 可见本文的方法有较好的效果.

4 结论与展望

本文提出了一种基于编解码方式的卷积神经网络, 实现了在不同人脸姿态条件下的人脸对齐和从单张二维人脸图片重建出三维人脸. 在网络架构部分使用密集卷积模块和转置卷积模块构建网络, 有效降低了模型的冗余度, 并结合图像结构相似度评价和特定面部权重作为损失函数, 提高了人脸对齐的精确度的和人脸重建的质量. 在测试数据集AFLW-3D上进行实验表明, 本文所提的网络模型优于之前的方法. 在今后的工作中, 本研究将继续在优化重建过程和提高重建精度上做出改进.

图 7 人脸重建效果图

表 3 人脸重建归一化平均误差(%)

参考文献

[1]	Cootes TF, Taylor CJ, Cooper DH, et al. Active shape models—Their training and application. Computer Vision and Image Understanding, 1995, 61(1): 38-59. DOI:10.1006/cviu.1995.1004
[2]	Matthews I, Baker S. Active appearance models revisited. International Journal of Computer Vision, 2004, 60(2): 135-164. DOI:10.1023/B:VISI.0000029666.37597.d3
[3]	Tzimiropoulos G, Pantic M. Optimization problems for fast AAM fitting in-the-wild. Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, NSW, Australia. 2013. 593–600.
[4]	Bulat A, Tzimiropoulos G. How far are we from solving the 2D & 3D face alignment problem? (and a dataset of 230, 000 3D facial landmarks). Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy. 2017. 1021–1030.
[5]	Blanz V, Vetter T. A morphable model for the synthesis of 3D faces. Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA. 1999. 187–194.
[6]	Zhu XY, Liu XM, Lei Z, et al. Face alignment in full pose range: A 3D total solution. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(1): 78-92.
[7]	Feng Y, Wu F, Shao XH, et al. Joint 3D face reconstruction and dense alignment with position map regression network. Proceedings of the 15th European Conference on Computer Vision. Munich, Germany. 2018. 557–574.
[8]	Jeni LA, Cohn JF, Kanade T. Dense 3D face alignment from 2D videos in real-time. Proceedings of the 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition. Ljubljana, Slovenia. 2015. 1–8.
[9]	Romdhani S, Vetter T. Estimating 3D shape and texture using pixel intensity, edges, specular highlights, texture constraints and a prior. Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA, USA. 2005. 986–993.
[10]	Güler RA, Trigeorgis G, Antonakos E, et al. DenseReg: Fully convolutional dense shape regression in-the-wild. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 2614–2623.
[11]	Yu R, Saito S, Li H X, et al. Learning dense facial correspondences in unconstrained images. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy. 2017. 4733–4742.
[12]	Jackson AS, Bulat A, Argyriou V, et al. Large pose 3D face reconstruction from a single image via direct volumetric CNN regression. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice, Italy. 2017. 1031–1039.
[13]	He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
[14]	Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA. 2017. 2261–2269.
[15]	Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861
[16]	Gu XF, Gortler S J, Hoppe H. Geometry images. ACM Transactions on Graphics, 2002, 21(3): 355-361. DOI:10.1145/566654.566589
[17]	Besl PJ, McKay ND. A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791
[18]	Liu YJ, Jourabloo A, Ren W, et al. Dense face alignment. arXiv preprint. arXiv: 1709.01442, 2017.