随着飞行模拟器的发展, 载人离心机因能实现持续的高过载模拟越来越引起飞行训练领域的重视, 在飞行模拟领域也得到越来越广泛的应用. 飞行模拟器的逼真度是评价飞行模拟器最重要的指标之一, 同时也能指导飞行模拟器的设计. 目前关于飞行模拟器的模拟逼真度评价主要有两方面的研究:
一类是飞行模拟器的综合逼真度评价, 这类评价方法主要针对视觉、操纵性和环境感知(声、光、温度、振动等)[1-4]等方面的模拟逼真度评价.
另一类研究主要通过感知误差来对模拟器控制算法优化的效果进行评价[5]. 即比较运动平台的模拟过载感知和目标过载感知, 依据这个误差量的大小来评价运动平台的运动学解算算法的优劣. 通过感知误差来对飞行模拟器的感知进行评价.
除了这两类外, 文献[6, 7]通过飞行员模型对飞行模拟器的逼真度进行评价. 文献[8]通过对飞行员操纵输出功率的相似性进行模拟逼真度评价.
现有的模拟器逼真度评价针对持续高过载模拟的应用场景主要存在以下不足: 1)离心式模拟器重点是模拟运动感知, 因此侧重于操纵等的模拟器逼真度评价模型不适用于离心式飞行模拟器; 2)运动感知具有特殊性. 仅仅通过误差量评价忽略了人体感知存在阈值等特性, 以此对运动学解算算法进行评价, 将不能精准有效指导运动学解算算法的优化.
本文针对上述情况, 结合人体对于运动模拟的特点, 采用模糊评价方法进行运动感知逼真度的评价.
1 逼真度评价原理飞行模拟器一般是在有限、安全的空间中模拟自由无限的运动环境, 所以通过飞行模拟器模拟真实的飞行物理量是不现实的, 但是可以通过飞行模拟器使得人体运动感知上的近似来实现对空中飞行的模拟, 这也是飞行模拟器的基本理论依据. 图1飞行模拟器运动感知模拟原理.
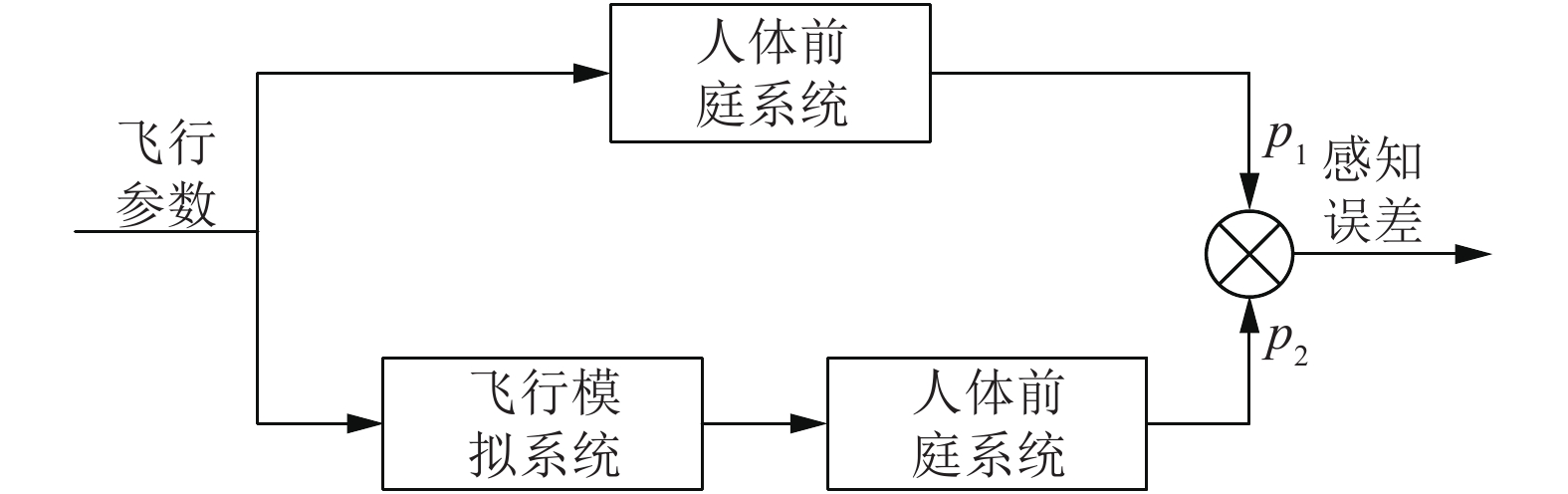
|
图 1 飞行模拟器运动感知模拟原理 |
人体的感知模型不等同于一般的传感器, 它存在一定的感觉阈值, 当线运动和角运动小于人体感觉阈值时, 人体感觉不到相关运动的存在. 这个特点对于人体的感知评价具有很重要的参考意义. 人体感知的门限[9]如表1.
因此在评价时, 阈值以下和阈值以上的误差对人体感知的影响不是线性关系的, 并且不同方向的感知阈值也不一样. 另一方面, 在人体感知的过载特别大, 大于一定上限的时候, 这时很可能发生过载引起的意识丧失(G-LOC)[10]. 这是因为过载对于人体前庭系统属于一种外力, 所以施加于人体前庭系统的过载是有一定的感知效果范围的. 经过以上分析, 人体前庭系统对过载的感知是有一定的敏感区域的, 在过载感知方面存在感知下限阈值, 也存在引起感知丧失的感知上限. 在建立科学有效的感知评价模型时需要考虑这两个因素.
| 表 1 人体运动感知阈值 |
2 运动感知逼真度评价模型
人体运动感知的评价不同于一般的标量评价, 过载和角速度均存在方向. 如果感知方向出现差错, 那么模拟的效果就很不理想, 模拟器的逼真度要被很严重的降低. 所以载人离心机的运动感知逼真度评价应该是结合方向、阈值等多方面的感知评价.
2.1 隶属度模型对于任意时刻的理想运动感知和实际运动感知误差, 依据不同误差区间的感觉体验, 评价集可设计为:
| $ V=\left\{\begin{array}{l} {\text{非常真实}}(\rm {HR}){\text{、}} {\text{比较真实}}\left(\rm {RR}\right){\text{、}}\\ {\text{一般真实}}\left({\rm {CR}}\right){\text{、}} {\text{不真实}}\left({\rm {NR}}\right){\text{、}}\\ {\text{非常不真实}}\left({\rm {HNR}}\right){\text{、}} {\text{方向错误}}\left({\rm {DE}}\right)\end{array}\right\} $ |
在设计飞行模拟器中, 如果感知在方向上出现差错, 会影响到飞行员的方向操纵判断, 所以方向评价对于飞行模拟判断是非常有必要的. 为了能突显出感知误差的方向特性, 将方向引入到感知误差中, 对感知误差作如下处理:
| $pe = \left\{ {\begin{array}{l} {{p_1}{p_2}\left| {\dfrac{{{p_1} - {p_2}}}{{{p_1}{p_2}}}} \right|,\;{p_1}{p_2} \ne 0} \\ {\left| {{p_1} - {p_2}} \right|,\;{p_1}{p_2} = 0} \end{array}} \right.$ | (1) |
其中, pe是评价模型输入, p1是模拟器理想运动感知, p2是模拟器实际运动感知.
为了能对运动感知效果有比较准确的评价, 本文采用模糊评价的方法, 建立系统的评价模型, 依据不同评价区间对逼真度的影响建立隶属度函数[11].
当感知误差为负的时候, 出现方向感知反向, 将严重影响感知逼真度, 隶属度函数选择为Z型:
| $f\left( {x;a,b} \right) = \left\{ {\begin{array}{l} {1,\;x \le a} \\ {1 - 2{{\left( {\dfrac{{x - a}}{{b - a}}} \right)}^2},\;a \le x \le \dfrac{{a + b}}{2}} \\ {2{{\left( {\dfrac{{x - b}}{{b - a}}} \right)}^2},\;\dfrac{{a + b}}{2} \le x \le b} \\ {0,\;x \ge b} \end{array}} \right.$ | (2) |
当感知误差在人体感知阈值以内的时候, 是模拟器的输出感知最理想状态, 此时在阈值内的感知误差都是最优的, 增强了评价界限设定的合理性, 此时的隶属度函数选择为钟型:
| $f\left( {x;a,b,c} \right) = \frac{1}{{1 + {{\left| {\dfrac{{x - c}}{a}} \right|}^{2b}}}}$ | (3) |
当感知方向相同, 但是绝对量的感知出现误差的时候, 应选择最常用的高斯型隶属函数:
| $f\left( {x;\sigma ,c} \right) = {{\rm e}^{\textstyle\frac{{ - {{\left( {x - c} \right)}^2}}}{{2{\sigma ^2}}}}}$ | (4) |
当感知的误差到极大, 不能接受或者评价没有意义的时候, 统一进行处理, 选择隶属度函数为S型:
| $f\left( {x;a,b} \right) = \left\{ {\begin{array}{l} {0,\;x \le a} \\ {2{{\left( {\dfrac{{x - a}}{{b - a}}} \right)}^2},\;a \le x \le \dfrac{{a + b}}{2}} \\ {1 - 2{{\left( {\dfrac{{x - b}}{{b - a}}} \right)}^2},\;\dfrac{{a + b}}{2} \le x \le b} \\ {1,\;x \ge b} \end{array}} \right.$ | (5) |
在隶属度函数参数设计的时候, 应满足如下条件:
1) 评语理想位置应满足隶属度函数处于峰值;
2) 某一函数的隶属度为1时, 其他隶属度函数的隶属度应接近或者等于零;
3) 隶属度的变化趋势符合当前评语的具体情况.
综上, 感知误差的隶属函数设计如图2, 其中
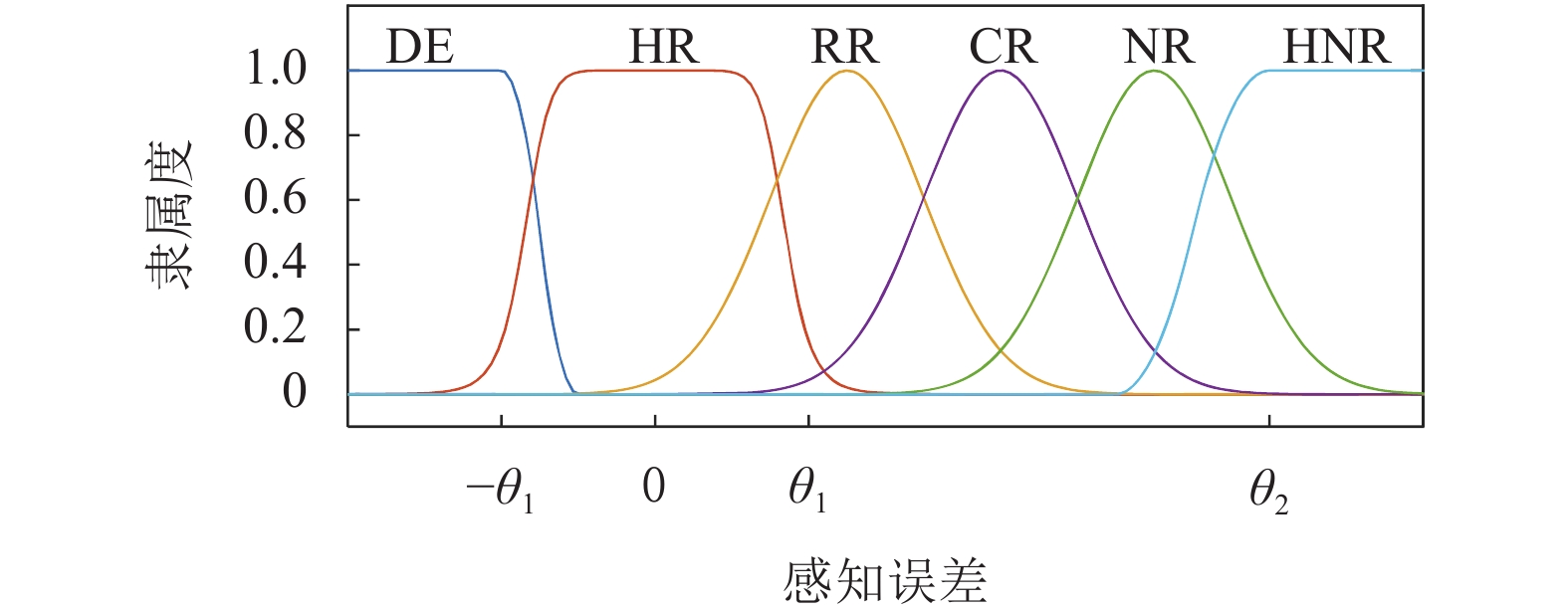
|
图 2 感知评价隶属度函数 |
2.2 有效度规则
大多数情况下, 同一输入存在多个评价结果, 一般采用最大隶属度原则[12]来确定, 即对于具体的评语集
| $R = {\max\nolimits_{1 \le i \le n}}\left\{ {{b_i}} \right\}$ | (6) |
但是最大隶属度原则是存在有效性的, 在评语集隶属度相差不大的情况下, 会使得评价结果不够理想. 所以, 为了使得评价结果更具有合理性, 采用有效度指标来进行最大隶属度原则判别, 有效度[13]的定义为:
| $\alpha = \frac{{n\beta - 1}}{{2\gamma \left( {n - 1} \right)}}$ | (7) |
其中,
通过对有效度定义分析可以发现, 有效度
| 表 2 低有效度评价规则 |
以上方法能得到某一个离散时间点的感知评价结果, 对于感知评价这显然是不够的, 对于某一次飞行任务或者一个飞行动作进行评价还需要在时间上进行统计分析.
| $E = \sum\limits_{i = 1}^n {{\mu _i}{P_i}} $ | (8) |
其中,
为了对模型的评价效果进行验证, 本文采用了一次爬升动作的Z向过载和一次盘旋下降动作的Y向过载进行分析, 将模拟器输出与预期感知作为模型输入, 对模拟器的运动模拟逼真度进行评价. 系统的输入如图3所示.
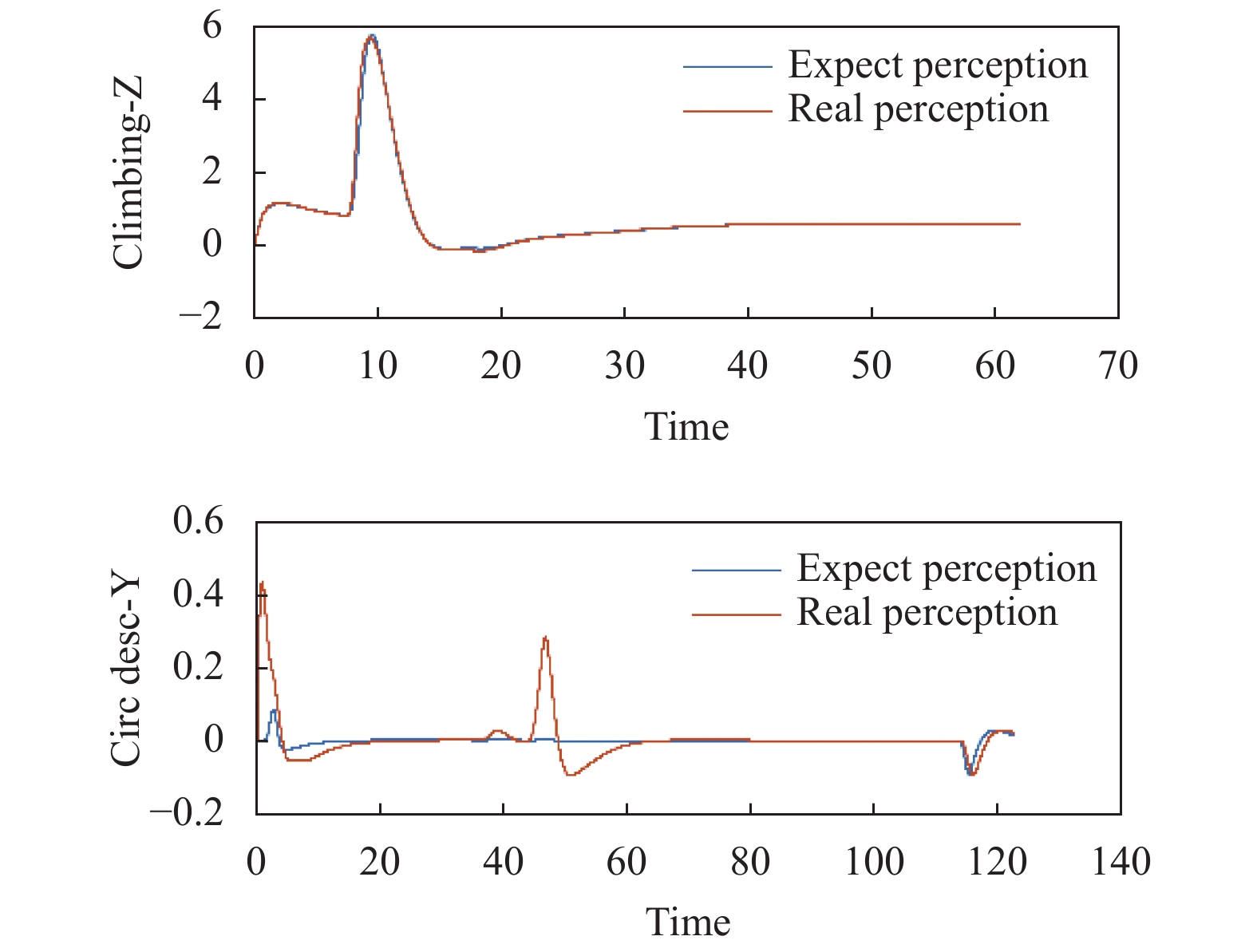
|
图 3 飞行模拟数据 |
对感知误差进行方向处理. 使得评价模型的输入具有方向相同或者相反的属性. 对案例中的真实感知和模拟器感知输出进行方向处理, 处理结果如图4.
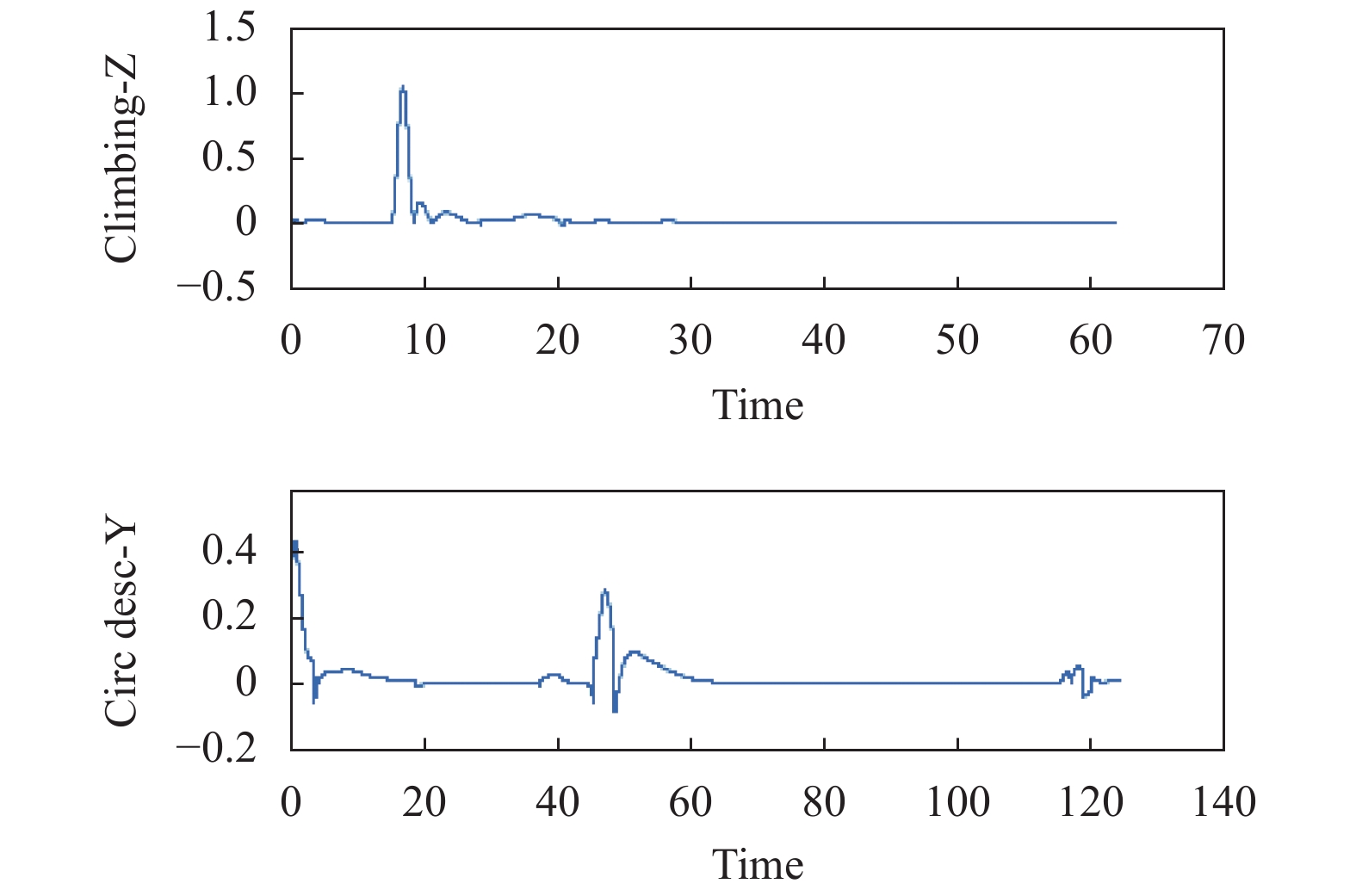
|
图 4 预处理结果 |
从处理结果可以看出, 在爬升这类难度不高的动作中, 模拟器的仿真结果整体是比较平稳的, 仅在8 s附近出现比较大的过载偏差. 盘旋下降的过载高频分量较多, 模拟效果的波动较为明显, 但是不存在较大的感知误差.
依据评价模型中提到的隶属度函数设计原则, 设计参数值如下:
(1)当感知方向相反的时候, 评价为DE, 采用的是Z型隶属度函数, 参数
(2)当评价为HR时, 采用钟型函数, 依据人体感知阈值特性, 参数
(3)当评价为RR, CR, NR时, 统一采用高斯分布类似处理, 考虑与其他隶属度函数的耦合关系, 可以将参数
(4)当评价为HNR时, 采用S型隶属度, 参数
如果某一个评价输入同属于多个隶属度函数的时候, 尽管最大隶属度始终存在. 但是当最大和次大隶属度接近时, 仅仅通过最大隶属度的原则来判别, 会降低一部分结果的客观性. 有效度的大小反映了隶属度的接近程度. 评语结果数
| $\alpha = \frac{{6\beta - 1}}{{10\gamma }}$ | (9) |
隶属度有效度是为了解决隶属度相近的时候的评价结果, 同一的评价输入如果同属于两个相近的隶属度函数, 这时两个函数的隶属度均在0.5左右, 将
以爬升和盘旋下降动作的误差作为输入, 在隶属度函数上进行评价计算, 并对时域上的评价结果进行统计, 结果如图5.
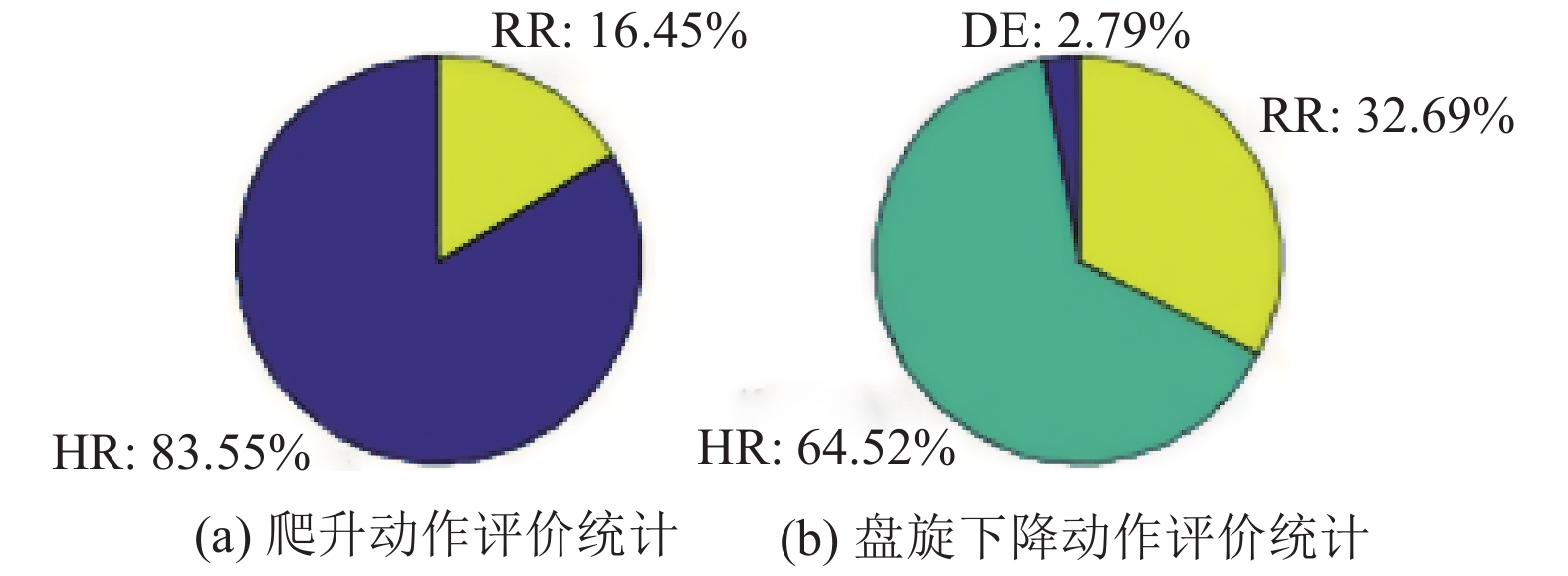
|
图 5 评价时长占比统计 |
两个飞行动作的模拟评语为HR的占大多数, 但是也看出机动要求比较高的动作中, 模拟出现了比较大的波动, 甚至出现了负牵引(DE)的情况.
为了得到统一直观的评价结果, 还需要对评语集进行效能值设计, 如果仅仅采用专家评分的方法来进行各个评语的指标设计, 有很强的主观性. 层次分析法是将定性问题转化为定量问题的有效途径, 所以可以采用层次分析法进行评分设计. 各个评语的评分值可以类比权重方法进行设计, 也就是权重越弱, 评分越低. 因此构造判断矩阵如下:
| $A = \left[ {\begin{array}{*{20}{c}} 1&{\dfrac{1}{9}}&{\dfrac{1}{7}}&{\dfrac{1}{5}}&{\dfrac{1}{3}}&1 \\ 9&1&7&5&3&9 \\ 7&{\dfrac{1}{3}}&1&3&5&7 \\ 5&{\dfrac{1}{5}}&{\dfrac{1}{3}}&1&3&5 \\ 3&{\dfrac{1}{7}}&{\dfrac{1}{5}}&{\dfrac{1}{3}}&1&3 \\ 1&{\dfrac{1}{9}}&{\dfrac{1}{7}}&{\dfrac{1}{5}}&{\dfrac{1}{3}}&1 \end{array}} \right]$ |
计算得权重关系为:
| $ w = \left[ {0.030\;0.529\;0.229\;0.120\;0.062\;0.030} \right]$ |
最大特征根
| ${E_{cbZ}} = \sum\limits_{i = 1}^n {{\mu _i}{P_i}} = 0.4797$ | (10) |
| ${E_{cdY}} = \sum\limits_{i = 1}^n {{\mu _i}{P_i}} = 0.4170$ | (11) |
按照该案例中的评估, 最优的评估结果, 即全部评价为HR, 对应的评分为0.529. 所以最后的评价结果以0.529为最佳结果进行百分制转换, 得到评价结果:
| ${E_{cbZp}} = \frac{{{E_{cbZ}}}}{{{E_b}}}*100{\rm{ = }}90.68$ | (12) |
| ${E_{cdYp}} = \frac{{{E_{cdY}}}}{{{E_b}}}*100{\rm{ = }}78.83$ | (13) |
从评价结果可以看出, 在某型模拟器中, 对爬升动作Z向的模拟逼真度很高, 但是盘旋下降动作的Y向的模拟逼真度相对较低. 从评价过程分析, 主要是因为存在较多的RR存在, 并且还存在少量的负牵引出现, 影响了评价结果. 也反映了本文中的评价模型能够完成运动感知的模拟逼真度评价, 能对不同模拟效果进行有效区分.
4 总结本文采用模糊评价的方法, 以人体感知阈值为主要标准设计模糊评价的隶属度函数. 对原始数据进行方向处理, 使得评价模型能对模拟中出现的负牵引现象进行区别评价. 最后采用最大隶属度函数有效度置信区间对评价模型进行严格化处理. 通过案例仿真, 对爬升动作Z向和盘旋下降Y向过载模拟结果进行评价, 本文的评价模型能够对运动感知的模拟逼真度进行评价, 从而有效评价运动仿真系统的模拟逼真度.
| [1] |
官建成, 屈香菊. 综合评价飞行模拟器的一种方法. 飞行力学, 1994, 12(3): 73-80. |
| [2] |
林以军, 王鸣歌, 范万岗, 等. 基于模糊评判法的飞行模拟器逼真度评估. 科学技术与工程, 2008, 8(2): 543-546. DOI:10.3969/j.issn.1671-1815.2008.02.057 |
| [3] |
胡文, 刘红军. 基于灰色理论的飞行模拟器逼真度评估. 兵工自动化, 2007, 26(4): 18-20. DOI:10.3969/j.issn.1006-1576.2007.04.009 |
| [4] |
王远达, 宋笔锋, 李小奇, 等. 飞行模拟器逼真度的实用评价方法. 海军工程大学学报, 2005, 17(6): 53-57. DOI:10.3969/j.issn.1009-3486.2005.06.010 |
| [5] |
冯云龙. 基于模糊优化洗出算法的直升机模拟器运动控制研究[硕士学位论文]. 长春: 吉林大学, 2016.
|
| [6] |
Gao J, Zheng ST, Li HR. Assessment of flight simulator fidelity for pitch task. Key Engineering Materials, 2011, 460–461: 569-573. |
| [7] |
Hess RA, Marchesi F. Analytical assessment of flight simulator fidelity using pilot models. Journal of Guidance, Control, and Dynamics, 2009, 32(3): 760-770. DOI:10.2514/1.40645 |
| [8] |
李蕊, 姜洪洲. 闭环逼真度评价的洗出算法参数优化. 现代制造工程, 2010(6): 55-59. DOI:10.3969/j.issn.1671-3133.2010.06.016 |
| [9] |
Asadi H, Lim CP, Mohamed S, et al. Increasing motion fidelity in driving simulators using a fuzzy-based washout filter. IEEE Transactions on Intelligent Vehicles, 2019, 4(2): 298-308. DOI:10.1109/TIV.2019.2904388 |
| [10] |
Kim S, Nam W, Kil H, et al. Formal verification of a gravity-induced loss-of-consciousness monitoring system for aircraft. Computing in Science & Engineering, 2014, 16(5): 96-103. |
| [11] |
Yao K. Conditional uncertain set and conditional membership function. Fuzzy Optimization and Decision Making, 2018, 17(2): 233-246. DOI:10.1007/s10700-017-9271-2 |
| [12] |
Gao JQ, Yin XL, Hou ZF. Research on fuzzy recognition method of boiler four-tube leakage. Proceedings of 2011 2nd International Conference on Intelligent Control and Information Processing. Harbin, China. 2011. 391–393.
|
| [13] |
郭东星, 刘桂芬, 何大卫. 有效度在最大隶属原则中的价值. 现代预防医学, 2005, 32(5): 429-430, 508. DOI:10.3969/j.issn.1003-8507.2005.05.007 |
 2021, Vol. 30
2021, Vol. 30


