2. 中原工学院 前沿信息技术研究院, 郑州 450007
2. Research Institute of Frontier Information Technology, Zhongyuan University of Technology, Zhengzhou 450007, China
BLAS (Basic Linear Algebra Subprograms)基础线性代数库是一个基本线性代数操作的数学函数标准, 支撑着许多计算机应用领域的数值线性代数计算, BLAS一般分为三级, 一级主要完成向量与向量之间的操作; 二级主要完成向量与矩阵之间的操作; 三级主要完成向量与向量之间的操作. 其不仅被广泛应用于科学计算领域, 并且在深度学习方面, 底层调用BLAS库进行加速运算已经十分常见了. 例如基于矩阵类的深度学习有百分之90或更多的时间是通过BLAS来进行计算的, 因此一个高性能的BLAS库具有十分重要的意义. 目前各大主流处理器厂商都对其硬件平台做了深度优化工作, 例如Intel的MKL (Math Kernel Library, 数学核心库)、AMD的ACML (AMD Core Math Library)、以及在Nvidia上使用的CuBLAS等.
申威1621处理器基于第三代“申威64”核心的国产高性能多核处理器, 主要面向高性能计算和中高端服务器应用. 设计目标主频为2.0 Ghz, 单芯片集成了16个64位申威处理器核心, 双精度浮点性能可达512 Gflpos. 申威1621处理器具有16核心共享32 MB的三级Cache, 支持256位SIMD指令, 可以在最大程度上提升系统的数据级并行.
目前来说, BLAS三级函数的研究已经较为成熟[1], 因此本文的研究内容主要在于优化工作相对较少的BLAS一级函数上. 首先BLAS一级函数属于访存密集型函数, 性能主要受限制于处理器本身的缓存大小和访存带宽, 对这些函数优化难度较大[2]; 其次在于计算数据规模和排布的不确定性, 又给优化工作带来新的难题. 目前对于BLAS一级函数的优化方法较为单一, 大多集中在使用指令优化方面, 通过利用数据预取以及向量化来提升访存性能, 而在使用多线程优化方面, 仅仅开启多线程进行计算, 但是对于多线程使用的线程数量并没有加以调控, 而是把这项任务交给了用户来决定[3], 这对于用户来说使用较为不便, 因此需要一套完成的优化方案来有效提升BLAS一级函数性能, 提高用户的便捷性. 目前GotoBLAS仅仅对AXPY, SWAP, SCAL三个主要函数实现了多线程并行化, 本文选取了其中较为复杂的函数AXPY为例进行优化分析.
本文主要针对申威1621处理器进行BLAS一级函数的优化研究工作. 其中第1节是引言, 介绍了平台信息与本文工作的意义; 第2节以BLAS一级函数中的典型函数AXPY为例, 介绍一级函数特点; 第3节介绍了基于单核的AXPY函数优化方法; 第4节介绍了多线程AXPY优化设计; 第5节为实验, 与开源的GotoBLAS[4]进行性能比较; 最后是总结与展望.
2 BLAS一级函数AXPY概述BLAS一级函数主要完成了标量与向量, 向量与向量之间的操作. 由于BLAS一级函数之间的相似性, 我们以函数AXPY(向量乘加)为例, 来说明一级函数的特点. AXPY函数实现了式(1)中的功能:
| $ {{Y}} = alpha*{{X}} + {{Y}} $ | (1) |
其中, alpha为标量, X, Y为向量. AXPY的计算复杂度为O(N), 从公式中可以看出, 在每个计算周期内, 有3次访存内存和2次计算操作, 计算访存比高达2:3[5]. 即使进行循环展开和指令重排等优化, 也无法将访存开销隐藏在计算过程中, 因此要尽可能地提高内存带宽的利用率, 由此来提高函数性能.
AXPY函数的计算访存比高达2:3, 能否达到访存带宽的上限将会是衡量BLAS一级函数优化效果的一个重要指标. 根据计算机组成结构, 访存带宽可以分为两部分, 高速缓存带宽即L2 Cache, 和内存带宽. 当数据规模小于L2 Cache时, 可以达到一个较高的性能水平. 当数据规模大于L2 Cache时, 访存性能会产生一个急剧下降, 此时函数性能较差.
目前GotoBLAS在申威1621上的BLAS一级函数实现方式是最基础的版本, 除了编译器优化外, 没有进行任何的其他形式优化, 该版本在1621平台上所取得的性能仅为8014 Mflops, 远远不能满足应用对于程序性能的需求, 因此要根据函数特定设计一套高效的优化方案来提升函数性能.
3 AXPY函数单核串行优化针对1621平台, 本节描述了AXPY函数单核高性能优化方案, 该方案基于AXPY函数访存密集型函数的特点, 再结合申威1621处理器平台特性, 实现了该平台的上高性能AXPY函数.
3.1 256位的SIMD向量指令申威1621处理器提供了256位SIMD向量拓展指令. 针对AXPY函数访存密集型特点, 能够最大程度发挥该平台访存能力. 为实现高性能的AXPY函数, 我们选择使用SIMD向量乘加指令、SIMD向量访存指令以及SIMD向量复制指令来进行优化, 提高数据并行程度. 基于AXPY函数, 任务数据可以分为两类, 一类是计算步长为1时的连续数据另一类是计算步长不为1时的离散数据, 针对这两种不同的数据, 处理方式也有所不同.
在计算步长为1的情况下, SIMD拓展指令能够将内存地址连续的数据多次装载, 转变为一次全部装在到向量寄存器. 只用一条SIMD拓展指令能够实现并行处理SIMD向量寄存器中的所有数据. 以双精度为例, 每个数据元素为8字节、64位, 配合申威1621处理器提供的长度为256位SIMD访存指令使用时, 可以如图1所示, 每次从内存空间顺序读取4个X向量元素或Y向量元素放入浮点向量寄存器中去. 针对标量元素alpha则使用向量复制指令, 将其拓展成4份再存入浮点向量寄存器中, 这样即可完成对所需计算数据进行向量打包, 便于下一步利用向量运算指令展开计算.

|
图 1 连续数组向量化示意图 |
申威1621平台提供256位的SIMD乘加指令, 可以在1.5个时钟周期内同时完成乘法和加法操作. 经过上一步将数据打包为向量块之后, 我们可以直接使用乘加指令来完成整个计算操作. 这样相对比与原本的计算方式, 计算相同数据量的情况下, 可以减少12计算条指令执行时间, 从而提升函数性能.
当默认步长不为1时, 任务数据并不连续, 无法直接使用SIMD向量化指令进行运算. 对于此类不连续数据访问方式, 姚金阳等人[6]提出了一种间接数组索引的向量化方法, 该方案通过引入一个间接数组的方式对数据进行重排序, 重排方法如图2所示, 经过重排打包之后, 利用向量乘加指令进行运算. 如果使用此方案进行向量化优化, 我们对其进行收益进行评估.

|
图 2 间接数组向量化示意图 |
Step 1. 载入数据时, 要对数据进行一次“预处理”, 每次访存都会引入一条新的载入指令, 把需要计算的X和Y数据全部载入共计引入了新的8条载入语句.
Step 2. 计算时, 由于数据已经打包成向量块, 使用一条向量乘加指令即可完成数据的计算, 共计减少了7条计算指令.
Step 3. 存储数据时, 要对数据再次进行一次“尾处理”, 将已经打包的向量块拆分存储并存储到数据原本的位置, 共计引入4条拆分指令.
综上, 对于原本串行执行, 使用向量化指令进行计算会多引入5条指令. 向量化优化收益为负, 因此对于步长不为1的情况, 仍选择使用串行执行即可.
3.2 访存优化进行访存优化的方法主要有两种: 一是加快访存速度, 二是隐藏访存延迟, 数据局部性优化, 例如循环展开, 数据预取, 指令重排等方式. 1621处理器的平台的访存速度是由硬件平台所决定的, 我们无法对其做出更改, 因此本文选择从软件优化的方式出发, 利用循环展开、数据预取和指令重排的方式并结合申威1621平台特点进行优化.
循环展开是编译器优化的基本方法之一, 循环展开之后, 可以增加最内层循环的单次循环指令数目. 这样做的优势有两方面, 一方面从硬件看, 单次循环内, 指令数目的增加, 可以更好地利用硬件资源, 更多的指令便于硬件流水线发挥作用, 同时CPU保留栈等硬件资源也可以得到充分的利用; 另一方面从软件的角度看, 更多的指令便于将指令进行重排, 避免出现访问和计算同时使用相同的寄存器, 从而出现流水线停顿[7]. 考虑访存延迟、计算指令的排布以及寄存器的数量, 将循环展开4次即可.
数据预取是将取数据和用数据人为的分开, 使它们能够充分的并行执行, 而不会因为等待数据停止流水. 针对AXPY函数的计算特点, 每两次访问进行一次乘加计算, 乘加计算需要等待这两次访问完全结束才能开始执行
数据的依赖关系并不利于流水线的充分使用. 访存与计算之间, 数据存在依赖关系, 要先将数据存放在寄存器中之后才能再参与运算. 因此如果在核心计算开始时, 再进行数据载入时, 会因为计算指令等待访存指令完成再进行执行, 因而引发了流水线的停顿. 为解决流水线停顿的问题, 本文在核心计算开始之前进行一次数据提前载入, 这样当核心计算开始时, 本轮计算所用数据已经完全载入到寄存器之中, 计算所用数据不会因为访存而产生依赖关系, 同时我们在计算本轮结果时, 载入下一轮计算所需数据, 这样将计算数据与访存数据分开, 解除计算与访存数据之间的依赖关系.
即使进行了循环展开和数据预取的优化, 但核心计算循环内, 访存指令数量仍然远大于计算指令数量, 计算延迟无法掩盖访存延时, 因此在指令重排的时候, 可以考虑另外一种排布方式, 将计算时间隐藏在访存之中, 这样可以达到函数的理论性能上限. 申威1621处理器提供了2条浮点流水线, 可同时并行指令两条浮点指令, 同时提供了F0—F32共32个向量寄存器. 基于以上条件, 本文重新设计了核心函数的指令排布.
在核心函数的设计中, 应当遵循以下几条原则: (1)最内层循环应当展开够一定次数, 访存指令可以充分掩盖计算指令, 防止计算延迟的出现; (2)硬件提供了两条流水线, 避免将当前指令的目的寄存器作为下一条指令的源寄存器, 避免出现流水线停顿的情况; (3)尽可能地利用指令之间的间隙, 通过对1621平台的指令周期测试, 根据不同执行需要指令的指令周期来进行合理排布, 减少的总的指令周期时长[8].
BLAS一级函数AXPY完成操作较为简单, 在核心计算函数的编写中, 需要用到的指令种类较少, 通过对其测试得到了表1中的结果. 从表1中可以看出, 每条访存执行周期内, 可以完成两条计算指令的执行. 由于AXPY函数计算指令远远少于访存指令, 如果正常执行一条计算指令和一条存储指令, 则会由于数据的依赖关系需要等待计算指令结束之后, 再进行存储指令的执行, 不利于两条执行并行执行. 因此我们选择如图3的指令重排方式, 在执行计算指令的时候, 同时执行数据载入指令, 载入下一轮计算所需数据. 这时由于计算指令执行所需时间仅为1.5个CPU周期, 但访存指令需要3个CPU执行周期, 计算执行会比访存指令更早的结束执行. 为了避免当前指令的目的地址作为下一条指令源地址情况的出现, 我们在排布第3条指令的时候仍进行数据载入操作, 这时流水中同时执行的是两条数据载入指令, 之后再执行数据存储操作. 这样的指令排布保证了一条计算指令所需时间完全隐藏在了访存指令执行时间之中, 并且两条流水线可以得到充分的利用.
| 表 1 向量指令执行所需周期数 |

|
图 3 指令重排示意图 |
为了减少数据之间的依赖, 本文选择了预先载入计算数据, 并在计算的时候载入下一次计算所用数据, 这种方式虽然解除了计算与访存之间数据的依赖关系, 但是引入了更多了临时寄存器[9], 由原本每次计算仅需2个寄存器增加到每次计算需要4个寄存器. 这时候可用寄存器的数量就限制了可以循环扩展的最大次数. 申威1621处理器提供了32个向量寄存器, 可自由使用向量寄存器为31个, 在寄存器的限制下, 循环展开的最大次数被限制7次以内. 为了减少边际数据的处理, 我们选择将循环展开次数定为4次.
由于对核心计算进行了4次循环展开, 因此每次内层循环中由6条计算指令和12条访存指令组成. 根据上述原则对循环进行指令重排, 如图3所示为指令重排前后的指令流水. 进行指令重排之后, 充分发挥了申威1621处理器浮点双流水的特点, 将6条计算指令耗时隐藏在12条访存指令之中, 从原本的每次核心循环执行完成需要的15个时钟周期缩减到11个时钟周期, 此时函数性能完全由访存性能决定, 基本达到了函数的理论峰值.
4 AXPY函数多核优化设计 4.1 并行化多线程并行是一种常见的优化方式[10], 在没有数据依赖以及不超过总线带宽的基础上, 可以有效地提高函数的访存性能, AXPY函数主要进行向量-向量之间的运算, 理论上线程之间没有数据依赖, 因此AXPY函数具有天然的负载均衡. 对于函数AXPY来说, 进行并行化的优化并不复杂, 由于向量数据之间没有关联性, 我们可以使每个计算核心运行一个线程, 每个线程的函数优化设计沿用上一章单核函数优化设计的方案即可.
对于需要计算任务数据的划分, 根据AXPY函数多为向量数据, 易于分段且数据规模较为规整的特点. 不需要对数据进行前期处理, 在并行区开始之前主线程执行静态任务调度, 即可保证各线程之间的负载均衡[11]. 由于AXPY函数性能的瓶颈在于内存带宽, 当达到带宽极限时再增加线程只能导致资源冲突, 反而会使AXPY函数性能下降. 为此本文专门设计了线程自动分配函数来保证不会因为线程数量而影响到函数的性能.
4.2 线程分配考虑到AXPY函数的性能主要受限于访存带宽, 在访存带宽允许的情况下, 尽可能多的开启线程会一定程度上提升函数的性能. 当性能达到带宽上限时, 再增加线程的数量只会造成数据的争夺[12], 从而影响函数性能. 因此, 开启线程数量主要取决于1621处理器能达到的最大带宽.
根据任务规模, 我们可以将带宽分为两类, 一类当任务数据规模小于L2 Cache时的高速缓存带宽, 另一类是任务规模大于L2 Cache的内存带宽[13]. 为了帮助分析开启不同任务规模需要开启线程的数量, 利用Stream带宽测试工具对1621处理器进行带宽测试[14], 根据测试结果进行合理的线程分配.
利用Stream带宽测试工具, 我们测试了在大页缓存范围内, 不同线程的访存带宽能力. 通过图4的测试结果, 分析可得, 在高速缓存内, 随着线程数量的增加, 访存能力逐渐提升, 直到开启到12线程的时候, 访存带宽达到顶峰, 再增加线程数量, 只会增加线程之间带宽的争夺, 降低了访存的性能. 因此根据上文对缓存方式的分类再结合Stream带宽测试结果, 我们对线程进行如下划分.

|
图 4 线程带宽测试 |
1) 当任务规模小于L2 Cache时, 数据可以全部载入到L2 Cache中, 此时的访存带宽远远高于架构本身的真实带宽, 单线程优化后的访存带宽不足以达到此时的访存带宽, 在此阶段开启多线程, 可以最大的提升函数性能. 当数据规模较小时, 开启线程的花销会大于本身线程计算所用花销, 这样不利于性能的提升此时我们选择开启较小的线程数, 使用单线程进行计算. 随着数据规模的逐渐增大, 开启更多的线程数量来获取更多的性能, 根据带宽测试结果, 最大使用线程数量限制在12线程即可.
2) 当任务规模大于L2 Cache时, 此时访存带宽为架构本身真实带宽, 带宽较小, 只需将带宽全部跑满即可达到此时的最佳性能, 如果再增加线程数量, 只会降低函数性能. 根据Stream带宽测试结果表明, 使用SIMD优化之后开启双线程即可跑满带宽, 再增加线程数量只会降低函数性能. 因此在这种情况下, 开启双线程即可获得最优的性能.
综合以上限制条件, 针对线程开启情况设计了图5所示的多线程使用方案, 通过此方式来调节线程数量, 提升多线程对函数的优化性能.
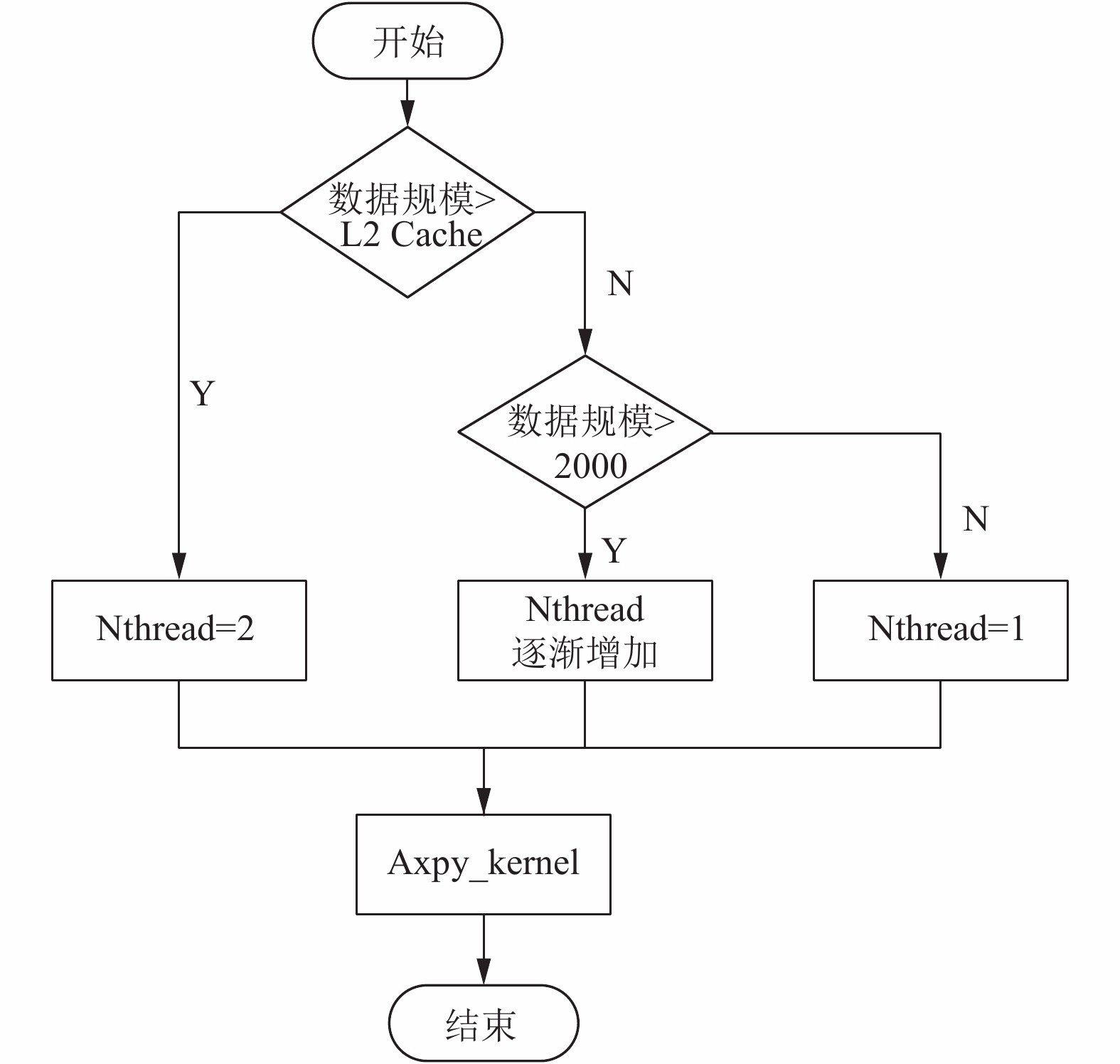
|
图 5 线程自动分配流程 |
5 性能测试与分析
申威1621处理器作为新一代的国产高性能多核平台, 性能指标较为优异, 作为本文的实验平台, 其各项参数指标如表2所示.
| 表 2 实验环境 |
针对AXPY函数的特点, 本文进行了一系列的对比测试, 首先利用Stream带宽测试工具, 测试了访存带宽测试, 以检测到的带宽作为对比参考. 其次为了更好地测得单线程与多线程的优化效果, 我们选择了不同的测试数据集来进行分别进行测试.
针对单核单线程的测试来说, 我们选取了数据规模从1000到10000, 步长为1000的共计10组数据进行测试. 实验结果如图6所示, 使用向量化技术优化之后, 相对原GotoBLAS实现平均2.73倍性能提升, 经过循环拓展和指令重排之后, 性能提升从原本的2.73倍提升至4.36倍.

|
图 6 单核优化性能测试结果 |
对于多核多线程的优化测试, 相对于单线程的测试不同, 多线程我们选择更大范围和规模的数据来进行测试, 并和单线程测试结果进行对比. 实验结果如图7所示, 相对比于申威平台单线程优化方案而言, 多线程最高加速比可达3.91, 平均加速比为2.18.

|
图 7 多线程优化测试对比结果图 |
图8为原版单线程与原版使用多线程的性能对比图, 从图中数据可以看出, 原版多线程相较于原版单线程最高加速比为3.29, 平均加速为1.8. 加速效果低于我们针对多线程进行线程分配之后的优化效果, 结合上面我们使用线程分配函数之后的优化结果可以得出结论, 我们设计的线程自动分配函数优化了因为线程争夺对性能产生的影响, 一定程度上提升了函数的性能.
6 总结与展望本文首先说明了BLAS一级函数的作为访存密集型函数的特点, 并针对其特点, 结合国产申威1621多核平台的架构特征, 设计了一套基于该平台的BLAS一级函数优化方案. 本方案首先分析了单核单线程的优化方法, 运用了循环展开, 指令重排等基于该平台的优化技术, 接着分析了基于多核多线程的优化方法, 提出了负载均衡和线程自动分配机制. 在性能测试中, 基于申威1621平台上经过优化的AXPY函数性能, 在单核情况下, 对比原GotoBLAS, 实现了平均加速比4.36, 多核12线程方案的平均加速比为9.5, 达到预期优化效果.
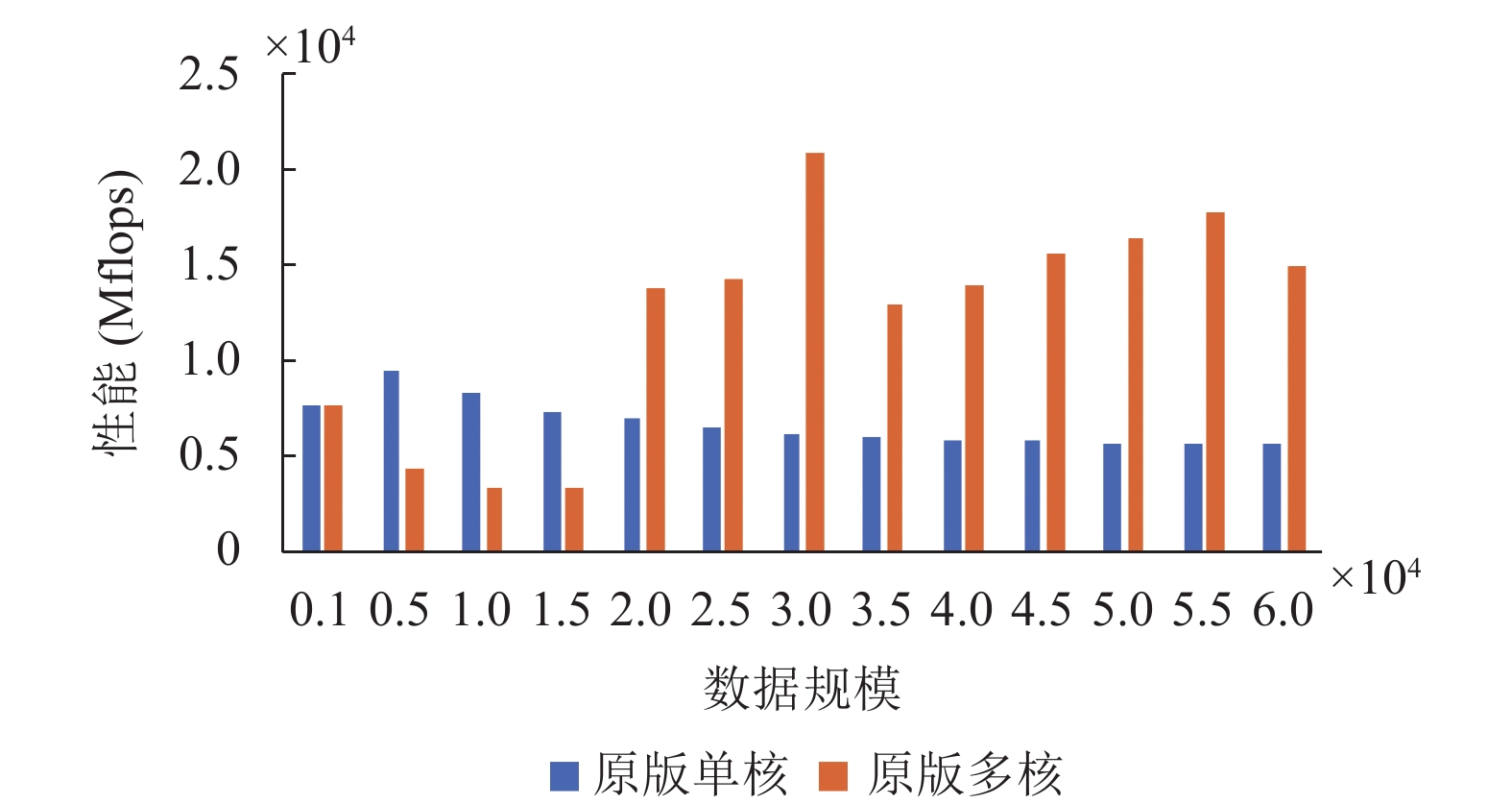
|
图 8 原版单核与多核性能对比图 |
本文主要考虑了自动线程分配机制在申威平台的实现方案, 因此在普适性应用时, 其他机器的L2 Cache可以直接获取到, 但是Cache中访存最大带宽无法直接得到, 需要通过Stream带宽测试, 但目前通用的Stream提供的带宽测试并没有使用SIMD指令来提高数据吞吐量, 如果编译器在编译时, 无法进行自动向量化优化, 那么这样测试所得的数据与实际应用中有较大差别, 因此仍需要一个专用带宽测试工具来测试出实际带宽, 在此基础上进行数据填充, 后续工作中将对这些做进一步研究.
| [1] |
张先轶, 王茜, 张云泉. OpenBLAS: 龙芯3A CPU的高性能BLAS库. 2011年全国高性能计算学术年会(HPC china2011)论文集. 济南, 中国. 2011. 1–9.
|
| [2] |
孙家栋, 孙乔, 邓攀, 等. 基于申威众核处理器的1、2级BLAS函数优化研究. 计算机系统应用, 2017, 26(11): 101-108. DOI:10.15888/j.cnki.csa.006045 |
| [3] |
陈少虎, 程豪, 张云泉, 等. BLAS库在多核处理器上的性能测试与分析. 2010年全国高性能计算学术年会(HPC china2010)论文集. 北京, 中国. 2010. 46–53.
|
| [4] |
Goto K, van de Geijn RA. Anatomy of high-performance matrix multiplication. ACM Transactions on Mathematical Software, 2008, 34(3): 12. |
| [5] |
苏波, 李凯, 徐志广, 等. 龙芯2F上的访存优化. 计算机系统应用, 2010, 19(1): 171-175. DOI:10.3969/j.issn.1003-3254.2010.01.038 |
| [6] |
姚金阳, 赵荣彩, 王琦, 等. 面向间接数组索引的向量化方法. 计算机科学, 2018, 45(9): 220-223, 236. |
| [7] |
许瑾晨, 郭绍忠, 黄永忠, 等. 面向异构众核从核的数学函数库访存优化方法. 计算机科学, 2014, 41(6): 12-17. DOI:10.11896/j.issn.1002-137X.2014.06.003 |
| [8] |
吴文文. 面向深度学习的GPU访存优化研究[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [9] |
张明. 龙芯平台上高性能计算的性能优化关键问题研究[博士学位论文]. 合肥: 中国科学技术大学, 2017.
|
| [10] |
张华亮, 黄启印, 吴少校. 基于龙芯3A2000处理器的高性能Goto BLAS库的实现. 高技术通讯, 2016, 26(10–11): 825-832. |
| [11] |
张帅, 李涛, 王艺峰, 等. 细粒度任务并行GPU通用矩阵乘. 计算机工程与科学, 2015, 37(5): 847-856. DOI:10.3969/j.issn.1007-130X.2015.05.001 |
| [12] |
Jang D, Schaa D, Mistry P, et al. Exploiting memory access patterns to improve memory performance in data-parallel architectures. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(1): 105-118. DOI:10.1109/TPDS.2010.107 |
| [13] |
Sung IJ, Stratton JA, Hwu WMW. Data layout transformation exploiting memory-level parallelism in structured grid many-core applications. Proceedings of the 2010 19th International Conference on Parallel Architectures and Compilation Techniques. Vienna, Austria. 2010. 513–522.
|
| [14] |
张广飞, 侯锐, 张科, 等. 内存系统模型与性能分析. 第十七届计算机工程与工艺年会暨第三届微处理器技术论坛论文集(下册). 西宁, 中国. 2013. 32–43.
|
 2021, Vol. 30
2021, Vol. 30



