1 引言

近些年来, 元启发式算法中最具代表性的范例之一: 群智能(SI)算法, 越来越受到广泛的学者欢迎. 其各个方向的研究成果已运用到计算机、图画、数学、决策控制等众多领域中, 例如: 机场调度、风力发电优化等. 群智能的概念最早是在1993年由Bonabeau等提出, 其灵感主要来自于自然中的群体工作的集体或系统. 例如受蚂蚁通过信息素记住曾经去过的地方的行为方式启发, Dorigo等学者提出蚁群优化(ACO)^[1]; 受鸟群寻找食物的社会行为启发, Kennedy等学者提出粒子群优化(PSO)^[2]. 之后, 越来越多优异的群智能算法被学者们提出, 例如灰狼蝙蝠(BA)算法^[3]、人工蜂群(ABC)算法^[4]、萤火虫(FA)算法^[5]、蜻蜓(DA)算法^[6], 以及本文要讲述的由Wang等学者提出的君主蝶优化(MBO)算法^[7]等等.

君主蝶优化算法(Monarch Butterfly Optimization, MBO)是由Wang等学者经过模仿君主蝶在自然界中的迁移行为于2015年提出的一种元启发式算法, 该算法可用以处理函数、陈列组合等经典优化问题, 具有相较于其他算法可以在大多数基准测试函数上找到更优值的能力. 在君主蝶优化算法中, 所有个体都被理想化, 并且只栖息在两个地区, 这里称为子群一(LandP1)和子群二(LandP2). 君主蝶的位置以两种方式进行更新, 分别为迁移算子(子群一)与调整算子(子群二). 当然也能同时实现两种算子, 这体现了其并行处理的功能, 可以通过调节二者关系对算法的收敛性与多样性进行平衡性调整. 本文从MBO寻优过程出发, 注意到MBO易陷入局部最优的问题, 本文使用Logistic混沌映射^[8]扰动当前种群中的最优解以增强其跳出局部最优的能力. 还注意到迁移算子产生的子代受其父代影响过大^[9], 不利于其更为多样化的全局搜索, 本文优化了迁移算子中子代传递的方式, 使其受到影响源更多. 本文提出的新算法, Logistic混沌映射君主蝶优化算法(Monarch Butterfly Optimization with Logistic Chaotic Map, LCMMBO). 通过随机抽取Benchmark库中的10个基准测试函数对其进行数值模拟实验验证, 发现其相较于标准MBO算法与CABC算法^[10]在处理高维的优化问题时表现出良好的性能, 不仅鲁棒性优异, 而且跳出局部最优的能力强.

2 君主蝶优化算法

在MBO中, 所有君主蝶的生成位置仅在两个子群内, 它们以两种方式更新位置, 分别是迁徙算子生成新的位置, 可以通过迁徙率P对其进行调整; 还有调整算子生成, 同样可以通过调整率BAR对其进行影响. 二者可以并行执行, 以便更好地处理收敛性与多样性之间的平衡关系. MBO对君主蝶的迁徙行为的理想假设模型:

(1)种群中所有个体均来自LandP1与LandP2.

(2)为了保持总人口不变, 本文将会对父代与子代进行统一排序, 仅选取排名靠前的个体作为下一代种群.

(3)不对适应值最优的两个个体做任何处理, 自动移到下一代.

2.1 初始化

在搜索空间中随机生成满足种群数量的个体, 依据目标函数计算每个个体的适应度, 并据此进行从优到劣的一次排序.

将种群分为两个子群LandP1、LandP2, 保证种群中的个体只会栖息在两个子群中. 子群一的个体数N1为种群的总个数N×迁徙率P (P=5/12)的整数部分, 即 $N1 = {\rm{ }}ceil\left( {P{\rm{ }} \times {\rm{ }}N} \right)$ , 子群二的个体数N2为剩下的部分N–N1.

2.2 精英策略

对于每次迭代, 选出种群中适应度最好的两个个体, 将他们替代掉下一次迭代过后的种群中的最差的两个个体.

2.3 迁徙算子

对子群一中的君主蝶第i个体的所有维度, 生成一个随机数r=rand*peri与P比较, 若r ≤ P则子代的第k维由式(1)生成:

$x_{i,k}^{t + 1} = x_{j1,k}^t*a + x_{j2,k}^t*(0.9 - a) + x_{{\rm {best}},k}^t*0.1$

(1)

其中, $x_{i,k}^{t + 1}$ 表示 ${x_i}$ 在t+1时刻的第k维, 表示个体i的位置; rand是[0,1]之间均匀分布的随机数; peri为迁移周期, 算法中设置为1.2; i=1,2,···,N1; k=1,2,···,d; t为当前迭代数; j1为在子群一中随机一个个体; j2为在子群二中随机一个个体; ${x_{\rm {best}}}$ 为当前种群的最优个体的位置; a为[0.5,0.9]之间的随机数. 若r > P则子代的第k维由式(2)生成:

$x_{i,k}^{t + 1} = x_{j2,k}^t*a + x_{j1,k}^t*(0.9 - a) + x_{{\rm {best}},k}^t*0.1$

(2)

在标准MBO中迁徙算子子代生成的公式为取某一个体的维度直接进行赋值, 而本文改为对多个对象进行权重分配, 再赋值.

2.4 调整算子

除了子群一中的迁徙算子对其进行位置更新, 还有对子群二作用的调整算子. 对子群二中的君主蝶第 $ i $ 个体的所有维度, 生成一个随机数r=rand与P比较, 若r ≤ P, 则子代的第k维由式(3)生成:

$x_{i,k}^{t + 1} = x_{{\rm {best}},k}^t$

(3)

若r > p则子代的第k维由式(4)生成:

$x_{i,k}^{t + 1} = x_{j2,k}^t$

(4)

在此条件下, 若r > BAR, 则该个体由式(5)进行调整:

$x_{i,k}^{t + 1} = x_{i,k}^{t + 1} + \alpha \times (d{x_k} - 0.5)$

(5)

其中, BAR为调整率, 算法中设置BAR=P, $\alpha $ 为权重因子, $dx$ 为君主蝶i的步长. $\alpha $ 和 $dx$ 分别由式(6)和式(7)来计算:

$\alpha = {S_{\max }}/{t^2}$

(6)

$dx = Levy(x_i^t)$

(7)

其中, ${S_{\max }}$ 为君主蝶的最大步长, t为当前迭代数.

3 Logistic混沌映射君主蝶优化算法 3.1 Logistic混沌映射

一个系统如果在其进化的过程中对初始的状态非常敏感, 则这个系统就是混沌系统, 且这个过程具有确定性、类似随机性、非周期性. 混沌序列的生成方法主要采用以下几类混沌映射^[11]: Logistic映射、Tent映射、Henon映射、Lorenz映射、逐段线性混沌映射等. 由于Logistic映射从数学的形式上看是个相对简单的映射方法, 经验实验表明其混沌系统具有良好的安全性, 所以经常被用作设计混沌流密码系统, 本文即选用Logistic对种群中的最优个体进行混沌映射.

标准的MBO在解决高维问题时易陷入局部最优, 这里引入方差 ${\sigma ^2}$ 的定义对君主蝶的种群是否陷入局部最优进行判断:

${\sigma ^2} = \sum\limits_{i = 1}^N {\left( {\dfrac{{{f_t} - {f_{\rm {avg}}}}}{f}} \right)} $

(8)

其中, N为君主蝶中的种群个体总数, ${f_{\rm {avg}}}$ 为种群整体适应度的平均值, ${f_t}$ 为个体t的适应度. $f$ 用来限制 ${\sigma ^2}$ 的大小, 其取值方式为:

$f = \left\{ \begin{array}{l} \max \{ \left| {{f_t} - {f_{\rm {avg}}}} \right|\} ,\;\max \{ \left| {{f_t} - {f_{\rm {avg}}}} \right|\} > 1\\ 1,\;\max \{ \left| {{f_t} - {f_{\rm {avg}}}} \right|\} \le 1 \end{array} \right.$

若相邻的两次 ${\sigma ^2}$ 相差小于一个阈值(本文定为 $ {10}^{-6} $ ), 则表示算法在迭代过程中陷入了局部最优, 此时进入Logistic混沌映射阶段对当前种群中适应度最优的个体的位置进行扰动, 由式(9)生成扰动个体:

${{\textit{z}}_i}(t + 1) = \mu {{\textit{z}}_i}(t)(1 - {{\textit{z}}_i}(t))$

(9)

其中, ${{\textit{z}}_i} \in \left[ {0,1} \right]$ 是第i个混沌变量, ${{\textit{z}}_i}(t)$ 是 ${{\textit{z}}_i}$ 经过t次迭代后产生的. 图1为当君主蝶中的个体 ${x_i}$ 一定时, 对 $\;\mu $ 不同的取值, ${{\textit{z}}_i}$ 可能得到的值. $\mu \in \left[ {0,4} \right]$ , 由图1可以看出当 $3.57 < \mu \le 4$ 时, 整个系统处于混沌状态, 因此需要选取的 $\;\mu $ 应该越接近4越好, 但是考虑到对于进行混沌映射时不同的情况可能需要不同的 $\;\mu $ 值, 为了尽可能地取到更多的 $\;\mu $ , 因此本文在每次进入混沌映射阶段时取 $\;\mu $ 为一个[0,4]中均匀分布的随机值.

由于当 ${{\textit{z}}_i} \in [0,1]$ 且 ${{\textit{z}}_i} \notin \{ 0.25,0.50,0.75\} $ 时将产生混沌现象, 所以0.25, 0.50, 0.75为 ${{\textit{z}}_i}$ 定义域中的断点, 映射时应当不处理这些值. 对于君主蝶群体中的个体 ${x_i} \in [{a_i},{b_i}]$ 由式(10)映射到 ${{\textit{z}}_i} \in [0,1]$ :

${{\textit{z}}_i} = \dfrac{{{x_i} - {a_i}}}{{{b_i} - {a_i}}}$

(10)

而 $ {{\textit{z}}}_{i} $ 由式(11)映射回 $ {x}_{i} $ :

${x_i} = {a_i} + {{\textit{z}}_i}({b_i} - {a_i})$

(11)

算法对适应度最优的个体一次映射生成20个个体.

3.2 LCMMBO算法

众所周知, 群智能算法需要平衡其收敛性与多样性^[12], 本文通过改进的迁徙算子遗传方程增加其全局搜索能力, 通过混沌映射增加其局部搜索能力, 进而带动种群朝全局最优的位置进化^[13]. LCMMBO算法的流程如下:

步骤1. 在目标空间随机初始化50个个体, 初始化设置t=1, MaxFEs=500, P=5/12, BAR=5/12, peri=1.2, N1, N2, ${S_{\max }}$ =1. 计算种群中每个个体的适应值.

步骤2. 把君主蝶种群根据迁徙率P分成两个子群LandP1, LandP2, 个体数分别为N1, N2.

步骤3. 精英策略: 取当前种群中最优的两个体放入临时序列, 并在本次迭代结束的时候替换掉种群中最差的两个个体.

步骤4. 将迁徙算子作用于LandP1.

步骤5. 将迁徙算子作用于LandP2.

步骤6. 合并两个子群为一个种群, 并根据公式(8)计算本次迭代中种群的方差 ${\sigma ^2}$ , 从t>2时开始比较相邻两次的方差, 如果小于 $ {10}^{-6} $ 则表示陷入局部最优, 进入步骤7, 否则进入步骤8.

步骤7. 取出当前种群中适应度最优个体的位置, 对其进行混沌映射, 生成20个个体, 计算它们的适应值. 若最优个体比种群中的最优个体的适应值更好, 那就把种群中的最优个体替换, 否则不变.

步骤8. 判断是否满足迭代终止条件, 若不满足则 $t = t + 1$ , 进入步骤2.

4 仿真实验 4.1 Benchmark测试函数

本文将LCMMBO算法与MBO算法、CABC算法进行优化性能对比分析. 随机抽取10个常见的用来测试算法性能的基准函数用于测试以上算法的优化性能, 本文所有用于测试的基准函数的全局最小值均为0, 且n=50.

(1) Ackley函数

$\begin{array}{l} {f_1}(x) = - 20\exp \left( { - \dfrac{1}{5}\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} } } \right) - \exp \left[ {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\cos \left( {2\pi {x_i}} \right)} } \right] \\ \qquad\quad + 20 + \exp \left( 1 \right), - 30 \le {x_i} \le 30 \\ \end{array} $

Ackley函数的特点是外部区域几乎平坦, 中央有一个大孔, 该函数容易使算法陷入许多局部最优.

(2) Dixon-Price函数

${f_2}(x) = {\left( {{x_1} - 1} \right)^2} + \sum\limits_{i = 2}^n {i{{\left( {2x_i^2 - {x_{i - 1}}} \right)}^2}} , - 10 \le {x_i} \le 10$

该函数是一个谷型函数, 在 ${x_i} = {2^{ - \frac{{{2^i} - 2}}{{{2^i}}}}},i = 1,\cdots,n$ 时取得全局最小值0.

(3) Griewank函数

${f_3}(x) = \dfrac{1}{{4000}}\sum\limits_{i = 1}^n {{x^2}} - \prod\limits_{i = 1}^n {\cos \left( {\dfrac{{{x_i}}}{{\sqrt i }}} \right) + 1} , - 600 \le {x_i} \le 600$

该函数具有许多分布规则的复杂的局部最小值在其中, 在点(0,···,0)处取得全局最小值0.

(4) Levy函数

$\begin{array}{l} {f_4}(x) = {\sin ^2}\left( {\pi {w_1}} \right) + \displaystyle\sum\limits_{i = 1}^{n - 1} {{{\left( {{w_i} - 1} \right)}^2}\left[ {1 + 10{{\sin }^2}\left( {\pi {w_i} + 1} \right)} \right]} \\ + {\left( {{w_n} - 1} \right)^2}\left[ {1 + {{\sin }^2}\left( {2\pi {w_n}} \right)} \right],{w_i} \!= \!1 + \dfrac{{{x_i} - 1}}{4}, - 10 \le {x_i} \le 10 \\ \end{array} $

该函数为多峰函数, 在点(1,···,1)处取得全局最小值0.

(5) Rastrigin函数

${f_5}(x) = 10n + \sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right)} \right]} , - 5.12 \le {x_i} \le 5.12$

该函数是个典型的测试函数, 是个高度多峰但位置却均匀分布的函数, 在点(0,···,0)取得全局最小值0.

(6) Rosenbrock函数

${f_6}(x) = \sum\limits_{i = 1}^{n - 1} {\left[ {100{{({x_{i + 1}} - x_i^2)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right]} , - 5 \le {x_i} \le 10$

该函数时单峰函数, 全局最小值位于狭窄的抛物线型的山谷中, 很难收敛到最小, 在点(1,···,1)处取得全局最小值0.

(7) Rotated Hyper-Ellipsoid函数

${f_7}(x) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^i {x_j^2} } , - 65.536 \le {x_i} \le 65.536$

该函数为一个单峰的旋转的椭球, 再点(0,···,0)处取得全局最小值0.

(8) Salomo函数

${f_8}(x) = 1 - \cos \left( {2\pi \sqrt {\sum\limits_{i = 1}^n {x_i^2} } } \right) + 0.1\sqrt {\sum\limits_{i = 1}^n {x_i^2} } , - 100 \le {x_i} \le 100$

该函数为多峰函数, 在(0,···,0)处取得全局最小值0.

(9) Sphere函数

${f_9}(x) = \sum\limits_{i = 1}^n {x_i^2} , - 5.12 \le {x_i} \le 5.12$

该函数为经典单峰测试函数, 在点(0,···,0)处取得全局最小值0.

(10) Wavy函数

${f_{10}}(x) = - \dfrac{1}{n}\sum\limits_{i = 1}^n {\cos \left( {10{x_i}} \right){e^{ - \frac{{x_i^2}}{2}}} + 1} , - \pi \le {x_i} \le \pi $

该函数是个经典多峰函数, 在点(0,···,0)处取得最小值0.

目前的群智能算法已经在低维的优化问题上表现出良好的性能, 但是对于高维问题一些算法的求解效果会出现明显下滑^[14]. 现实中的问题往往具有多个影响因素, 也就意味着我们对高维优化问题的求解方法不能忽视, 这也是本文研究的目标之一.

4.2 模拟实验

初始化参数设置: 3种算法的种群个体数都为50、最大迭代次数为50、每个个体维度50, 其他参数与原文保持一致.

对于10个Benchmark基准函数, 每个算法独立进行30次实验, 并记录其30次实验中的最优解, 最劣解, 平均解和标准差等测试结果. 本文选择的这些评价指标能一定程度上的反应新算法LCMMBO在标准MBO算法的鲁棒性以及全局搜索能力上的优化.

表1为3种算法在10个优化问题上独立运行30次的具体实验结果.

为了更直观的体现LCMMBO算法相较于MBO、CABC的优越性, 本文将作LCMMBO、MBO、CABC三种算法分别在10个基准函数上独立运行30次的迭代次数与平均适应值的曲线仿真图2至图11作为参考.

4.3 实验结果分析

在表1中, 从最优值这个评价指标上看, LCMMBO算法除了在 ${f_3}$ 上得到了明显优于MBO、CABC两个算法的最优值, 在其余的基准函数上LCMMBO算法并没有表现出优异的性能. 从最差值、平均值与标准差上看, 由于LCMMBO算法跳出局部最优的优异, 所以在这3个评价指标上可以清楚地看到新算法在鲁棒性上的优化. 例如: 最差在函数 ${f_1}$ 、 ${f_8}$ 上平均值相比MBO算法优化了大约10倍; 最好在 ${f_2}$ 、 ${f_4}$ 上平均值相比MBO算法优化了10⁶倍.

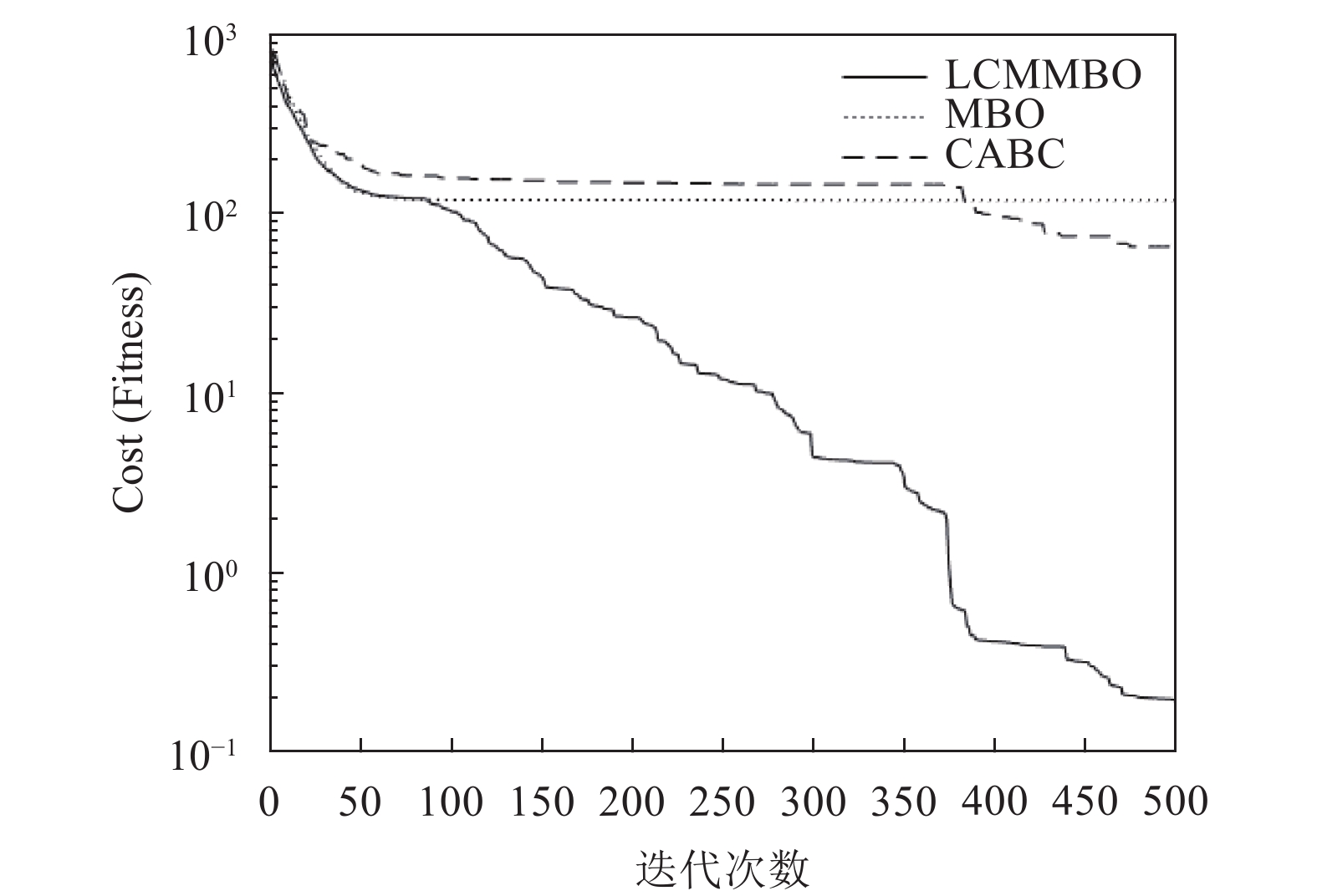
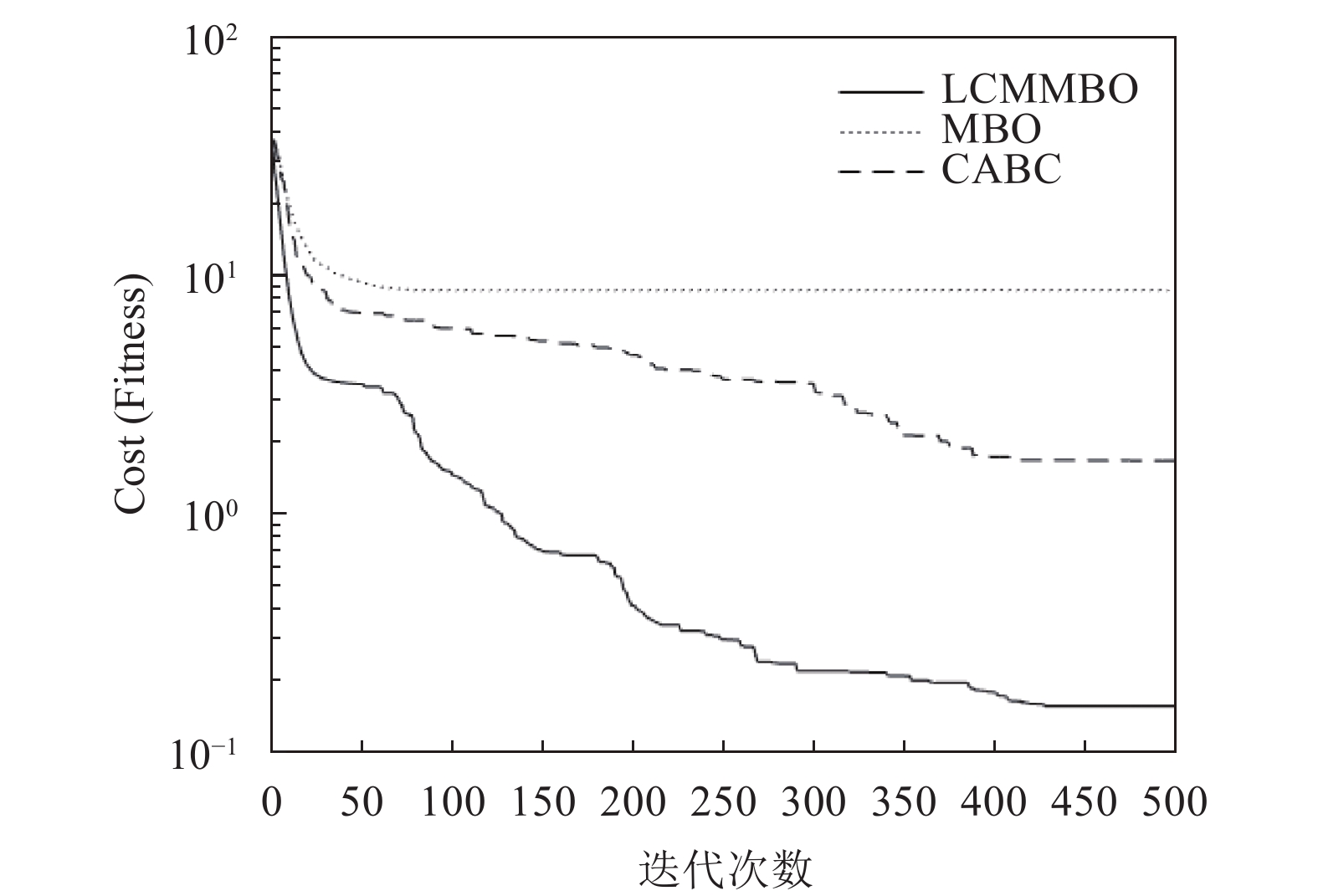
从图2至图11中可以看到LCMMBO算法的收敛曲线具有明显的下降趋势, 相比MBO、CABC更接近目标函数的理论最优值, 而从图2、图7、图11中可以看出MBO和CABC的进化曲线几乎没有下降的趋势, 从曲线的下降速度看, 除了图6、图11以外, LCMMBO的下降速度也要优于二者. 这说明LCMMBO由于具有更好的全局探索及局部搜索平衡能力, 因此寻优性能明显优于MBO和CABC; LCMMBO比MBO和CABC具有更快的全局收敛速度, 表现出更好的收敛性; LCMMBO比MBO和CABC具有更好的全局搜索能力.

图2至图11都非常清楚地显示了MBO在处理高维问题时易陷入局部最优的问题; CABC虽然对陷入局部最优问题做了一些处置, 但效果显然没有LCMMBO明显. 另外, 从图3、图6中可以看到CABC在资源的利用率上不如LCMMBO, 在陷入局部最优时CABC需要更多的迭代实现跳出局部最优的行为.

综上所述, 新算法LCMMBO的稳定性比MBO和CABC更优; LCMMBO相较于MBO和CABC具有更好的收敛性; LCMMBO相较于MBO和CABC具有更强的局部搜索能力以及全局搜索能力; LCMMBO跳出局部最优的能力比MBO和CABC好.

5 结语

本文针对标准MBO存在的迁徙算子影响源过少, 以及处理高维度问题时容易陷入局部最优, 全局搜索能力差, 提出一种新的基于Logistic混沌映射的MBO算法, 并改进了其迁徙算子遗传方程. 通过对10个Benchmark基准测试函数的模拟实验, 说明了新算法LCMMBO在解决高维函数优化问题时相比较标准MBO, CABC算法具有更优的鲁棒性、更快的全局收敛速度、更强的局部搜索能力和全局搜索能力、更好的跳出局部最优的能力; 说明了本文提出的改进方案是有效且可实施的. 在未来的研究中还应该注意一些可能进行优化的地方, 比如: 参数对于群智能优化算法的性能有很大的影响, 最佳的参数设置应该经过理论分析或经验实验决定等.