我国虽然是当今世界上拥有制造资源最丰富的国家, 但是资源的有效使用效率低造成了资源的极大浪费, 不利于我国制造业的发展. 随着云计算、物联网、虚拟化等技术的出现, 云制造的概念被一些学者提出. 云制造是一种基于网络的, 面向服务的智慧化制造新模式手段, 它融合发展了现有信息化制造技术与云计算、物联网、服务计算、智能科学等新兴信息技术, 将各类制造资源和制造能力虚拟化、服务化, 构成制造资源和制造能力的云服务池, 进行统一的、集中的优化管理和经营, 使得用户只要通过云端就可以随时随地按需获取制造资源和服务能力, 进而智慧的完成其制造全生命周期的各类活动. 由于对制造资源和制造能力进行了统一的管理分配, 使得资源的利用率大大提高, 并且不同资源调度方案对不同资源的使用情况也不同, 因此对资源的合理调度成为研究的热点. 由于云平台任务数量众多, 精确解的获取非常困难, 因此云平台需要将某一时刻到达的任务集中在一起, 通过合适的调度算法确定其优先顺序获得近似解, 以此解决云制造调度问题. 由于具体的任务执行过程的不确定性, 如: 紧急任务的到达、由于机器故障等因素导致服务暂停、任务的取消, 这些因素会引起云制造系统的重调度, 本文旨在解决任务动态调度过程中紧急任务的到达和服务暂停问题.
目前, 求解传统车间调度的方法有精确算法和近似算法. 毛志慧等[1]提出一种文化基因非支配排序粒子群算法, 旨在优化产品的合格率、缩短生产周期、减少机器的空转时间. 杜兆龙等[2]以粒子群算法为基础, 引入变邻域搜索方式, 提出基于解空间距离聚类和变邻域搜索的粒子群算法. Ding等[3]提出了一种改进的粒子群算法来解决柔性作业车间调度问题, 并通过改进编解码方案、粒子之间的通信机制和候选操作机器的交替规则来获得有益的解决方案, 并对编译码方案进行了创新, 提出了一种新颖的链式编码方案和相应的有效译码方案. Chen等[4]设计一种基于强化学习对关键参数进行智能调整的自学习遗传算法.
与传统车间调度方法类似, 对云系统任务的调度可以采用遗传算法、粒子群算法等元启发式算法来获取最优解. 李云龙等[5]针对云制造环境下柔性作业车间调度产生的离散型加工设备的空闲时间利用及其冲突问题, 提出了一种基于混合遗传算法的云制造环境下柔性作业车间调度方案, 以最小惩罚总成本为目标,采用了遗传变邻域混合算法求解云任务工件最优调度顺序. 王时龙等[6]考虑服务需求者间存在的利益冲突及重要的服务评价指标,以每个任务的执行制造路径为博弈策略,将有限资源的多任务调度问题转变为多个静态非合作博弈问题. 郑楚红等[7]针对云制造环境下的多目标任务调度问题, 改进非支配排序生物地理优化算法, 通过基于权重均匀分配策略定义的用户偏好度来评估制造任务调度方案的质量, 并设计梯形迁移率计算模型扩大其搜索邻域, 避免陷入局部最优解. Xiao等[8]为解决云制造的多任务调度问题, 提出了一种基于博弈理论的云制造多任务调度模型, 并利用一种嵌入三种改进的基于生物地理学的扩展优化算法来求解相应模型. Zhou等[9]针对不同任务的调度问题, 根据子任务有向图生成候选服务集, 利用一种改进的遗传算法来寻找任务调度的最优解. Zhang等[10]针对任务随机到达的动态云制造环境中的任务调度问题, 提出了一种事件触发的动态任务调度方法, 事件触发策略的设计考虑了新任务的到来和子任务序列中第一或中间子任务的完成, 结合候选服务的服务时间、物流时间和最早可用的时间, 为被触发的子任务选择最优服务.
由上述文献可知, 在云环境下的任务调度系统中, 很少涉及动态任务调度问题, 为了更好地解决云环境下的调度问题, 并考虑到云环境下任务的规模很大, 遗传算法因其可以在较为合理的计算时间内迅速求得较为理想的满意解, 适合用于求解较大规模的调度问题, 因此本文以任务的最大完成时间为优化目标, 提出了一种改进的遗传算法来解决由于紧急任务到达、服务故障导致的重调度问题.
1 问题描述在云制造系统中, 各种制造资源被封装到制造服务中, 资源服务以不同的形式提供各种制造能力. 由于在大部分情况下, 任务请求复杂且众多, 为了调度执行这些任务, 将其分解成一组具有优先关系的子任务, 且子任务之间有相互约束关系.
N个任务由P×S个服务执行, 其中P和S分别代表云平台上供应商的数量和每个供应商提供的服务数. 每个任务由不同的子任务组成, 并且每个子任务对应的任务类型不同. 根据任务类型的不同, 选择不同的服务来执行任务, 每个供应商所提供的服务可以执行一个或多个不同类型的子任务. 本文所考虑的调度问题包括任务的排序、在不违反优先约束的情况下从每个任务分解出的子任务的排序以及选择合适的服务来最小化最大完工时间
云制造系统调度问题需要考虑如下约束条件:
(1) 一个服务在同一时间只可执行一个任务;
(2) 一个子任务只可由一个服务执行处理;
(3) 同一任务的子任务存在优先关系, 需要按顺序执行;
(4)任务不可被抢占, 任务在执行过程中不能被中断;
(5) 材料资源充足, 每个任务所需的资源不会短缺;
针对带有紧急任务和服务暂停的云制造调度, 目标是找到一个最优的子任务序列和服务序列, 使得最大完成时间最小化.
2 重调度云环境下的任务在执行过程中会遇到许多特殊情况, 这些特殊情况会中断正在执行的任务, 当特殊情况到达时, 需要统计任务的完成情况: 已经完成的任务、正在加工的任务、还未执行的任务, 再根据具体的情况对这些任务进行重新调度. 本文对云制造环境下的动态调度研究考虑了两种常见的中断类型: “紧急任务到达”和“服务暂停”, 并给出了一种与邻域搜索相结合的改进遗传算法, 对紧急任务的到达和服务暂停问题得到了很好的解决.
2.1 紧急任务到达云环境下的任务来自于不同的客户的不同需求, 云平台根据相应规则将客户分为高优先级客户和普通优先级客户, 高优先级客户具有优先执行任务的权力. 在实际的任务执行过程中订单的优先级都是相同的, 当优先级高的客户在云平台上发布任务需求时, 该任务就会作为紧急订单加入到系统中, 云制造调度系统在这时会产生一个中断, 并统计系统中任务的完成情况, 将还未完成的任务与紧急任务作为新的需要重新调度的任务输入到云制造调度系统中, 通过改进的遗传算法调度产生最优解. 在调度过程中优先考虑完成紧急任务, 即当紧急任务与普通任务选择同一个服务执行时, 紧急任务优先使用该服务.
若在某时刻云平台的一个超级会员客户产生了一个紧急任务, 此时需要统计在该时刻还未完成的任务, 并将紧急任务作为优先执行任务进行重调度, 各个供应商根据调度产生的最优任务序列完成相应任务.
2.2 服务暂停在传统的柔性作业车间调度系统中, 工件在机器上加工, 机器会因为零件老化, 部件磨损等情况导致机器故障, 因此在该机器上加工的工件需要选择其他机器进行加工. 类似于传统柔性作业车间调度问题, 在实际的云环境生产制造过程中, 机器故障、资源紧缺等因素会导致某个服务暂停使用, 需要使用该服务的任务需要选择其他服务来执行, 从而影响任务的完成时间. 当服务无法使用时, 服务只能在恢复之后才能重新执行任务, 因此需要在该时刻重新统计还未完成的任务, 并对这些任务重新选择供应商和服务操作. 云制造系统根据改进遗传算法对这些任务进行迭代寻优, 产生最优调度任务序列, 获取最小的最大完成时间.
3 改进遗传算法遗传算法(Genetic Algorithm, GA)因其优越的性能和较强的通用性, 被认为是求解实际组合优化问题最典型的基于种群的优化算法. 本文提出一种改进的遗传算法用于解决带有紧急任务和服务暂停的云制造调度问题. 改进遗传算法在传统遗传算法的基础上结合了邻域搜索和模拟退火算法, 多样的邻域结构保证在进行全局搜索的过程中陷入局部最优.
传统的遗传算法包含初始化、适应度计算、选择交叉、变异操作, 本文在以遗传算法为基本框架, 提出了一种改进的遗传算法, 该算法包含云制造任务编码、轮盘赌选择、启发式规则交叉、多操作邻域搜索、两点变异, 具体的实现方式如下所示:
3.1 编码方式种群中每一个解包含两个部分, 任务次序部分和服务选择部分. 例如: [2 2 3 1 3 1 1 2]和{[6 4 5 2 1 3 2 6], [1 2 1 3 1 2 2 4]}其中第一个向量的第一个“2”表示第2个订单的第1个子任务, 第二“2”表示第2个订单的第2个子任务, 第二个向量表示每个子任务所对应的供应商及其服务, 比如表示第2个订单的第1个子任务是由供应商6的第一个服务来完成的.
3.2 遗传因子选择、交叉、变异是遗传算法不可缺少的操作, 对获取近似解起到至关重要的作用.
选择: 以轮盘赌的方式选择, 步骤如下:
(1)计算种群中每个个体的适应度值.
(2)计算每个个体遗传到下一代群体的概率.
| $ p\left({x}_{i}\right)=\frac{f\left({x}_{i}\right)}{\displaystyle\sum _{j=1}^{N}f\left({x}_{j}\right)} $ | (1) |
(3)计算个体的累计概率.
(4)随机生成0–1之间的小数, 并根据该数选择相应的个体.
启发式规则交叉: 为了增加种群的多样性, 本文对遗传算法进行改进, 并提出一种启发式规则的交叉方法, 该交叉方法是在一定的数据引导下对两个个体进行交叉操作, 实验结果表明, 该交叉方法优于传统的单点交叉、多点交叉、PMX交叉如图1所示, 具体操作方法如下.

|
图 1 交叉操作 |
(1)生成一个以任务数为大小的向量R, R中的数是0–1之间的随机数, 并随机生成一个0–1之间的数pt.
(2)根据R中小于pt的数对应选择父代1中的任务, 并将其复制到子代中.
(3)选择父代2中大于pt的数对应的任务复制到子代中, 当对应的位置有值时, 不予改变.
(4) 选择父代1中大于pt的数对应的任务复制到子代中, 当对应的位置有值时, 不予改变, 并且确保解的可行性.
(5)统计剩余的子任务, 并随机选择子代中的空余位置, 对子代进行补全.
以图1为例, 根据随机产生的矩阵
变异: 本文采用交换子任务的位置实现变异操作, 使遗传算法具有局部的随机搜索能力.
3.3 邻域搜索遗传算法虽然能够快速的找到近似解, 但是容易陷入局部最优, 这会使得所搜索到的解的结果不好, 本文提出的改进的遗传算法引入了邻域搜索, 旨在打破传统遗传算法陷入局部最优的缺点. 本文所提出的改进遗传算法将邻域操作与模拟退火算法相结合, 在邻域搜索的过程中, 以一定的概率接受差解, 使得遗传算法不会过早的收敛于一个局部值. 具体的邻域操作如下所示:
(1)交换: 随机选择个体的两个位置, 并将相应位置上的任务进行交换.
(2)插入: 随机选择个体中一个位置, 并将该位置上的任务随机插入其他位置上.
(3)交换两次: 进行两次操作(1).
(4)插入两次: 进行两次操作(2).
(5)翻转: 选择个体中的一段基因, 进行翻转.
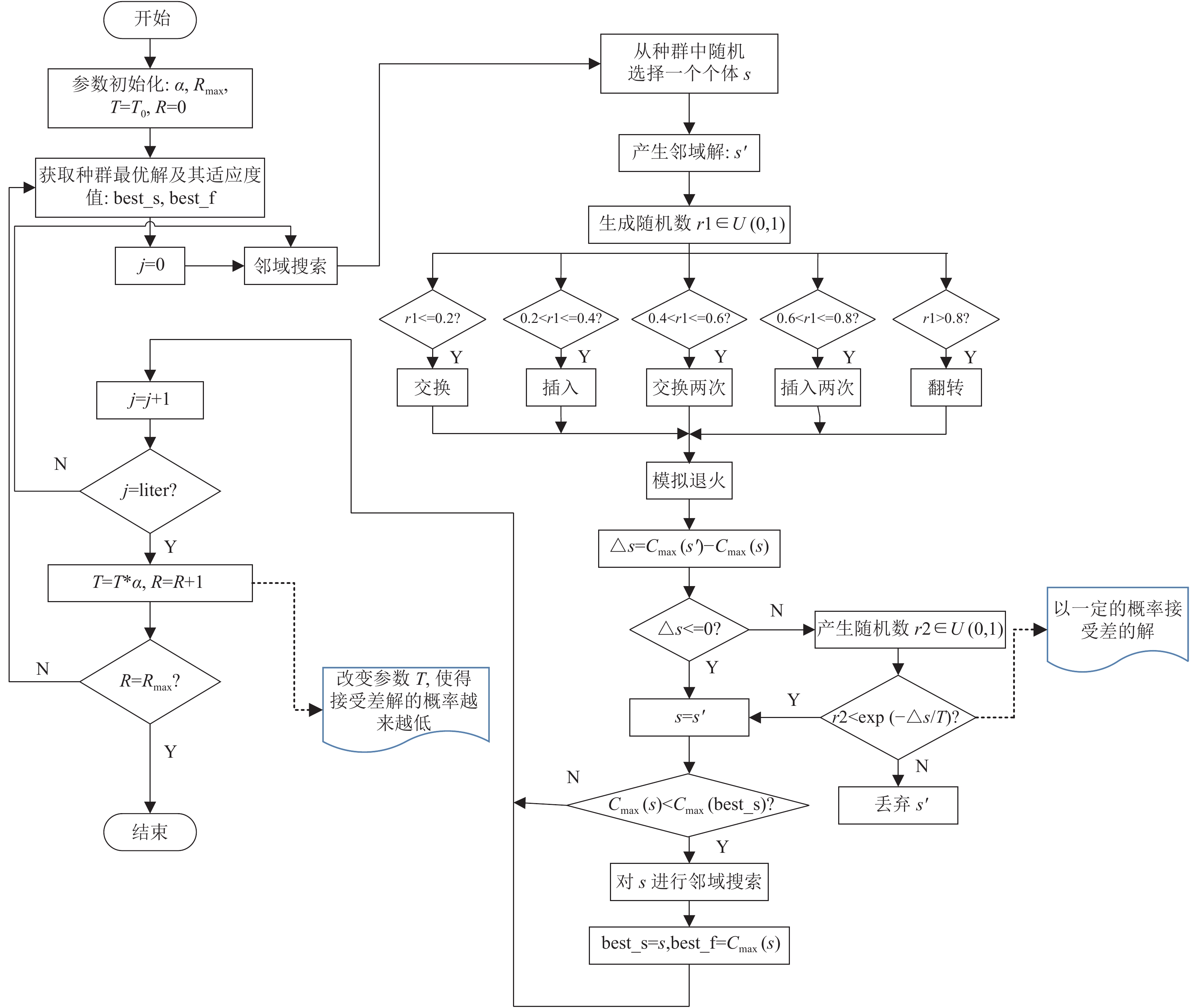
在图2中, 邻域搜索步骤如下:
(1)对参数进行初始化: 其中α为温度衰减因子,
(2)获取种群的最优解及其适应度值;
(3)从种群中随机选择一个个体
(4)判断是否完成相应次数的邻域搜索, 若未达到, 返回第(3)步, 若达到执行第(5)步;
(5)更新温度, 增加迭代次数, 判断是否达到迭代最大值, 若达到则退出, 反之则返回第(2)步.
3.4 改进遗传算法本文所提出的改进遗传算法用于解决云环境下的紧急任务到达和服务故障问题, 具体实现如下:
(1) 统计中断点的待加工任务;
(2) 根据待加工任务进行编码, 产生初始种群;
(3)执行选择、交叉、变异操作, 更新种群;
(4)邻域搜索, 避免陷入局部最优, 获取最优解;
(5)迭代寻优, 产生最优加工序列.
本文对遗传算法的交叉操作因子做了具体改进, 启发式规则下的交叉操作使得种群的解更加丰富多样, 同时降低对种群有效模式的破坏概率. 除此之外, 引入邻域搜索, 扩大了解的搜索范围, 弥补了遗传算法容易陷入局部最优的缺点, 提高了解的质量, 很好的解决了云环境下的动态调度问题.
|
图 2 邻域搜索 |
4 实验结果 4.1 实验数据
表1给出了不同供应商之间的运输时间, 当同一个任务的不同子任务使用不同供应商的服务时, 在求最大完成时间时需要考虑子任务之间的运输时间, 其中0代表起始点, 起始点与不同供应商之间也存在运输时间, 如: 起始点为存储仓库, 客户所需要的任务最终需要运输到此地保存.
在云制造调度的文献中很少考虑由于紧急订单的到达、服务暂停所导致的重调度问题, 所以文献中没有包含所有特征的基准实例进行直接比较, 因此实验数据是参照文献[11]中的数据生成方法随机生成的. 本文数据根据任务和服务数量的不同分为不同的规模, 表2给出了任务类型为6种, 3×3规模的供应商和服务情况下3个任务的数据信息. 该数据包含了每个子任务对应的任务类型和选择的供应商、服务、加工时间, 一种类型的任务可选择不同服务. 供应商、服务和加工时间一一对应.
该数据是还未发生重调度时的数据, 在由紧急任务到达、服务故障引起中断时, 此时需要统计还未完成的任务, 若在中断点之后还未执行的任务为“13”、“23”、“24”、“34”则在重调度时只需将这些任务重新调度.
| 表 1 供应商之间的运输时间 |
| 表 2 任务数据信息 |
4.2 实验结果
在本文中, 不同规模的问题调度产生的最大完成时间如表3所示, 该表包含了正常调度结果和紧急任务以及服务暂停所导致的重调度结果. O、J、T、P、S、H分别代表任务序号、任务数、总子任务数、供应商数、服务数、子任务类型数.
| 表 3 实验结果 |
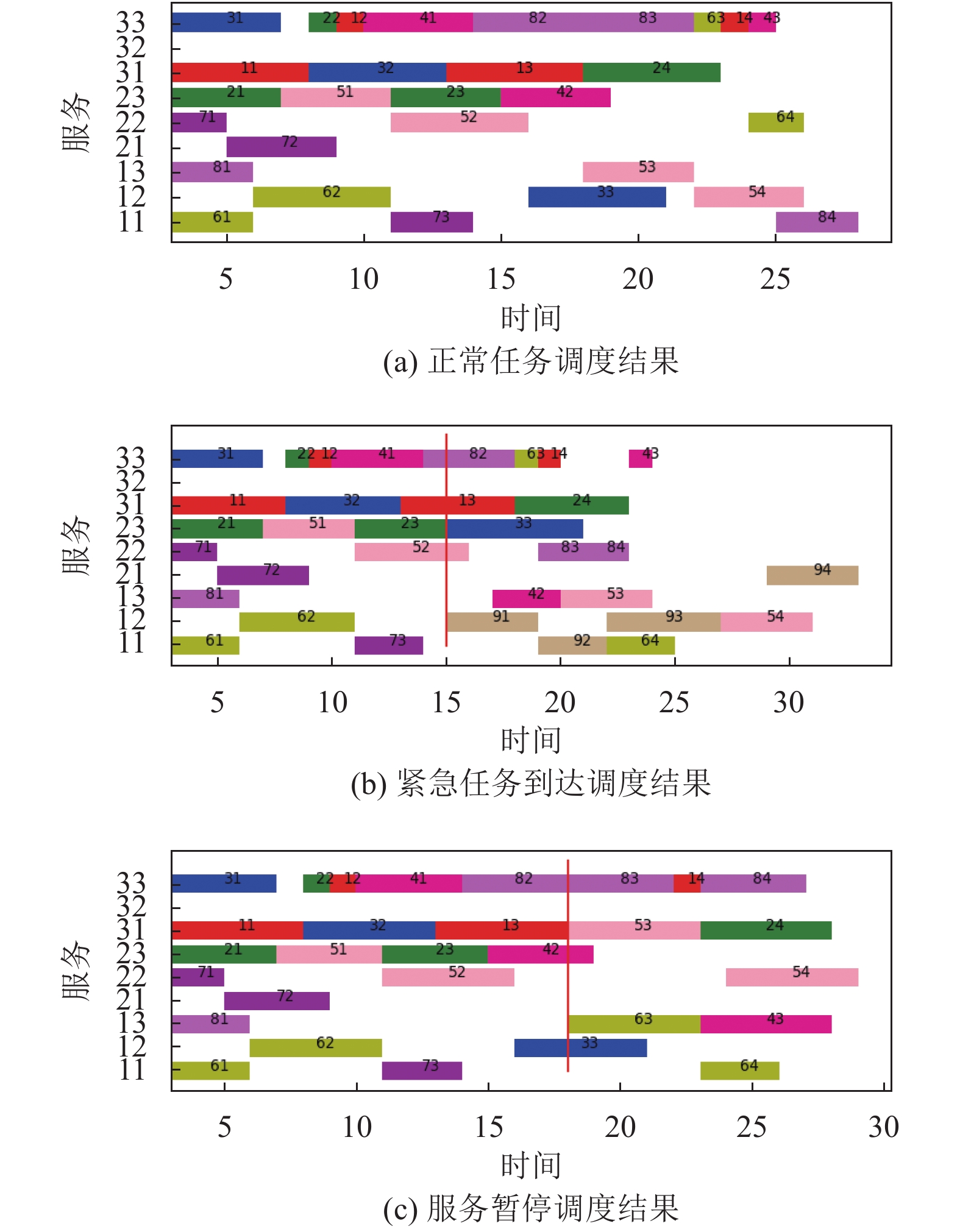
在实例6中, 有29个子任务由9个服务执行, 这些子任务一共有6种类型, 调度的最大完成时间是28, 在执行时间为15时, 到达一个紧急任务, 重调度之后的最大完成时间是33. 若没有紧急任务到达, 且在执行时间为18时发生, 第一个供应商的第二个服务无法使用, 重调度之后的最大完成时间是29.
实例6的实验结果甘特图如图3所示, 该图包含3个子图: 无特殊情况的调度结果图3(a)、在时间为15时由于紧急任务9的插入引起的重调度结果图3(b)、在时间为18时由于第一个供应商的第二个服务暂停引起的重调度结果图3(c). 横轴为时间轴, 纵轴为相应的服务, 如: “11”代表第一个供应商的第一个服务. 红线代表中断时间点, 在图3(b)中, 任务9为紧急任务, 需要优先执行, 如: 任务“54”与任务“93”都需要服务“12”执行, 首先执行任务“93”. 在图3(c)中, 使用故障服务的任务需要重新选择服务, 如: 任务“54”由于服务“12”无法使用, 故重新选择服务“22”.
|
图 3 实验结果 |
本文提出的改进遗传算法与所研究问题的领域没有关系, 它具有随机搜索的能力并可以快速的获取最优解. 相比于其他算法, 本文的算法编码过程简单, 可扩展性很强, 具有良好的全局搜索能力, 该算法以遗传算法为基本框架, 与模拟退火算法相结合, 扩展了解的搜索范围, 可以快速地将解空间中的最优解搜索出, 而不会陷入局部最优解的快速下降陷阱, 除此之外, 本算法利用它的内在并行性可以方便地进行分布式计算, 加快求解速度.
5 结论与展望针对云制造环境下的动态调度问题, 提出了一种与邻域搜索相结合的改进遗传算法, 用来解决动态调度过程中由于紧急任务的到达和服务暂停导致的重调度问题, 来获取任务的最大完成时间的最优值. 实验结果表明, 该算法能够有效的得到任务的最佳执行序列解, 很好的解决动态调度问题. 接下来将会对物流运输进行进一步的研究, 使用机器人或车辆对其进行搬运, 通过合理的调度得到最优调度解, 除此之外, 将会尝试优化算法, 最小化最大完成时间.
| [1] |
毛志慧, 王艳, 纪志成. 多目标柔性车间调度的文化基因非支配排序粒子群算法. 计算机系统应用, 2015, 24(10): 155-161. DOI:10.3969/j.issn.1003-3254.2015.10.026 |
| [2] |
杜兆龙, 徐玉斌, 崔志华, 等. 柔性车间调度的解空间距离聚类和变邻域搜索粒子群算法. 计算机系统应用, 2016, 25(12): 143-148. DOI:10.15888/j.cnki.csa.005482 |
| [3] |
Ding HJ, Gu XS. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Computers & Operations Research, 2020, 121: 104951. |
| [4] |
Chen RH, Yang B, Li S, et al. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Computers & Industrial Engineering, 2020, 149: 106778. |
| [5] |
李云龙, 罗国富, 文笑雨, 等. 基于混合遗传算法的云制造环境下柔性作业车间调度方案. 轻工学报, 2020, 35(3): 99-108. DOI:10.12187/2020.03.012 |
| [6] |
舒萧, 王时龙, 康玲, 等. 面向云制造的有限资源多任务调度博弈. 重庆大学学报, 2020, 43(3): 1-11. DOI:10.11835/j.issn.1000-582X.2019.004 |
| [7] |
郑楚红, 彭勇, 徐一鸣, 等. 云制造环境下基于改进NSBBO的任务调度算法. 计算机工程, 2019, 45(10): 26-32. |
| [8] |
Xiao JH, Zhang WY, Zhang S, et al. Game theory-based multi-task scheduling in cloud manufacturing using an extended biogeography-based optimization algorithm. Concurrent Engineering, 2019, 27(4): 314-330. DOI:10.1177/1063293X19882744 |
| [9] |
Zhou LF, Zhang L, Zhao C, et al. Diverse task scheduling for individualized requirements in cloud manufacturing. Enterprise Information Systems, 2018, 12(3): 300-318. DOI:10.1080/17517575.2017.1364428 |
| [10] |
Zhou LF, Zhang L, Sarker BR, et al. An event-triggered dynamic scheduling method for randomly arriving tasks in cloud manufacturing. International Journal of Computer Integrated Manufacturing, 2018, 31(3): 318-333. DOI:10.1080/0951192X.2017.1413252 |
| [11] |
Baykasoğlu A, Madenoğlu FS, Hamzadayı A. Greedy randomized adaptive search for dynamic flexible job-shop scheduling. Journal of Manufacturing Systems, 2020, 56: 425-451. DOI:10.1016/j.jmsy.2020.06.005 |
 2021, Vol. 30
2021, Vol. 30



