稀疏表示的概念由来已久. 1959年, Hubel和Wiesel^[1]在观察哺乳动物主视皮层V1区神经元感受野的反应的实验中发现该区域细胞感受野对视觉信息的记录方法是一种“稀疏表示”. 基于这一发现, Barlow^[2]于1961年提出了一种假说, 思考了对视觉信号进行编码的可能. 1987年Field^[3]根据Hubel和Wiesel的研究结果, 提出将这一稀疏表示的特性应用于视网膜成像的研究中, 在这一思路的指引下, Michison^[4]于1988年通过结合神经领域的特征与稀疏表示的概念将稀疏编码应用于神经领域. 之后, 在1996年, Olshausen和Field^[5]发现对自然图像进行稀疏编码后获得的基函数与细胞感受野的反应特性具有相似的特征, 通过将稀疏性作为正则化项的方式, 对感受野的响应特性进行了模拟, 从而很好地解释了生物学家观察到的初级视皮层的工作机理. 通过进一步对基函数与输出信号维数之间的思考, 二人研究得出了超完备基稀疏编码的概念, 对V1区简单细胞感受野成功建模. 同一时期, LASSO (Least Absolute Shrinkage and Selection Operato)算法^[6]于1996年创造性地提出了将 ${l_0}$ 范数松弛为 ${l_1}$ 范数来求解稀疏表示模型的方法, 开辟了一条求解稀疏表示模型的新思路. 随着求解最小化范数的算法不断优化, 稀疏表示理论开始被广泛地应用于人脸识别、目标追踪、盲源分离等领域.

1 稀疏表示原理

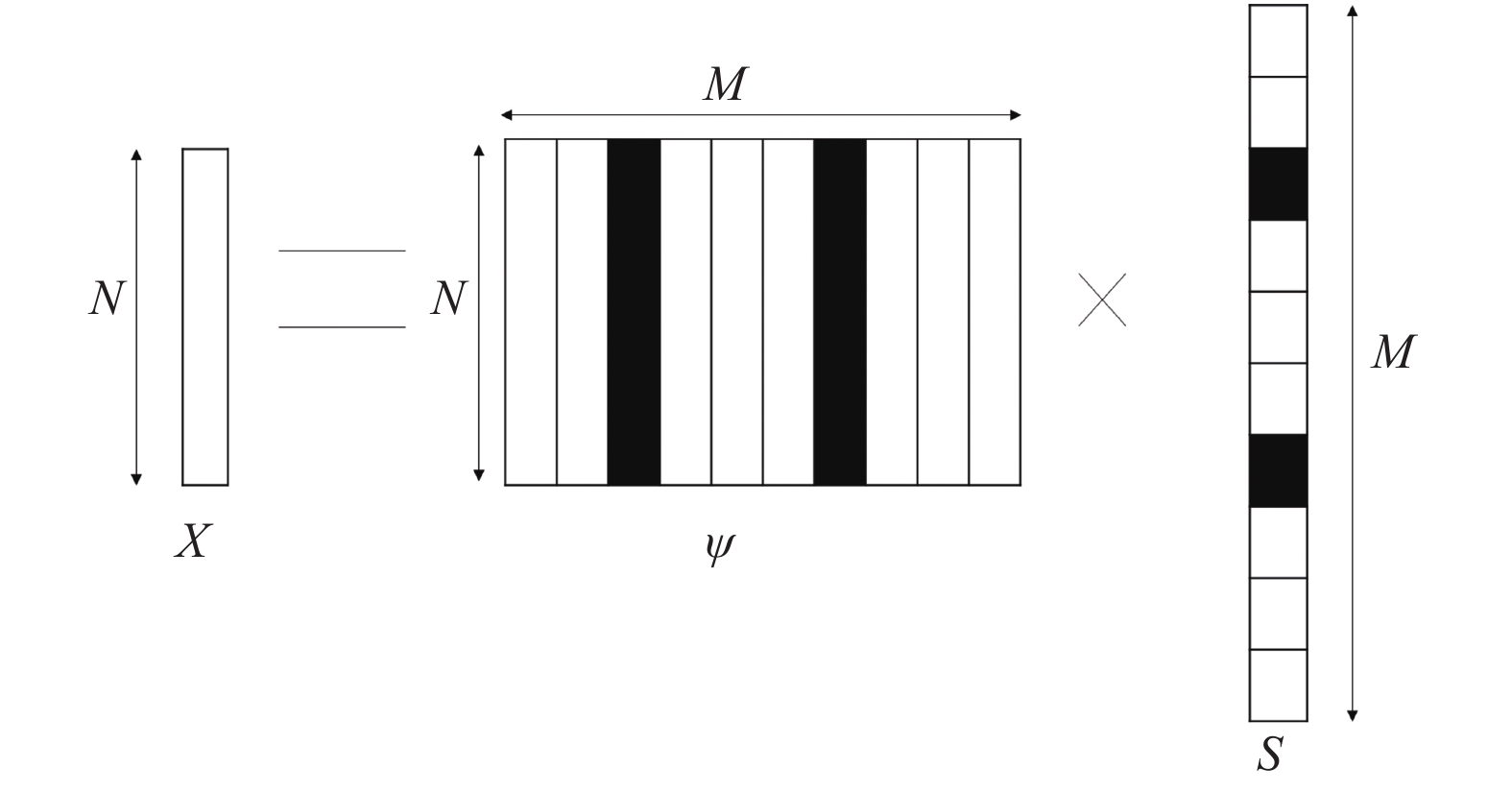
对于一维的离散时间信号 $x$ , 可以用一个 ${{{R}}^{{N}}}$ 空间中的 ${{N}}$ 维列向量来表示. 假设 ${{{R}}^{{N}}}$ 空间内的任何信号都可以通过 ${{N}} \times {{M}}$ 维的基向量组 $\left\{ {{\Psi _i}} \right\}_{i = 1}^{{M}}$ 来线性表示. 此时假设基向量之间都是正交的, 则所有的基向量就构成了一个基矩阵 $\Psi = \left\{ {{\Psi _1}, {\Psi _2}, \cdot \cdot \cdot , {\Psi _{{M}}}} \right\}$ , 这个基矩阵就被称为字典, 信号 $x$ 就可以通过基矩阵表示为以下形式^[7]:

$x = \sum\limits_{i = 1}^M {{s_i}} {\Psi _i}\;\;{\rm {or}}\;\;\;x = \Psi s$

(1)

其中, $s$ 是信号 $x$ 在基矩阵上的投影, 是一个M维的列向量. 如果向量 $s$ 中的非零值数目K远小于向量的维数N, 则认为信号 $s$ 是稀疏的, 当M>N时, $s$ 有无穷多个解, 要得到唯一解需要增加限制条件^[8]. 稀疏表示就是利用这种欠定的情况, 从过完备字典中选取少量原子来表示出原始信号, 即以向量 $s$ 稀疏为约束条件缩小解的范围, 以此来降低信号处理成本, 达到压缩信号的效果. 图1描述了原信号、字典和系数矩阵三者的关系.

向量 $s$ 稀疏的数学定义如下^[9]:

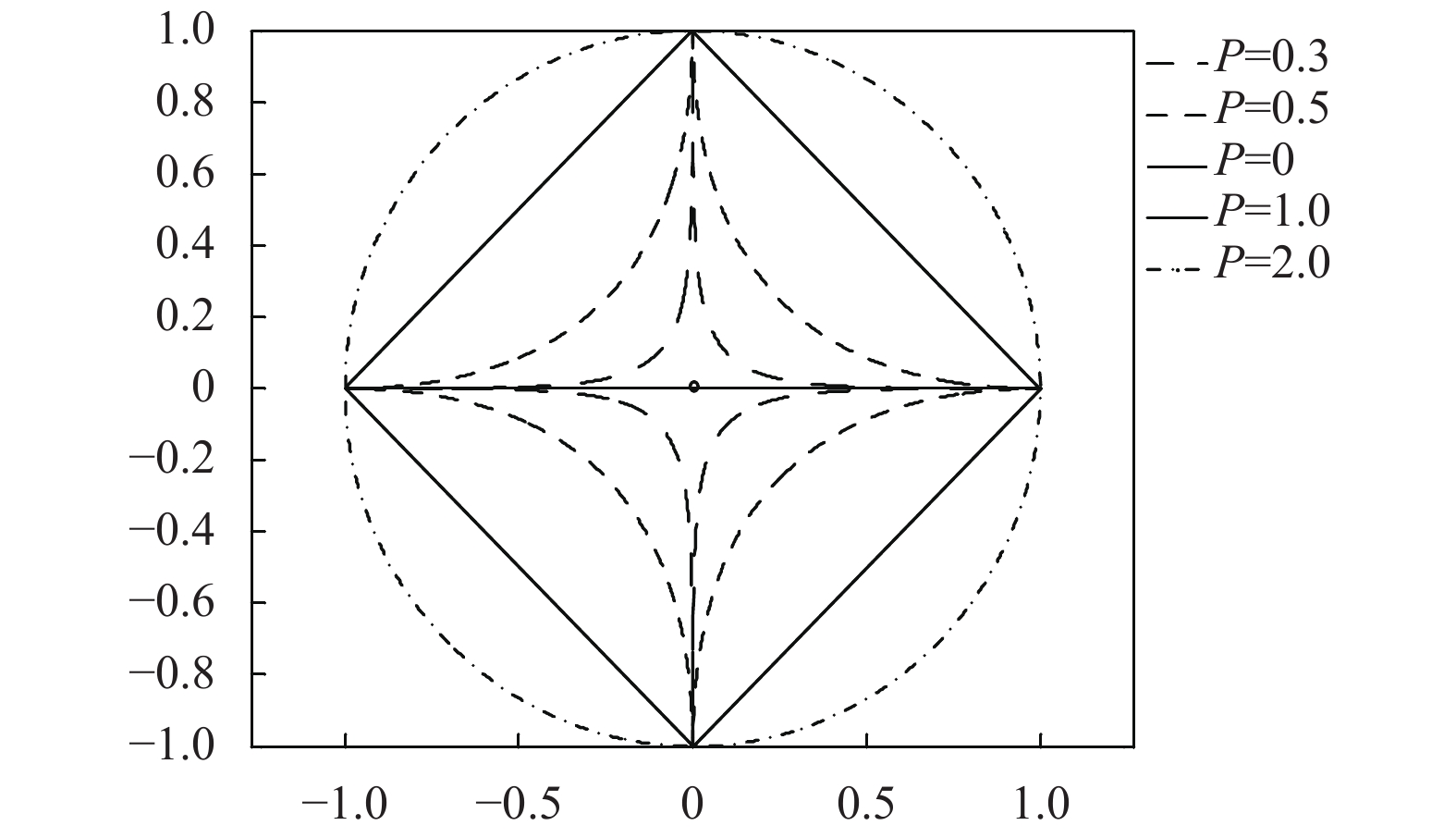
若存在0<P<2和R>0且满足:

$||s|{|_P} = {\left( {\sum\limits_i {|{s_i}{|^p}} } \right)^{\frac{1}{p}}} \le R$

(2)

则认为信号在一定意义上是稀疏的.

同时这一公式也是向量 $s$ 的 ${l_{{P}}}$ 范数定义. 当P为1的时候得到的就是向量的 ${l_1}$ 范数, 意义是向量各个分量元素的绝对值之和; 当P为2的时候得到的就是向量的 ${l_2}$ 范数, 数学意义为根号下各元素的平方和. 图2描述了P为不同值时的 ${l_{{P}}}$ 范数图像.

由此可以将向量 $s$ 稀疏作为求解线性方程组的限制条件, 从而将求解式(1)的问题转化为求解向量的最小 ${l_0}$ 范数的优化问题^[10], 即:

${\rm{\hat s = argmin}}\left\{ {||x - \Psi s||_2^2 + \lambda ||s|{|_0}} \right\}$

(3)

但由于该问题是一个非凸函数求极值的问题, 所以直接求解比较困难^[11], 因而出现了两种求解思路, 一种是通过松弛 ${l_0}$ 范数的方法将非凸问题转换为凸函数再进行优化, 这种方法只能获得近似解; 另一种是采用字典原子匹配的方法, 典型的如下文所述贪心算法. 本文目的即是根据不同求解方式的特点, 对求解算法进行分类, 简要介绍不同算法的原理并整理不同类别算法的发展现状.

2 稀疏表示算法分类

稀疏表示算法根据优化思路可分为贪心算法、约束算法以及其他算法, 其中贪心算法又可分为匹配追踪法、正交匹配追踪算法以及相关衍生算法; 约束算法可分为梯度投影稀疏重构算法、内点法和交替方向法以及其他衍生算法; 其他算法中仍旧包含很多类别, 但由于相关类别所包含算法较少, 就不做进一步划分. 本文主要就前两者的特点, 简单介绍相关原理及其典型算法和发展现状.

2.1 稀疏表示贪心算法

贪心算法的核心思想就是用局部优化来代替全局优化, 提高算法的运算效率. 该类算法都是通过一步一步增加有效列的方式来获得最接近原信号的解. 初始有效集合为空集, 每一步增加的列都要能够最大限度地减少有效集与原信号之间的重构残差, 当这个重构残差小于一个阈值时结束运算. 贪心算法提供了一种求解稀疏表示解的特殊方法^[12].

匹配追踪算法(MP)^[13]是最早的使用贪心策略求解稀疏表示问题近似解的方法. 匹配追踪算法的思想就是通过求内积的方式, 从过完备字典中寻找与输入信号最为匹配的原子, 用初始残差剪掉这一原子后得到下一代残差, 重复这一过程直到残差小于给定的阈值^{[14, 15]}.

匹配追踪算法提供了求解最小化 ${l_0}$ 范数的优化问题的思路, 但其存在一个明显的缺陷, 即在将信号残差向所选原子投影时, 由于所选原子之间并不是正交的关系, 所以会出现同一原子被重复选中的情况, 因而算法需要经过多次迭代才能达到收敛条件, 例如在二维空间中, 信号x可用 $D = [{d_1}, {d_2}]$ 来表示, 那么匹配追踪算法就会在这两个向量之间迭代投影, 即 $x = {a_1}{d_1} + {a_2}{d_2} + $ $ {a_3}{d_1} + {a_4}{d_2}+ \cdots$ 也就是说匹配追踪算法的方向选择不是最优的, 而是次优的.

在匹配追踪算法的基础上, Pati等人提出了正交匹配追踪算法(OMP)^[16]的概念, 正交匹配追踪算法较MP算法的根本性进展就是在将残差信号投影到所选原子之前, 先对所选原子进行施密特正交化处理, 这一步骤使得算法每次迭代的结果都是全局最优解, 收敛速度相较于MP算法有很大提升, 迭代次数大幅减少.

在MP和OMP算法的基础上, 又衍生出了很多相关的贪心算法. 2009年, Needell等人提出了正则正交匹配追踪算法(ROMP)^[17], ROMP算法将贪心算法与凸优化问题相结合, 考虑在匹配时同时选取内积最小的K列, 然后通过正则化约束再进行一遍筛选的方式来提高匹配效率, 最终获得了更快的收敛速度且从含噪声的观测信号中完整的恢复出了原信号. Donoho等人于2012年提出了分段正交匹配追踪算法(StOMP)^[18], 通过设定阈值、选择和投影3个步骤的方式优化了OMP算法.

除此之外, 从自适应的角度出发, 2008年Do等人提出了稀疏度自适应匹配追踪算法(SAMP)^[19], 通过交替估计的方法解决了稀疏度未知的情况. 高睿等人于2010年提出了基于压缩感知的变步长自适应匹配追踪重建算法(VssAMP)^[20], 算法对SAMP的迭代停止条件进行了改进, 只有先后同时满足两个停止条件时才会停止迭代, 如果第一个停止迭代条件不满足则剩余步骤与SAMP相同. 2012年, Sun等人提出了稀疏自适应压缩采样匹配追踪算法(CSAMP)^[21], 采用了回溯线搜索的方式, 降低了算法的复杂度, 具有高精度、自适应性强、高噪声鲁棒性等优点. 2018年王福驰等人引入Dice系数匹配准则改进了自适应匹配追踪算法, 提高了算法的重构质量和运算速度^[22]. 2019年于金冬等人针对稀疏度需要作为先验信息的特点提出利用指数函数的特性对稀疏度进行分段试探, 能够很大程度上降低对稀疏度的依赖, 自适应重构出原始信号的成功率很高^[23]. 同年唐川雁等人针对SAMP算法中原子预选数量超过测量值导致的无法重构的问题, 提出了变比例的稀疏度自适应匹配追踪算法, 在一定程度上提高了重构成功率^[24].

2009年, Needell等人还提出了压缩采样匹配追踪算法(CoSaMP)^[25]的概念, 将限制等距性和剪枝技术等结合到OMP算法的迭代结构中, 该算法在重构信号方面的表现也很出色. 受到压缩采样匹配追踪算法的启发, Dai等人还提出了一种子空间追踪法(SP)^[26], 这种算法大幅提升了优化的效果, 但也显著增大了计算量和算法的复杂度, 2010年杨成等人根据前述算法的研究, 提出了压缩采样中的稀疏度自适应子空间追踪算法(SASP)^[27], 改进了稀疏度初始估计值的估计方法并将弱匹配原则应用到字典原子选取中, 最后通过子空间追踪方法重构信号. 算法的重构效果相对较好, 但时间复杂度略高. 2017年, 为了解决算法应用中出现的重构遮挡情况, 丁函等人提出了贪婪回溯子空间追踪算法, 将正交匹配追踪算法和子空间追踪算法相结合, 提高了算法的实用性^[28].

通过优化算法的结构, Jost等人还提出了一种树基匹配追踪(TMP)算法^[29], 通过构造树形结构字典, 大幅提高了信号稀疏分解的速度, 但同时降低了收敛的速度. 在此基础上La和Do提出了一种新的树基正交匹配追踪(TBOMP)算法^[30], 通过将正交匹配追踪方法与树基匹配追踪算法相结合, 降低了收敛所需时间, 保证了残差经过有限次迭代后能够收敛为零. 基于此, 2013年Gen等人提出了一种新的基于树的回溯正交匹配追踪算法^[31], 该算法将小波树结构转化为候选原子的对应关系, 而不需要任何信号稀疏性的先验信息. 因此, 原子选择过程将更加结构化, 并且可以缩小搜索空间. 此外, 根据回溯过程, 可以检测出先前选择的原子的可靠性, 并在每次迭代中删除不可靠的原子, 最终实现信号的精确重构.

2013年, Karahanoglu和Erdogan创新性的提出了一种具有两个阶段的前向后追踪(Forward-Backward Pursuit, FBP)^[32]方法, 前向阶段目的是扩大支持度估计, 后向阶段是为了去除部分不满意原子, 2019年Meng 等人对前后向追踪算法进行了优化, 提出了改进的自适应前后向追踪算法(IAFBP)^[33], 加快了重建速度的同时克服了自适应过程中存在的过度回溯现象, 提高了算法的准确性.

表1为部分代表性算法的观测样本数量和算法复杂度比较^[34], 其中, N是信号维度, K为稀疏信号非零元个数, b为某常数, 表式创建树的过程中形成的组的大小.

2.2 稀疏表示约束优化算法

对于求解式(3)的方法, 有一种思路就是通过将 ${l_0}$ 范数松弛到 ${l_1}$ 范数, 然后再寻求优化方法, 如式(4)所示:

$\hat s{\rm{ = argmin}}\left\{ {\frac{1}{2}{\rm{||}}x{\rm{ - }}\Psi s{\rm{||}}_2^2{\rm{ + }}\lambda {\rm{||}}s{\rm{|}}{{\rm{|}}_1}} \right\}$

(4)

约束优化算法就是通过这一方式将可微的非约束问题转化为光滑可微的约束优化问题后进行求解, 代表的有3种算法分别是梯度投影稀疏重构算法、内点法和交替方向法. 这些方法是对约束优化方法的有效开发, 具有较好的收敛性. 本文接下来将简单介绍这3类算法各自的特点.

2.2.1 梯度投影稀疏重构算法

梯度投影系数重构算法的核心思想就是构造一个约束函数^[35], 并将约束函数中的 $\alpha $ 分为正负两个部分, 利用矩阵运算进行优化.

根据使用的参量的不同, GPSR又被分为多种其他类型, 常用的为GPSR-Basic算法和GPSR-BB算法. 第1种算法沿负梯度方向进行搜索, 并且采用了一种回溯线搜索的方式使得函数G充分减小^[36], 这种方式保证了每一代的目标函数G值都是减小的. 第2种算法虽然不具备这种特性, 但是由于具有良好的理论支持和计算性能, 因此受到研究者的重视^[37]. 梯度投影稀疏重构算法近年来也得到了迅速的发展, 2011年Deng等人提出了一种新的迭代加权梯度投影算法, 即IWGP^[38], 用于恢复大尺度背景下的稀疏信号, 它减少了对信号处理的不良影响, 提高了梯度投影的计算效率. 2014年Chen等人提出了一种基于梯度的二维稀疏图像重建算法^[39], 大大减少了二维图像重构的时间. 同一时期, Liu等人^[40]提出了一种迭代逼近梯度投影算法. 通过引入一个放松限制变量, 可以将噪声问题转化为等式约束问题, 从而将问题转化为二次规划问题. 基于拟拉格朗日函数和部分对偶的思想, 提出了一种简化算法的思路. 为了进一步提高GPSR-BB算法的性能, 梁丹亚等人于2015年引入了具有全局搜索能力的粒子群优化算法. 利用粒子群算法的全局发展能力和GPSR-BB算法的局部搜索能力, 提高了算法的收敛速度, 降低了算法的运行时间^[41]. 2017年胡剑峰在GPSR-BB算法的技术上进行了改进, 通过对迭代点进行常数步长的预测, 然后根据预测点计算得到新的迭代点并进行校正, 提高了算法的运行速度^[42].

2.2.2 内点法

内点法一般结合牛顿法来使用, 是求解光滑无约束问题的重要方法^[43], 缺陷是迭代求解牛顿方程十分费时. 而一种截断牛顿的方法则能够明显降低求解所需要的时间. 求解大规模的最小化 ${l_1}$ 范数的模型优化问题就可以使用基于截断牛顿的内点法^[44-46]. 求解优化问题时有3个关键步骤, 分别是: (1)将非约束不光滑问题转换为约束光滑问题. (2)利用内点法获得一个新的非约束光滑问题. (3)通过截断牛顿法求解. 截断牛顿内点方法在图像重构、人脸识别、SAR成像等等许多领域都有一定的发展, 为许多研究的进展提供了新的思路. 2018年Corbineau等人从基础的内点法出发, 将算法与一种新的线搜索策略相结合, 提出了一种适用于一般凸约束条件下光滑凸函数和非光滑凸函数之和最小化的近似内点(PIPA)^[47]算法, 优化了算法的效果.

2.2.3 交替方向法

交替方向法的核心思想就是利用变量可分解的性质, 通过对变量的分量分别进行优化来达到优化整体变量的效果^[48], 降低维度, 简化运算, 提高效率. 交替方向法及其一系列衍生算法, 由其求解大规模优化问题时的突出效果, 已经在机器学习、物联网、云计算等等众多领域的大数据优化问题中得到应用, 产生了诸如交替方向乘子法(ADMM)^[49]等一系列算法, 为不同领域大规模数据优化问题做出了重要贡献. 近两年更是在多目标优化调度^[50]、保密能效优化^[51]、嵌入式系统^[52]等领域取得了突出进展. 表2是3类约束优化算法的对比.

2.3 其他稀疏表示优化算法

用于求解稀疏表示模型的优化算法还有很多种类型, 其中比较有代表性的有基于近似算法的稀疏表示优化算法、基于同伦算法的优化算法等.

就像牛顿方法是用于求解非约束光滑模型最小化问题的常用方法, 近似算法可以看作是求解大规模的, 有约束的, 非光滑问题的常用方法, 特别是在涉及高维问题时有比较突出的效果. 近似算法的核心思想是利用近似算子迭代求解子问题, 其计算效率比直接求解原问题高得多. 一般的 ${l_1}$ 范数正则化稀疏表示问题即是一个典型的非光滑凸优化问题, 因而利用近似算法可以有效地解决这个问题. 近似算法还可以细分为软阈值或收缩算子方法、迭代阈值收缩算法、阈值快速迭代收缩算法、基于可分离近似的稀疏重构方法等.

同伦理论是从拓扑学领域延伸出来的, 主要应用于非线性问题求解领域. 同伦技术在稀疏表示中的应用最早源于求解 ${l_1}$ 范数罚函数的最小二乘问题^[53], 其基本思想通过追踪一个参数变化时连续变化的参数路径来求解最优化问题. 与OMP方法相比, 同伦方法更有利于通过在活动集中添加或删除元素来循序渐进地更新稀疏解. 代表算法有LASSO同伦算法^[54]、BPDN同伦算法^[55]、基于同伦方法的 ${l_1}$ 范数重新加权迭代方法等^[54].

3 稀疏表示应用与未来发展展望

目前稀疏表示的应用范畴主要还局限在自然信号领域, 在非自然数据信号领域的应用前景尚不明晰, 根据稀疏表示在各个领域中应用的特点, 可以将稀疏表示的应用类型分为基于重构的应用和基于分类的应用^[56].

基于重构的应用主要有图像去噪^{[57, 58]}、图像信号重构^[59]、音频信号恢复^[60]、压缩感知^[61]、SAR成像^[62]等, 这一类别的应用的共同点即需要先获取目标信号的特征, 利用特征构建稀疏向量, 再利用稀疏表示理论中的数学模型进行求解以达到在可允许的误差范围内重构原信号的效果.

稀疏表示在图像去噪领域的应用相较于空间域去噪和变换域去噪而言有着天然的优势, 后两者的思路分别是将噪声“平摊”到每个像素点和将图像变换到其他频域来去掉噪声比较集中的频率. 对于稀疏表示方法, 稀疏分解的过程会将非稀疏性的噪声信号排除出去, 因而在重构图像的过程中就不会出现噪声信号, 稀疏表示方法也因这一特性而在图像去噪领域拥有巨大的潜能. 现阶段基于稀疏表示的图像降噪方法已经应用到了遥感领域、医学影像处理领域、军事侦察影像处理领域等, 为各个领域的发展都做出了突出的贡献. 与图像去噪理论相似, 基于稀疏表示的图像重构理论在这些领域中也起着至关重要的作用, 稀疏表示图像重构算法基本思路是通过算法获得高分辨率图像和低分辨率图像之间的关系, 通过对高、低频图像块集进行稀疏表示获得对应的字典, 达到对于一幅给定低频成分的图像, 能够重建出其高频部分的效果, 再将二者进行叠加, 从而获得高质量高分辨率图像.

压缩感知技术使得用远低于奈奎斯特采样频率采样信号, 并恢复出原信号成为可能, 而压缩感知技术再信号重构领域使用的稀疏技术使得其与稀疏表示技术在信号重构领域相互交融, 相辅相成. 根据压缩感知技术原理, 信号在某个变换域稀疏, 就能够通过求解最优化问题对原始信号进行重构, 而语音信号恰好具有这一天然特性, 这就是压缩感知技术和稀疏表示技术在音频信号重构领域能够得到应用的原因. 现阶段基于稀疏表示技术的语音信号重构技术已经在语音信号识别、语音分离、信息隐藏等领域做出了重要贡献.

基于分类的应用主要有人脸识别^[63]、目标追踪^[64]、文本检测^[65]、盲源分离^[66]等, 基于分类的应用都是通过提取对象的特征信息构造稀疏的特征向量, 这些特征向量之间具有强烈的区分性, 能够区分不同类别的信号, 再根据稀疏表示的优化方法, 判别目标信号与这些特征向量之间的距离, 在满足一定阈值的时候则判定从属于该类别, 以达到模式识别和分类的效果^[67].

基于稀疏表示的人脸识别是近年来人脸识别领域的研究热门, 2009年Wright等人第一次将稀疏表示技术应用到人脸识别技术中, 算法模型比较简单, 首先通过训练获得过完备字典, 计算最小化 ${l_1}$ 范数约束下的稀疏系数, 然后计算人脸图像与各类别的稀疏系数之间的重构残差, 取最小残差为所属类别. 基于稀疏表示的人脸识别技术拥有模型简单、鲁棒性强、光照影响小、可识别遮挡等的优势, 因而在人脸识别领域得到了迅猛发展.

由于稀疏表示算法具有计算速度快、存储容量要求小、预测新数据速度快等优点, 基于稀疏表示的目标追踪很快就成为了目标追踪领域的热门研究方向, 目前基于稀疏表示的目标追踪已经应用到了军事领域、交通运输监测、安全监控、人机交互、医学领域、视觉导航等领域, 优化了各个领域目标追踪的效果.

盲源分离技术是为了解决输入未知、传输信道未知而输出已知的信号处理技术, 而稀疏表示技术通过分开混合矩阵的估计过程和源信号的估计过程的方式降低了算法复杂度, 提高了源信号分离精度, 成为了当前盲源分离问题中的热门方法.

4 结束语

近年来稀疏表示经历了迅猛的发展, 但其中仍有很多问题值得深入研究. 例如稀疏表示模型的灵活性还有待提高^[68], 现有稀疏表示算法的目标基本都放在了求最稀疏的解上, 但在实际表示时可能会存在多目标干扰, 此时若一味追求最稀疏的解, 很可能无法得到最优解, 例如在图像重构时^[69], 如果仅考虑稀疏解, 就可能会导致目标丢失的现象, 因此需要更为灵活的稀疏表示模型来应对多目标干扰时出现的问题. 稀疏表示算法的自适应性也有待提高, 现存的很多算法采用的还是预先给定参数, 再根据结果修改参数的方式进行求解, 这样势必会导致工作量倍增且自动化程度受限, 这就限制了算法在很多自动化要求较高的领域中的应用. 除此之外, 现有的稀疏表示模型基本都建立在目标函数为线性函数且只含高斯白噪声的基础上, 传统的稀疏表示算法的目的也是获得观测信号的线性表示, 这就意味着稀疏表示在处理图像、声音等信号时有着不错的效果, 但面对非自然信号时就束手无策了, 因此要想获得更为广阔的应用空间, 就仍需对算法原理进一步改进.