粒子群优化算法(Particle Swarm Optimization, PSO)是由Kennedy和Eberhart [1]提出的模拟鸟群觅食行为的一种群体协作随机优化方法. PSO算法中每个粒子都代表一个问题的候选解, 通过粒子个体的简单行为及群体内的信息交互实现问题求解的智能性. 其概念简单、实现容易、鲁棒性强、优化性能好, 常用于解决多峰值、非线性等问题, 并在函数优化[2]、图像处理[3]、系统辨识[4]、神经网络[5]、有限元模型修正[6]等工程和科学领域得到广泛应用.
虽然PSO算法优化性能较好, 但也存在早熟收敛、容易陷入局部极值、迭代后期收敛速度慢等问题. 对此, 国内外研究学者从调整算法自身参数、改变粒子学习模式、结合其他优化算法等方向提出诸多改进的方法. 吴静等人[7]通过动态调整惯性权重, 提高了算法收敛速度及稳定性. 张继荣等人[8]提出一种惯性权重余弦调整的PSO算法, 提高了算法的精度. 李龙澍等人[9]为平衡粒子的搜索行为提出了一种新的自适应惯性权重混沌PSO算法, 提高算法全局探索能力. 谭阳等人[10]改变粒子学习模式, 将PSO中指导粒子群进化的全局最优解扩展为由多个精英粒子组成的精英子群, 提高了算法跳出局部极值的能力. Liang等人[11]提出了一种综合学习PSO算法, 在多峰函数上具有较好的优化效果. Jiang等人[12]将遗传算法中杂交算子引入到PSO算法中, 有效提高了算法的收敛性. Xia等人[13]在PSO算法中引入变异算子对人行桥进行模型修正, 算法收敛速度和精度得到提高, 得到令人满意的修正结果. 刘波等人[14]提出了一种混合模拟退火算法的改进PSO算法, 提高了算法收敛到全局最优解的速度和精度. 张庭场等人[15]提出一种融合裂变和变异操作的分合群PSO算法, 提高了算法局部收敛能力. 这些改进算法大都要么提高了算法的收敛速度和精度, 即提高算法局部挖掘能力, 要么增强算法跳出局部极值的能力, 即提高算法全局探索能力, 很难同时兼顾两者.基于以上研究, 为有效地兼顾了全局探索与局部挖掘能力, 提出了一种融合多种策略的改进粒子群算法(Improved Particle Swarm Optimization Algorithm, IPSO). 实验结果表明, IPSO同其他PSO算法相比, 收敛速度快、求解精度高且容易跳出局部最优解.
1 基本PSO算法PSO算法是一种基于群智能的随机搜索算法, 源于对鸟群捕食行为的研究. PSO算法由一群粒子组成, 每个粒子可视为D维搜索空间中的一个搜索个体, 具有自身的位置和速度, 并且能够保留迄今为止所找到的最优位置以及所有粒子目前找到的全局最优位置.算法迭代过程中, 每个粒子根据个体最优位置和全局最优位置来更新自己的速度和位置, 通过目标函数适应度值来评价粒子更新的位置是否更优, 从而不断进化来获得新的个体最优和全局最优位置. 在标准PSO算法中, 粒子迭代更新公式如下:
| ${\bf{v}}_i^{t + 1} = \omega {\bf{v}}_i^t + {c_1}{r_1}\left( {{\bf{p}}_i^t - {\bf{x}}_i^t} \right) + {c_2}{r_2}\left( {{\bf{p}}_g^t - {\bf{x}}_i^t} \right)$ | (1) |
| ${\mathbf{x}}_i^{t + 1} = {\mathbf{x}}_i^t + {\mathbf{v}}_i^{t + 1}$ | (2) |
式中,
惯性权重
| $\omega = {\omega _{\max }} - \frac{{{\omega _{\max }} - {\omega _{\min }}}}{{{G_{\max }}}} \cdot t$ | (3) |
其中,
粒子的飞行速度
本文融合了多种策略对基本PSO进行改进. 首先, 受达尔文 “优胜劣汰、适者生存”生物进化思想[16]的启发, 对种群粒子进行选择, 适应度值小的优良种群被保留, 其它粒子则被淘汰, 具体实施中采取了分组策略和精英策略. 按适应度值从小到大排序将种群分为优解组和劣解组, 优解组进行遗传交叉操作, 劣解组进行变异操作; 然后将经过交叉变异后的种群和当前迭代次数下的初始种群按适应度值从小到大进行排序, 选出前一半粒子作为更新种群. 其次, 采取改进粒子学习模式的策略, 充分利用了群体信息, 保证了种群的多样性, 提高了算法全局探索的能力. 最后, 采取了控制概率的策略, 通过引入决策数P, 控制进入交叉变异等操作的概率, 使算法在迭代初期小概率执行交叉变异等操作, 尽量增加种群多样性, 保证算法的全局探索的能力; 随迭代次数的增加, 进入交叉变异等操作的概率逐渐增大, 迭代后期的收敛速度显著加快, 算法的局部挖掘能力得到增强. 通过多种策略的融合, IPSO算法能有效兼顾全局探索和局部挖掘能力, 具有收敛速度快、求解精度高、避开局部最优解的优点.
2.1 分组策略根据目标函数的适应度值对种群进行分组. 首先生成包含N个粒子的初始种群, 计算种群内所有粒子目标函数的适应度值
| $\hat x_i' = \eta {\hat x_{{ {index}}1(i)}} + (1 - \eta ){\hat x_{{ {index}}2(i)}},{\rm{ }}i = 1,2,\cdots,\hat N$ | (4) |
其中
劣解组进行变异操作, 通过变异生成优良基因, 充分利用每个粒子信息, 如式(5)所示:
| $\tilde x_i^{''} = \left\{ \begin{gathered} {{\tilde x}_i} + ({{\tilde x}_i} - {x_{\max }}) \times f(t){\rm{ }},\;r \ge 0.5 \\ {{\tilde x}_i} + ({{\tilde x}_i} - {x_{\min }}) \times f(t){\rm{ }},\;r < 0.5 \\ \end{gathered} \right.$ | (5) |
式中,
将优解组通过交叉生成的新种群
个体除总结自身的实践经验和向最优个体学习外, 也学习其他优秀同伴的行为, 尤其在进化初期, 这种行为在个体的学习中应处于主导地位. 为充分利用群体信息, 从排序后的种群中选出前1/4粒子, 以这些粒子的均值代替个体最优指导粒子搜索, 以保证种群的多样性. 对基本PSO算法中的个体极值
| ${{\mathbf{\bar p}}^t} = \sum\limits_{j = 1}^m {{\mathbf{p}}_j^t} /m$ | (6) |
其中,
| ${\bf{v}}_i^{t + 1} = \omega {\bf{v}}_i^t + {c_1}{r_1}\left( {{{{\bf{\bar p}}}^t} - {\bf{x}}_i^t} \right) + {c_2}{r_2}\left( {{\bf{p}}_g^t - {\bf{x}}_i^t} \right)$ | (7) |
引入一个随机决策数P, P是以迭代次数
| $ P=0.1+0.{9}{\rm e}^{-10·t/{G}_{\mathrm{max}}}$ | (8) |
若
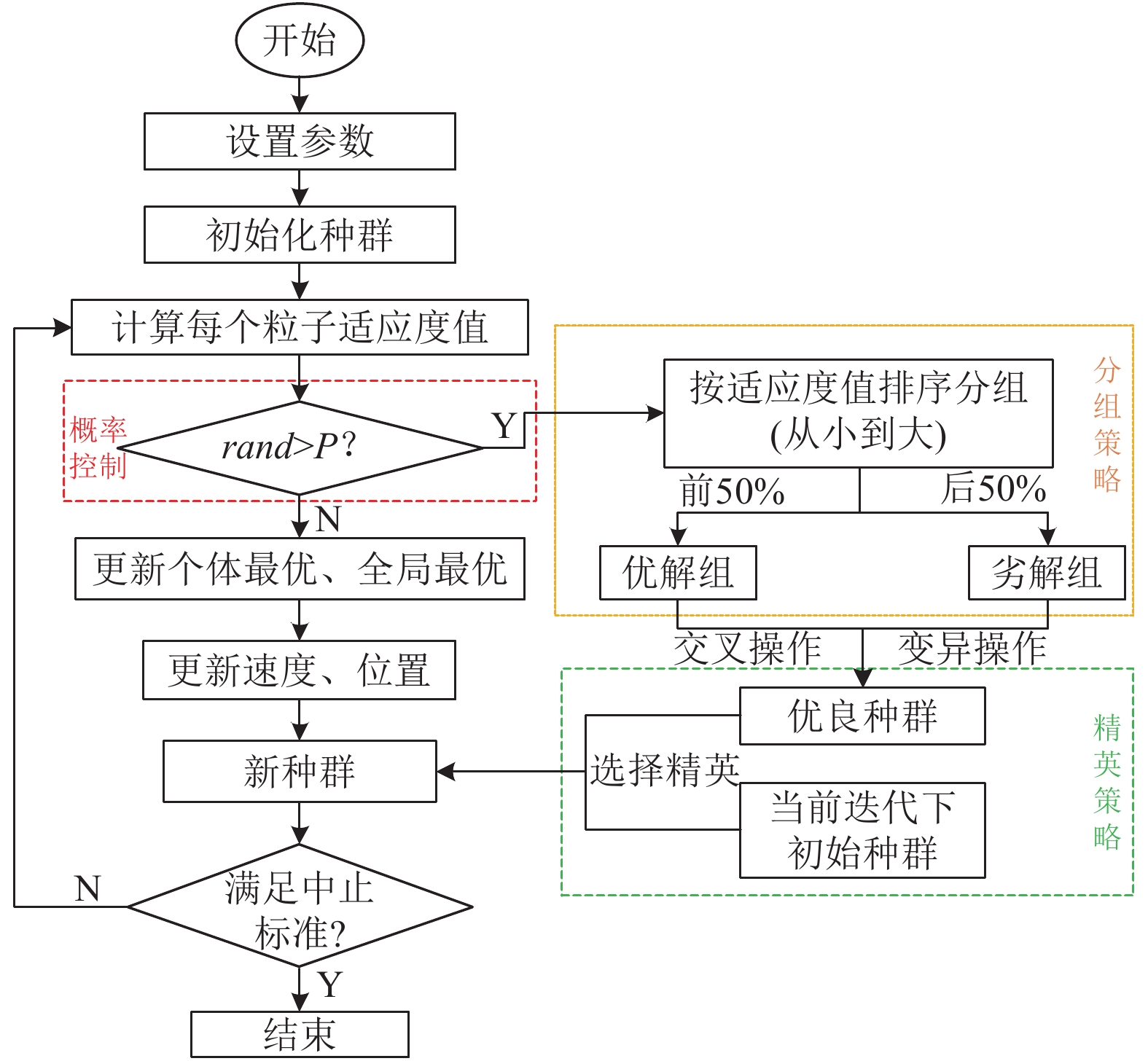
对IPSO算法流程描述如下, 图1给出了IPSO算法流程图.
|
图 1 IPSO算法流程图 |
Step 1. 设置算法参数;
Step 2. 随机初始化种群;
Step 3. 计算每个粒子适应度值;
Step 4. 判断是否进入交叉变异操作, 若
Step 5. 根据适应度值按升序排列粒子, 前50%个粒子被定义为优解组, 其余为劣解组, 优解组进行交叉操作, 劣解组进行变异操作, 产生新的种群;
Step 6. 将经过交叉变异后新产生的种群与当前迭代次数下的初始种群合并形成扩大种群, 按适应度值升序排列, 选出前一半粒子作为精英种群用于更新迭代;
Step 7. 按式(6)更新个体最优, 更新全局最优;
Step 8. 更新粒子位置和速度;
Step 9. 判断是否满足迭代中止标准, 若迭代次数达到最大迭代次数
实验环境为: Matlab R2014b, CPU为i7-6500U@2.5 GHz, 选取基本PSO[1], BreedPSO[12], SimuAPSO[14]三种算法与本文提出的IPSO算法进行比较. 算法参数的设置同原文献相同, 对于BreedPSO, 杂交概率取0.9, 杂交池的大小取0.2; 对于SimuAPSO, 退火常数取0.5. 各优化方法共有参数均保持一致, 种群规模取400, 最大迭代次数为200, 学习因子均取2.
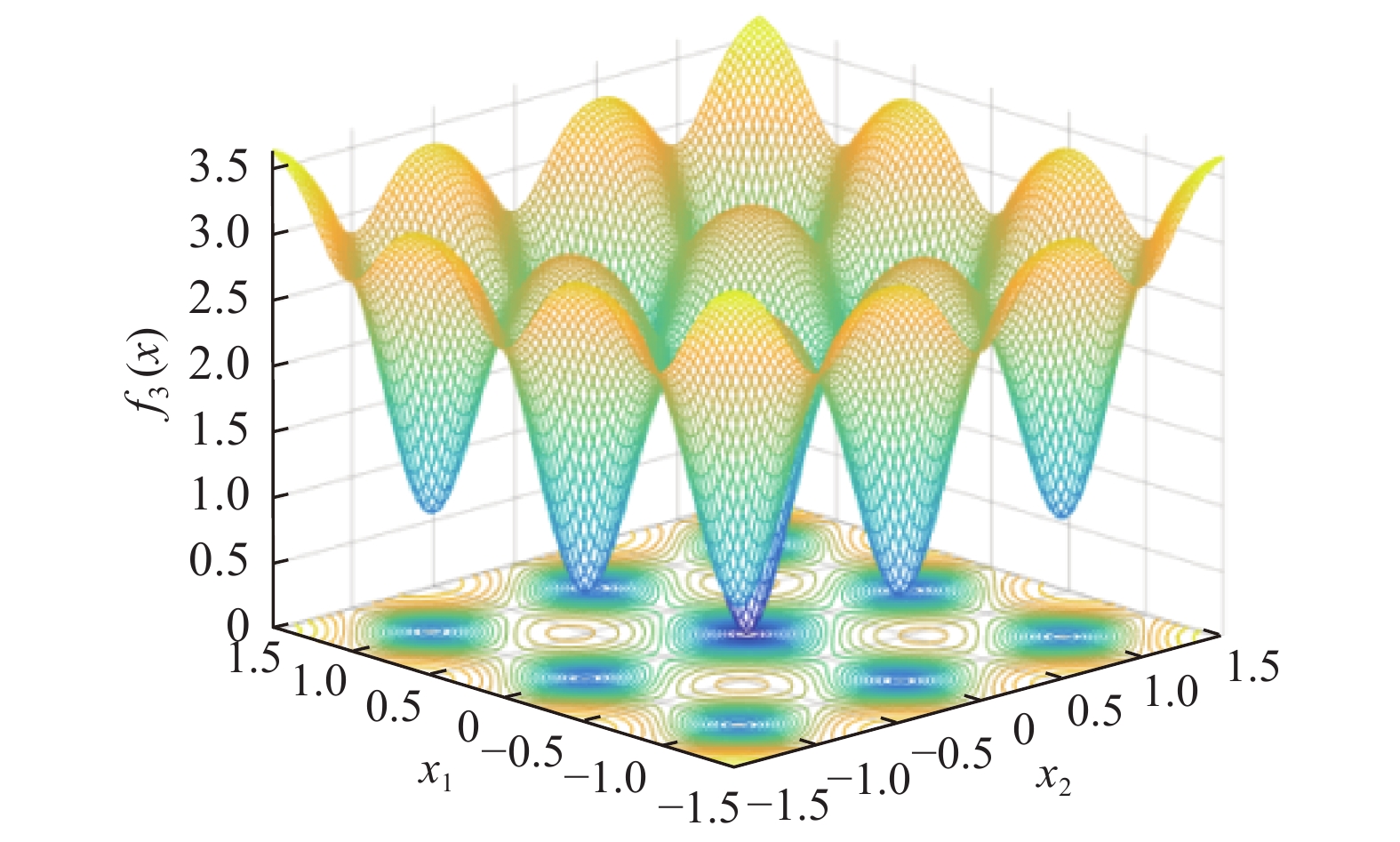
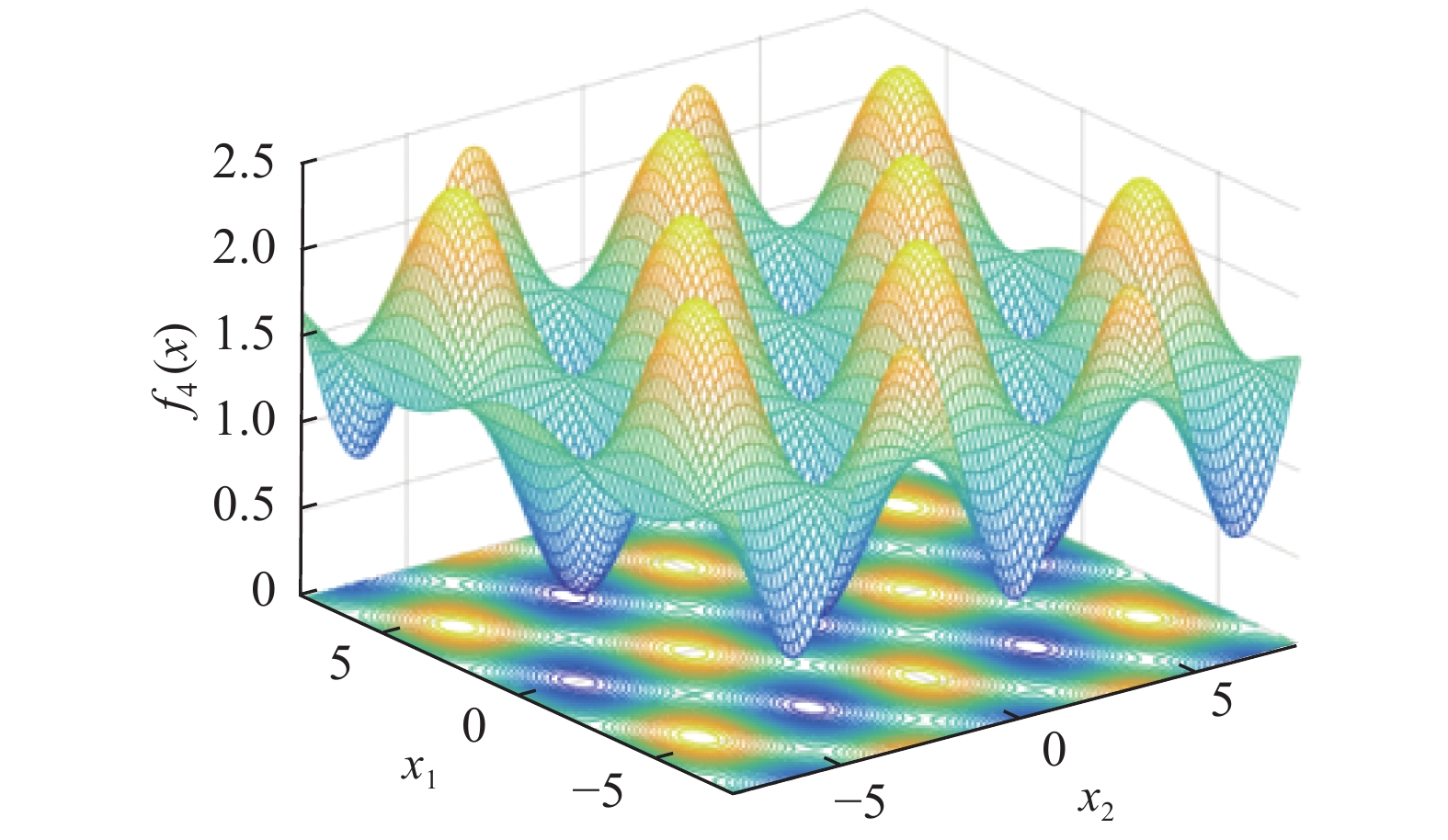
3.2 测试函数从GEATbx中选取4个标准测试函数, 测试函数维数取10维, 分别对IPSO算法和其他改进PSO算法性能进行了比较. 其中f1、f2为单峰函数, f1用于检验算法的收敛速度和精度; f2最优位置是在一个狭长的, 抛物线形的扁平山谷内, 可认为拥有无数个局部极值, f3、f4为多峰函数, 其二维函数图像如图2、图3所示, 其局部极值的个数随维数的增加成几何级增加, f2、f3、f4主要用于检验算法跳出局部极值, 全局搜索的能力,同时也能检验其收敛速度和精度. f1、f3、f4函数的全局最优均为: 当
|
图 2 Ackley’s Path二维函数图像 |
|
图 3 Griewank二维函数图像 |
(1) Sphere球函数:
| ${f_1}(x) = \sum\limits_1^n {x_i^2} $ | (9) |
(2) Rosenbrock函数:
| ${f_2}(x) = \sum\limits_{i = 1}^{n - 1} {\left( {100{{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{(1 - {x_i})}^2}} \right)} $ | (10) |
(3) Ackley’s Path函数:
| ${f_3}(x) = - 5 \cdot {{\rm e}^{ - 0.2 \cdot \sqrt {\frac{{\sum\limits_{i = 1}^n {x_i^2} }}{n}} }} - {{\rm e}^{\frac{{\sum\limits_{i = 1}^n {\cos (2\pi \cdot {x_i})} }}{n}}} + 5 + {{\rm e}^1}$ | (11) |
(4) Griewank函数:
| ${f_4}(x) = \sum\limits_{i = 1}^n {\frac{{x_i^2}}{{4000}}} - \prod\limits_{i = 1}^n {\cos \left( {\frac{{{x_i}}}{{\sqrt i }}} \right)} + 1$ | (12) |
| 表 1 测试函数f1优化的结果 |
| 表 2 测试函数f2、f3、f4优化的结果 |
|
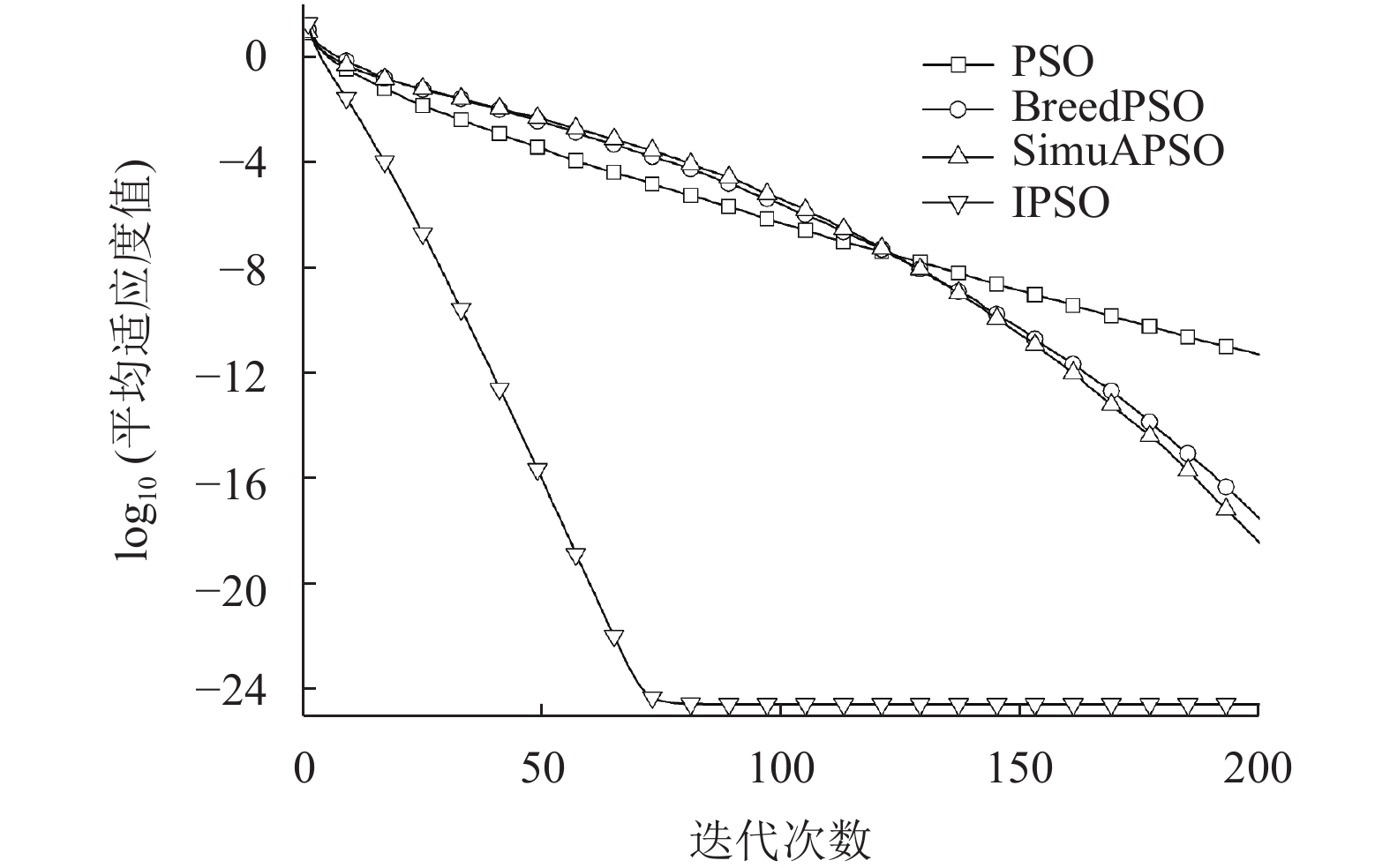
图 4 f1平均适应度值的对数迭代曲线 |

|
图 5 f2平均适应度值的对数迭代曲线 |

|
图 6 f3平均适应度值的迭代曲线 |
|
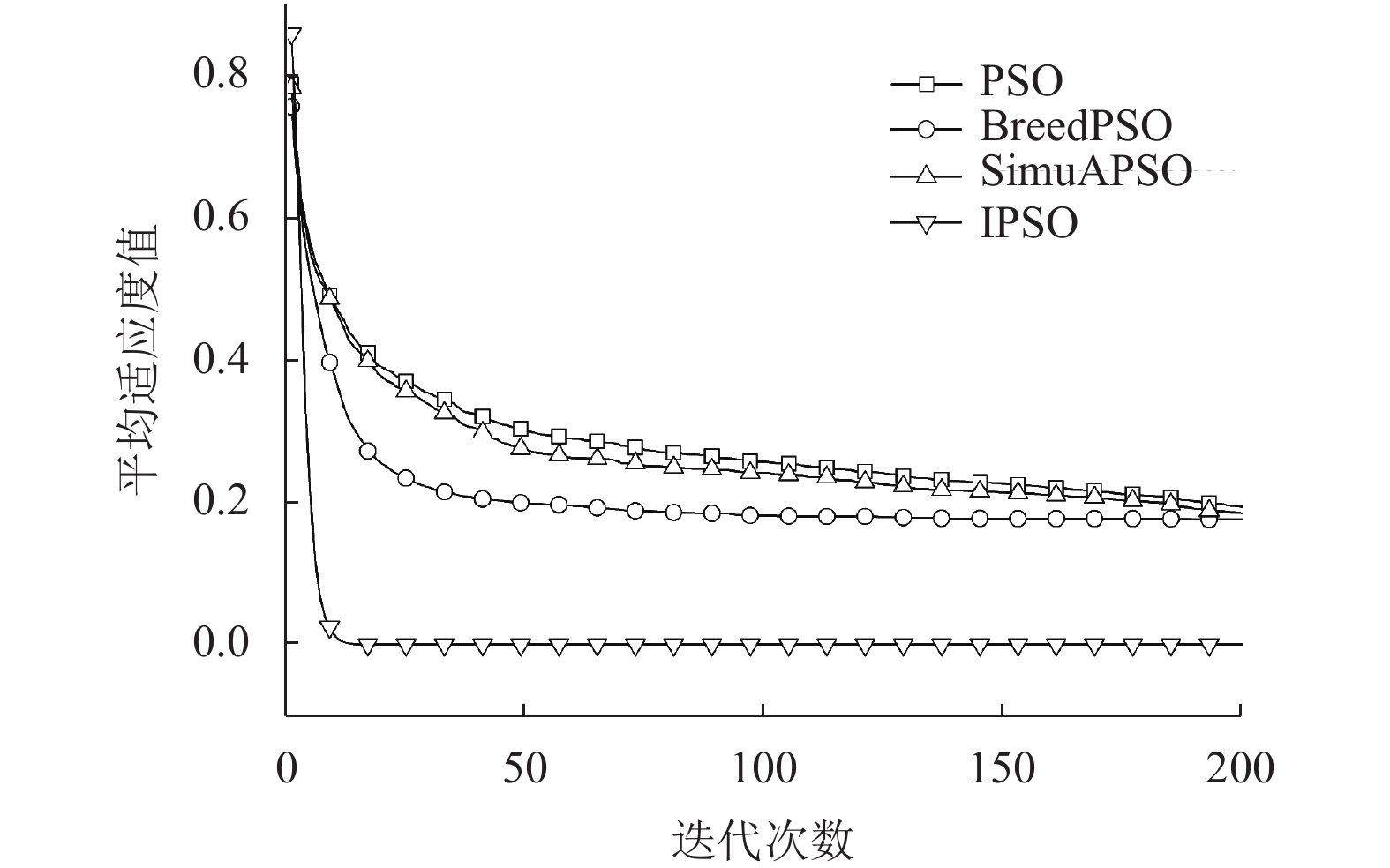
图 7 f4平均适应度值的迭代曲线 |
3.3 仿真结果分析
从表1和表2可知, IPSO算法分别对4个测试函数进行100次计算得到的适应度值均值和方差均小于其他PSO算法, 表明IPSO算法收敛速度快, 搜索精度高, 稳定性好. 对于测试函数f1, IPSO算法计算得到适应度值均值为3.03E–25, 相比其他PSO算法, 搜索精度显著提高, 在最佳目标成功率上, 100%达到10−20数量级, 优化到10−40以下成功率达到45%, 远远优于其他PSO算法. 另外, 在相同条件下运行时间, IPSO算法要比基本PSO耗时长, 与SimuAPSO相当, 比BreedPSO耗时短, 从取得的优化效果来看, 增加的时间完全可以接受.
图4–图7中平均适应度值收敛曲线显示了IPSO算法下降速度快, 达到稳定时迭代次数少, 稳定时平均适应度值远低于其他PSO算法, 进一步证实IPSO算法具有收敛速度快、精度高的特点. 从表2可知, IPSO算法在提高收敛速度和精度的同时, 跳出局部极值成功搜索到全局最优解的能力显著提升, 对于测试函数f2, 搜索到全局最优 (1,…,1)附近位置, IPSO算法成功率达到56%, 而其他PSO算法均小于30%, 对于测试函数f3, 搜索到全局最优 (0,…,0)附近位置, IPSO算法成功率高达96%, 而其他PSO算法均小于30%. 测试函数f4对比于f3, 其局部极值与全局最优位置对应的适应度值相差很小且局部极值数量庞大, 因此很难找到全局最优位置, IPSO算法找到最优解(0,…,0)位置的成功率为90%, 而其他PSO算法均很难找到最优解位置.
4 结论本文针对PSO算法容易陷入局部极值及进化后期收敛速度慢、精度低等缺点, 提出了一种融合多种策略的改进粒子群算法(IPSO). 该算法采取了分组控制、精英选择、改变学习模式、引入概率等策略, 通过实验仿真结果证明了IPSO算法同其他PSO算法相比, 收敛速度快、求解精度高且容易跳出局部最优解. IPSO算法的全局探索和局部挖掘能力均得到明显提升, 较为有效地兼顾了全局与局部寻优.
| [1] |
Kennedy J, Eberhart RC. Particle swarm optimization. Proceedings of International Conference on Neural Networks (ICNN’95). Perth, WA, Australia. 1995. 1942–1948.
|
| [2] |
夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法. 计算机学报, 2015, 38(7): 1397-1407. DOI:10.11897/SP.J.1016.2015.01397 |
| [3] |
Verma R, Mehra R. PSO algorithm based adaptive median filter for noise removal in image processing application. International Journal of Advanced Computer Science and Applications, 2016, 7(7): 92-98. |
| [4] |
Bian Q, Zhao KR, Wang XM, et al. System identification method for small unmanned helicopter based on improved particle swarm optimization. Journal of Bionic Engineering, 2016, 13(3): 504-514. DOI:10.1016/S1672-6529(16)60323-2 |
| [5] |
王荣, 白尚旺, 党伟超, 等. 粒子群退火算法优化的BP神经网络及其应用. 计算机系统应用, 2020, 29(1): 244-249. DOI:10.15888/j.cnki.csa.007220 |
| [6] |
秦世强, 胡佳, 曹鸿猷, 等. 基于试验数据的大跨度拱桥有限元模型修正. 中国公路学报, 2019, 32(7): 66-76. |
| [7] |
吴静, 罗杨. 动态调整惯性权重的粒子群算法优化. 计算机系统应用, 2019, 28(12): 184-188. DOI:10.15888/j.cnki.csa.007162 |
| [8] |
张继荣, 张天. 基于改进粒子群算法的PID控制参数优化. 计算机工程与设计, 2020, 41(4): 1035-1040. |
| [9] |
李龙澍, 张效见. 一种新的自适应惯性权重混沌PSO算法. 计算机工程与应用, 2018, 54(9): 139-144. DOI:10.3778/j.issn.1002-8331.1612-0093 |
| [10] |
谭阳, 唐德权, 全惠云. 一种排异竞争的粒子群优化算法. 系统仿真学报, 2011, 23(12): 2635-2640, 2646. |
| [11] |
Liang JJ, Qin AK, Suganthan PN, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295. DOI:10.1109/TEVC.2005.857610 |
| [12] |
Jiang JH, Li X, Deng ZH, et al. Control-oriented dynamic model optimization of steam reformer with an improved optimization algorithm. International Journal of Hydrogen Energy, 2013, 38(26): 11288-11302. DOI:10.1016/j.ijhydene.2013.06.103 |
| [13] |
Xia ZY, Li AQ, Li JH, et al. FE model updating on an in-service self-anchored suspension bridge with extra-width using hybrid method. Applied Sciences, 2017, 7(2): 191. DOI:10.3390/app7020191 |
| [14] |
刘波, 张焰, 杨娜. 改进的粒子群优化算法在分布式电源选址和定容中的应用. 电工技术学报, 2008, 23(2): 103-108. DOI:10.3321/j.issn:1000-6753.2008.02.017 |
| [15] |
张庭场, 耿光飞. 基于改进粒子群算法的中压配电网无功优化. 电网技术, 2012, 36(2): 158-162. |
| [16] |
Darwin C. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: John Murray, Albemarle Street, 1859.
|
 2021, Vol. 30
2021, Vol. 30



