当前, 深度神经网络模型在视觉[1]、文本[2]和语音[3]等任务上都有着非常好的表现. 但是随着神经网络层数的加深, 模型的训练变得越来越困难. 因此, 研究人员开始关注优化方法. 随机梯度下降法(SGD)是求解优化问题的一种简单有效的方法, SGD被广泛应用于实际问题[4]. 该方法根据小批量(mini-batch)样本的可微损失函数的负梯度方向对模型参数进行更新, SGD具有训练速度快、精度高的优点. 但由于其参数是每次按照一个小批量样本更新的, 因此如果每个小批量样本的特性差异较大, 更新方向可能会发生较大的变化, 这导致了它不能快速收敛到最优解的问题. 因此, SGD有很多变种, 一般可以分为两类. 第一类是学习率非自适应性方法, 使用梯度的一阶矩估计——SGDM[5], 结合每个小批量样本的梯度求滑动平均值来更新参数, 极大地解决了SGD算法收敛速度慢的问题, 这个方法目前应用非常广泛, 本文就针对这个方法进行改进. 第二类是学习率自适应性方法, 利用梯度的二阶矩估计实现学习率的自适应调整, 包括AdaGrad[6], RMSProp[7], AdaDelta[8], Adam[9]. 其中Adam是深度学习中最常见的优化算法, 虽然Adam在训练集上的收敛速度相对较快, 但在训练集上的收敛精度往往不如非自适应性优化方法SGDM, 且泛化能力不如SGDM. AmsGrad[10]是对Adam的一个重要改进, 但是最近的研究表明, 它并没有改变自适应优化方法的缺点, 实际效果也没有太大改善. RAdam[11]是Adam的一个新变体, 可以自适应的纠正自适应学习率的变化.
目前很多研究都集中在第二类学习率自适应性方法上, 却忽略了最基本的问题. 无论自适应还是非自适应方法都用了指数滑动平均法, 这些方法都试图用指数滑动平均得到近似样本总体的梯度, 然而这种方法是有偏且具有滞后性的. 针对这一问题我们提出了RSGDM算法, 我们的方法计算梯度的差分, 即计算当前迭代梯度与上一次迭代梯度的差, 相当于梯度的变化量, 我们在每次迭代时使用指数滑动平均估计当前梯度的变化量, 然后用这一项与当前梯度的估计值进行加权求和, 这样的做法可以降低偏差且缓解滞后性.
1 RSGDM算法算法1. RSGDM算法: 所有向量计算都是对应元素计算
输入: 学习率
随机初始化参数向量
While
计算t时间步长上随机目标函数的梯度:
计算差分:
更新梯度和差分的一阶矩估计:
用差分的一阶矩估计修正对梯度的估计:
更新参数:
end While
输出: 结果参数
算法1展示了RSGDM算法的整体流程. 设
1) SGDM算法:
| ${m_t} = \beta *{m_{t - 1}} + (1 - \beta )*{g_t}$ | (1) |
| ${\theta _t} = {\theta _{t - 1}} - \alpha *{m_t}$ |
2) RSGDM算法:
| ${m_t} = \beta *{m_{t - 1}} + (1 - \beta )*{g_t}$ |
| ${{\textit{z}}_t} = \beta *{{\textit{z}}_{t - 1}} + (1 - \beta )*\Delta {g_t}$ | (2) |
| ${n_t} = {m_t} + \beta *{{\textit{z}}_t}$ | (3) |
| ${\theta _t} = {\theta _{t - 1}} - \alpha *{n_t}$ |
可以看出, RSGDM算法比SGDM算法多出式(2)和式(3), 本文第2节将证明SGDM中的式(1)
首先我们分析用指数滑动平均估计总体梯度的偏差, 首先由SGDM算法中的式(1)可以得到:
| ${m_t} = (1 - \beta )*\sum\limits_{i = 1}^t {{\beta ^{t - i}}*{g_i}} $ | (4) |
对式(4)两边取期望可得:
| $\begin{split} E({m_t}) =& (1 - \beta )*E\left( {\sum\limits_i^t {{\beta ^{t - i}}*{g_i}} } \right)= (1 - \beta )*\left[ {{\beta ^{t - 1}}*E({g_1})} \right.\\ & +\left. { {\beta ^{t - 2}}*E({g_2}) + \cdots + \beta *E({g_{t - 1}}) + E({g_t})} \right]\\ =& \left( {1 - {\beta ^t}} \right)*E({g_t}) + (1 - \beta )*\xi \end{split} \!\!\!\!\!\!\!\!\!\!\!\!$ | (5) |
可以发现
| $\begin{split} \xi =& \sum\limits_{i = 1}^t {{\beta ^{t - i}}\left[ {E({g_i}) - E({g_t})} \right]} = {\beta ^{t - 1}}*\left[ {{g_1} - E({g_t})} \right]\\ & + {\beta ^{t - 2}}*\left[ {{g_2} - E({g_t})} \right] + \cdots + \beta *\left[ {{g_{t - 1}} - E({g_t})} \right] \end{split}$ | (6) |
当迭代次数较多时,
首先由式(2), 我们可以得到:
| ${{\textit{z}}_t} = (1 - \beta )*\sum\limits_{i = 2}^t {{\beta ^{t - i}}*\Delta {g_i}} $ | (7) |
对RSGDM算法中的式(3)两边取期望, 我们可以得到:
| $E({n_t}) = \left( {1 - {\beta ^t}} \right)*E({g_t}) + (1 - \beta )*\xi + \beta (1 - \beta )*\left( {\sum\limits_{i = 2}^t {{\beta ^{t - i}}*\Delta {g_i}} } \right)$ | (8) |
| $ \begin{split} \varsigma =& \sum\limits_{i = 1}^{t - 2} {{\beta ^{t - i}}*[{g_{i + 1}} - E({g_t})]} = {\beta ^{t - 1}}*[{g_2} - E({g_t})] \\ & +{\beta ^{t - 2}}*[{g_3} - E({g_t})] + \cdots + {\beta ^2}*[{g_{t - 1}} - E({g_t})] \end{split} $ | (9) |
我们对比式(6)SGDM算法的偏差项
本节我们通过实验证明我们的RSGDM算法比SGDM算法更有优势. 我们选择图像分类任务来验证算法的优越性, 实验使用了CIFAR-10和CIFAR-100数据集[12]. CIFAR-10数据集和CIFAR-100数据集均由32×32分辨率的RGB图像组成, 其中训练集均是50000张图片, 测试集10000张图片. 我们在CIFAR-10数据集上进行10种类别的分类, 在CIFAR-100数据集上进行100种类别的分类. 我们分别使用ResNet18模型和ResNet50[13]模型在CIFAR-10和CIFAR-100数据集上进行图像分类任务, 每个任务使用SGDM算法和我们的RSGDM算法进行比较, 评价的指标为分类的准确率. 我们使用的深度学习框架是PyTorch, 训练的硬件环境为单卡NVIDIA RTX 2080Ti GPU. 实验中的批量大小(batch-size)设置为128, SGDM算法和RSGDM算法的两个超参数设置一样, 其中动量
表1和表2分别给出了ResNet18和ResNet50使用不同的优化器在CIFAR-10和CIFAR-100数据集上图像分类的准确率. 我们可以看到在CIFAR-10数据集上, SGDM和RSGDM训练精度都达到了100%, 测试精度我们的RSGDM比SGDM高了0.14%. 在CIFAR-100数据集上, SGDM和RSGDM训练精度都是99.98%, 在测试精度上RSGDM比SGDM高了0.57%.
| 表 1 ResNet18在CIFAR-10上分类准确率(%) |
| 表 2 ResNet50在CIFAR-100上分类准确率(%) |
图1–图4给出了ResNet18在CIFAR-10上使用SGDM算法和RSGDM算法的实验结果, 包括训练准确率、训练损失、测试准确率、测试损失. 由于我们实验设置每50个epoch学习率减半, 很明显可以看出4张图在epoch50、100、150均有一些波动. 总体上看在训练准确率和训练损失上, 两种方法无论收敛速度和收敛精度都大体相同, 在收敛精度上训练后期我们的RSGDM算法更具优势.
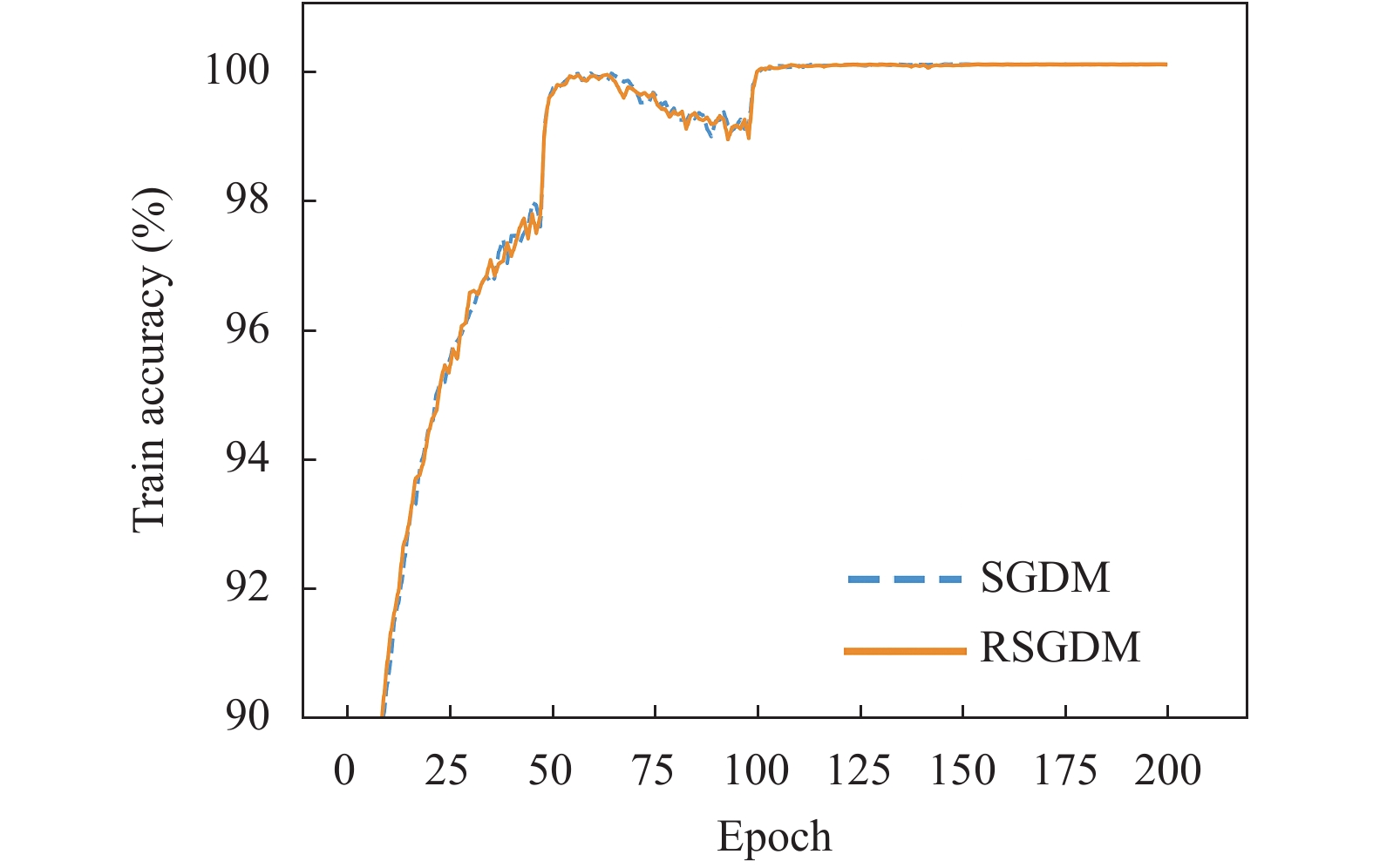
|
图 1 ResNet18在CIFAR-10上的训练准确率 |
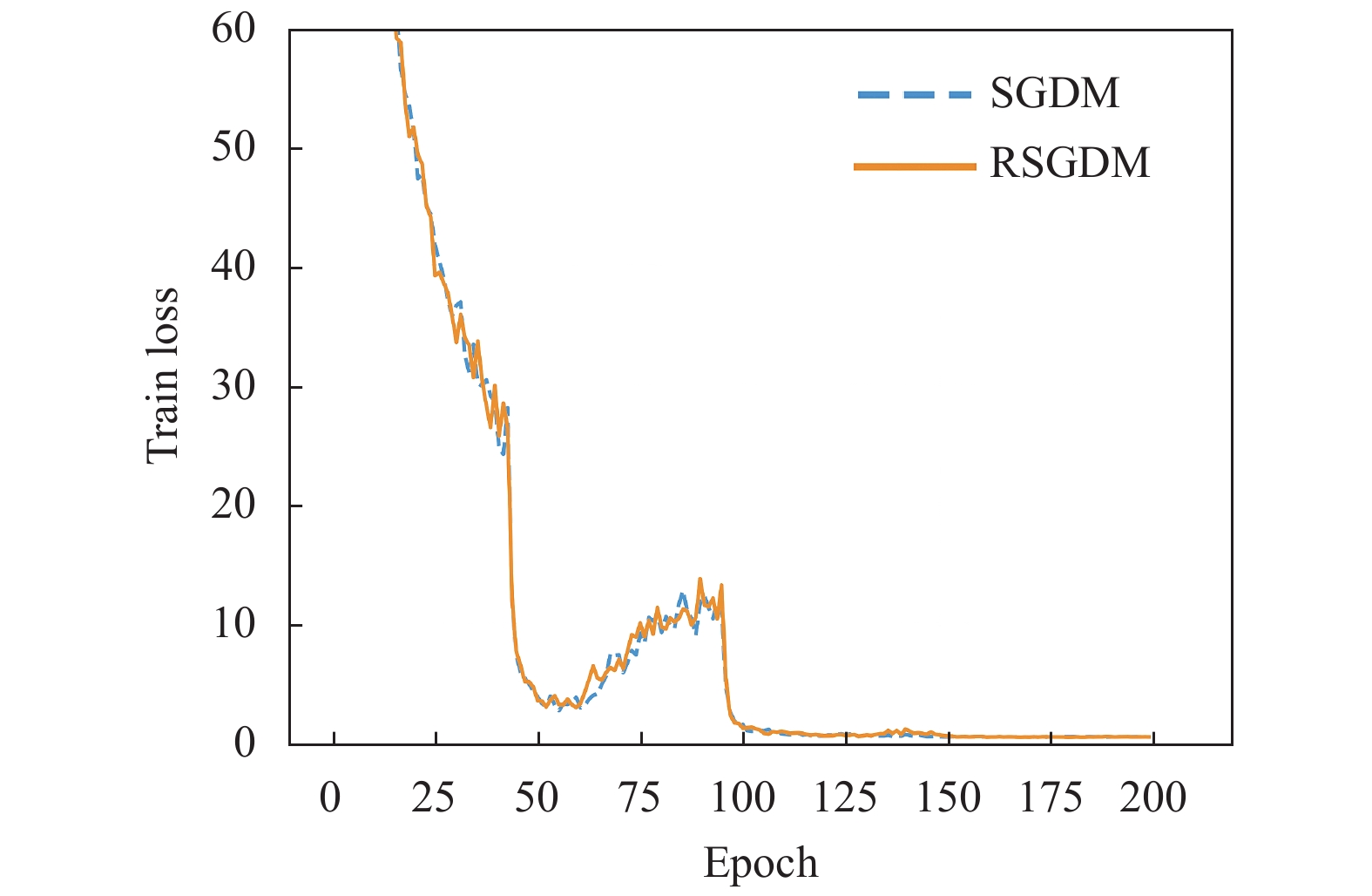
|
图 2 ResNet18在CIFAR-10上的训练损失 |
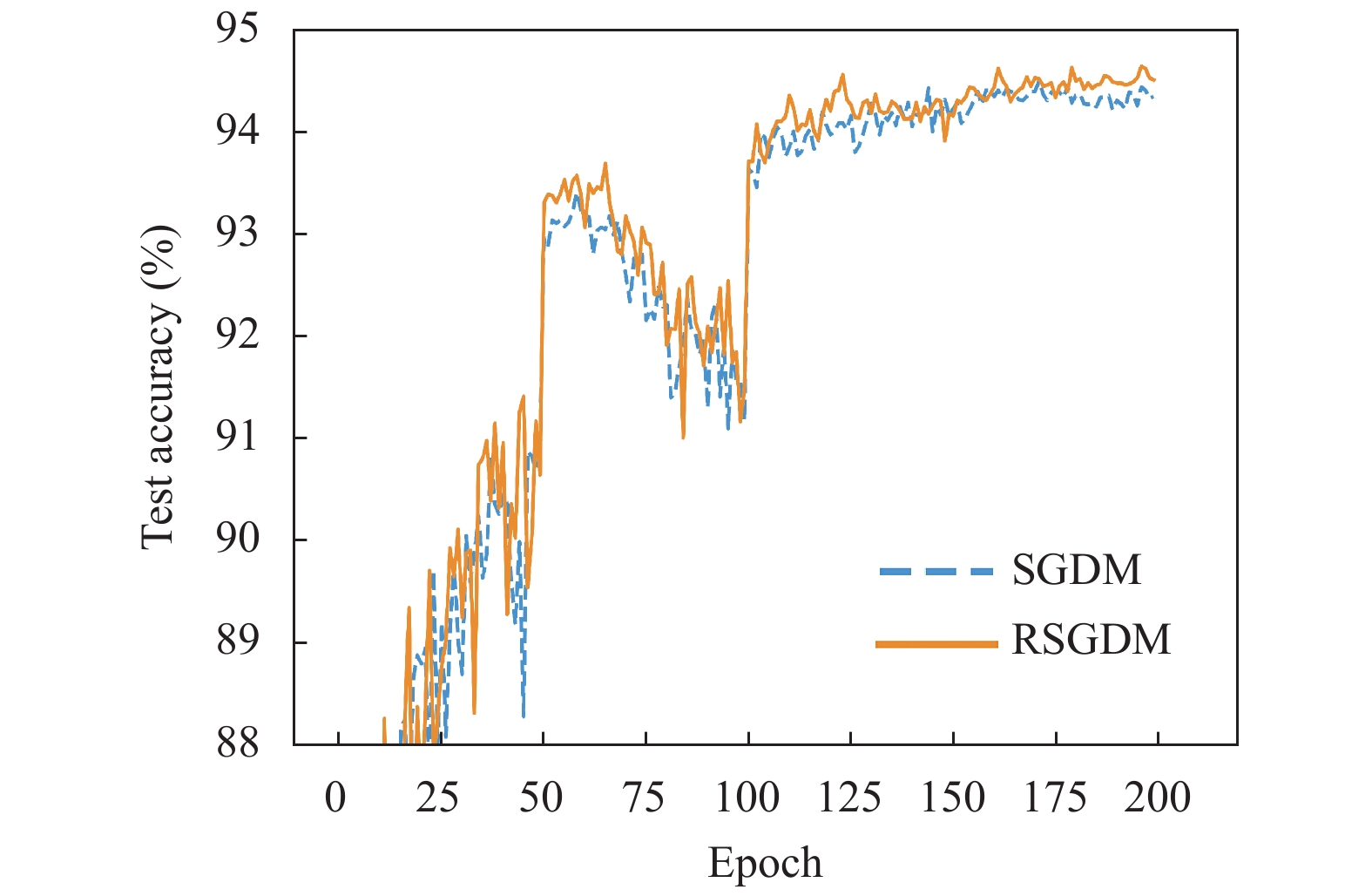
|
图 3 ResNet18在CIFAR-10上的测试准确率 |
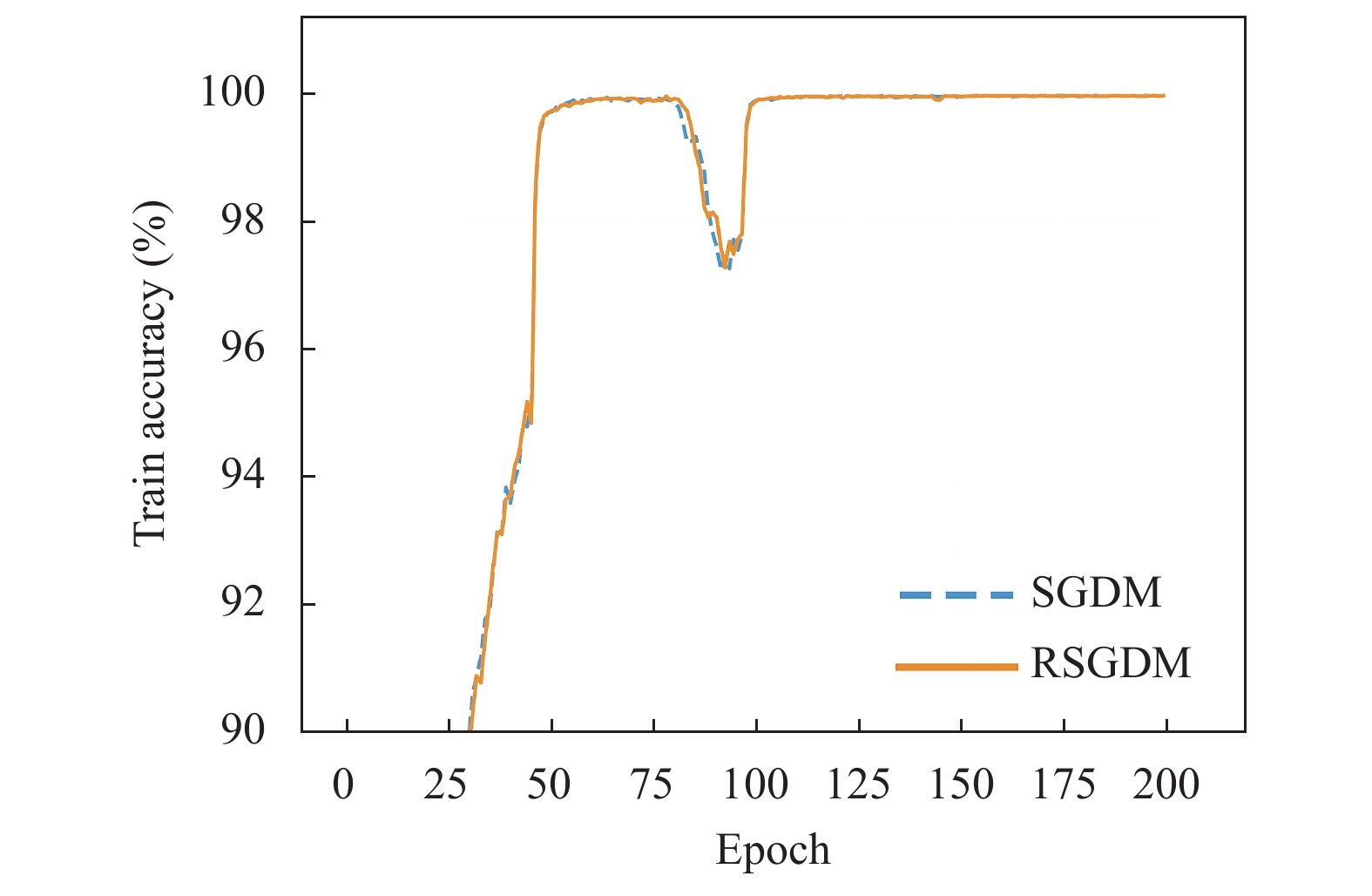
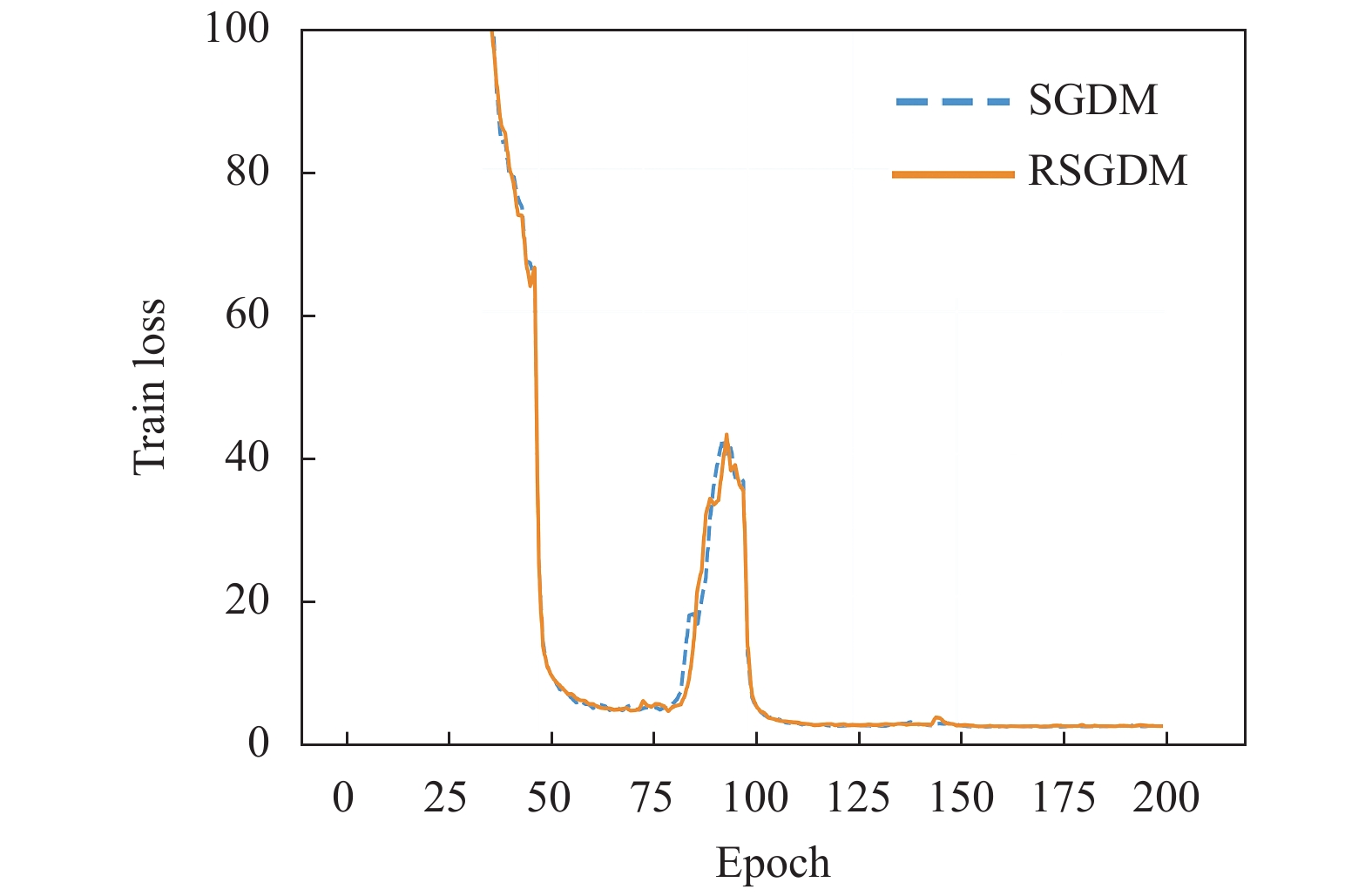
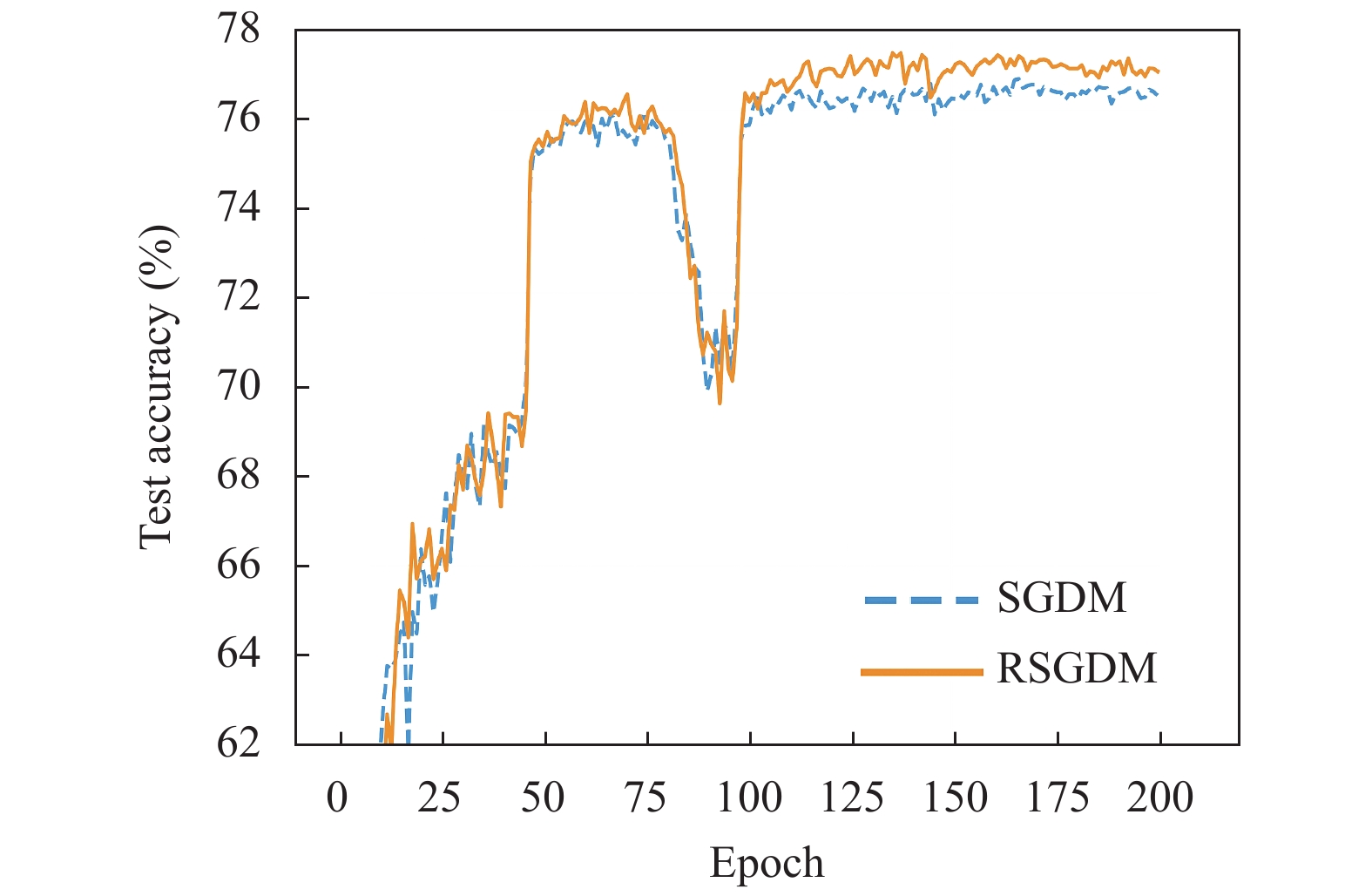
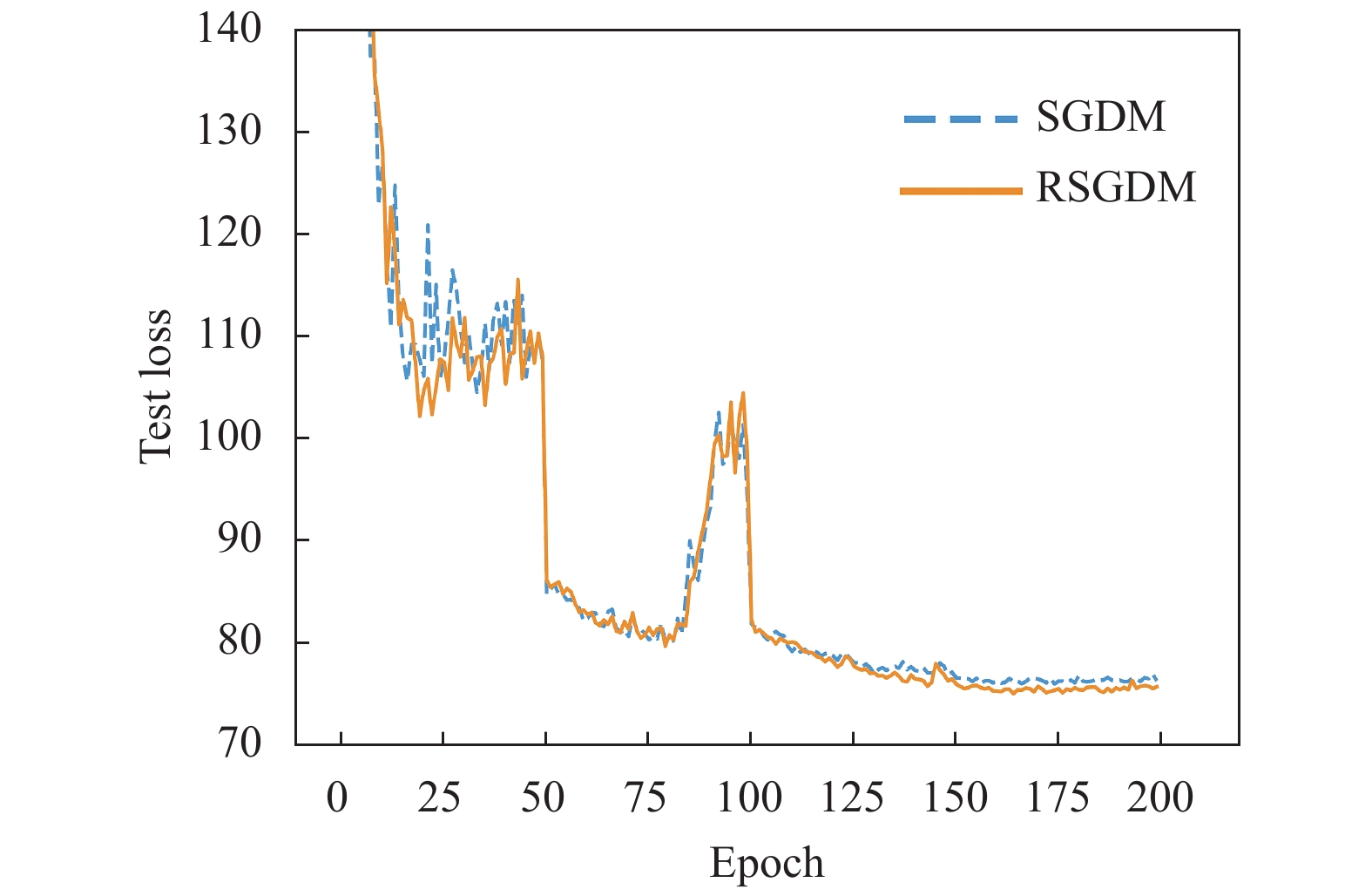
图5–图8给出了ResNet50在CIFAR-100上使用RSGDM算法和SGDM算法的实验结果. 可以得出与CIFAR-10类似的结果, 在训练准确率和训练损失上二者的几乎相同, 但是在收敛精度上, RSGDM算法的表现在这个数据集上要领先SGDM算法很多, 可以看测试准确率那张图, 从100个epoch之后, 我们的RSGDM方法始终准确率高于SGDM, 并且最终准确率比SGDM高了0.57%. 这进一步说明我们的方法是有效的.
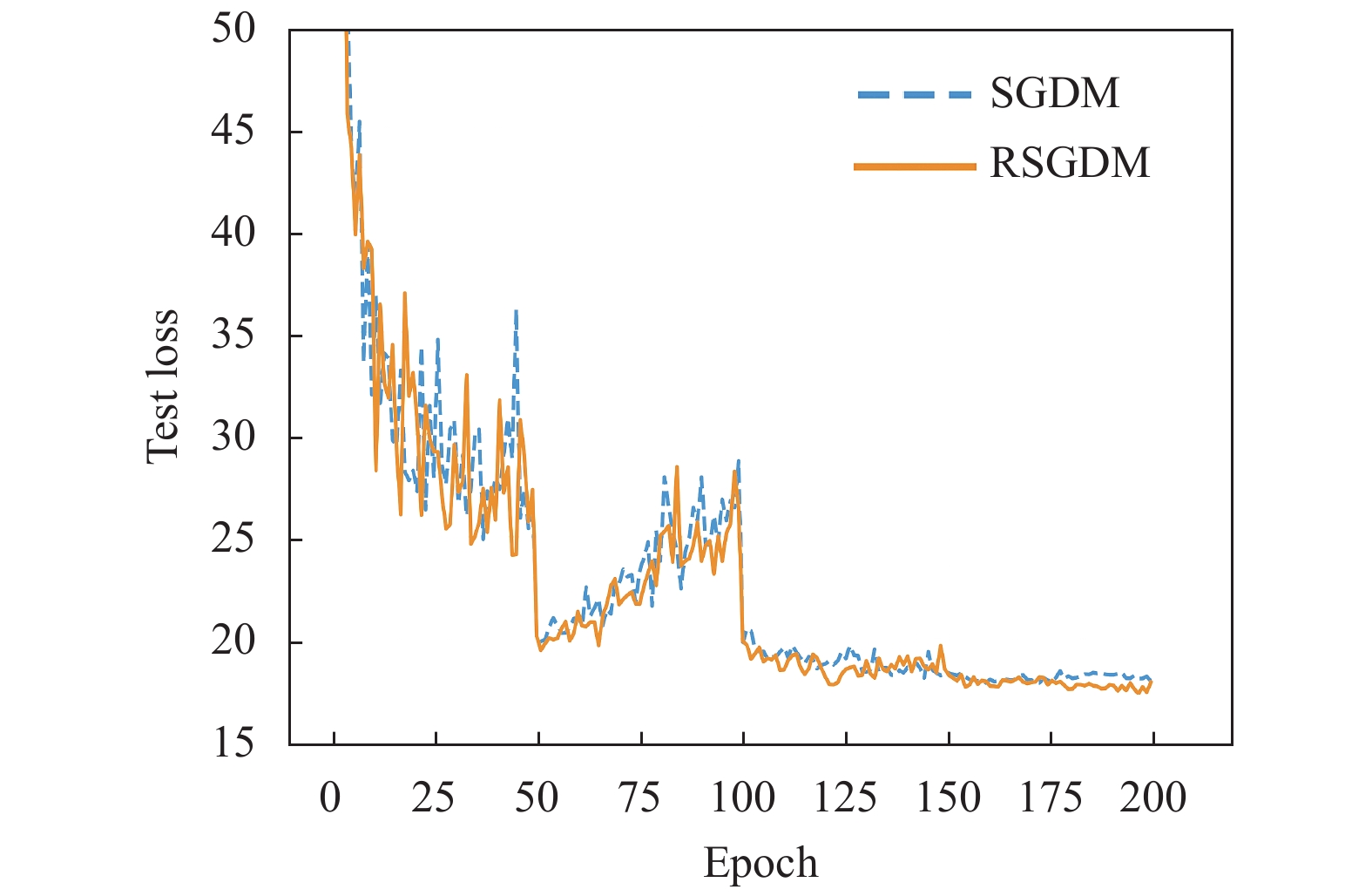
|
图 4 ResNet18在CIFAR-10上的测试损失 |
|
图 5 ResNet50在CIFAR-100上的训练准确率 |
|
图 6 ResNet50在CIFAR-100上的训练损失 |
4 结论
随着深度学习模型的不断复杂化, 训练一个精度高的模型越来越不容易, 一个好的优化器具有非常重要的作用. 本文分析了传统方法SGDM算法使用指数滑动平均估计总体梯度带来的偏差与滞后性, 并理论上证明了这个偏差与滞后性存在. 我们提出了基于差分修正的RSGDM算法, 该算法对梯度的差分进行估计并使用这个估计项修正指数滑动平均对梯度的估计, 我们从理论上说明了算法的可行性, 并且在CIFAR-10和CIFAR-100两个数据集上进行图像分类任务的实验, 实验结果也进一步说明了我们的RSGDM算法的优势. 值得一提的是, 我们的RSGDM算法没有引入更多的需要调试的参数, 在不加重深度学习研究员调试超参负担的情况下, 提升了收敛精度. 本文开头介绍了当前这个领域的其他方法, 包括现在最常用的学习率自适应性算法Adam等, 未来我们会使用现在的改进思路去提出新的学习率自适应性算法, 提出更加准确高效的算法.
|
图 7 ResNet50在CIFAR-100上的测试准确率 |
|
图 8 ResNet50在CIFAR-100上的测试损失 |
| [1] |
Ren SQ, He KM, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, QC, Canada. 2015. 91–99.
|
| [2] |
Cho K, van Merrienboer B, Gülçehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Proceedings of the 2014 Conference on Empirocal Methods in Natural Language Processing (EMNLP). Doha, Qatar. 2014. 1724–1734.
|
| [3] |
Xiong W, Droppo J, Huang X, et al. Achieving human parity in conversational speech recognition. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2017, 25(12): 2410–2423.
|
| [4] |
Robbins H, Monro S. A stochastic approximation method. The Annals of Mathematical Statistics, 1951, 22: 400-407. DOI:10.1214/aoms/1177729586 |
| [5] |
Sutskever I, Martens J, Dahl G, et al. On the importance of initialization and momentum in deep learning. Proceedings of the 30th International Conference on International Conference on Machine Learning. Atlanta, GA, USA. 2013. 1139–1147.
|
| [6] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 2011, 12: 2121-2159. |
| [7] |
Tieleman T, Hinton G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning, 2012, 4(2): 26-31. |
| [8] |
Zeiler MD. ADADELTA: An adaptive learning rate method. arXiv preprint arXiv: 12125701, 2012.
|
| [9] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the International Conference on Learning Representations. 2015.
|
| [10] |
Reddi SJ, Kale S, Kumar S. On the convergence of adam and beyond. Proceedings of the International Conference on Learning Representations. 2018.
|
| [11] |
Liu LY, Jiang HM, He PC, et al. On the variance of the adaptive learning rate and beyond. Proceedings of the International Conference on Learning Representations 2020. Addis Ababa, Ethiopia. 2020. 1–13.
|
| [12] |
Krizhevsky A. Learning multiple layers of features from tiny images. Toronto: University of Toronto, 2009.
|
| [13] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. 2016. 770–778.
|
 2021, Vol. 30
2021, Vol. 30



