长时间运行的软件系统, 会出现软件错误不断累积、占用资源不断增加、性能持续下降, 最终导致软件失效或崩溃的软件老化现象[1]. 对于发生老化的软件系统, 在适当时刻主动进行抗衰操作可以避免软件发生失效[2]. 因此, 如果能够实时准确预测软件系统的剩余寿命, 通过预测软件剩余使用寿命来推导软件最优抗衰时刻, 将会减少抗衰决策判断误差.
软件剩余使用寿命(Remaining Useful Life, RUL)指软件以当前的运行条件, 能够实现其正常功能的剩余时间[3]. RUL常见的预测方法可分为基于模型与数据驱动的方法. 基于模型的方法是指通过构建设备退化的数学或物理模型来进行预测. 马波等人提出了一种基于状态监测信息和滚动轴承退化物理模型的寿命预测方法[4].基于模型的方法取得了不错的效果, 但它依赖与特定的模型, 不利于推广[5].
数据驱动中的深度学习方法由于具有强大的数据驱动能力, 并且无需知道确切的物理模型和领域知识, 以及在非线性映射特征提取方面的优异性能, 成为了剩余寿命预测领域中热门方法[6]. 闫楚良等人[7]和王佳炜等人[8]用BP神经网络分别对材料疲劳寿命和电磁继电器进行了预测. Felix等人提出用循环神经网络(Recurement Netural Network, RNN)对航空发动机领域剩余寿命进行了预测[9]. RNN网络在结构设计中引入了时序的概念, 在学习具有内在依赖性的时序数据时能够产生对过去数据的记忆状态, 能够从原始数据获取更多的数据规律性特征. LSTM (Long Short-Term Memory)作为一种改进后的RNN网络, 成为剩余寿命预测的热点技术. 在航天发动机、锂电池、滚动轴承等剩余寿命预测领域都取得了成功[10-12].
基于上述分析, 本文提出了一种基于LSTM的Web软件系统实时剩余寿命预测模型, 该模型充分考虑了Web软件系统资源消耗的时间特性, 将当前系统的剩余寿命动态地与Web资源损耗情况相关联.
1 模型原理 1.1 长短期记忆网络LSTM是一种改进之后的循环神经网络, 可以解决RNN感知能力下降的问题[13]. 与RNN相比, LSTM在其基础上增加了一个细胞状态(cell state), 内部有4个网络层. 一个典型的LSTM通过3个门来控制细胞状态, 这3个门分别为遗忘门、输入门和输出门. 如图 1所示. 门控循环单元(Gate Recurrent Unit, GRU)是LSTM网络的一种变体, 它组合了遗忘门和输入门到一个单独的“更新门”中, 合并了细胞状态和隐藏状态, 没有输出门, 增加了重置门, 如图2所示.
LSTM三个门基于Sigmoid函数来增加或删除细胞状态中的信息, 其中遗忘门和控制门用来控制上一时刻细胞状态
| $\left\{ \begin{array}{l} {f_t} = {{Sigmoid}}({W_{hf}}{h_{t - 1}} + {W_{xf}}{x_t} + {{{b}}_{{f}}}) \\ {i_t} = {{Sigmoid}}({W_{hi}}{h_{t - 1}} + {W_{xi}}{x_t} + {{{b}}_{{i}}}) \\ {o_t} = {{Sigmoid}}({W_{ho}}{h_{t - 1}} + {W_{xo}}{x_t} + {{{b}}_{{o}}}) \\ {\widetilde c_t} = {\rm{tanh}}({W_{hc}} \cdot {h_{t - 1}} + {W_{xc}} \cdot {x_t} + {{{b}}_{{c}}}) \\ {c_t} = {f_t} \odot {c_{t - 1}} + {i_t} \odot \widetilde c{ _t} \\ {h_t} = {o_t} \odot \tanh ({c_t}) \\ \end{array} \right.$ | (1) |
式中, ft, it, ot ∈Rm分别表示遗忘门、输入门、输出门的计算结果;
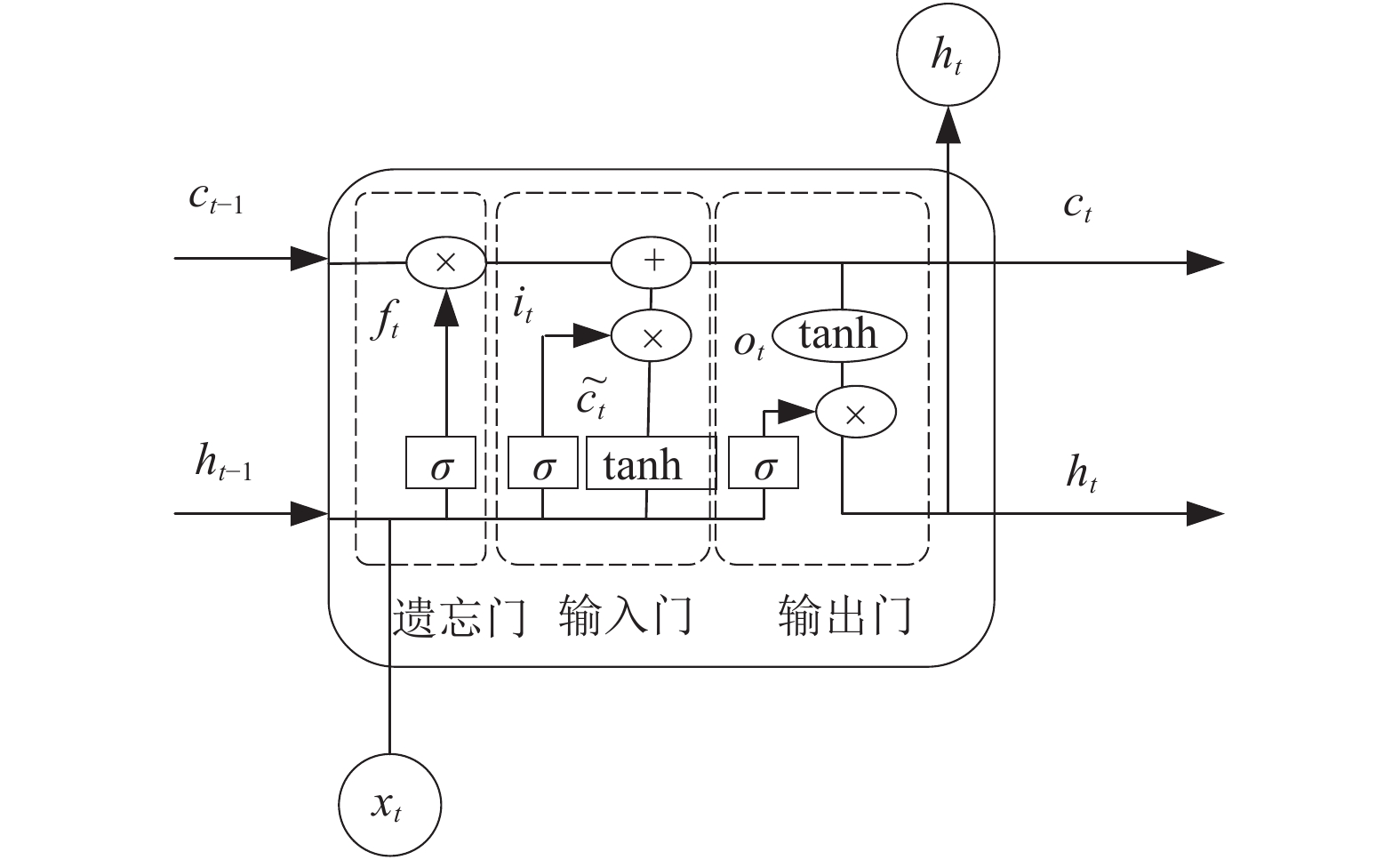
|
图 1 LSTM单元结构图 |
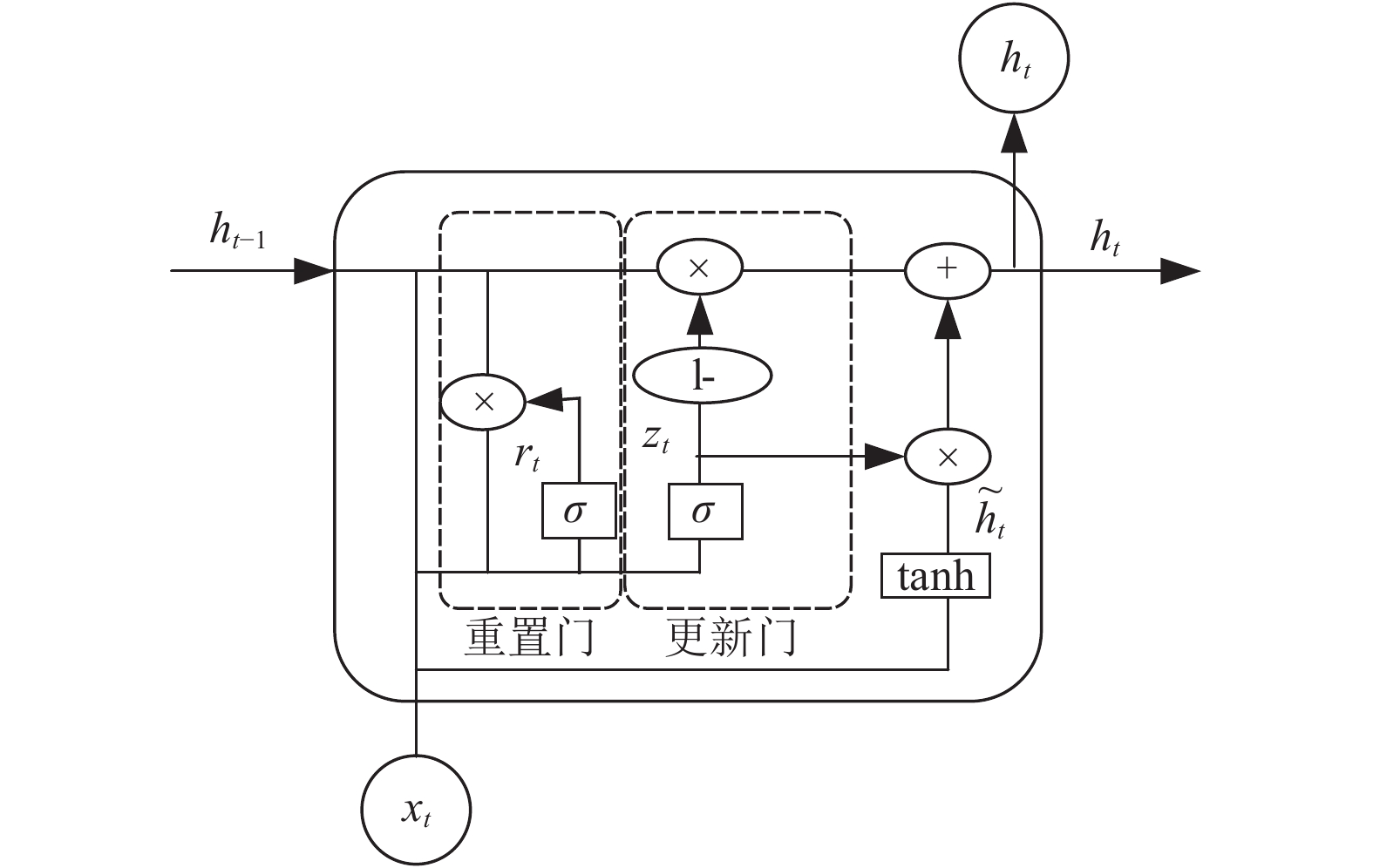
|
图 2 GRU单元结构图 |
1.2 基于LSTM网络的Web系统寿命预测模型构建过程
基于LSTM剩余寿命预测模型由输入层、两层LSTM层、池化层、全连接层、输出层构成. 如图3所示.
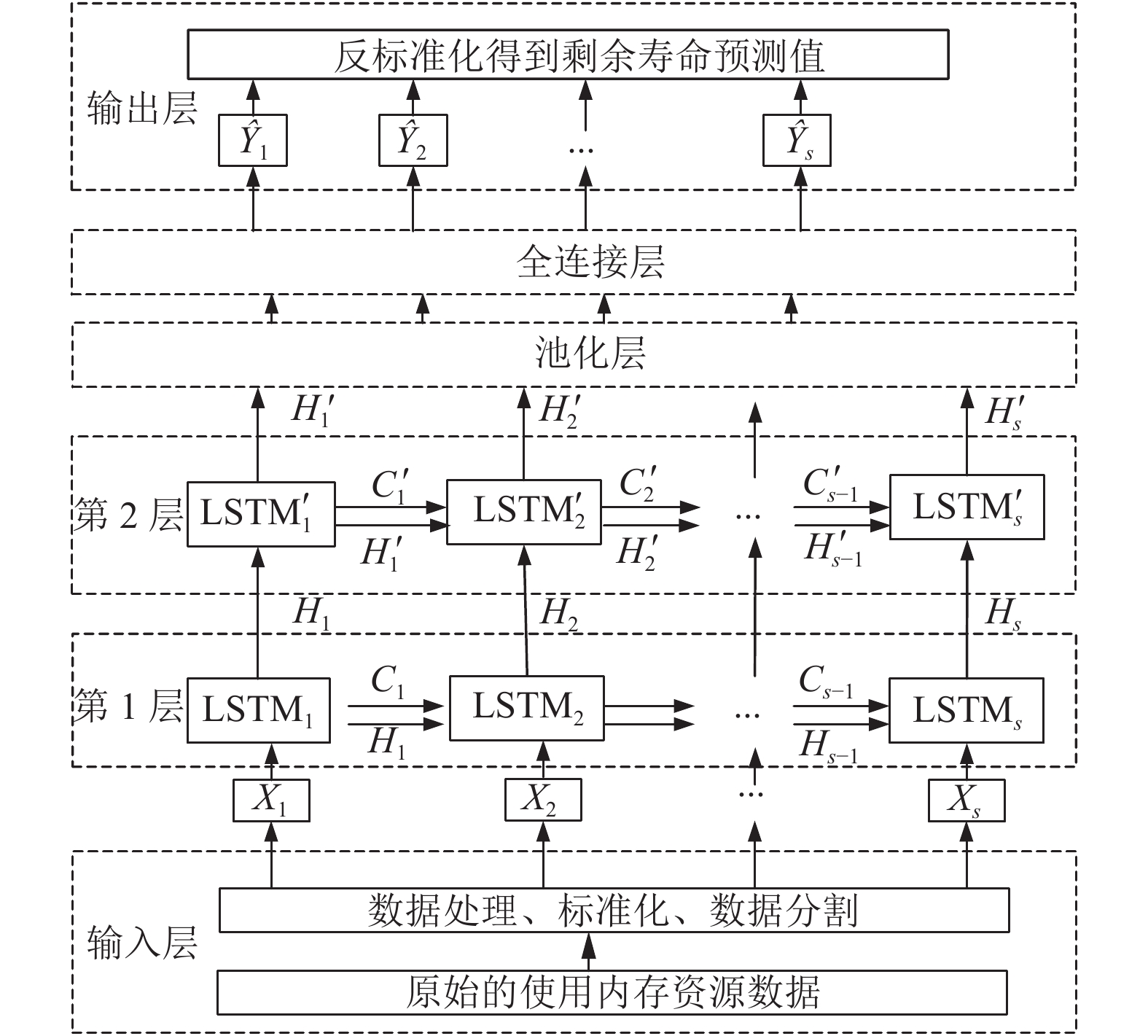
|
图 3 模型结构图 |
(1)收集样本并进行标准化处理
每秒收集一次Web软件系统运行过程内存使用量数据, 假设第n秒发上了OOM (Out Of Memory)故障, 则一共收集了n秒的系统运行数据. OOM指的是当系统因为没有足够的内存为对象分配空间, 就会报出这种故障. 将系统在第i秒的内存使用量表示为mi, 则系统在i秒的剩余寿命可表示为
| $(M,R) = \left\{ {\begin{array}{l} {\{ ({m_i},n - k)\} ,\;i = 1,2,3,\cdots,k } \\ {\{ ({m_i},{r_i})\} ,\;i = k + {\rm{1}},k + {\rm{2}},k + {\rm{3}},\cdots,n} \end{array}} \right.$ | (2) |
得到的样本表示为
| $\left\{ {\begin{array}{l} { {m_i}' = ({m_i} - \mathop {\min \{ {m_t}\} }\limits_{1 \le t \le n} )/(\mathop {\max \{ {m_t}\} }\limits_{1 \le t \le n} - \mathop {\min \{ {m_t}\} }\limits_{1 \le t \le n} )} \\ {{r_i}' = ({r_i} - \mathop {\min \{ {r_t}\} }\limits_{1 \le t \le n} )/(\mathop {\max \{ {r_t}\} }\limits_{1 \le t \le n} - \mathop {\min \{ {r_t}\} }\limits_{1 \le t \le n} )} \end{array}} \right.$ | (3) |
(2)按照时间步长得到模型的输入
将集合
| $\left\{ {\begin{array}{*{20}{c}} {(X,Y) = \{ ({X_i},{Y_i}),i = 1,2,3,\cdots,n - w\} } \\ {{X_i} = \{ m_i',m_{i + 1,}'\cdots,m_{i + w}'\} ,{Y_i} = r_{i + w}'\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right.$ | (4) |
(3)确定LSTM的网络结构并初始化网络
确定网络的时间步长、隐含层单元数、每层网络节点的舍弃率以及相应的激活函数、误差的计算方式和权重更新迭代方式. 给定初始权值矩阵, 设置最大迭代次数和最小误差值, 训练网络以更新各项网络参数.
(4)前向计算
将
| $\left\{ {\begin{array}{*{20}{c}} {\hat Y = \{ {{\hat Y}_{1,}}{{\hat Y}_2},\cdots,{{\hat Y}_i},\cdots,{{\hat Y}_{n - w}}\} } \\ {{{\hat Y}_i} = LST{M_f}\{ {X_{i,}}{C_{i - 1}},{H_{i - w}}\} } \end{array}} \right.$ | (5) |
(5)池化层和全连接层
池化层将经过LSTM层处理输出的
(6)定义损失函数
损失函数的计算公式如式(6)所示, 式中, n为测试样本总数,
| $loss = \frac{1}{{n - w}}\sum\limits_{i = 1}^{n - w} {({{\hat Y}_i} - {Y_i}} {)^2}$ | (6) |
(7)反向误差传播
采用批量梯度下降算法对指标数据进行批次划分, 采用优化算法(RMSprop、AdaDelta、Adamax、Adam)对当前的损失函数进行优化, 实时调整网络的偏置和权值, 使网络误差不断减少. 当最小误差和迭代次数满足要求时停止训练模型. 将测试样本数据输入模型得到预测结果.
(8) 评价指标
为评估基于LSTM网络的Web寿命预测模型的性能, 用平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Squared Error, RMSE)作为评价指标. 其公式如下:
| $d = \hat Y - Y$ | (7) |
| $MAE = \frac{1}{n}\sum\limits_{{d_i} \in {{d}}} {|{d_i}|} $ | (8) |
| $RMSE = \sqrt {\frac{1}{{{n}}}\sum\limits_{{d_i} \in {{d}}} {{d_i}^2} } $ | (9) |
除了RMSE和MAE之外, 本文引入另外两个相对评价指标: 指数评价函数(Scoring Function, SF)和相对准确率(Accuracy). 预测寿命相对剩余寿命偏小和偏大, 分别设置不同的影响因子, 分别记做a1和a2, 且a1>a2, 这是因为比起Web失效后采取抗衰操作, 在失效之前执行抗衰操作带来较小的损失. 本文中影响因子设为a1=150, a2=50.
| $H({d_i}) = \left\{ {\begin{array}{l} {{{\rm e}^{ - {d_i}/{a_1}}} \;\;\;\; {d_i} \le 0} \\ {{{\rm e}^{{d_i}/{a_{\rm{2}}}}} \;\;\; {d_i} > 0} \end{array}} \right.$ | (10) |
| $SF = \frac{{\displaystyle\sum\limits_{{d_i} \in {{d}}} {H({d_i})} }}{n}$ | (11) |
| $I({d_i}) = \left\{ {\begin{array}{l} {1, \;\;\; - {a_1} \le d \le {a_2}} \\ {0,\;{\rm {otherwise}} } \end{array}} \right.$ | (12) |
| $Accuracy = \frac{{\displaystyle\sum\limits_{{d_i} \in {{d}}} {I({d_i})} }}{{{n}}} \times 100{\text{%}}$ | (13) |
由于软件老化是一个错误不断累计的过程, Web软件系统开始出现老化后并不会立刻失效, 需要耗费很长时间才会发现故障. 受Matias等人提出的系统化方法的启发[14], 本文仿照工业领域应用的加速理论, 在Web软件系统中采用加速内存泄露的方法收集可以反映软件老化情况的指标数据, 基于收集到的时序数据, 构建基于LSTM的Web软件系统实时剩余寿命预测模型.
2.1 数据收集为收集因内存泄露导致的软件老化的指标数据, 搭建了一个符合多层TPC-W基准测试规范的电子商务网站购书系统. 该软件系统由一个Web服务器, 一个数据库服务器和一组模拟的客户端组成. 三者之间的关系如图4所示, Web服务器Tomcat关于JVM的内存配置参数如表1所示.
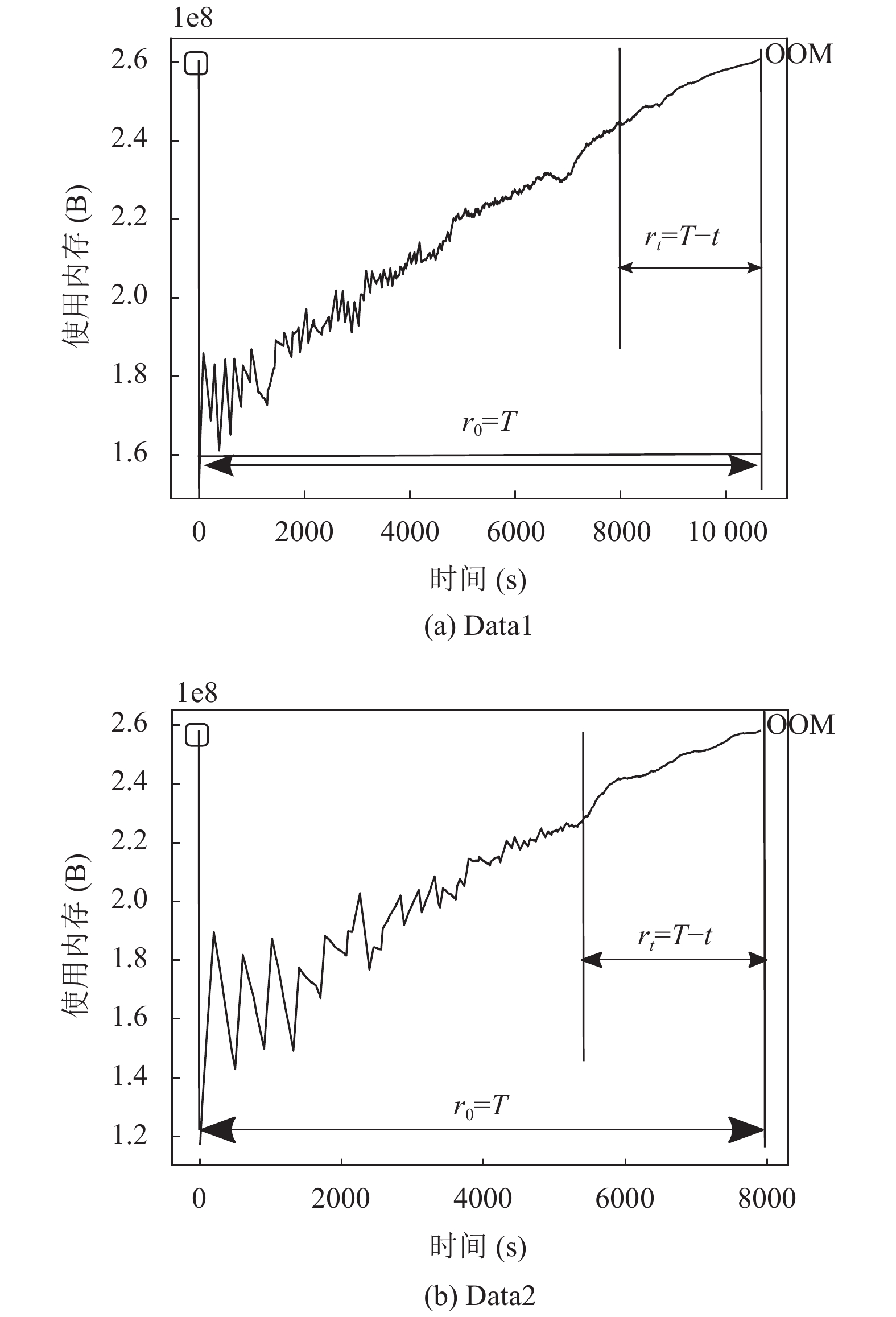
设定服务端的内存泄漏强度和客户端并发数, 运行该系统直到发生OOM故障为一次实验. 当发生OOM故障时, 记当前时刻为T, 该时刻系统剩余寿命r=0. 实验过程中每1 s收集一次JVM的内存使用量, 采集到的样本个数分别为10929, 8202. 如图 5所示, 表示Web系统在不同内存泄露强度(leakage)和客户端并发数(concurrency)下的内存变化趋势图. 表2为数据对应的实验参数.
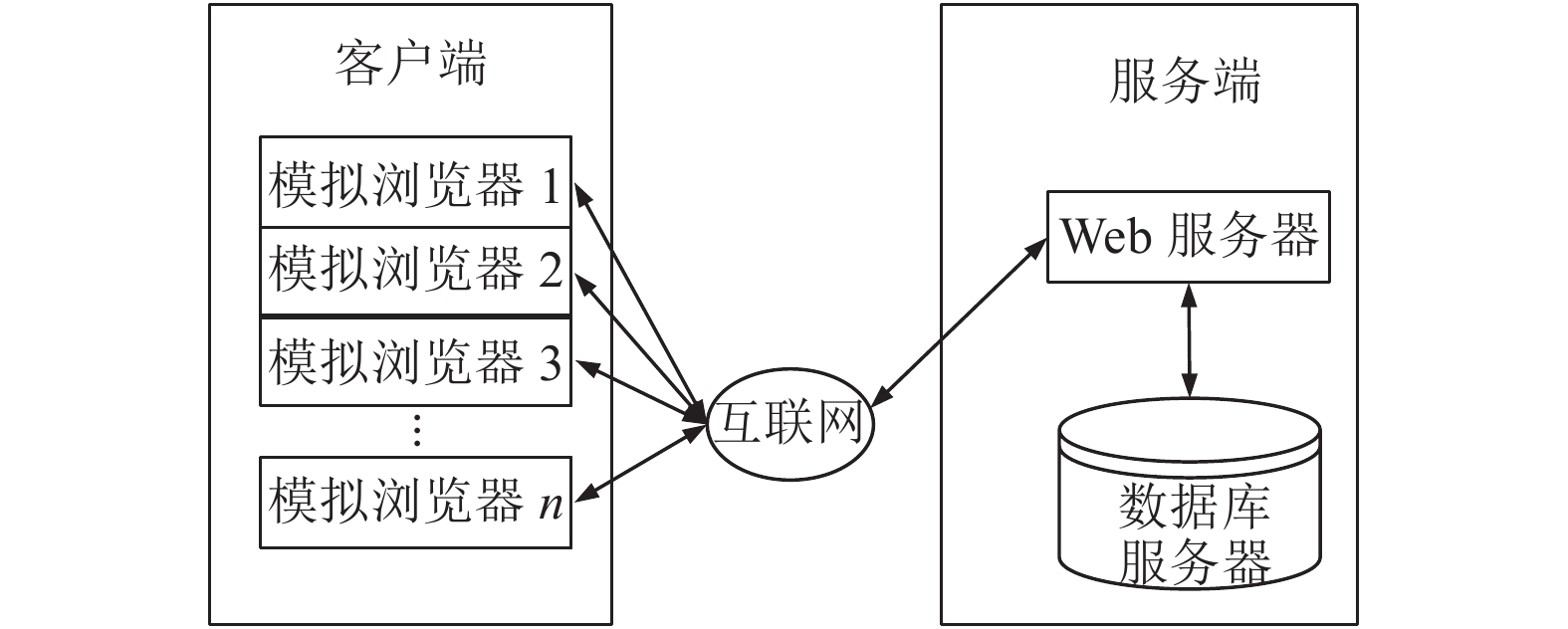
|
图 4 三者间的工作原理 |
| 表 1 Tomcat关于JVM堆内存配置信息 |
|
图 5 JVM内存使用情况变化趋势图 |
| 表 2 实验运行参数 |
2.2 实验环境 2.3 基于LSTM的剩余寿命预测模型
实验环境参数如表3. 本文使用Keras框架搭建并训练LSTM网络预测模型, 所使用到的网络主要由循环层(recurrent)中的LSTM层和全连接层(dense)组成. 用Data1作为训练集, 其余3组作为测试集. 分别比较不同优化算法、隐含层单元数下的模型性能. 最后在相同参数情况下, 与RNN、GRU模型结构进行对比.
(1)寻找合适的隐含层单元数量
用Data2做测试集, 用Adam算法进行优化, MAE作为评价指标, 尝试不同隐含层单元数量寻找最佳的网络结构. 结果如表4所示, 可以看出隐含层单元数量为120时, MAE的值最小.
| 表 3 实验环境参数 |
| 表 4 不同隐含层单元数量的MAE |
(2)优化算法
在隐含层单元数为80情况下, 用Data2做测试集, 采用不同的优化算法训练模型, 用MAE作为评价指标. 对比不同算法在训练集和测试集上MAE的大小. 结果如表5 所示, 可以看出Adam的算法的性能优于其它算法.
| 表 5 不同优化算法的MAE对比 |
(3)与单层LSTM网络进行对比
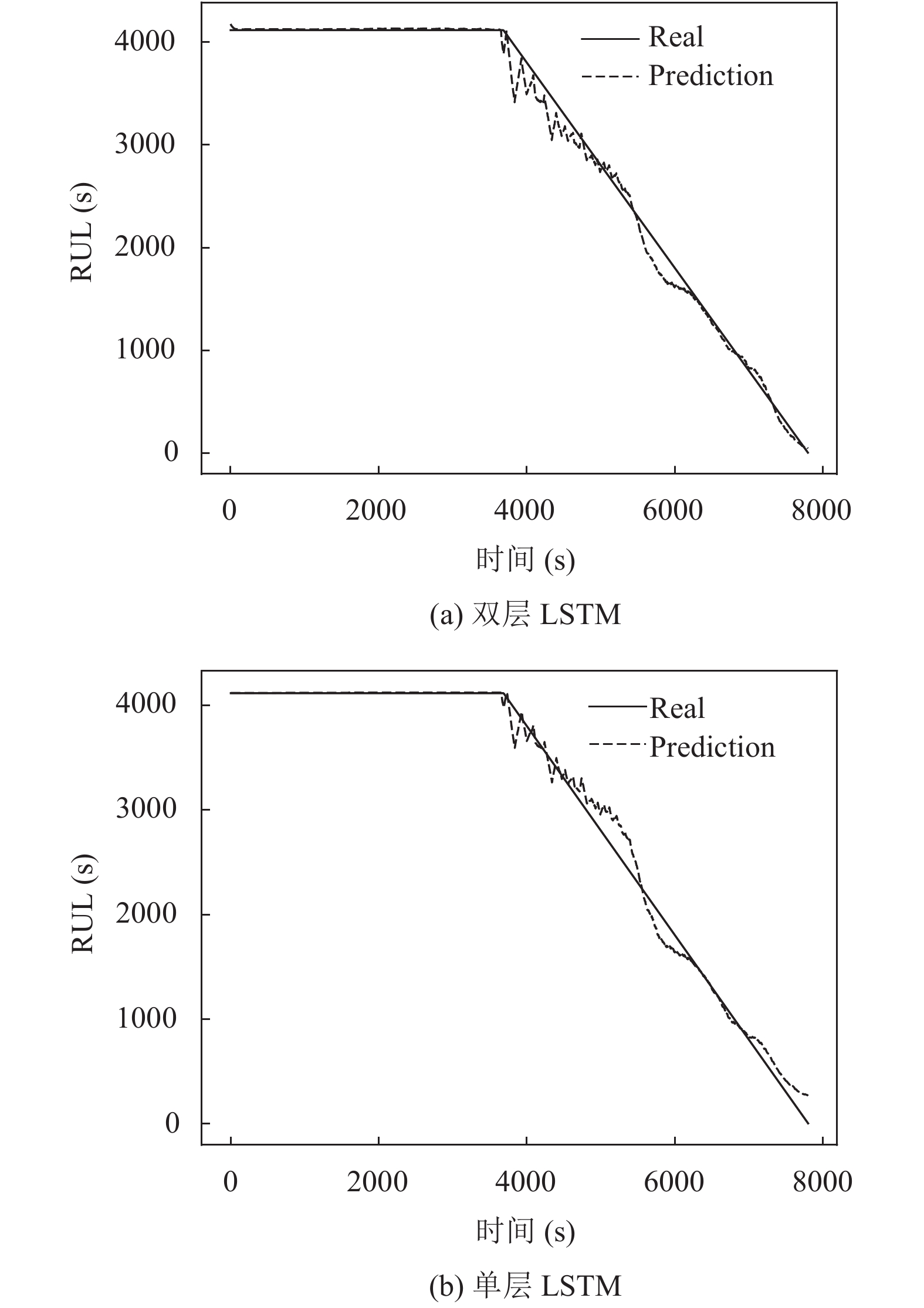
为了验证基于LSTM网络的Web软件系统剩余寿命预测模型的优势, 用Adam优化算法、隐含层单元数量为120的参数下, 将双层LSTM网络的结构与单层的LSTM网络结构做了对比. 从图6可以看出, 双层LSTM网络结构的拟合效果更好, 用MAE和SF作为评价指标, 对比两种网络的性能. 如表6所示, 可以看出双层的LSTM网络结构相较于单层的LSTM网络结构性能有所提升.
|
图 6 寿命预测结果对比图 |
| 表 6 网络性能对比 |
2.4 结果分析
第2.3节实验验证了基于神经网络RNN以及LSTM的Web软件系统剩余寿命预测模型的适用性. 而从表6可看出, 改进后的基于LSTM寿命预测模型对于Web软件系统抗衰决策具有良好指导意义. 为了进一步验证改进后的基于LSTM寿命预测模型的预测能力, 表7列出了各网络模型在不同指标下的评价指标对比, 表中PT (Prediciton Time)表示单位样本预测所需要的时间, 单位为ms, 从表中可以看出, PT值较小, 满足实时预测要求. 从表中可以看出, 改进后LSTM寿命预测模型在3组实验里的MAE、RMSE、SF都是最低, Accuracy最高, 说明该寿命预测相较与BP网络和常规循环神经网络而言, 预测精度最高.
| 表 7 各网络预测精度对比 |
3 结论
本文通过搭建引入内存泄露的软件老化实验平台收集能够反映软件老化的指标数据, 根据获取到的性能指标数据构建并训练了基于LSTM的Web软件系统实时剩余寿命预测模型. 通过实验表明该预测模型与Web软件系统的寿命趋势一致, 拟合度很高, 能够准确地预测软件的剩余寿命, 为及时采取老化软件的抗衰决策提供保证. 与常规循环神经网络和BP网络相比, 满足实时性要求, 预测精度高. 说明LSTM网络能够完成Web软件系统实时剩余寿命预测的要求.
| [1] |
Wu XX, Zheng W, Pu MC, et al. Invalid bug reports complicate the software aging situation. Software Quality Journal, 2020, 28(1): 195-200. DOI:10.1007/s11219-019-09481-2 |
| [2] |
Zheng JJ, Okamura H, Dohi T. A transient interval reliability analysis for software rejuvenation models with phase expansion. Software Quality Journal, 2020, 28(1): 173-194. DOI:10.1007/s11219-019-09458-1 |
| [3] |
陈自强. 基于LSTM网络的设备健康状况评估与剩余寿命预测方法的研究[硕士学位论文]. 合肥: 中国科学技术大学, 2019.
|
| [4] |
马波, 翟斌, 彭琦, 等. 基于不同退化阶段状态空间模型及粒子滤波的滚动轴承寿命预测. 北京化工大学学报(自然科学版), 2017, 44(3): 81-86. |
| [5] |
高彩霞, 吴彤, 付子义. 线性回归与EEMD的滚动轴承剩余寿命预测. 机械科学与技术, 2019, 38(10): 1589-1597. |
| [6] |
裴洪, 胡昌华, 司小胜, 等. 基于机器学习的设备剩余寿命预测方法综述. 机械工程学报, 2019, 55(8): 1-13. |
| [7] |
闫楚良, 郝云霄, 刘克格. 基于遗传算法优化的BP神经网络的材料疲劳寿命预测. 吉林大学学报(工学版), 2014, 44(6): 1710-1715. |
| [8] |
王佳炜, 王召斌, 黄周霖. 果蝇算法优化的BP神经网络在电磁继电器贮存寿命预测中的应用. 电器与能效管理技术, 2019(2): 19-24. DOI:10.3969/j.issn.1001-5531.2019.02.005 |
| [9] |
Heimes FO. Recurrent neural networks for remaining useful life estimation. Proceedings of 2008 International Conference on Prognostics and Health Management. Denver, CO, USA. 2008. 1–6.
|
| [10] |
Wu YT, Yuan M, Dong SP, et al. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing, 2018, 275: 167-179. DOI:10.1016/j.neucom.2017.05.063 |
| [11] |
胡天中, 余建波. 基于多尺度分解和深度学习的锂电池寿命预测. 浙江大学学报(工学版), 2019, 53(10): 1852-1864. DOI:10.3785/j.issn.1008-973X.2019.10.002 |
| [12] |
王奉涛, 刘晓飞, 邓刚, 等. 基于长短期记忆网络的滚动轴承寿命预测方法. 振动、测试与诊断, 2020, 40(2): 303-309. DOI:10.16450/j.cnki.issn.1004-6801.2020.02.013 |
| [13] |
Sak H, Senior A, Beaufays F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv: 1402.1128, 2014.
|
| [14] |
Zhao J, Jin YL, Trivedi KS, et al. Software rejuvenation scheduling using accelerated life testing. ACM Journal on Emerging Technologies in Computing Systems, 2014, 10(1): 9. DOI:10.1145/2539118 |
 2021, Vol. 30
2021, Vol. 30



