兴趣点(Point-Of-Interest, POI)推荐是个性化推荐方向中的一个分支, 其目的在于根据用户访问兴趣点的轨迹日志以及两者本身的特征, 为用户推荐符合其偏好的兴趣点[1]. 在基于位置的社交网络(Location-Based Social Networks, LBSN)中, 用户通过移动设备上的应用在附近的兴趣点签到, 从而分享自己所处的位置, 以生成属于自己的兴趣点行为轨迹. 而兴趣点推荐算法从某种意义上讲, 是基于用户在LBSN中的轨迹所研究或改进的一种面向兴趣点的推荐算法.
目前为止, 兴趣点推荐相关的研究主要以用户的兴趣点访问序列、访问频次以及用户本身所具有的社会关系网为基准进行推荐. 其中, 基于序列的推荐方法对兴趣点访问序列进行时空上下文信息的挖掘, 从而推测出用户在下一时刻可能将要访问的兴趣点. 基于访问频次的兴趣点推荐方法则是将用户在LBSN中所产生的签到数据转化为用户-兴趣点矩阵, 其元素为用户对该兴趣点的总共访问次数, 从而将兴趣点推荐任务转化为一般的用户-物品矩阵的空缺项填充任务(即矩阵分解). 而基于社交关系网的推荐方法则是根据用户关系网所延展到的其它用户信息, 以及用户之间的访问轨迹相似度, 为用户进行推荐.
在基于访问频次的兴趣点推荐方法中, 针对用户未访问过的兴趣点, 其偏好程度能够被有效地预测出来. 然而该方法没有考虑到用户本身和兴趣点的地理位置关系, 以及用户签到数据的时间关系. 同理, 基于社交关系网的推荐方法将用户相似度的计算过程以关系网数据进行强化, 从而使相似用户的推理以及兴趣点的推荐更具有合理性, 但同样没有考虑到用户偏好的时空上下文关系. 因此, 基于序列和时空上下文信息的方法适用于兴趣点访问序列的推荐, 以局部的角度来讲, 此方法最有可能实现低访问代价下用户对偏好兴趣点的访问需求, 但其推荐的产生方式类似于贪心算法, 即根据前n项的兴趣点访问记录生成用户下一个最有可能访问且代价相对较小的兴趣点. 在不强调兴趣点访问顺序以及特定访问(必须经过的)兴趣点的情况下, 局部访问代价最小不全等于全局访问代价最小. 图1为理想状态下兴趣点的推荐结果.
基于上述兴趣点推荐的相关研究可以发现, 大部分的兴趣点推荐研究成果将LBSN的信息作为用户喜好的参考进行推荐, 完全没有考虑到用户是否有必要访问最符合喜好的兴趣点, 以及访问兴趣点所付出的距离代价. 而另外一小部分的研究成果虽然考虑到了兴趣点的地理位置以及距离关系为用户进行推荐, 但究其细节, 很难做到以全局最优为考量满足低访问代价下用户对偏好兴趣点的访问需求. 因此, 针对上述问题, 本文提出了一种基于序列挖掘与距离损失优化的兴趣点推荐方法. 其中, 序列挖掘的目的在于通过用户的兴趣点访问历史序列总结出用户所感兴趣的兴趣点特征, 而距离损失优化的目的在于使兴趣点序列所产生的整体访问代价达到最小.

|
图 1 兴趣点推荐示例 |
2 相关工作
如引言所述, 许多兴趣点推荐相关的研究基于LBSN的信息对兴趣点的推荐序列进行优化, 力求所生成的兴趣点候选项能够尽可能地符合用户的偏好. 其中, 一部分基于协同过滤的算法以LBSN中的签到数据为基准对用户的兴趣点偏好进行预测. 例如文献[2]中所提出的模型, 将用户与兴趣点之间产生的交互数据转化为矩阵, 以矩阵分解的形式预测用户对未曾到达过的地点的偏好程度.
相当一部分融合社交关系信息优化矩阵分解的方法以直接相连的用户间关系为基准对算法模型进行优化. 在实际的应用场景中, 具有直接关系的用户被认为具有相似的偏好, 因此可以当作推荐的依据. 基于此, 以社交关系信息与评分信息相结合的推荐模型成为主流, 如Ma等所提出的SoRec模型[3]以及Guo等所提出的TrustSVD算法[4]. 此外, 在文献[4]的工作中, 用户间的直接社交关系以及评分信息被整合为一个混合矩阵, 基于该混合矩阵, Guo等提出了基于随机梯度下降的分解算法.
然而, 所有基于协同过滤的推荐算法具有一定的共性, 即侧重于用户对项目所产生的交互值(如评分)而非用户或项目本身, 因此该算法无法充分运用兴趣点或用户本身的信息完善其推荐性能. 并且, 在现实世界中, 用户的兴趣点访问轨迹重合率较低, 因此对于协同过滤相关的算法, 其性能将受到数据稀疏性的制约. 针对此类问题, 许多有关协同过滤的研究成果以用户-项目交互值之外的信息作为补充, 避免数据稀疏性带来的负面影响.
在基于LBSN的信息中, 用户的兴趣点访问轨迹以及兴趣点的地理位置也是推荐算法的重要考虑因素. 在龚卫华等[5]提出的基于社区发现的兴趣点推荐方法中, 兴趣点按照地理位置被归类为多个簇, 根据多个簇所凸显出的喜好特征, 用户相对于地理位置簇的隶属度(即喜好程度)被计算出来, 从而由面及点, 将隶属度高的地理位置簇中的兴趣点推选给相应的用户. 基于社区发现的方法侧重于利用用户本身所携带的社区关系网以及兴趣点位置为用户生成兴趣点候选项, 充分利用LBSN中的信息进行推荐. 但此方法将兴趣点地理位置作为偏好因素为用户生成推荐列表, 并没有将兴趣点地理位置所隐含的访问距离代价考虑在内, 在兴趣点次序以及必要性需求较弱的情况下, 所推荐的兴趣点序列可能脱离用户的实际要求.
序列推荐是推荐算法的一个子集, 其目的在于以用户对物品产生的交互作为历史依据, 为用户生成一系列符合其偏好的推荐候选序列. 在实际的应用中, 用户对物品的偏好可能会随着时间的推移产生变化, 因此有必要利用时空上下文相关的信息对推荐算法进行进一步优化. 考虑到上述问题, Koren等在矩阵分解的过程中所产生的偏置信息同时间变量建立映射关系, 提出timeSVD[6]模型. 但从现实意义上来讲, 用户兴趣与时间的映射关系因人而异, 简单的线性关系不能够完整准确地描述用户随时间推移产生的兴趣变化. 因此, 基于序列的推荐更偏向于对用户历史行为建模而非对用户兴趣与时间变量的映射关系建模.
针对推荐任务中用户交互序列所隐含的复杂时空上下文关系, RNN和CNN的思想也被应用于序列推荐中. Hidasi等针对大部分推荐系统只能根据短时的会话记录进行推荐, 而不能根据长时间的用户行为记录进行有效推荐的问题, 对传统RNN进行了修改, 使之更适应于序列化推荐[7]. Tang等提出CASER[8]模型, 这是一种基于CNN思想实现的推荐模型, 目的是来预测用户未来可能有交互行为的前n个物品的排序. 该模型的主要思想是将一系列最近产生交互的物品嵌入到时间和潜在空间所对应的“图像”中, 并使用卷积滤波器学习交互序列作为图像的局部特征.
在兴趣点推荐任务中, 用户的兴趣点访问序列具备完整的时空信息. 在蒋宗礼等[9]的研究成果中, 兴趣点推荐问题被转化为根据用户的历史访问序列预测未来兴趣点序列的问题. 在用户的兴趣点历史访问序列中, 兴趣点之间的转移概率, 即用户从其中一个兴趣点在若干步以内转移至下一个兴趣点的概率, 通过统计学的方式计算出来. 根据兴趣点之间的转移概率, 受到NLP领域中Skim-gram方法的启发, 以长文本中词预测的方式对用户将要访问的下一个兴趣点进行预测. 在强调兴趣点先后顺序的情况下, 本方法能够在局部意义上实现为用户推荐访问代价较小且符合习惯的兴趣点访问序列. 然而, 在现实环境中, 存在相对一部分用户, 其行为轨迹中对兴趣点的访问顺序并非如句子中的词向量一样具有明显的先后关系, 兴趣点之间的转移概率可能差别并不大. 因此从全局的角度来看, 此类方法不适用于这部分用户的兴趣点推荐.
此外, 在实际的应用中, 用户并不是在任何时候都对自己所经过的兴趣点信息实时上报. 在本文所使用的数据集中, LBSN信息仅仅包含用户之间简单的关系网以及兴趣点的访问轨迹, 并不包含交互类的附加信息(如评分或文本评价). 由于用户的行动距离有限, 用户之间的兴趣点轨迹重合程度普遍较低, 其数据稀疏性比一般的电商平台中的用户订单数据可能还要高, 针对未访问过的兴趣点不能单纯以用户相似度做出准确的喜好估计. 由此可见, 兴趣点推荐虽然是推荐领域中的一个分支, 但其所要考虑的因素比一般的推荐算法要广, 用户对兴趣点的偏好往往与用户的行动能力、兴趣点的相对距离以及用户本身的社交网(邻近用户的偏好)有关. 因此, 本文提出了一种兼顾用户偏好以及访问代价的兴趣点推荐方法, 旨在将上述信息进行整合, 为用户生成符合现实情况的兴趣点访问序列.
3 算法模型首先, 基于LBSN的兴趣点推荐任务可以表述如下: 设
针对上述推荐任务, 本文提出了如图2所示的算法模型. 该算法模型首先将用户与兴趣点的交互矩阵以社交关系信息进行补充, 之后对补充后所生成的混合矩阵进行分解. 最后, 根据用户对兴趣点的访问记录, 对矩阵分解的过程中所生成的兴趣点隐向量建立时序关系, 以类递归形式的模型对序列进行学习, 从而推断出用户将来可能访问的兴趣点.

|
图 2 模型结构 |
3.1 基于社交距离的混合矩阵
在兴趣点推荐的实际应用环境中, 根据访问频次所形成的用户-兴趣点交互矩阵往往表现出较高的稀疏性. 通过LBSN中给定的社交关系网, 交互矩阵得以稠密化, 为下一步的矩阵分解以及用户或兴趣点的隐特征向量生成做准备.
然而, 直接相连的社交关系对相似用户的喜好挖掘并不充分, 在现实世界中具有间接关系的用户之间也具有一定的联系. 考虑到LBSN中所提供信息的局限程度, 本文参考了文献[4]中的思想, 以用户之间的关系距离为参考, 将用户社交关系信息以及用户-兴趣点的交互信息整合为混合矩阵.
针对每一个用户
| $s(i,k) = \frac{1}{{1 + \min(d(i,k))}}$ | (1) |
其中,
根据用户间社交关系亲疏程度将矩阵稠密化的步骤可概括如下:
1)对于用户-兴趣点交互矩阵的每一行, 可看作用户
| ${u_i} = [{f_{i1}},{f_{i2}},\cdots,{f_{ij}},\cdots,{f_{im}}]$ | (2) |
2)对每一个用户
| $r{u_i} = \frac{{\displaystyle\sum\nolimits_{k = 0}^n {s(i,k){u_i}} }}{{\displaystyle\sum\nolimits_{k = 0}^n {s(i,k)} }}$ | (3) |
3)将每一个用户向量
至此, 原本的用户-兴趣点交互矩阵以用户关系网信息作为参考, 经过稠密化与标准化形成新的矩阵R, 对其进行矩阵分解, 可得到用户或兴趣点的隐特征向量表示.
3.2 带偏置项的矩阵分解在上一小节中, 融合用户社交关系以及兴趣点访问次数的混合矩阵已经构建完成, 依据SVD的思想, 考虑到偏置信息[10], 矩阵中的每一个元素可表示为:
| $\widehat {{r_{ij}}} = {p_i}q_j^{\rm{T}} + {b_i} + {b_j} + \mu $ | (4) |
其中,
| ${\cal L} = \sum\nolimits_{i,j} {\left( {{{\left( {\widehat {{r_{ij}}} - {r_{ij}}} \right)}^2} + \lambda \left( {||{p_i}|{|^2} + ||{q_j}|{|^2}} \right)} \right)} $ | (5) |
可以看出, 损失部分由两部分构成, 前者为预测值
为了充分利用用户的兴趣点访问序列中所隐含的上下文信息优化推荐性能, 将长短期记忆网络的思想应用于基于序列的推荐任务中. 长短期记忆网络(Long-Short Term Memory, LSTM)基于RNN改进, 是一种对时间序列所隐含的信息进行挖掘的模型, 能够有效避免序列元素的长依赖问题. 在本文所使用的Gowalla数据集中, 用户的兴趣点访问序列长度最多可达1600左右, 宜用LSTM进行处理.
根据Li等[11]的分析, 在实际的推荐任务中, 用户的决策过程受到其当前动机和长期偏好的影响. 针对两种不同的影响因素, Li等所提出的行为神经网络针对用户的短期访问行为和历史访问记录分别建立两种不同的LSTM进行学习, 最终以一个全连接网络将两种LSTM的输出进行汇总, 得到用户的下一项可能访问的物品. 以Li等所提出的算法模型作为参考, 本文对LSTM中的损失函数进行改进. 改进后的模型能够综合考虑用户喜好以及访问代价, 并给出相应的推荐结果.
在原本的LSTM损失函数中, 兴趣点的预测向量与真实表征向量之间的均方误差(Mean Squared Error, MSE)被用来衡量模型的准确度, 其推荐结果更偏向于用户的喜好. 为了使模型在关注用户喜好的同时能够兼顾兴趣点序列中的距离要素进行推荐, 本文提出了基于距离优化的LSTM模型(LSTM based on Distance Optimization, DO-LSTM), 对原本的损失函数做出了如下改进:
| $\begin{split} {\cal L} = &\frac{1}{{|H|}}\sum\nolimits_{{H_i} \in H} \\ &{\frac{1}{{\left( {||{H_i}| - ts - 1|} \right)}}} \left( {\sum\nolimits_{t = ts + 1}^{|{H_i}|} {MSE\left( {\widehat {{q_t}},{q_t}} \right)} + \tau D\left( {{L_i}} \right)} \right) \end{split} $ | (6) |
| $D\left( {{L_i}} \right) = \sum\nolimits_{t = ts}^{|{H_i}|} {dist\left( {pos\left( {\widehat {{q_t}}} \right),pos\left( {\widehat {{q_{t - 1}}}} \right)} \right)} $ | (7) |
该算式中, H表示n个用户序列的集合, 即
在训练的过程中, 使用自适应梯度算法(AdaGrad)[12]方法对该损失函数进行最小化. AdaGrad以每次迭代的历史梯度平方和为分母调整模型中不同参数的学习率, 能够更有效地使模型收敛.
最终, 如图2所示, LBSN中的用户-兴趣点交互信息首先以社交网数据为辅助信息形成混合矩阵; 基于该混合矩阵, 用户和兴趣点的隐特征向量被提取; 最后, 根据用户的兴趣点访问序列以及所提取的兴趣点特征向量, 以序列中所隐含的时空上下文关系为用户推荐一组符合用户偏好以及距离要求的兴趣点.
4 实验本文使用Gowalla和Yelp的数据进行研究与实验. Gowalla数据集中包含了32510个地点与18737个用户的兴趣点访问轨迹, 共计1278274条签到数据. Yelp数据集中包含了30887个地点与18995个用户的兴趣点访问轨迹, 共计860888条签到数据. 此外, 在两个数据集中均包含用户关系网数据.
4.1 实验设置对于这两种数据集, 本文按时间顺序取前80%的数据为训练集, 后20%的数据为测试集. 在基于LSTM与距离优化的序列推荐模型中, 兴趣点本身的推荐准确率要比兴趣点的排序正确程度更加重要, 且兴趣点的排序并非单纯依赖于用户的偏好, 而是综合考虑了访问兴趣点所产生的距离损失. 因此, 以Precision@ N衡量模型的推荐性能, 即在未来的长度为N的序列中, 用户接下来确实要访问的兴趣点所占的比例.
本文选取了以下几种算法模型进行实验对比:
1) 基于协同过滤(CF)的推荐算法: 在近百万条签到数据中, 对每一个用户寻找访问过相同兴趣点的用户, 并标记为此用户的近邻用户. 根据近邻程度, 即目标用户与近邻用户的兴趣点偏好相同程度, 为目标用户推荐近邻用户所偏好的兴趣点. 此类方法同样不关心用户或兴趣点本身的特征, 近邻用户的计算基于用户与兴趣点的交互行为.
2) 基于奇异值分解(SVD)的算法: SVD类模型试图将用户-兴趣点之间的交互数据转化为以用户id为行、以兴趣点id为列、以用户对兴趣点访问频次为元素值的矩阵, 以矩阵元素实际值与分解项相乘所得的预测值之间的误差为损失函数进行训练. 通过SVD模型, 矩阵被分解为两个更小规模的矩阵, 矩阵的行或列代表每一个用户或兴趣点的隐特征向量. SVD的目的在于对未访问部分进行访问频次预估, 从而全面挖掘用户偏好的兴趣点, 并按照频次大小排序推荐给用户. 本实验中, 使用biasedSVD[10]模型进行测试.
3) 基于自注意力机制(self-attention)的算法: 多用于NLP领域中语义分析相关的任务中, 其目的是根据整个句子中词语之间的联系, 判断出相对值得注意, 即能够完整表述句子意义的部分. 而AttRec[13]模型则是将用户的兴趣点访问序列看作NLP中的“句子”, 并通过自注意力机制判断序列中用户最为关注的兴趣点, 该兴趣点往往能够全局性地代表用户访问序列所隐含的整体偏好.
4) 基于长短期记忆网络(LSTM)与距离优化的算法: 即本文所提出的DO-LSTM模型. 该模型参考了LSTM在语义分析任务中的用途, 根据兴趣点之间的时空上下文推断用户在未来的n个时刻可能访问的兴趣点. 和其它的基于序列的推荐算法不同, 本模型对未来序列的预测并不完全依赖于用户的喜好, 兴趣点的可达性(即访问代价)也是该模型的关注点之一.
4.2 实验效果取
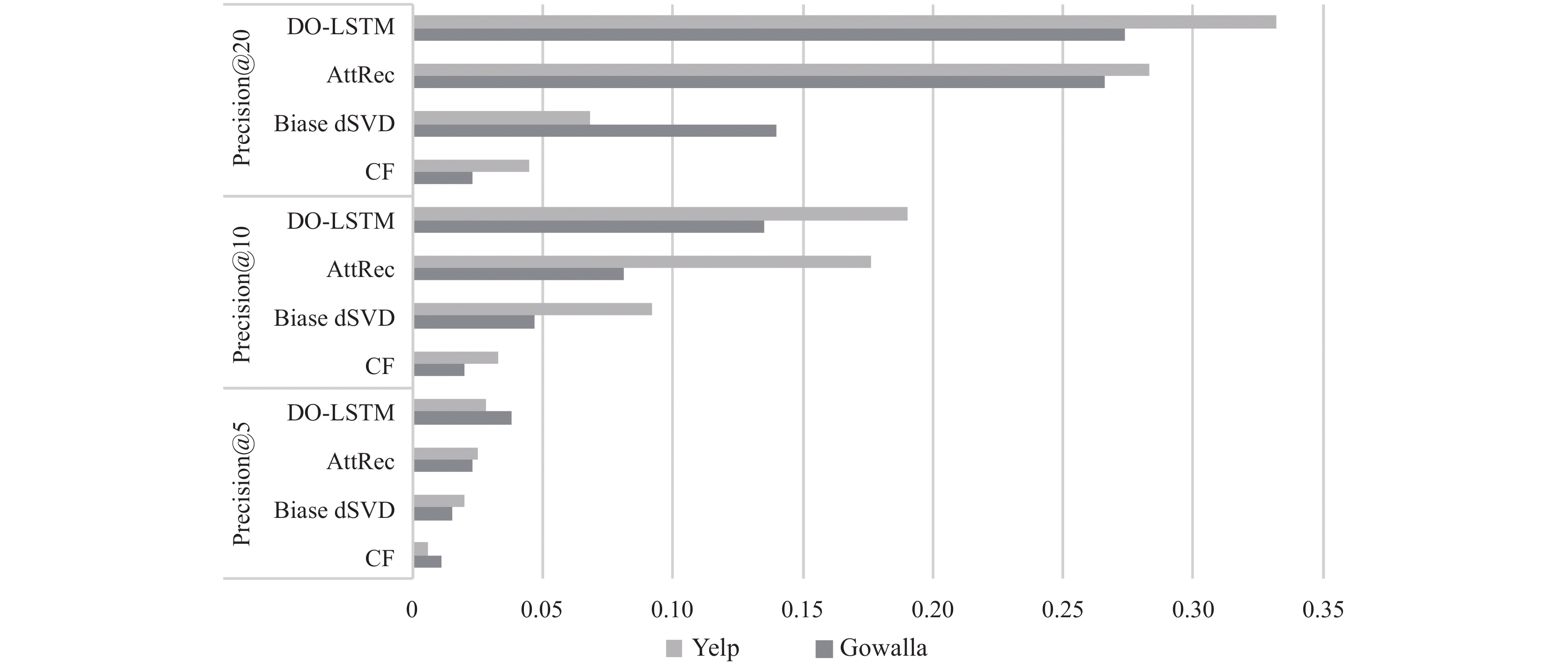
|
图 3 Gowalla和Yelp数据集中的准确率对比柱状图 |
由图3可以看出, 在完整性有限的数据集中, DO-LSTM模型所表现出的准确率与召回率比其它的算法模型较好.
5 结论与展望本文对兴趣点推荐研究相关的现状进行分析, 针对兴趣点偏好推荐以及兴趣点可达性提出DO-LSTM模型. 相比于其它的兴趣点推荐模型, 该模型能够在兴趣点交互信息较为促狭的情况下为用户生成一系列偏好的兴趣点, 且这些兴趣点对当前用户具有较好的可达性. 然而, 在兴趣点推荐领域中, 本模型仍然具有需要改进的地方:
首先, 该模型能够仅根据LBSN中用户-兴趣点的访问序列、兴趣点地理位置以及简单的用户社交关系网为用户生成相对准确且完整的偏好兴趣点. 然而该模型在丰富的LBSN数据中的性能表现可能不如其它模型, 如基于地理-社会-评论关系的推荐方法[14]以及融合地理信息的推荐方法[15], 这两种模型分别将评论关系以及兴趣点详细信息作为参考因素优化推荐性能. 因此在后续的改进工作中, 将继续收集兴趣点的详细信息以及用户-兴趣点评论关系, 对模型进行重新设计.
其次, 由于用户社交关系网信息过于简单, 仅包含成对的用户id信息, 该模型对该信息的利用并不充分, 仅以用户之间的社交关系距离为考量预估用户对兴趣点的偏好程度. 而改进的方向主要分为两个方面: 一是丰富社会关系网的边信息, 使关系类型有所区分(如朋友关系、父母关系等). 二是使用图神经网络(Graph Neural Networks, GNN)[16]等更加精确的模型分析社交网中每一个用户与其它用户的相互影响程度, 从而准确地评估出当前用户在其它近邻用户的影响下对兴趣点的偏好.
综上, 在未来的工作中, 本模型将根据以上不足之处进行改进, 使其能够用于更加复杂的业务环境中.
| [1] |
Ye M, Yin PF, Lee WC, et al. Exploiting geographical influence for collaborative point-of-interest recommendation. Proceedings of the 34th International ACM Sigir Conference on Research and Development in Information Retrieval. Beijing, China. 2011. 325–334.
|
| [2] |
Koren Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas, NV, USA. 2008. 426–434.
|
| [3] |
Ma H, Yang HX, Lyu MR, et al. SoRec: Social recommendation using probabilistic matrix factorization. Proceedings of the 17th ACM Conference on Information and Knowledge Management. Napa Valley, CA, USA. 2008. 931–940.
|
| [4] |
Guo GB, Zhang J, Yorke-Smith N. TrustSVD: Collaborative filtering with both the explicit and implicit influence of user trust and of item ratings. Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. Austin, TX, USA. 2015. 123–129.
|
| [5] |
龚卫华, 沈松. 基于社区发现的兴趣点推荐. 计算机科学, 2019, 46(12): 63-68. DOI:10.11896/jsjkx.190400440 |
| [6] |
Koren Y. Collaborative filtering with temporal dynamics. Communications of the ACM, 2010, 53(4): 89-97. DOI:10.1145/1721654.1721677 |
| [7] |
Hidasi B, Quadrana M, Karatzoglou A, et al. Parallel recurrent neural network architectures for feature-rich session-based recommendations. Proceedings of the 10th ACM Conference on Recommender Systems. Boston, MA, USA. 2016. 241–248.
|
| [8] |
Tang JX, Wang K. Personalized top-N sequential recommendation via convolutional sequence embedding. arXiv: 1809.07426, 2018.
|
| [9] |
蒋宗礼, 王逸鹤. 基于序列挖掘的兴趣点推荐算法. 北京工业大学学报, 2019, 45(9): 853-858. |
| [10] |
Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer, 2009, 42(8): 30-37. DOI:10.1109/MC.2009.263 |
| [11] |
Li Z, Zhao HK, Liu Q, et al. Learning from history and present: Next-item recommendation via discriminatively exploiting user behaviors. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London, UK. 2018. 1734–1743.
|
| [12] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. The Journal of Machine Learning Research, 2011, 12: 2121-2159. |
| [13] |
Zhang S, Tay Y, Yao LN, et al. Next item recommendation with self-attention. arXiv: 1808.06414, 2018.
|
| [14] |
孟祥福, 毛月, 张霄雁, 等. 基于地理-社会-评论关系的典型化兴趣点推荐方法. 小型微型计算机系统, 2019, 40(11): 2431-2438. DOI:10.3969/j.issn.1000-1220.2019.11.033 |
| [15] |
杜亚洲, 张书钦, 王金洋, 等. 融合地理信息的兴趣点推荐. 计算机科学与应用, 2020, 10(4): 629-640. |
| [16] |
Zhou J, Cui GQ, Zhang ZY, et al. Graph neural networks: A review of methods and applications. arXiv: 1812.08434, 2019.
|
 2021, Vol. 30
2021, Vol. 30



