2. 中国科学院大学, 北京 100049;
3. 沈阳中科数控技术股份有限公司, 沈阳 110168
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shenyang CASNC Technology Co. Ltd., Shenyang 110168, China
在这个信息化时代中, 随着计算机技术的高速发展, 信息的产生、收集和存储能力不断增强, 产生了越来越多的数据. 数据类型不断增多: 图像、文本、音频等. 时间序列型数据不仅只在时间上具有前后关系, 任何逻辑上具有先后关系且不可改变的数据都是时间序列型数据. 所以, 时序数据广泛存在于各个数据类型中. 因此, 时间序列型数据得以在医疗诊断、工业生产与控制、运动检测、生物识别、考古研究等生活的各个领域中应用广泛. 但是, 通常采集到的时序型数据在一个维度上会不断增加, 所以时间序列型数据具有数据维度高、数据量大[1]的特点. 若直接使用传统的数据挖掘技术对时间序列数据进行分析不仅需要耗费大量的时间和存储成本[2], 还很可能难以分析, 得不到结果.
为了在保留时间序列有效特征的前提下, 减少数据量, 对数据进行压缩, Keogh、Chu和Hart提出了PLR[3]表示方法. PLR方法是时间序列的分段线性表示方法. 该方法的主要思想是从原始时间序列中提取重要特征点, 用这些特征点连接起来的直线段代表原时间序列. 这种方法用寻找到的关键点更直观地展示了原始时间序列的特征. Ehmke等[4]提出了自顶向下的TD方法寻找关键点. 与文献[4]不同, Theodosios等[5]以自底向上的BU方法寻找关键点. 两个方法都是时间序列分段线性表示的经典算法, 但都存在时间复杂度较高的问题. 为了提高查找效率, Chakrabarti等[6]引入了滑动窗口, 降低了查找的时间复杂度. 林意等[7]从时间序列的形态出发, 将其与几何图形结合, 提出了PLR_WFTP方法. 詹艳艳等[8]则将斜率变化(PLR_SEEP)作为关键点的判断指标. 汤晶晶等[9]通过点边界面积(PLR_AP)作为判断点的重要性, 以此来作为该点是否能成为关键点的依据. 肖辉等[10]提出了基于时态边缘算子的TEO方法.
本文研究了时间序列的状态, 发现了时间序列的波动特性, 在结合前人研究的基础上, 提出了基于时间序列波动性的分段线性表示方法. 该算法将时间序列的趋势分为上、下两层, 在此基础上提取关键点, 将原来3点之间的比较扩大为9个点, 很好地保留了时间序列的全局特征. 同时, 该算法在关键点的提取过程中, 忽略了对趋势变化没有贡献的点. 在提取连续型趋势段中的关键点时得到的点数更少, 结果更精确, 有更小的拟合误差.
2 基本定义定义1. 时间序列. X(t)={x(t1), x(t2), x(t3), …, x(tm)}是一个长度为m的有序数据集合. 其中x(ti)=<xi, ti>, (i=1, 2, 3, …, m; m∈N+)表示X在ti时刻采集到的数据值为xi, xi可以是单个数据值, 也可以是一个数据集合. 通常, t1=0, Δt=1, (Δt=ti−ti−1). 因此, 时间序列X可简单地记为X={x1, x2, xi, …, xm }, (m≥1, m∈N+). 当数据空间的维度为N时, 该时间序列的每个数据项都有n个分量, 则X的第i个数据项可表示为:
| $ x_i=\left\{x_{i1}, x_{i2}, x_{ij}, \cdots, x_{in}\right\},\;\;j=1, 2, \cdots, n, n\in N^+$ | (1) |
其中, xij表示xi在第j个维度的分量坐标值. 本文只考虑数据空间为一维的情况, 即j=n=1. 由于时间序列的广义化, 采集到的数据值xi可以是多种类型的, 如: 符号、文本、图像、声音等. 本文只考虑xi是实值型数据的情况.
定义2. 拟合误差. 设原时间序列X={ x1, x2, x3, …, xn }, 分段操作得到的分段点集合为X′={x1′, x2′, x3′, …, xk′}, 其中x1= x1′, xn=xk′, k<n. 线性插值后得到的新时间序列为XC={xc1, xc2, xc3, …, xcn}. 定义新时间序列与原时间序列之间的欧式距离为拟合误差. 其公式如下:
| $E = \sqrt {\sum\limits_{i = 1}^n {\left( {x_i - x_i^c} \right)} } $ | (2) |
定义3. 压缩率. 原时间序列X={ x1, x2, x3, …, xn }, 经过PLR算法得到的新时间序列X′={x1′, x2′, x3′, …, xk′}. 定义该算法的压缩率如下:
| $\left( {1 - \frac{k}{n}} \right) \times 100{\text{%}} $ | (3) |
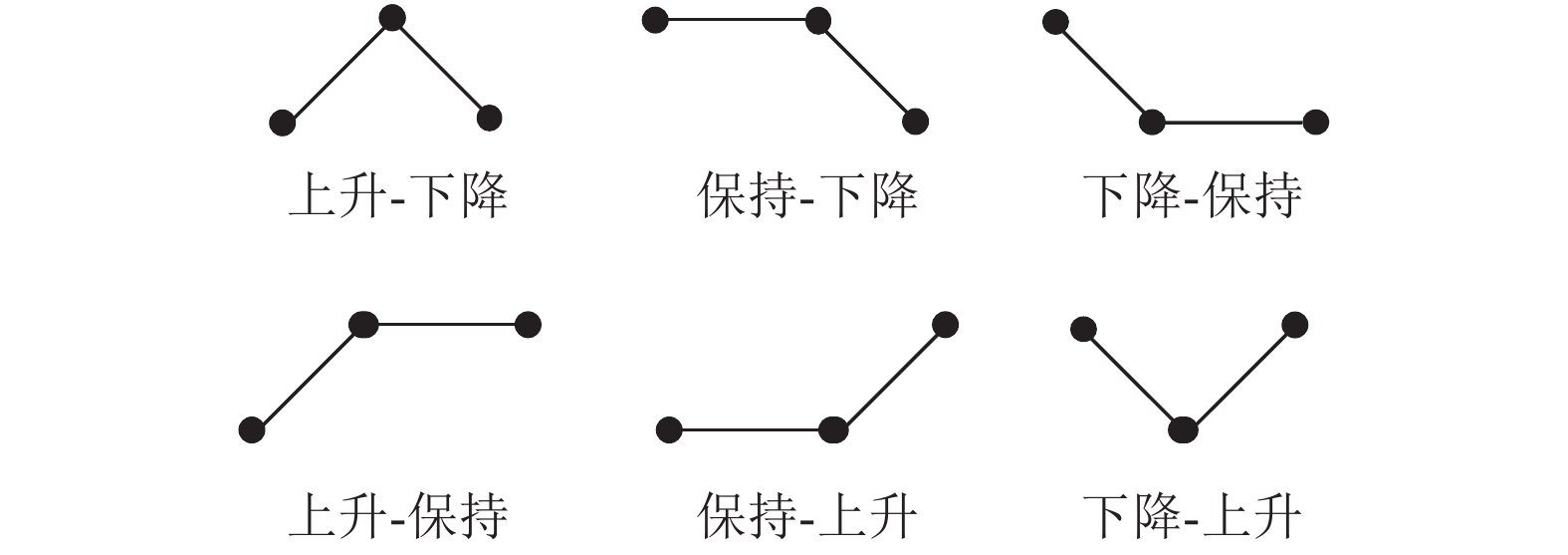
研究中, 观察到时间序列中的点总是波动的, 在整体上呈现出某种趋势和趋势变化. 研究发现, 时间序列的变化可细分为“上升”、“下降”、“保持”这3种基本趋势. 基于这3种基本趋势, 3个相邻的时间序列点可呈现出9种趋势变化[11]. 其中有6种发生趋势转折, 其余3种保持趋势不变. 基本趋势模式如图1所示.

|
图 1 基本趋势模式 |
|
图 2 6种趋势转折 |

|
图 3 4种趋势保持 |
3.2 上、下层备选点
研究发现, 对时间序列3点间趋势变化模式的描述可以扩展到整个时间序列. 由于序列总是波动的, 在某一时间段内才稳定呈现出上升、下降、保持其中一种趋势. 将这些时间段中的趋势连接起来, 就得到了时间序列整体趋势变化模式. 在对时间序列进行分段时, 无论是基于斜率[8]的方法还是引入几何中三角形[9,11-13]的方法, 都关注于极值点和拐点. 从极值点和拐点中提取重要特征点. 因此, 现有的时间序列分段方法很容易陷入局部最优的状态, 从而忽略了时间序列的全局特征. 针对现有分段方法忽略了时间序列整体特征这一问题, 本文研究了时间序列的发展趋势, 发现时间序列的趋势总是由波动点构成的: 时间序列中的点总是波动的, 不是向上波动就是向下波动. 因此可以认为, 波动点描述了时间序列的变化趋势. 基于此发现, 本文提出了时间序列分层的概念, 为关键点的选取打下基础. 其定义如下:
设有时间序列X(t)={x(t1), x(t2), x(t3), …, x(tn)}. 其中x(ti), i=1, 2, 3, …, n表示该序列在时刻ti的数据值为x(ti), 简写为xi.
定义4. (上层备选点). 对于时间序列中的任意一点xi, 若满足xi>xi−1或xi>xi+1, 则称xi属于上层备选点.
定义5. (下层备选点). 对于时间序列中的任意一点xi, 若同时xi<xi−1或xi<xi+1, 则称xi属于下层备选点.
性质. 时间序列的上下两层备选点, 分别保留了时间序列上层和下层的重要特征.
3.3 关键点时间序列分段线性表示方法的主要内容是找到时间序列中的关键点, 即时间序列中左右两边趋势发生变化的点. 由时间序列3点间的趋势变化模式可知, 只有在趋势转折点处的趋势才发生变化. 同时, 若一个点不是趋势转折点, 则它一定是趋势保持点. 所以, 时序中的点除趋势保持点以外都是趋势转折点, 即关键点. 基于此发现, 本文分别遍历上、下层备选点, 判断其与相邻备选点之间的大小, 若满足保持趋势关系, 则剔除掉. 遍历完成之后得到的剩余点就是关键点.
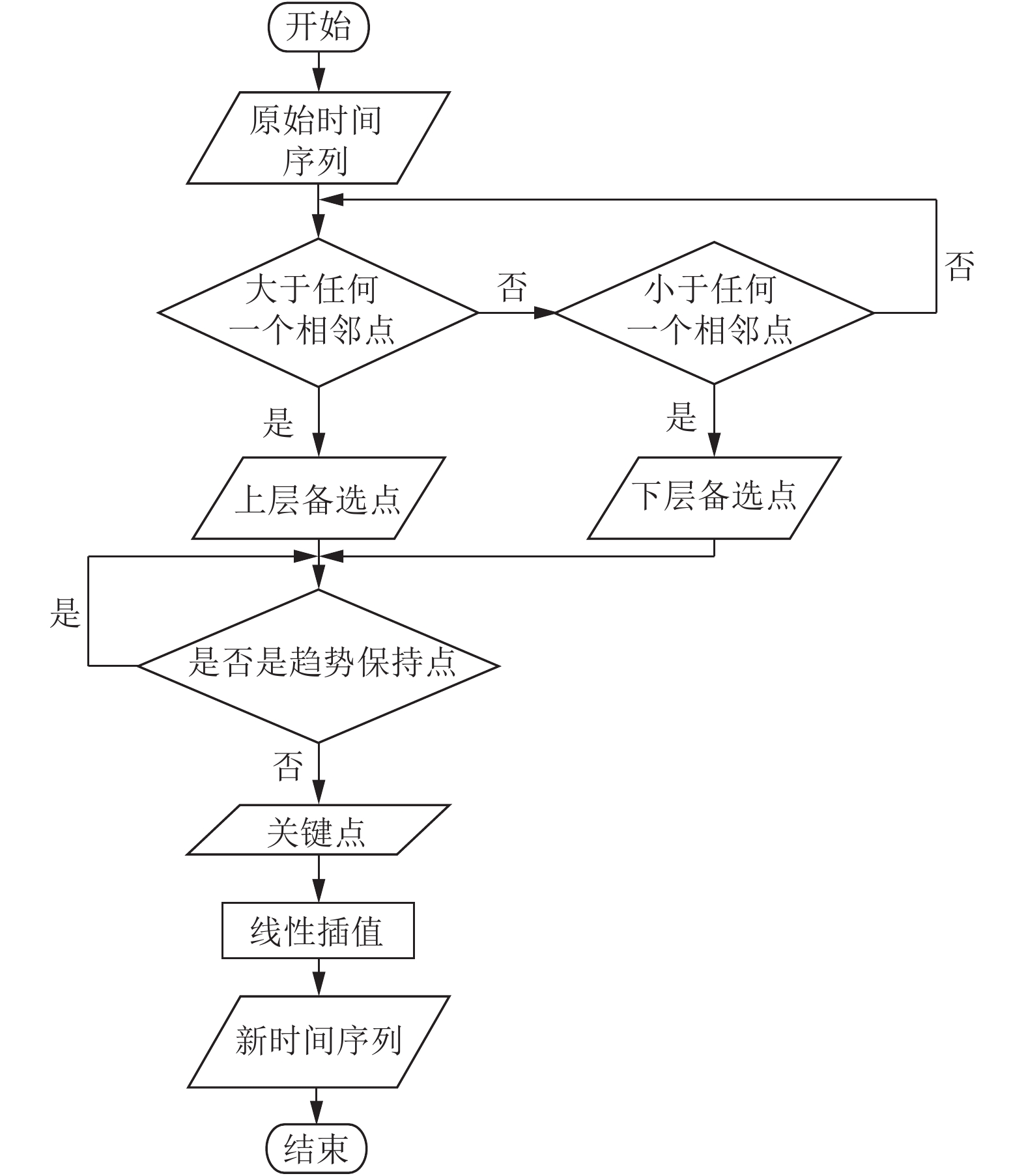
3.4 算法描述算法流程图, 如图4所示.
输入: 时间序列X={x1, x2, x3, …, x1}
步骤1. 提取备选点
比较xi与其相邻点的大小, 若xi>xi−1则认为该点是上层备选点. 将该点的值保存到up_v数组中, 该点的位置信息保存到up_k数组中; 若xi<xi+1或xi<xi−1, 则认为该点是下层备选点. 将该点的值保存到low_v数组中, 该点的位置信息保存到low_k数组中.
步骤2. 提取关键点
遍历up_v和up_k数组, 若当前点up_v[i]不满足up_v[i+1]>up_v[i]> up_v[i−1], 同时不满足up_v[i+1]<up_v[i]<up_v[i−1], 即当前上层备选点不是趋势保持点, 那么当前点是关键点. 将该点的数值信息及位置信息保存到up集合中, 以该点的位置信息作为集合的key值, 该点的数值信息作为集合的value值; 遍历low_v和low_k数组, 若当前点low_v[i]不满足low_v[i+1]>low_v[i]> low_v[i−1], 同时不满足low_v[i+1]<low_v[i]<low_v[i−1], 即当前下层备选点不是趋势保持点, 则当前点是关键点. 将该点的数值信息及位置信息保存到low集合中. 同样, 以该点的位置信息作为low集合的key值, 该点的数值信息作为low集合的value值.
注意到, 无论是上层备选点还是下层备选点都不包括连续相邻三点值相等的情况. 这是因为, 在波动点的提取过程中, 忽略了不发生波动的点. 然而, 这对关键点的提取并没有影响. 因为, 关键点只在极值点和拐点中包括.
步骤3. 将up集合和low集合合并, 并按照key值排序. 将排好序的数据放入关键集合.
步骤4. 采用线性插值方法对关键点区间进行拟合.
输出: 新的序列.
|
图 4 算法流程 |
从以上的算法描述可以看出, 该算法主要分成两个部分: 第1部分扫描时间序列, 提取备选点; 第2部分从备选点序列中提取关键点. 经过优化, PLRGFKP算法只需对时间序列进行一次扫描, 其时间复杂度为O(n).
4 实验分析 4.1 实验数据本文首先对工业时序数据进行分段线性表示, 以PCoE数据集中的铣削数据集为例, 该数据集由UC Berkeley的the BEST lab[14]实验室提供, 记录了铣削刀片VB的磨损程度.
为了验证本文算法的适用性. 本文选取了来自不同领域的UCR公开数据集[15]中的6条实际时间序列作为实验数据, 并用来比较各算法的性能. 其数据信息如表1所示.
| 表 1 实验数据集 |
数据表中显示了6条时间序列的名称和长度. 该数据集中包括了长度较短、长度一般、长度较长的3种时间序列. HandOutLines (HOL)序列长度最长. 其中, RefrigerationDevices (RD)序列呈周期性变化、UWaveGestureLibraryAll (UWLA)序列变化没有规律、Phoneme序列斜率变化集中.
4.2 实验方法本文实验环境为: Windows10操作系统、Inter-i5处理器、8 GB内存. 开发环境为Python3.8.
在对实验数据进行实验之前, 为了保证一致性, 本文对数据进行了归一化处理, 即对所有数据进行以下操作:
| $x_i = \frac{{x_i - min }}{{max - min }}$ | (4) |
其中, min是该时序数据中的最小值, max是该时序数据中的最大值. 该操作将时序数据中所有的值都变换到了[0, 1]内.
另外, 本文共选取了4种时间序列分段线性表示算法与本文算法做比较. 以原始时间序列作为输入, 新的时间序列作为输出. 分别比较了通过各算法得到的新序列与原始时间序列之间的拟合误差. 本文采用的拟合方式为线性插值法: 在每个区间的两个端点间插入有限个点, 依次连接相邻两个点得到区间的直线段, 从而将区间连接起来得到一整条新序列.
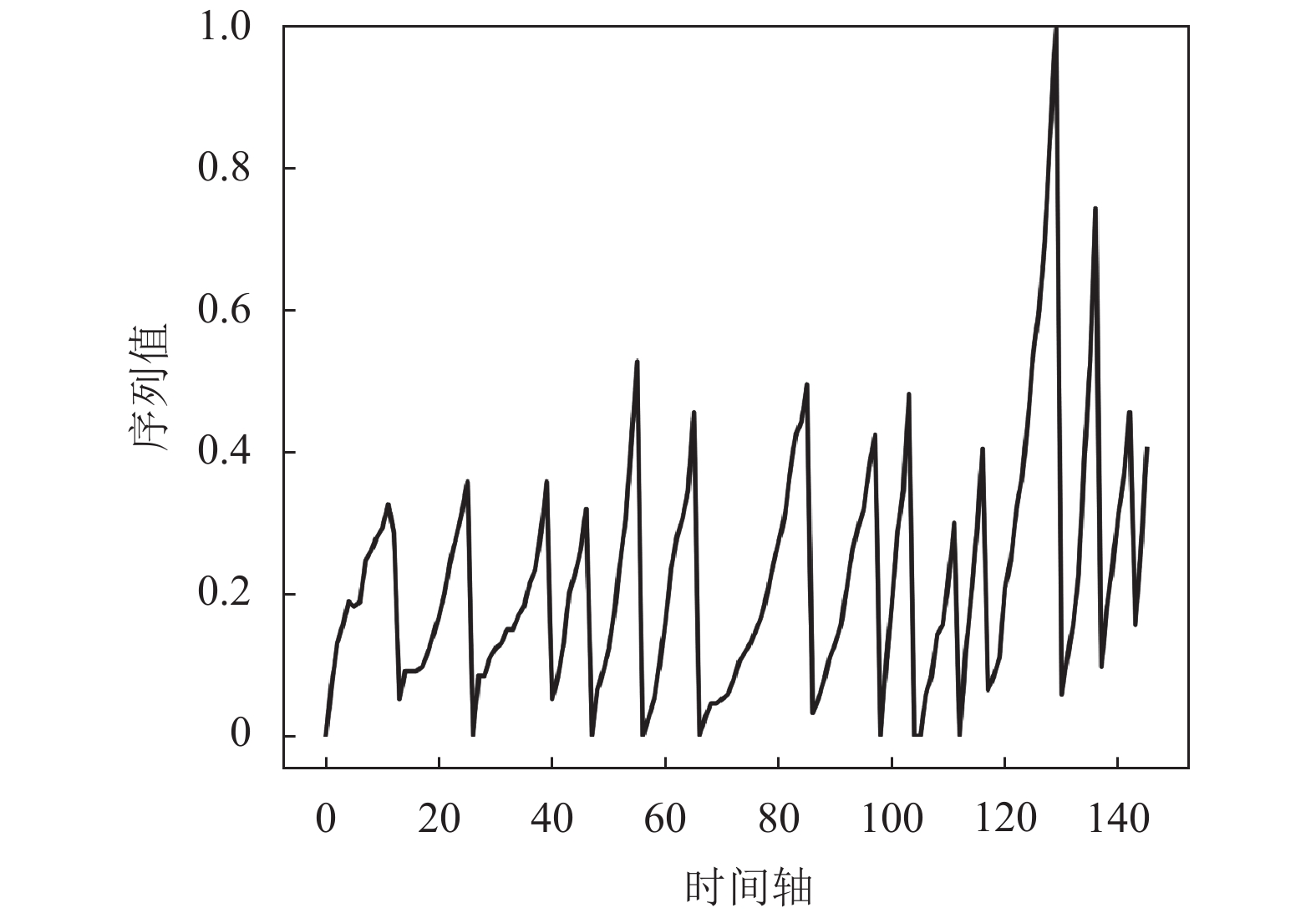
4.3 实验结果及分析如图5所示, 是铣削过程中VB切片磨损程度的原始时间序列. 该数据集中有数据缺失的现象, 因为缺失数据对序列没有直接影响, 所以, 实验过程中对缺失值进行了丢弃处理. 图6是经过分段线性表示后的新序列. 由图可知, 新的序列减少了原始序列中的波动, 很好地保留了其主要发展趋势.
|
图 5 VB磨损原始序列(分段表示前) |

|
图 6 VB磨损PLR序列(分段表示后) |
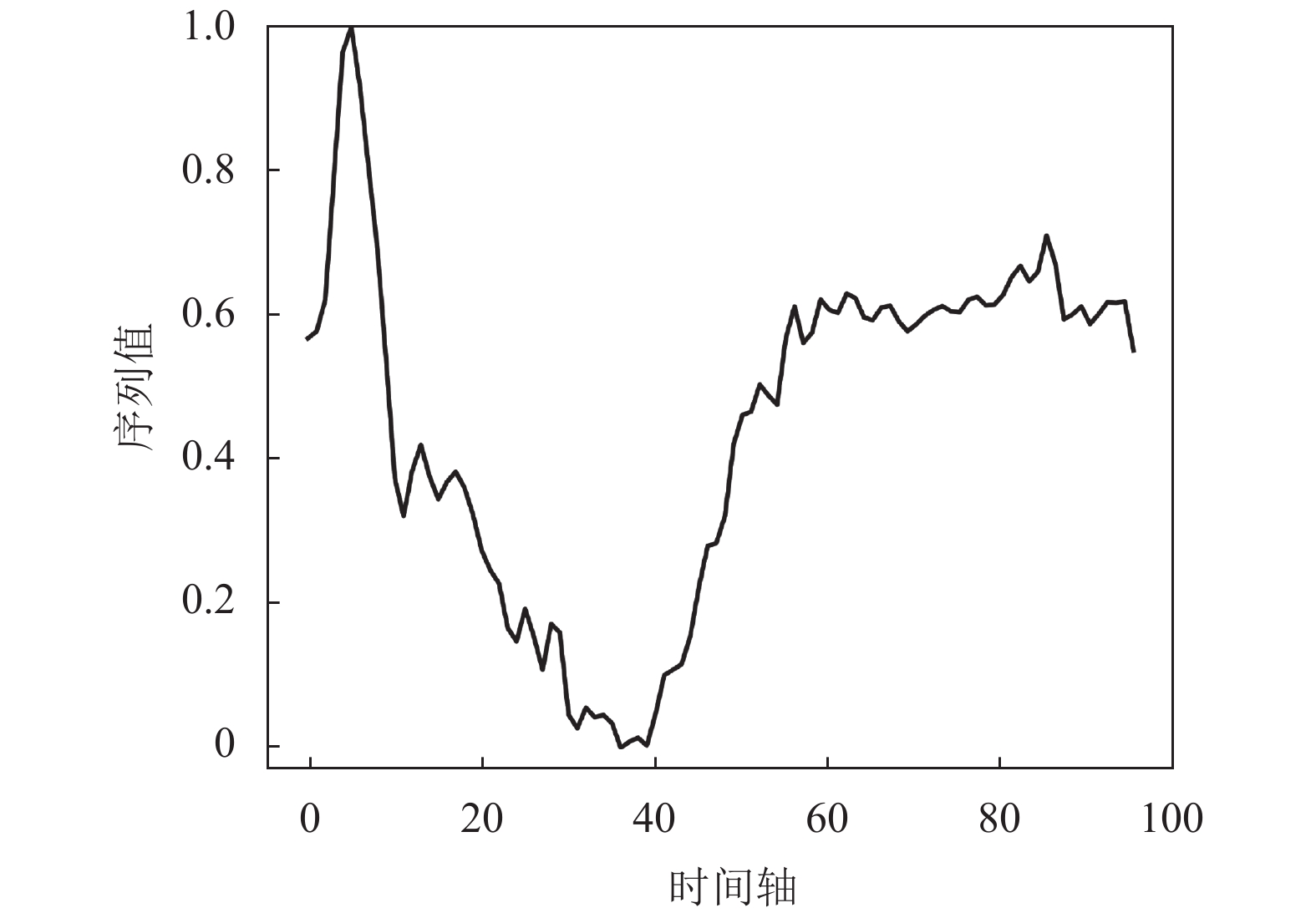
以UCR数据集中的ECG信号数据为例, 图7和图8分别是ECG信号分段线性表示前的序列和ECG信号分段表示后的序列. 对比两图可知, 该线性分段方法在减少波动的情况下, 很好地保留了原始时间序列的发展趋势.
4.4 算法对比拟合误差是评价时间序列分段线性表示算法的一项重要指标[16-19], 其计算方式如式(2)所示. 一般来说, 拟合误差越小, 得到的新序列对原始时间序列的拟合程度越高, 算法的性能越好. 表2展示了在压缩率为80%的情况下, 各算法在实验数据上的拟合误差.
|
图 7 ECG原始序列(分段表示前) |
|
图 8 ECG的PLR序列(分段表示后) |
| 表 2 80%压缩率下各算法拟合误差 |
表2中加粗的数据表示最小拟合误差. 从表中可以看出, 在6条时间序列中, 本文提出的GFKP在其中4条时间序列上拟合误差最小, 在另外2条时间序列上的拟合误差与最小拟合误差相差不大. 因此, 实验表明本算法具有良好的适应性.
压缩率是评价算法的另一项重要指标[20-24], 其计算方式如式(3)所示. 压缩率越高, 对数据的压缩程度越高, 得到的分段数目就越小. 一般来说, 同一个算法的压缩率越高, 拟合误差也会随之增加. 图9展示了4种PLR算法与本文算法对UWLA序列在不同压缩率下的拟合误差对比.

|
图 9 各算法在不同压缩率下的拟合误差 |
由图9可知, 随着压缩率的增加, 拟合误差逐渐增大, 但是, GFKP算法的拟合误差始终较低. 因此, GFKP算法对原始序列的拟合度较好.
5 总结与展望时间序列的线性分段表示方法的主要内容是提取时间序列中的关键点. 通常认为关键点来自于极值点和拐点, 因此大多数学者只关注于时间序列的局部特征, 这不仅容易陷入局部最优的状态, 还忽略了时间序列整体的发展趋势[25-28]. 针对这一问题, 本文提出了基于时间序列波动性的分段线性表示方法. 该算法首先提取出时间序列的波动点, 保留时间序列的发展趋势. 在此基础上, 找到关键点. 依次将找到的若干个关键点用线性插值的方法进行拟合, 拟合的结果就是时间序列的GFKP表示. GFKP表示算法计算简单、容易实现、时间复杂度O(n). 该算法不仅能够在工业时序数据上取得良好的分段效果, 与其他分段线性表示算法相比, 能够更好地体现出时间序列的发展趋势和全局特征, 且有较小的拟合误差和较好的适应性. 接下来将研究时间序列的特征转换. 时间序列的重要特征信息主要存在于其关键点中. 时间序列的特征转换是指在提取到关键点后, 转化这些特征, 使其可以结合主流的数据挖掘算法进行研究, 这是一个有价值的研究方向.
| [1] |
朱志静. 基于趋势和特征子序列的时间序列数据挖掘研究[硕士学位论文]. 无锡: 江南大学, 2019.
|
| [2] |
刘意杨, 李俊朋, 白洪飞, 等. 基于转折点和趋势段的时间序列趋势特征提取. 计算机应用, 2020, 40(S1): 92-97. |
| [3] |
Keogh E, Chu S, Hart D, et al. An online algorithm for segmenting time series. Proceedings of 2001 IEEE International Conference on Data Mining. San Jose, CA, USA. 2001. 289–296.
|
| [4] |
Ehmke JF, Meisel S, Mattfeld DC. Floating car based travel times for city logistics. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 338-352. DOI:10.1016/j.trc.2011.11.004 |
| [5] |
Pavlidis T, Horowitz SL. Segmentation of plane curves. IEEE Transactions on Computer, 1974, C-23(8): 860-870. |
| [6] |
Keogh E, Chakrabarti K, Pazzani M, et al. Dimensionality reduction for fast similarity search in large time series databases. Knowledge and Information Systems, 2001, 3(3): 263-286. DOI:10.1007/PL00011669 |
| [7] |
林意, 朱志静. 基于趋势的时间序列分段线性化算法. 重庆大学学报, 2019, 42(3): 92-98. |
| [8] |
詹艳艳, 徐荣聪, 陈晓云. 基于斜率提取边缘点的时间序列分段线性表示方法. 计算机科学, 2006, 33(11): 139-142, 161. DOI:10.3969/j.issn.1002-137X.2006.11.038 |
| [9] |
汤晶晶, 李晋宏. 基于趋势转折点边界面积的时间序列分段算法. 软件, 2019, 40(12): 195-200. DOI:10.3969/j.issn.1003-6970.2019.12.043 |
| [10] |
肖辉, 马海兵, 龚薇. 基于时态边缘算子的时间序列分段线性表示. 计算机工程与应用, 2008, 44(19): 156-159. DOI:10.3778/j.issn.1002-8331.2008.19.047 |
| [11] |
廖俊, 于雷, 罗寰, 等. 基于趋势转折点的时间序列分段线性表示. 计算机工程与应用, 2010, 46(30): 50-53, 81. |
| [12] |
尚福华, 孙达辰. 基于时间序列趋势转折点的分段线性表示. 计算机应用研究, 2010, 27(6): 2075-2077, 2092. DOI:10.3969/j.issn.1001-3695.2010.06.022 |
| [13] |
戴爱明, 高学东. 时间序列三角极值点线性分段算法. 南昌航空大学学报(自然科学版), 2009, 23(2): 25-28, 41. |
| [14] |
National Aeronautics and Space Administration. https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/. [2020-07-15].
|
| [15] |
Chen YP, Keogh E, Hu B, et al. The UCR time series classification archive. www.cs.ucr.edu/~eamonn/time_series_data/. [2020-07-15].
|
| [16] |
李爱国, 覃征. 大规模时间序列数据库降维及相似搜索. 计算机学报, 2005, 28(9): 1467-1475. DOI:10.3321/j.issn:0254-4164.2005.09.007 |
| [17] |
Keogh EJ, Pazzani MJ. A simple dimensionality reduction technique for fast similarity search in large time series databases. Proceedings of the 4th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Kyoto, Japan. 2000. 122–133.
|
| [18] |
Zhilyakov EG. Constructing trends of time series segments. Automation and Remote Control, 2017, 78(3): 450-462. DOI:10.1134/S0005117917030067 |
| [19] |
Jaeger H. Observable operator models for discrete stochastic time series. Neural Computation, 2000, 12(6): 1371-1398. DOI:10.1162/089976600300015411 |
| [20] |
Prat KB, Fink E. Search for patterns in compressed time series. International Journal of Image and Graphics, 2002, 2(1): 89-106. DOI:10.1142/S0219467802000482 |
| [21] |
Park S, Lee D, Chu WW. Fast retrieval of similar subsequences in long sequence databases. Proceedings of 1999 Workshop on Knowledge and Data Engineering Exchange. Chicago, IL, USA. 1999. 60–67.
|
| [22] |
Zhou F, De La Torre F, Hodgins JK. Hierarchical aligned cluster analysis for temporal clustering of human motion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(3): 582-596. DOI:10.1109/TPAMI.2012.137 |
| [23] |
Wang L, Li K, Ma Q, et al. Hybrid dynamic learning mechanism for multivariate time series segmentation. Statistical Analysis and Data Mining, 2020, 13(2): 165-177. DOI:10.1002/sam.11448 |
| [24] |
Zhou MN, Yi JZ, Yang JQ, et al. Characteristic representation of stock time series based on trend feature points. IEEE Access, 2020, 8: 97016-97031. DOI:10.1109/ACCESS.2020.2995958 |
| [25] |
Moreno-Garcia J, Moreno-Garcia A, Jimenez-Linares L, et al. Describing time series using fuzzy piecewise linear segments. Kóczy L, Medina-Moreno J, Ramírez-Poussa E, et al. Computational Intelligence and Mathematics for Tackling Complex Problems. Cham: Springer, 2020. 149–155,
|
| [26] |
闫汶和, 李桂玲. 基于shapelet的时间序列分类研究. 计算机科学, 2019, 46(1): 29-35. DOI:10.11896/j.issn.1002-137X.2019.01.005 |
| [27] |
胡宇鹏. 时间序列数据挖掘中的特征表示与分类方法的研究[博士学位论文]. 济南: 山东大学, 2018.
|
| [28] |
解初, 王建东, 韩邦磊, 等. 基于趋势特征聚类的多元相似时间序列的提取. 科学技术与工程, 2020, 20(7): 2786-2793. DOI:10.3969/j.issn.1671-1815.2020.07.038 |
 2021, Vol. 30
2021, Vol. 30



