2. 绍兴市交通建设有限公司, 绍兴 312000
2. Shaoxing City Transportation Construction Co. Ltd., Shaoxing 312000, China
目前我国高速公路总里程已达14.3万公里, 位列世界第一, 高速公路出行承担了主要的交通出行量. 但随着汽车保有量的增多, 长时间大规模的拥堵频发, 不仅降低了通行效率, 还严重影响了民众的出行体验. 为了保障高速公路的通畅, 准确预测交通流量, 提前做好交通信息服务显得十分重要.
早期交通流预测研究主要采用传统统计模型, 如自回归模型[1]、整合移动平均自回归模型[2]、卡尔曼滤波模型[3]、非因素回归模型[4]、小波分析[5]、混沌理论[6]等. 传统的统计模型大多对数据有一定的要求或者假设, 要求模型本身有比较明确的数学形式, 但是在大多数情况下, 人们无法对真实世界数据的分布做任何假设.
而机器学习方法不需要对数据有任何假定, 就可以对复杂多样的数据进行深层次的分析. 如何通过机器学习对复杂多样的数据进行深层次的分析, 高效利用信息已成为当前大数据环境下机器学习的主要研究方向. 杨凡等通过遗传算法对模糊神经网络进行优化, 提出一种混合智能数据挖掘的交通流量预测模型[7]. Li等结合ARIMA模型和SVR, 提出了一种同时捕获线性和非线性的混合策略用于交通流预测, 提高预测精度[8]. Du等提出了一个结合RNNs和CNNs的混合深度学习框架短期交通流预测模型[9]. 这些主要采用机器学习的方法, 对大量历史车流量数据进行分析并构建的预测模型, 虽然取得了一定的准确度, 但是忽略了影响交通流的其他相关因素.
考虑到影响交通流的多种因素, 学者们开始综合这些影响因素对高速公路交通流进行预测. 沈凌等通过ARIMA模型对高速公路收费数据中客货运量相关数据进行机器学习训练, 提出了基于收费数据的高速公路短时客货运输量短时预测研究[10]. 周桐等分别选用改进的时间序列算法和二次指数平滑法对不同类型的车流量进行预测; 通过对各车型的流量预测值进行加权求和, 得到总车流量预测值, 提高了预测精度[11]. Zhang等首次在考虑天气影响的情况下, 针对天气影响将递归神经网络与门控递归单元相结合, 对城市交通流进行预测, 降低了预测错误率[12]. 蔡延光等针对暴雨天气交通流预测问题, 提出一种基于改进布谷鸟算法优化径向基函数神经网络暴雨天气下高速公路交通流预测方法[13].
虽然以上方法都获得了较好的结果, 但多是在单一影响因素或特定情况下进行的实验, 本文提出了一种具有一定普适性的基于多元因素的Bi-LSTM高速公路交通流预测模型. 模型既考虑了影响交通流的多种因素, 又结合Bi-LSTM的模型的结构特性, 考虑到了前后车辆变化对交通流量的影响. 通过对比GRU和LSTM, 表明基于多元因素的Bi-LSTM高速公路交通流预测模型具有较好的预测效果.
2 Bi-LSTM双向长短期记忆网络Bi-LSTM (Bidirectional Long Short Term Memory Networks)是由两个LSTM上下叠加组成[14]. 保留了LSTM保存较长依赖关系的能力, 有利于处理时间间隔较长的事件; 又通过前后向LSTM序列组合的结构, 考虑了前后数据变化的影响.
单个LSTM单元主要通过遗忘门, 更新门和输出门控制数据的流入流出, 实现信息的保护和控制[15]. 其内部结构如图1所示. 遗忘门决定将从细胞状态中丢弃的信息
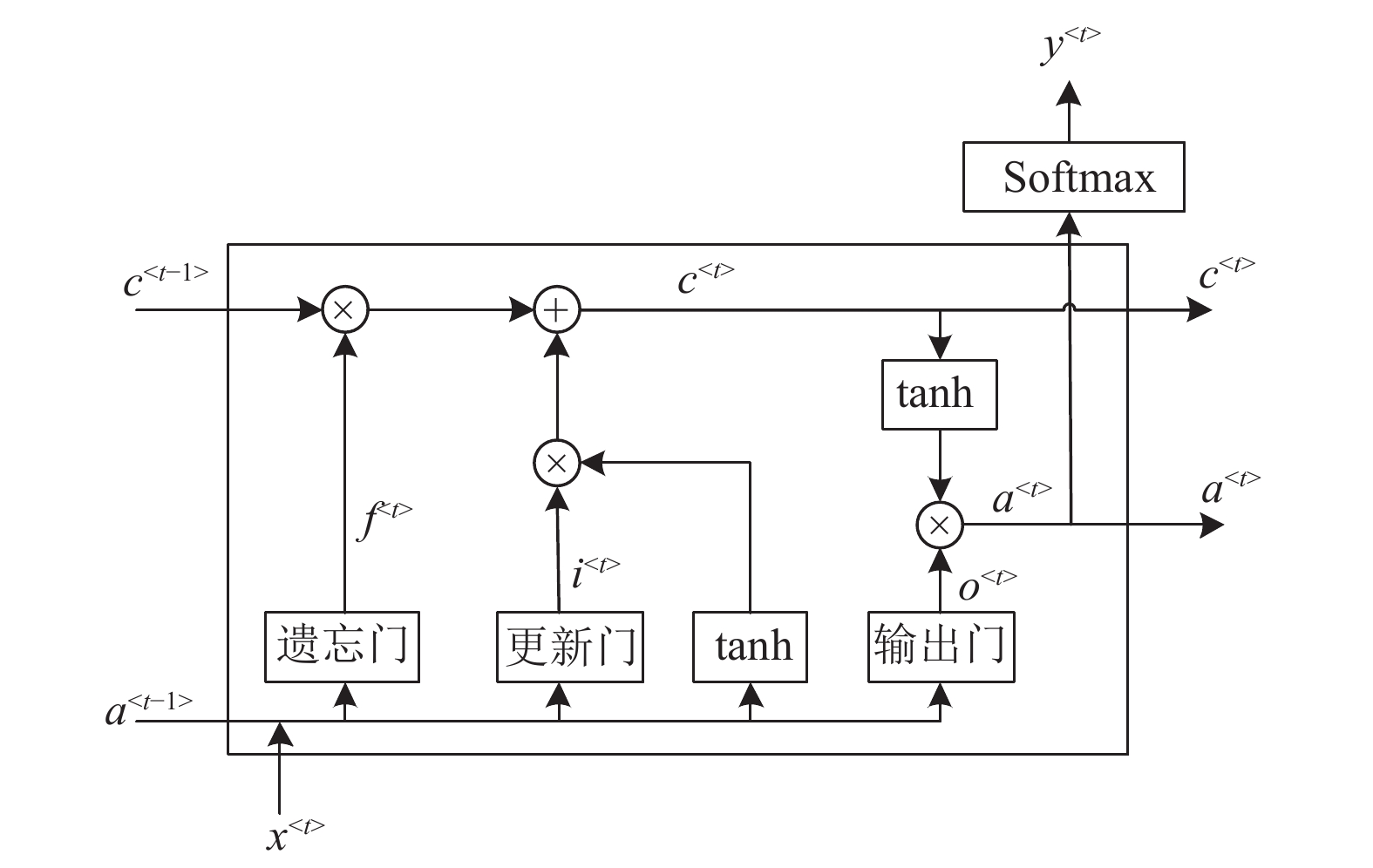
|
图 1 LSTM隐藏层单元的可视化呈现 |
图2是Bi-LSTM模型展开图, 水平方向分别是前向计算的LSTM序列和后向计算的LSTM序列, 以此调整之前的状态以及之后的状态对当前细胞单元状态的影响, 体现了时间序列的双向流动. 竖直方向展示了从输入层、隐藏层到输出层的单向流动.

|
图 2 Bi-LSTM模型展开图 |
目前Bi-LSTM已经成功应用于词性标记[16], 机器阅读理解[17], 词位标注[18]等自然语言处理方向. 将Bi-LSTM应用到交通流预测, 可以利用Bi-LSTM的双向结构, 同时考虑前后车辆变化对交通流量的影响.
3 交通流预测模型建立基于多元因素的Bi-LSTM高速公路交通流预测模型, 整体框架如图3所示, 分为数据预处理模块、模型训练模块和模型评估与预测3个模块.
3.1 数据预处理模块 3.1.1 数据清洗数据清洗是数据预处理的关键步骤, 是对数据进行重新审查和校验. 目的在于删除重复信息、纠正存在的错误, 并提供数据一致性. 本文数据源为高速公路收费收据, 由于收费系统严格控制重复收费问题, 故本数据源无重复数据, 本文数据清洗主要针对不完整数据以及异常数据.
1)异常数据. 如平均时速低于规定最低时速20%以上或高于规定最高时速20%以上的数据; 通行时间远大于最大通行时间或远小于最小通行时间的数据, 进行剔除. 其中
| $v = \frac{{{t_{\rm out}} - {t_{\rm in}}}}{{{{{s}} _{\rm in - out}}}}$ | (1) |
2)不完整数据. 如入口站或出口站信息缺失的、入口时间和出口时间同时不确定的数据, 选择剔除; 仅出口时间缺失的数据, 根据同一出入口的平均通行时间进行修补;
数据清洗后, 所删数据只占原始数据集2%以下, 且修补后的数据满足实验数据质量要求, 在保证了数据信息完整性的前提下进一步提高了数据质量.
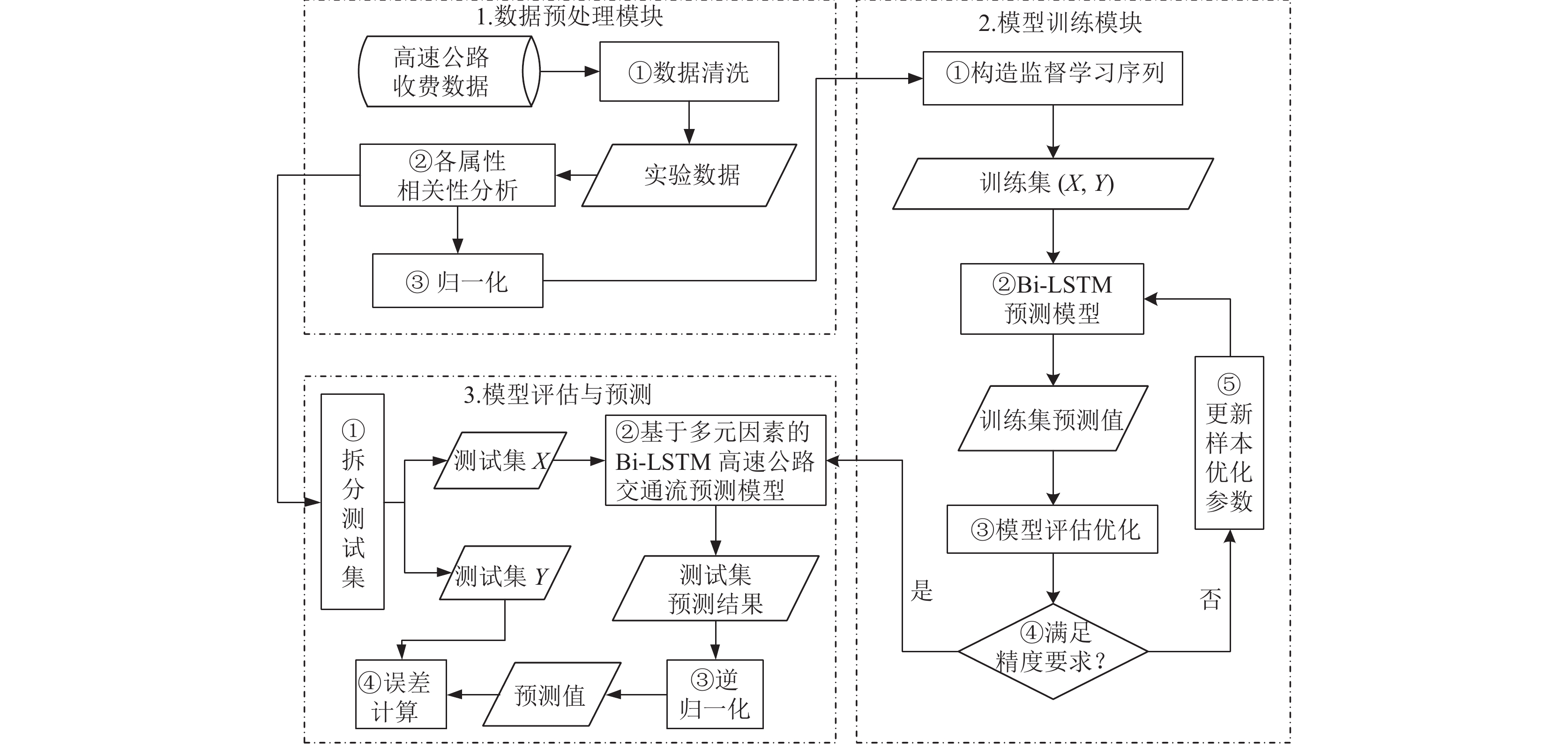
|
图 3 基于多元因素的Bi-LSTM高速公路交通流预测模型 |
3.1.2 相关性分析
经过统计, 共收集到了入站时间, 天气状况, 湿度, 温度, 风速, 风级, 气压, 星期, 是否免费, 节假日, 车流量等多维因素. 为了降低数据维度, 剔除对交通流量影响较小或无影响的因素, 进一步提高基于多元因素的Bi-LSTM高速公路交通流预测模型的准确率, 故采用斯皮尔曼(Spearman)相关系数描述统计变量的相关性, 分析各因素之间的相关关系[19].
对于样本容量为n的样本, n个原始数据被转换成等级数据, 相关系数ρ为:
| ${\rm{\rho }}{\rm{ = }}\frac{{\displaystyle\sum\nolimits_{\rm{i}} {({x_i} - \overline x )({y_i} - \overline y )} }}{{\sqrt {\displaystyle\sum\nolimits_i {{{({x_i} - \overline x )}^2}} \displaystyle\sum\nolimits_i {{{({y_i} - \overline y )}^2}} } }}$ | (2) |
其中,
不同评价指标往往具有不同的量纲和量纲单位, 这样的情况会影响到数据分析的结果, 而且随时刻变化, 交通流量变化较大, 比如凌晨1点的车流量远小于早上8点钟的车流量. 为了消除指标之间的量纲影响以及数据跨度过大的问题, 故选用min-max标准化的方法对数据进行归一化处理. 即对于原数据
对于样本容量为n的样本, n个原始数据被转换成等级数据, 相关系数ρ为:
| ${y_i} = \frac{{{x_i} - \mathop {\min }\limits_{1 \le j \le n} \left\{ {{x_j}} \right\}}}{{\mathop {\max }\limits_{1 \le j \le n} \left\{ {{x_j}} \right\} - \mathop {\min }\limits_{1 \le j \le n} \left\{ {{x_j}} \right\}}}$ | (3) |
得到新序列
高速公路车流量数据以及其他维度的影响因素数据都是时间序列, 在每一个时刻都有一个对应的观测值, 可将实验数据中的时间序列表示为:
| $data = \left[ {\begin{array}{*{20}{c}} {{v_1}({t_1})}&{{v_{\rm{2}}}({t_1})}& \cdots &{{v_{\rm{m}}}({t_1})} \\ {{v_1}({t_2})}&{{v_2}({t_2})}& \cdots &{{v_m}({t_2})} \\ \vdots & \vdots & \cdots & \vdots \\ {{v_1}({t_{\rm{n}}})}&{{v_2}({t_n})}& \cdots &{{v_m}({t_n})} \end{array}} \right]$ | (4) |
其中, m表示观测值的维度个数,
根据斯皮尔曼相关性分析结果, 调整不同维度观测值的权重. 其中,
| $Data \!= \!\left[\! {\begin{array}{*{20}{c}} {{w_{{v_1}}}{v_1}({t_1})}&{{w_{{v_2}}}{v_{\rm{2}}}({t_1})}& \cdots &{{w_{{v_m}}}{v_{\rm{m}}}({t_1})} \\ {{w_{{v_1}}}{v_1}({t_2})}&{{w_{{v_2}}}{v_2}({t_2})}& \cdots &{{w_{{v_m}}}{v_m}({t_2})} \\ \vdots & \vdots & \cdots & \vdots \\ {{w_{{v_1}}}{v_1}({t_{\rm{n}}})}&{{w_{{v_2}}}{v_2}({t_n})}& \cdots &{{w_{{v_m}}}{v_m}({t_n})} \end{array}} \!\right] = \left[\! {\begin{array}{*{20}{c}} {{V_1^m}} \\ {{V_2^m}} \\ \vdots \\ {{V_n^m}} \end{array}} \!\right]$ | (5) |
在训练模型之前, 采用滑动窗口的方式, 通过shift()函数实现窗口的滑动, 将实验数据构建成监督式学习序列:
| $X = \left[ {\begin{array}{*{20}{c}} {V_1^m}&{V_2^m}& \cdots &{V_w^m} \\ {V_2^m}&{V_3^m}& \cdots &{V_{w + 1}^m} \\ \vdots & \vdots & \cdots & \vdots \\ {V_{n - w}^m}&{V_{n - w + 1}^m}& \cdots &{V_{n - 1}^m} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {X_1^{m,w}} \\ {X_2^{m,w}} \\ \vdots \\ {X_n^{m,w}} \end{array}} \right]$ | (6) |
| $Y = \left[ {\begin{array}{*{20}{c}} {{V_{w + 1}}} \\ {{V_{w + 2}}} \\ \vdots \\ {{V_n}} \end{array}} \right]$ | (7) |
其中,
Bi-LSTM模型分别采用前向传输序列和后向LSTM传输序列, 前向LSTM传输序列:
| $a_f^{ < t > } = \overrightarrow {LSTM} ({V_{t - w}},{V_{t - w + 1}} ,\cdots, {V_{t - 1}})$ | (8) |
后向LSTM传输序列:
| $a_b^{ < t > } = \overleftarrow {LSTM} ({V_{t + 1}},{V_{t + 2}} ,\cdots, {V_{t + w}})$ | (9) |
其中,
最后通过
| $\hat {{y^t}} = \sigma ({w_{af}} * a_f^{ < t > } + {w_{ah}} * a_b^{ < t > } + {b_y})$ | (10) |
算法1展示了基于多元因素的Bi-LSTM高速公路交通流预测模型训练的工作流程. 对于每个训练样本, 执行以下算法流程.
算法1. Bi-LSTM网络模型训练算法流程
输入: 训练集数据集Data; 学习率:η.
输出: Bi-LSTM网络模型.
过程:
1. 将训练集X构造成监督学习序列, 并将训练数据集拆分成训练集X和训练集Y;
2. 在(0, 1)范围内随机初始化Bi-LSTM网络中所有权重和偏移量;
3. repeat
4. for all
5. 根据式(7)计算当前样本前向传输序列输出
6. 根据式(8)计算当前样本后向传输序列输出
7. 根据式(9)计算当前样本输出
8. 对比
9. end for
10. until 达到停止条件
3.3 模型预测与评估 3.3.1 模型预测当模型训练好之后, 就可以采用该模型进行交通流的预测. 采用基于多元因素的Bi-LSTM高速公路交通流预测模型进行交通流预测的具体流程如下:
步骤1. 数据准备. 将数据按照Data数组结构构造成
步骤2. 预测. 将步骤1准备的数据输入到训练好的模型中进行预测, 模型会输出一个
步骤3. 逆归一化. 采用inverse_transform()函数对模型输出的矩阵进行逆归一化处理, 得到预测值.
3.3.2 模型评估平均绝对误差MAE (Mean Absolute Error)和均方根误差RMSE (Root Mean Squared Error)是机器学习中评价模型的两把重要标尺, 本次实验选择MAE和RMSE作为模型衡量指标.
| $RMSE = \sqrt {\frac{1}{t}{{\sum\nolimits_{t = 1}^t {\left( {{{\hat y}^t} - {y^t}} \right)} }^2}} $ | (11) |
| $MAE = \frac{1}{t}\sum\nolimits_{t = 1}^t {\left| {{{\hat y}^t} - {y^t}} \right|} $ | (12) |
其中, t表示测试数据集中交通流量观测值对应的观测时刻,
实验计算机配置为: Windows10 64位操作系统, Intel(R) Core(TM) i5-8250U CPU @1.60 GHz 1.8 GHz处理器, 8 GB内存. 程序语言版本Python 3.7.1, 在Keras中以Tensorflow为后端实现的.
4.2 参数设置基于多元因素的Bi-LSTM高速公路交通流预测模型训练中的优化目标是损失函数均方误差MSE最小化, 采用Adam优化算法对网络中涉及的权重进行迭代更新, 从而实现对模型的优化和训练. 模型各参数选用经验数据并通过多次实验进行调整, 最终确定滑动窗口长度为12, 隐含层节点数为52, 学习率为0.001, batch-size为36, 迭代次数Epoch为2000次.
4.3 数据 4.3.1 数据来源数据筛选自陕西省高速公路收费数据, 记录了全年车辆的起终点收费站编号、进出站时间、车辆信息等. 本次实验选取陕西省高速公路流量最大的3个入口站: 六村堡站、灞桥站和三桥站, 筛选这3个站点所有节假日, 包括全年所有周六、周日、法定节假日等时段的车流量数据作为本次实验数据, 考虑到节假日到来前两天车流量逐渐攀升, 在节假日结束后一至两天内流量才开始逐渐回落, 故同时选取节假日前后一至两天的数据.
4.3.2 数据分析对预处理后的数据进行相关性分析. 分别计算各因素与交通流量的斯皮尔曼相关系数, 详细数据见表1.
| 表 1 各因素与交通流量的斯皮尔曼相关系数 |
分析可知, 入站时间、温度、风速、星期和交通流之间的相关系数值分别为0.124、0.354、0.242、0.150, 并呈现出0.01水平的显著性, 因而说明入站时间、温度、风速、星期和交通流量之间有着显著的正相关关系. 湿度、气压、是否免费和交通流量之间的相关系数值分别为−0.349、−0.152、−0.446, 并且呈现出0.01水平的显著性, 因而说明湿度、气压、气压和交通流量之间有着显著的负相关关系. 除此之外, 天气状况与交通流量之间的相关关系数值并不会呈现出显著性, 意味着天气状况与交通流量之间并没有相关关系.
结合实际实验数据, 本次实验数据是全年周六、周日、法定节假日数据, 其中并未出现大雾、大雪等严重影响交通流量的恶劣天气, 故结合斯皮尔曼分析结果判定天气维度不属于本次实验的有效信息, 删除后既可降低数据维度, 又不会影响整体实验数据信息的完整性.
4.4 误差分析根据斯皮尔曼相关分析的结果, 实验数据选用入站时间、温度、湿度、风速、气压、星期、是否免费、节日和交通流量等9个因素. 采用基于多元因素的Bi-LSTM高速公路交通流预测模型分别对3个站点(灞桥站、六村堡站、三桥站)的车流量数据以5 min, 10 min, 15 min, 30 min, 60 min 5种时间粒度分别进行预测, 其中, 每组数据的前80%做训练集, 后20%做测试集, 所测日期均为节假日. 图4展示了3种模型的预测结果与真实值对比产生的误差. 可见, 无论从RMSE、还是从MAE来看, 当对同一站点以相同时间粒度进行预测时, Bi-LSTM模型预测结果的实验误差总小于GRU模型和LSTM模型, 表现出了良好的适用性, 并在15 min时间粒度时, 误差最小. LSTM模型和GRU模型均在5 min时间粒度时取得最小误差. 其中GRU模型的预测误差随时间粒度的减小而减小, 更适合做短期预测.
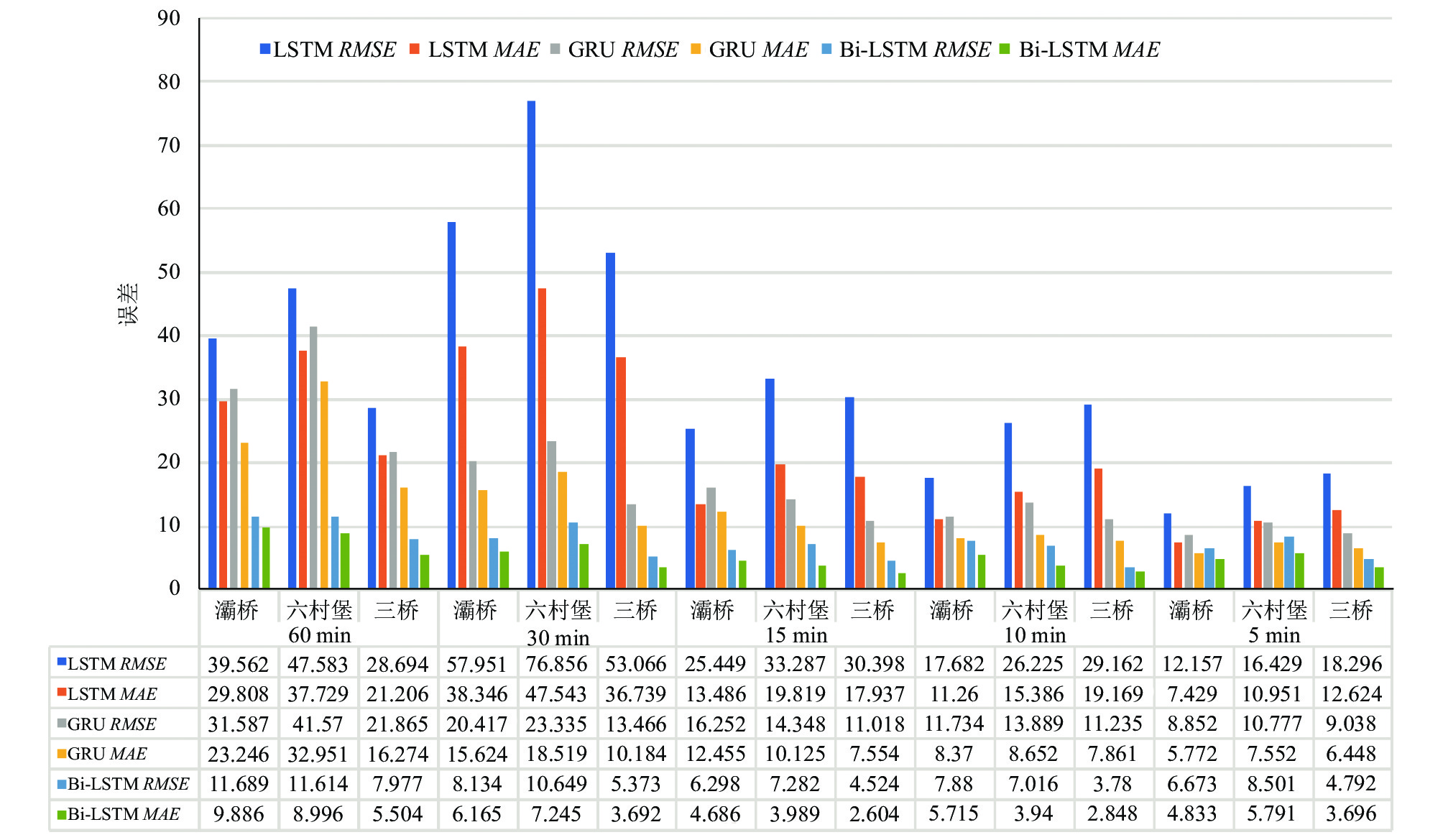
|
图 4 3种模型对不同时间粒度的实验误差 |
为了更清晰展示预测效果, 分别选取12月28日3个站点15 min时间粒度的预测结果进行展示. 对比图5~图7可以看出LSTM、GRU和Bi-LSTM都可以很好的预测出车流量的变化趋势, 但是LSTM对高峰期时变化幅度较大的部分预测效果比较差, 会出现预测滞后情况, GRU对高峰期和低峰期时预测效果波动比较大. 整体而言, Bi-LSTM的预测值更贴合真实值. 说明基于多元因素的Bi-LSTM高速公路交通流预测模型在短期交通流预测中的预测效果优于LSTM模型和GRU模型.
5 结论本文应用斯皮尔曼相关系数对交通流与天气状况、节假日、收费情况的相关性进行分析, 在确定温度、湿度、风速、风级、气压、星期、是否免费、节日类型和交通流具有相对较强相关性的情况下, 构建了一种基于多元因素的Bi-LSTM高速公路交通流预测模型, 该模型可以根据历史数据和当前天气、节假日及收费情况对当前交通流量进行更准确的预测.

|
图 5 灞桥站点 |
实验采用Bi-LSTM预测模型对不同站点、不同时间粒度的交通流量进行预测, 通过对比GRU和LSTM两种循环神经网络, 表明基于多元因素的Bi-LSTM高速公路交通流预测模型在高速公路短期交通流量预测中适用性更强、精确度更高.
影响车流量的因素多种多样, 目前只考虑了天气、节假日、收费情况3个方向, 交通事故、交通管制等对短期交通流量也有显著的影响. 在以后的研究中, 可考虑从这几个方面进行研究, 进一步提高交通流量预测的准确率.
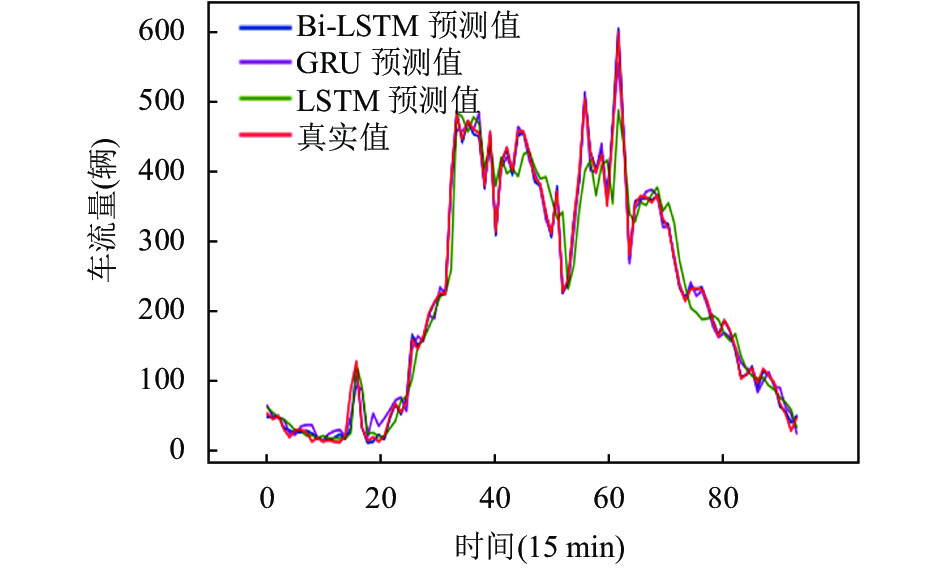
|
图 6 六村堡站点 |

|
图 7 三桥站点 |
| [1] |
Alam I, Farid DM, Rossetti RJF. The prediction of traffic flow with regression analysis. Abraham A, Dutta P, Mandal JK, et al. Emerging Technologies in Data Mining and Information Security. Singapore: Springer, 2019. 661–671.
|
| [2] |
刘艳丽, 赵卓峰, 丁维龙, 等. 基于高速收费大数据的短时交通流量预测方法. 计算机与数字工程, 2019, 47(5): 1164-1169, 1188. DOI:10.3969/j.issn.1672-9722.2019.05.029 |
| [3] |
Ye RZ, Zhang YL, Middleton DR. Unscented Kalman filter method for speed estimation using single loop detector data. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1968(1): 117-125. DOI:10.1177/0361198106196800114 |
| [4] |
Okutani I, Stephanedes YJ. Dynamic prediction of traffic volume through Kalman filtering theory. Transportation Research Part B: Methodological, 1984, 18(1): 1-11. DOI:10.1016/0191-2615(84)90002-X |
| [5] |
杨立才, 贾磊, 何立琴, 等. 基于混沌小波网络的交通流预测算法研究. 山东大学学报(工学版), 2005, 35(2): 46-49, 98. DOI:10.3969/j.issn.1672-3961.2005.02.011 |
| [6] |
王正武, 黄中祥. 短时交通流预测模型的分析与评价. 系统工程, 2003, 21(6): 97-100. DOI:10.3969/j.issn.1001-4098.2003.06.020 |
| [7] |
杨凡, 严忠贞. 混合神经网络挖掘模型在交通流量预测中的研究. 小型微型计算机系统, 2012, 33(9): 1978-1981. DOI:10.3969/j.issn.1000-1220.2012.09.021 |
| [8] |
Li LC, He SL, Zhang J, et al. Short-term highway traffic flow prediction based on a hybrid strategy considering temporal-spatial information. Journal of Advanced Transportation, 2016, 50(8): 2029-2040. DOI:10.1002/atr.1443 |
| [9] |
Du SD, Li TR, Gong X, et al. Traffic flow forecasting based on hybrid deep learning framework. Proceedings of 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE). Nanjing, China. 2018. 1–6.
|
| [10] |
沈凌, 陆建, 邓翎, 等. 基于收费数据的高速公路短时客货运输量短时预测研究. 第十四届中国智能交通年会论文集. 青岛, 中国. 2019. 9.
|
| [11] |
周桐, 杨智勇, 孙棣华, 等. 分车型的高速公路短时交通流量预测方法研究. 计算机应用研究, 2015, 32(7): 1996-1999. DOI:10.3969/j.issn.1001-3695.2015.07.020 |
| [12] |
Zhang D, Kabuka MR. Combining weather condition data to predict traffic flow: A GRU based deep learning approach. IET Intelligent Transport Systems, 2018, 12(7): 578-585. DOI:10.1049/iet-its.2017.0313 |
| [13] |
蔡延光, 乐冰, 蔡颢, 等. 暴雨天气下高速公路短时交通流预测. 计算机工程, 2020, 46(6): 34-39. |
| [14] |
Ma XZ, Hovy E. End-to-end sequence labeling via Bi-directional LSTM-CNNs-CRF. Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics. Berlin, Germany. 2016. 1064–1074.
|
| [15] |
钟晨昊, 王蒙, 赵威, 等. 基于LSTM的平面交叉口短时交通流预测. 公路交通技术, 2019, 35(5): 119-123, 131. |
| [16] |
Alkhwiter W, Al-Twairesh N. Part-of-speech tagging for Arabic tweets using CRF and Bi-LSTM. Computer Speech & Language, 2021, 65: 101138. |
| [17] |
刘飞龙, 郝文宁, 陈刚, 等. 基于双线性函数注意力Bi-LSTM模型的机器阅读理解. 计算机科学, 2017, 44(S1): 92-96, 122. |
| [18] |
张子睿, 刘云清. 基于BI-LSTM-CRF模型的中文分词法. 长春理工大学学报(自然科学版), 2017, 40(4): 87-92. |
| [19] |
Spearman C. The proof and measurement of association between two things. International Journal of Epidemiology, 2010, 39(5): 1137-1150. DOI:10.1093/ije/dyq191 |
 2021, Vol. 30
2021, Vol. 30



