机器人在对目标物体进行自动抓取之前, 首先应确定被抓物体的位姿, 即确定合适的抓取位置及抓取姿态, 而机器视觉检测是最常用的目标位姿检测方法. 典型的机器视觉位姿提取方法主要包括单目视觉和双目视觉^[1]两大类. 单目视觉操作方便, 处理数据信息速度快, 但缺乏深度信息, 难以完成测量深度的工作; 双目视觉利用空间同一点在两个摄像机上成像点的匹配, 可以进行深度测量, 并可以对简单环境中的形状简单的物体定位定姿, 它的缺点是计算过程涉及大量的图像匹配和目标识别算法, 只能针对具有简单几何关系的目标使用, 无法在复杂背景下应用. 本文研究是基于二维平面坐标系下进行位姿检测, 因此使用单目视觉更为简单方便.

单目视觉采集完图像, 图像需预处理, 在图像匹配研究成果中, 贾迪等^[2]对从局部不变特征点、直线、区域匹配3个方面对图像匹配方法予以综述, 其中局部不变特征点是图像匹配中发展最早也比较成熟的图像方法, 以SIFT的改进算法SURF不变特征点在图像匹配中更为常见, 图像匹配效果相对较好; 林志东等^[3]对特定条件下SIFT与SURF图像匹配算法的性能进行了对比实验, 特征点提取方面, SURF算法运算速度更快, 而SIFT算法能提取出更多的特征点; 特征匹配方面, SIFT算法在图像存在光照差异时具有更大的优势, SURF算法在处理有视角差异的图像时稳定性更好. 在位姿测量中, 徐昌源等^[4]提出了改进最小二乘法的双目视觉位姿测量技术研究与测试的方法, 该测量方法虽效果佳, 但仅适用于双目视觉位姿测量的数学模型中; 谷凤伟等^[1] 设计出一种简易的单目视觉位姿测量方法, 但需要将一种精确的靶标检测算法与单目视觉测量方法相结合, 才能实现机器人位姿的测量, 由于该精确的靶标也需要图像处理和检测, 在计算过程中难免会造成误差积累. 在视觉伺服过程中, 徐德^[5]对单目视觉在视觉伺服研究中进行了综述, 分析了不同视觉伺服方法的特点及典型应用, 认为混合视觉伺服(基于位置的视觉伺服和基于图像的视觉伺服)在未来有很大的发展前景, 但目前, 基于图像的视觉伺服仍是当前研究的热点; 陈梅等^[6]针对无标定视觉伺服系统eye-in-hand型结构, 提出一种以图像特征为反馈的模糊控制策略, 对平面内运动物体进行跟踪, 该eye-in-hand型结构为视觉伺服奠定了一定的基础, 伺服效果相对较好, 但其反馈的模糊控制系统相对比较复杂.

针对以上文献中的图像处理算法与视觉伺服问题, 本文提出一种相机在机械臂上eye-in-hand型视觉伺服抓取手机策略, 选取SURF不变特征点匹配算法进行目标检测, 以及对二维坐标系下目标图像进行最佳位姿解算, 为伺服机械臂抓取手机提供准确性.

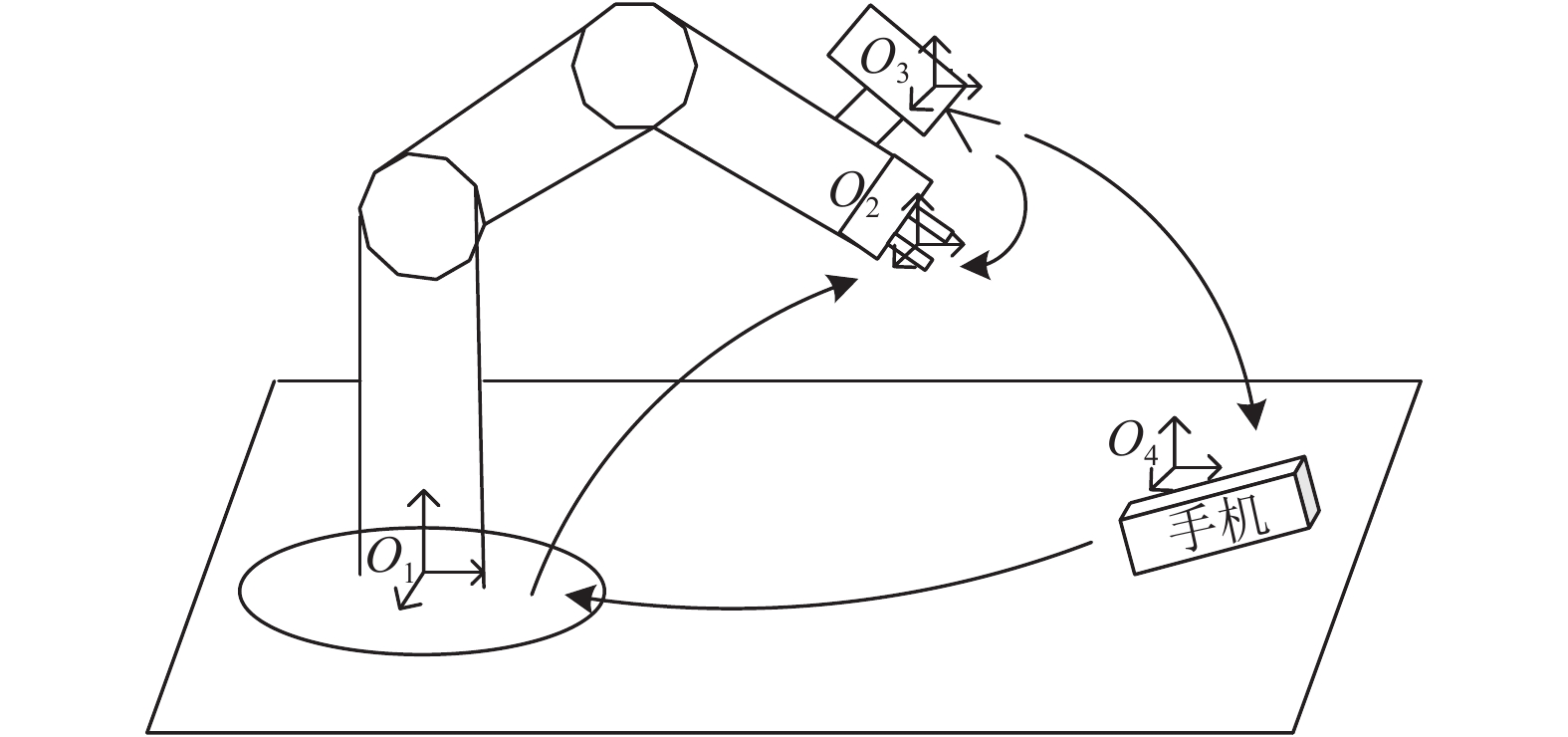
1 视觉伺服手机抓取策略

针对特殊环境手机拾取问题, 本文采用一种基于视觉伺服的机械臂方案, 即采用相机搜索手机, 然后引导机械臂进行抓取. 机械臂与相机位置一般有两种关系: 一种相机在机械臂上eye-in-hand, 这种可操作性高并且可以获取较高的图像数据; 一种是相机在机械臂外eye-to-hand, 其优点是相机获取的视野广、灵活性强, 但机械臂易受相机的位置影响. 本文采用相机在机械臂上eye-in-hand, 经过相机与机械臂末端执行器的标定之后可以获得固定的变换关系, O₁O₂O₃O₄分别表示机械臂坐标系、机械手抓坐标系、相机坐标系、手机坐标系的原点. 该方案原理如图1所示.

用机械臂抓取手机方法步骤为: 第1步: 利用标定好的相机对掉进沟缝中的手机进行采样; 第2步: 将采样到的图像进行图像预处理, 并进行目标检测; 第3步: 将处理好的图像, 即采集到手机的目标状态, 进行手机位姿检测; 第4步: 将检测到手机的最佳位姿进行解算, 并伺服控制机械臂对手机进行抓取. 在抓取过程中, 抓取的准确性、安全性、适应性主要依赖于手机目标检测和位姿解算, 使机械臂及手抓按最佳方案进行抓取.

2 位姿检测方法

位姿检测是伺服机械臂抓取手机的关键, 位姿检测前对相机标定是采集图像的必要条件, 是减小误差, 提高相机匹配速度的重要步骤. 位姿检测方法包括SURF不变特征点匹配进行目标检测, 以及二维坐标系下的最佳位姿解算.

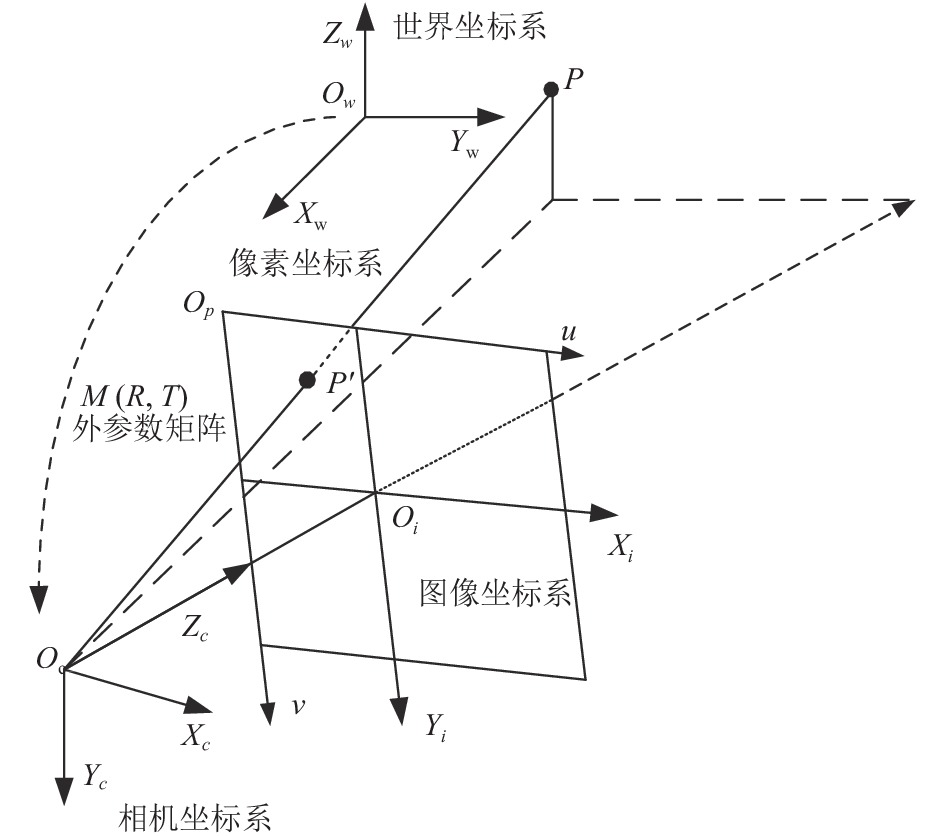
2.1 相机成像原理及相机标定

相机成像模型主要由世界坐标系O_w-X_wY_wZ_w, 相机坐标系O_c -X_cY_cZ_c、像素坐标系O_p-u v 、图像坐标系O_i-X_iY_i构成, P是相机坐标系中的一点, 其坐标是(X_c, Y_c, Z_c), P′是在图像中的成像点, 在图像坐标系的坐标是(x, y), 在像素坐标系是(u, v). 成像原理模型如图2所示.

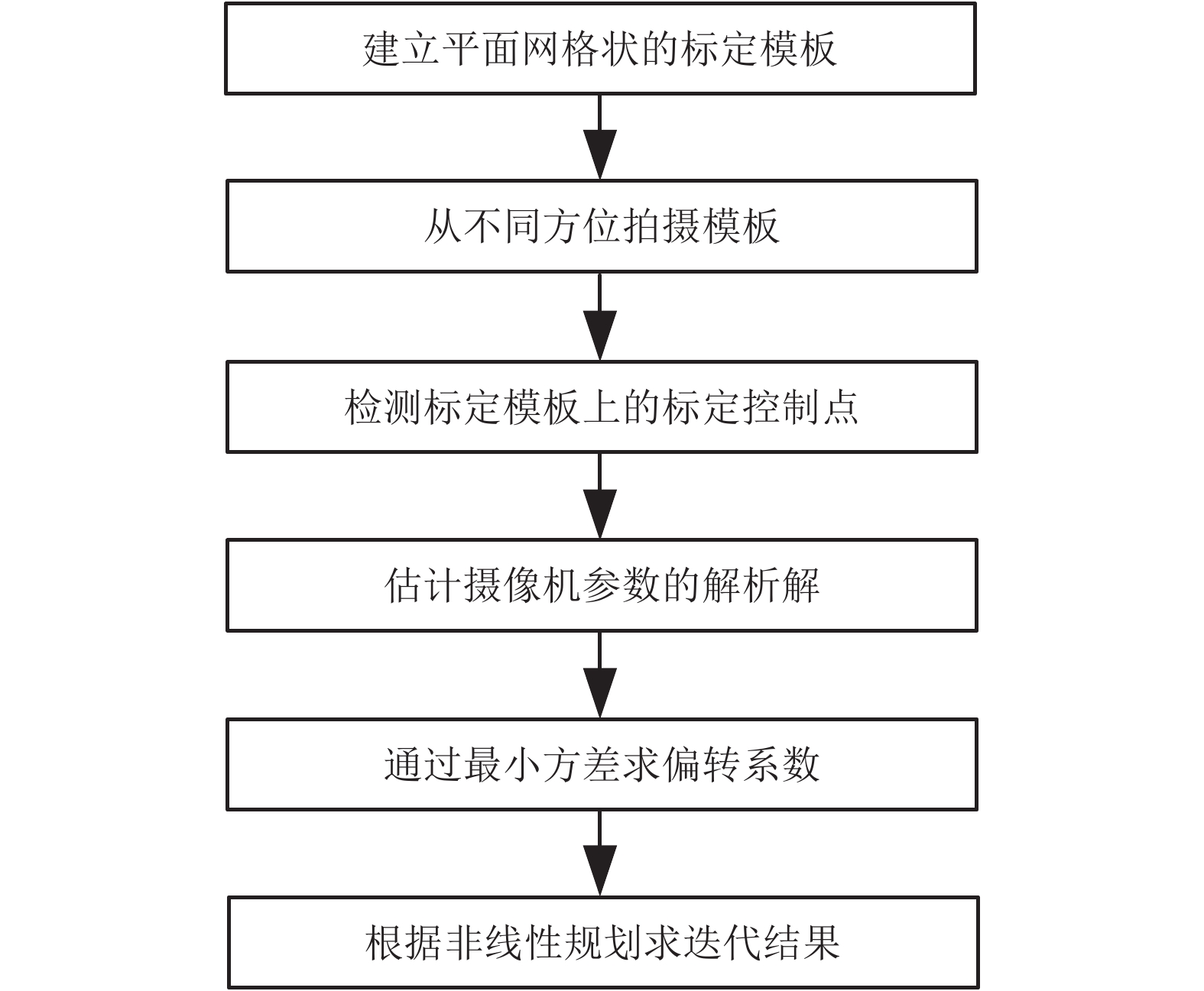
相机标定是为了确定相机坐标系、图像坐标系、像素坐标系与真实坐标系之间的关系, 具体而言即由相机的成像原理创建数学模型, 借助已知特征的像素坐标和对应的世界坐标推导相机的模型参数^[7]. 通过张正友对相机的内外参数进行标定. 张正友标定流程, 如图3所示.

利用相机标定结果和单目摄像头成像原理完成相机成像过程的坐标系变换. 确定物体相对于相机坐标系的位姿, 进而确定相对于机械臂的位姿, 相机标定结果可以求出相机的内外参数矩阵, 相机的内参数矩阵是唯一, 而外参数矩阵不唯一^[1]. 内参数矩阵对位姿解算在视觉伺服机械臂具有重要的意义.

2.2 SURF不变特征点匹配算法

SURF算法^[3]在提取特征点时, 主要包含以下6个步骤.

步骤1. 建立积分图像. 通过简单的加减法去计算任一区域的像素之和. 如图4所示, 矩形ABCD内所有像素的灰度值之和计算公式为:

$ \sum = {{A - B - C + D}} $

(1)

步骤2. 建立Hessian矩阵. 一个像素点(x, y), 设函数 f(x, y)的Hessian矩阵定义为:

$H(x,y) = \left[ {\begin{array}{*{20}{c}} {{L_{{{xx}}}}(x,\sigma )}&{{L_{{{xy}}}}(x,\sigma )} \\ {{L_{{{xy}}}}(x,\sigma )}&{{L_{yy}}(x,\sigma )} \end{array}} \right]$

(2)

可以看出H矩阵由函数f的二阶偏导数构成, 每一个像素点都可以解算出一个H矩阵. 式中, ${L_{xx}}(x,\sigma )$ 为图像f与尺度为σ的高斯二阶导数的卷积其定义如下:

${L_{xx}}(x,\sigma ) = \frac{{{\partial ^2}}}{{\partial {x^2}}}g(\sigma ) * f$

(3)

对于 ${L_{x{{y}}}}(x,\sigma )$ 和 ${L_{{{yy}}}}(x,\sigma )$ , 定义相似.

步骤3. 建立尺度空间. SUFR特征极值点的检测算法和提取是基于尺度空间理论. 通过改变使用高斯滤波器的尺度, 不是改变图像本身来构成对不同尺度的响应.

步骤4. 提取特征点. 利用非极值去除掉确定特征点, 在海森行列式图像的每个像素点与3维邻域的26个点进行大小比较, 设定一个阈值, 用3维线性插值法得到亚像素级的特征点后, 去掉特征值小于阈值的点, 得出更稳定的点.

步骤5. 选取特征点的方向. 以特征点为中心, 检测兴趣点确定尺度s, 统计半径扇形内所有点的Haar小波响应, 并给靠近特征点的像素赋予较大的权重. 统计该区域所有Harr小波响应之和, 形成矢量, 即扇形的方向. 遍历所有的扇形区域, 选择最长矢量方向作为该特征点的方向.

步骤6. 构造SURF的特征点描述子. 以特征点为中心, 构造出以20s为边长的正方形窗口, s为特征点所在的尺度. 将其分为16个4×4的子区域, 每个子区域统计包含有25个像素元的水平x和垂直y的Haar小波特征之和分别为 $\displaystyle\sum {{H_{{x}}}} $ 和 ${\displaystyle\sum {{H_{{y}}}} }$ . 统计出每个子区域的4维描述子V= $\left[ {\displaystyle\sum {{H_{{x}}}} } \right.$ , ${\displaystyle\sum {{H_{{y}}}} }$ , ${\displaystyle\sum {\left| {{H_{{x}}}} \right|} }$ , $\left. {{\displaystyle\sum {\left| {{H_{{y}}}} \right|} }} \right]$ . 得出特征向量长度为64维的特征描述子.

2.3 最佳位姿检测 2.3.1 算法原理

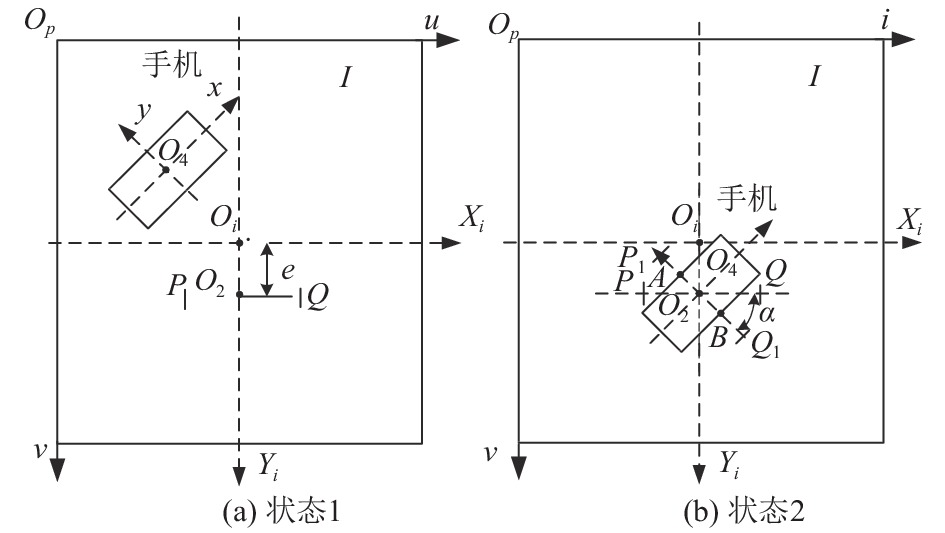
手机的最佳位姿检测包括SURF不变特征点匹配的目标检测和其位姿解算. 对机械臂上相机标定完, 解出相机的内外参数矩阵, 对SURF不变特征点匹配检测到手机图像在二维坐标系下进行最佳位姿检测与解算, 解算原理过程如图5所示.

原理过程如下: 在图像坐标系O_i-X_iY_i中, 设手机的质心坐标为O₄(s_x,s_y), 设机械臂末端手抓中心O₂(z_x,z_y)与相机光轴中心O_i所标定的偏差距离e, 标定机械手抓的手指姿态为PQ, 与相机的成像的投影关系如图5(a)所示, 其中O_p-u v 是像素坐标系.

伺服机械臂从图5(a)移动至图5(b)状态, 使其手抓的中心O₂与手机的质心O₄重合, 如图5(b)所示. 手机姿态的y轴与图像坐标系O_i-X_iY_i的X_i轴夹角是 $\alpha $ , 手机不动, 驱动机械手抓旋转 $\alpha $ 角度, 使其手指PQ与手机姿态的y轴在投影上重合, 即机械手抓旋转 $\alpha $ 角度后手指PQ的新姿态为P₁Q₁, 抓取点为A(x₁, y₁)和B(x₂, y₂)两点. 旋转角度 $\alpha $ 和手指的新姿态P₁Q₁为伺服机械臂抓取手机提供了准确性.

2.3.2 算法设计

位姿解算是将图像在像素坐标系O_p-u v 中位置关系转化为图像的物理坐标O_i-X_iY_i, 其目的是在图像的物理坐标系中可以进行几何关系的计算, 转化公式为矩阵形式(4)^[1]:

$\left[ {\begin{array}{*{20}{c}} {{u}} \\ v \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{dx}}}&0&{{u_0}} \\ 0&{\dfrac{1}{{dy}}}&{{v_0}} \\ 0&0&1 \end{array}} \right]\;\;\;\;\left[ {\begin{array}{*{20}{c}} x \\ y \\ 1 \end{array}} \right]$

(4)

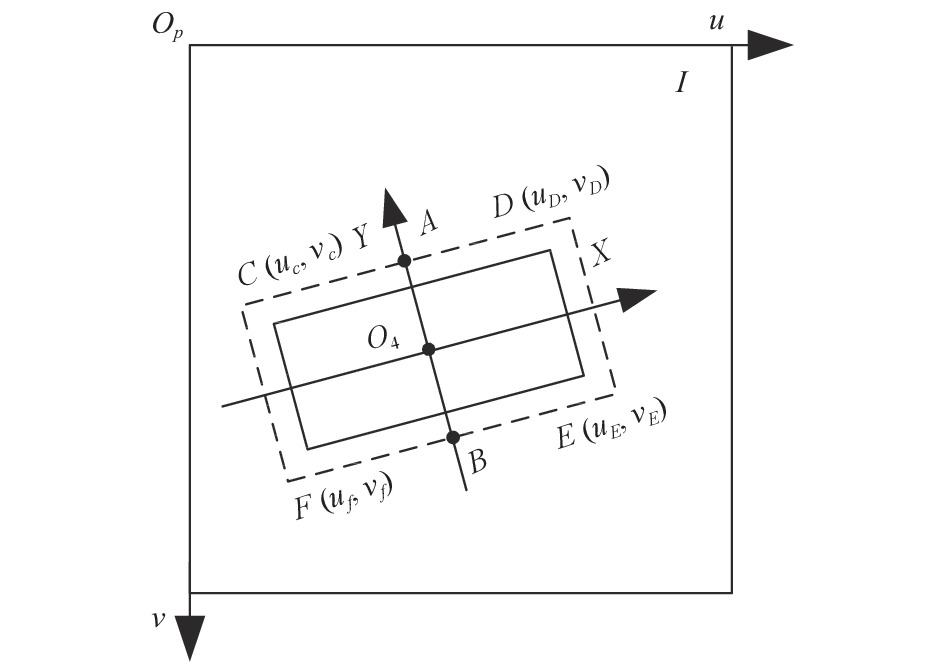
其中, (u, v)是在水平方向上和垂直方向的像素, 设O_i(u₀, v₀)是图像的坐标系中心的像素, dx和dy是每个像素在x轴和y轴的方向上的实际物理尺寸, 由相机的标定可以知u₀, v₀, dx, dy. SURF不变特征点算法匹配到的手机矩形框CDEF中利用图像算法可求出手机的质心O₄(u_s, v_s)和CDEF的像素坐标, 根据几何关系进而可以求出手机的抓持点A(u₁, v₁)和B(u₂, v₂)的像素坐标, 其匹配到的手机矩形框, 如图6所示.

将手机的抓持点A(u₁, v₁)和B(u₂, v₂)的像素坐标带入式(4)推导可得A和B的物理坐标, 如式(5)和式(6):

$\left\{ {\begin{array}{*{20}{c}} {{{{x}}_1} = dx\left( {{u_1} - {u_0}} \right)} \\ {{{{y}}_1} = dy\left( {{v_1} - {v_0}} \right)} \end{array}} \right.$

(5)

$\left\{ {\begin{array}{*{20}{c}} {{{{x}}_2} = dx\left( {{u_2} - {u_0}} \right)} \\ {{{{y}}_2} = dy\left( {{v_2} - {v_0}} \right)} \end{array}} \right.$

(6)

所求出A(x₁, y₁)和B(x₂, y₂)的图像物理坐标, 可以解出夹角 $\alpha $ 即最佳位姿角, 理论上伺服给机械手抓的旋转角度也应为 $\alpha $ , 但由于机械臂的系统误差使得旋转角度小于或大于 $\alpha $ , 故取旋转角度为 $\;\beta $ . 取机械手抓相对手机顺时针旋转为正, 逆时针旋转为负, 利用在坐标系中由两点之间的几何关系可求其斜率, 可得式(7):

$\alpha {{ = \arctan}}\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

(7)

由式(5)~式(7)可得式(8):

$\alpha {{ = \arctan}}\frac{{{{dy}}({v_2} - {v_1})}}{{dx({u_2} - {u_1})}}$

(8)

求出式(8)中的角度 $\alpha $ , 取值范围[0, 90°], 若 为正则机械手抓顺时针旋转, 负则逆时针旋转. $\alpha $ 是手机在二维平面的位姿角也是机械手抓旋转的夹持角, 其夹持点为A和B两点. 由式(8)可知, dx, dy 是相机内参数, 故 $\alpha $ 只与夹持点A和B两点的像素点的差值有关, 简化了图像中复杂的计算, 从而提高视觉伺服效果.

从算法的设计原理和求解结果来看, 相比传统的位姿检测算法, 在计算上有较大的改进. 如最早由Fischler等于1981年提出典型PNP问题^[8], 是其根据目标点的图像坐标和相机成像模型解算目标相对于相机的位姿问题, 而在其平面PNP问题的求解过程中会用到非线性求解算法, 该算法虽法精度较高, 但一般需要迭代, 计算量较大, 且存在稳定性问题. 而在后期的研究深入过程中如典型的算法有Oberkampf^[9]提出的POSIT算法; Schweighofer^[10] 提出的平面目标位姿估计算法(SP); Lepetit等^[11]提出的EPnP算法, Lu等^[12]提出的正交迭代算法等. 这些典型算法在位姿求解过程中都属于非线性求解, 因此会占用图像解算过程中的资源问题, 而本算法的提出可以良好的避免复杂的迭代问题, 减少占用资源问题.

2.4 算法实现步骤

具体过程如下:

(1)读取照片;

(2)提取SURF特征点;

(3)根据特征点生成图像的特征向量;

(4)初步建立一个匹配对(含野值);

(5)预测仿射变化, 去除不满足变化的野值;

(6)获取目标物的多边形框;

(7)二维坐标系下其最佳位姿解算;

(8)伺服控制机械臂抓取手机.

3 实验及分析

相机标定和目标检测实验选用Matlab 2018b版软件, 以及Matlab硬件支持包usbwebcams, 操作系统为64位Win 10系统. 位姿解算与伺服机械手抓抓取实验选用Rethink双臂机器人的右臂, 其操作系统为64位Linux系统Ubuntu 16.04, 进行抓取验证.

Rethink双臂机器人的右臂进行位姿检测和手机抓取实验之前需要先完成以下4点: (1) 右臂上相机的内外参数的标定; (2) 手抓中心与相机中心的位置校正; (3) 将双臂机器人的UI显示界面窗口大小标定为640×480像素; (4) 右臂末端初始位置的标定, 使其在沿水平面方向移动搜索^[13-16].

3.1 相机标定实验

机械臂上的摄像头最大分辨率为1280×800像素的摄像头, 标定板为10×7的棋盘格, 各格边长28 mm×28 mm, 其采集20张像素尺寸为480×640图片, 导入到Matlab工具箱中进行摄像机标定^[17,18].

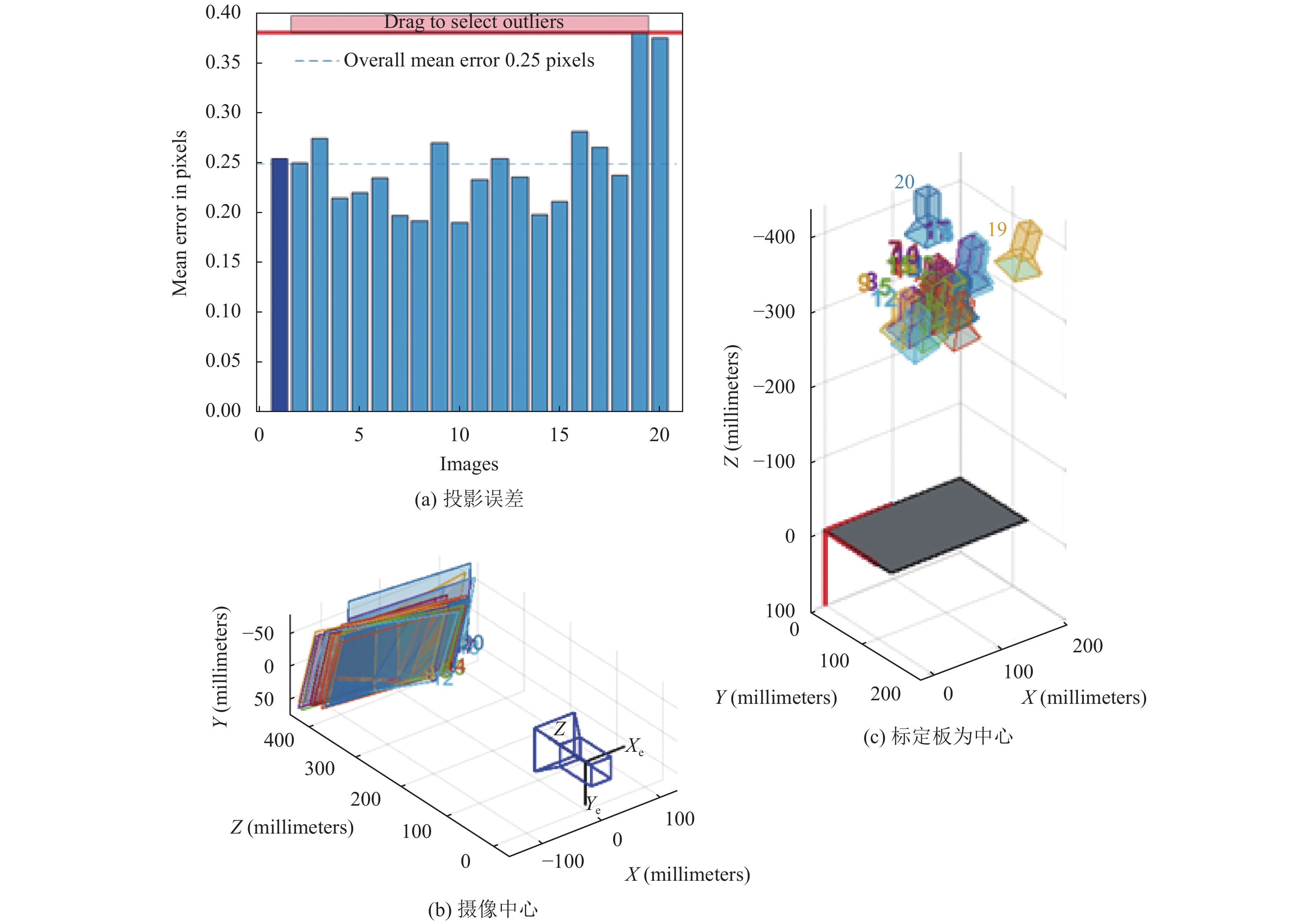
Matlab工具箱标定实验中, 需对相机标定结果进行评估, 可以通过相机的投影误差分析、以摄像机为中心和以标定板为中心的三维外部参数可视化进行分析, 标定过程具体如图7所示.

在Matlab工具箱标定实验后, 在其命令行中输入cameraParams.IntrinsicMatrix, 可以求出相机内参数矩阵, 输入RadialDistortion和TangentialDistortion可以求出相机的径向畸变和切向畸变系数^[19,20], 具体相机的物理参数如表1所示.

3.2 SURF特征点目标检测与位姿解算实验

为了验证提出算法对伺服机械臂抓取手机的有效性, 完成位姿检测实验, 该实验包括SURF不变特征点的目标检测实验和位姿解算实验. 同时为使实验更具说服力, 笔者完成单一背景下和复杂背景(没有遮挡)下的两组位姿检测对比实验, 观察复杂背景下是否会影响位姿检测的算法实验效果. 分别取五组单一背景和五组复杂背景下的位姿检测实验的实验结果进行分析对比及评价, 实验结果分析表, 如表2所示. 单一背景下位姿检测实验过程和复杂背景下位姿检测实验过程, 如图8和图9所示.

实验表明, 单一背景中的SURF不变特征点提取的特征点数相对较多, 但易出现交叉点; 复杂背景中的提取的特征点数虽较少, 但出现的交叉点也较少; 二者在特征点匹配的正确率、匹配时间上相当, 在匹配效果上单一背景的总体稍好于复杂背景, 但从整体的实验结果而言, 复杂背景下该算法可以满足检测到手机. 无论是在单一背景下还是在复杂背景下, 其SURF不变特征点匹配实验的特征点匹配速度和效果都相对准确稳定, 并且可以匹配到手机在o-xy平面上的任意偏转角度, 即手机在二维平面上的位姿, 利用图像算法和提出的位姿解算算法可以求解出两个理论的机械手指夹持点A和B, 进而得到位姿角 $\alpha $ .

通过手机的抓取实验来验证解算出的位姿角 $\alpha $ 的准确性, 其中抓取实验是以手抓为参考对象, 取顺、逆时针手机状态各6张, 其像素尺寸为640×480像素, 是其在复杂背景下的二维坐标系的位姿状态. 由相机标定实验和SURF特征点匹配实验可求出相机的内参数u₀, v₀, dx, dy及机械手抓抓取手机的两个夹持点A和B, 代入式(8)解出最佳位姿角 $\alpha $ , 即机械臂末端手抓应旋转角度 $\;\beta $ . 解算出的位姿角 $\alpha $ 和机械臂末端手抓旋转的角度 $\;\beta $ 存在一定的误差, 为验证该误差是否会影响手机抓取, 列出位姿角与手抓旋转角度误差分析表, 如表3所示.

在表3中, 位姿角 $\alpha $ 与输出给机械手抓旋转角度 $\;\beta $ 存在一定的误差, 分析出主要误差来源是双臂机器人机械臂的末端手抓中舵机旋转的精度, 该舵机的旋转精度只能精确到0.1位, 属于系统的绝对误差, 其不可避免; 经过实验抓取发现其相对误差来源于光线、手机表面的纹理等. 实验抓取过程中发现, 误差小于1~2°, 不影响手机的抓取. 为避免机械臂在抓取中出现碰撞, 笔者先在PC端仿真抓取手机模拟, 最后将编译的代码下载到双臂机器系统中. 选取的12组手机抓取实验, 良好的验证了提出算法的有效性, 为视觉抓取提供了准确性. 位姿解算与抓取手机实验, 如图10所示.

4 结论与展望

本文提出一种二维平面坐标系下利用单目视觉系统测量手机的最佳位姿检测算法, 该算法将单目视觉与伺服机械臂相结合, 通过相机标定, 图像采集、图像预处理等过程, 实现SURF不变特征点匹配到目标物体, 完成目标检测. 通过摄像机成像原理, 计算出从像素坐标系到图像坐标系的位置变换关系, 利用两点间求斜率的几何关系进而求出目标物体的最佳位姿角, 即伺服机械手抓应旋转的角度, 本算法简单易行, 可有效避免双目视觉位姿测量过程中图像匹配资源占用问题. 实验验证了该算法的有效性和准确性, 可以完成手机最佳位姿检测及机械手抓持点的确定, 满足视觉伺服机械臂抓取要求. 同时, 该测量算法可以应用到工业零件定位、码垛机器人搬运等领域, 具有广阔的应用前景.