在中国, 很多地区的冬季温度都在0度左右, 并且随着电动汽车在国内的普及, 其核心部件锂电池的低温特性应该满足在特定环境下的使用要求. 如何在低温状态下实时显示估计锂电池的实时容量对与电池状态管理至关重要. 电动汽车动力电池组荷电状态(State Of Charge, SOC)、电池组健康状态(State Of Health, SOH)、放电深度(Depth Of Discharge, DOD)、能量状态(State Of Energy, SOE)、剩余寿命(ResidUal Life, RUL)等电池管理系统(Battery Management System, BMS)参数对锂电池实施运行状态分析起到支撑作用[1]. 如何精准预测电动汽车锂电池实时荷电状态对电池状态管理, 电池寿命, 电池的保护是至关重要的, 正确的电动汽车锂电池实时荷电状态精准预测应用在电动汽车产业领域上能够大大提升电动汽车电池的安全性以及寿命. 因此, 准确的预测电池的荷电状态SOC有利于推动电动汽车技术的进步. 电池的SOC与电池两端的电压, 充放电时电池的瞬态电流, 电池的温度, 电阻, 电池的实验工况有关. 如何在每个瞬时精准预测在当前电流电压下的电池实时SOC是工业界上一大难题. BP具有较强的非线性映射能力, 以及有不错的非线性泛化能力, 但在网络层数增加时容易陷入局部最小以及梯度离散的情况[2]. 传统的 BP神经网络解决的是一个复杂非线性化问题, 神经网络的权值大小是通过沿局部改善的方向逐渐进行调整的, 这样会使算法陷入局部极值, 权值收敛到局部极小点, 从而导致网络训练失败. 有效设计BP神经网络能够加强对学习率的约束、对梯度的影响以及减少训练损失. 王晨等[3]基于粒子群优化神经网络估算动力电池SOC, 结果显示该方法具有较高的精度以及收敛速度, 并且粒子群优化算法缺乏速度的动态性调节, 容易陷入局部最优, 不易收敛精度低, 参数控制也较为困难. 因此在这里提出了基于HPPC实验工况数据为基础的一种构建以全连接层为基底的, 选取Nadam优化算法以及Log-cosh损失函数的网络模型构建方法.
1 深度前馈网络总体架构设计深度前馈网络设计的难点在于如何确定不同层所具有的单元数, 以及单元间的连接方式. 深度前馈神经网络, 以输入层, 隐藏层, 输出层为基础网络架构, 通过损失函数度量真实值与预测值之间的损失, 进一步通过梯度下降法求取权重系数矩阵W与偏倚向量b. 测试样本通过输入层传入所获得的逼近函数, 输出测试结果. 图1为对深度神经网络化模型基础构架模糊化描述, 将输入简化为电流电压, 每两层的节点采用全连接的方式, 共有L层网络层, 输出节点为SOC,
针对实验工况数据进行深度神经网络化模型基础构架具体化构建.
基于图1所示全连接型深度神经网络化模型模糊化基础构架, 本文以锂电池的电压U和电流I以及时间节点T为输入, 电荷状态SOC为输出, 搭建符合HPPC工况实验的数据集具体化深度网络模型, 对于具体化深度网络模型则具有3个神经网络输入元, 并且对模糊化深度前馈网络层数与节点数进行数值具体化.

|
图 1 深度前馈神经网络构架 |
首先, 进行BP神经网络隐藏层节点数以及层数的选取. 对于网络隐藏层节点数以及层数的选取都是基于深度前馈网络总体全连接式模糊化架构的条件下进行的.
关于BP神经网络隐藏层节点数问题的讨论有以下几个方法:
1)张清良等[4]学者指出对于神经网络隐藏层节点数、输入节点、输出节点与分类数的关系为:
| ${N_{\rm hid}} = \frac{{{N_{\rm in}} + \max \left\{ {{N_{\rm out}},{N_c}} \right\}}}{2}$ | (1) |
式中,
2) Nielsen[5]在1987年提出了Kolmogorov定理, 给定任一连续函数:
| $f:{\left[ {0,1} \right]^n} \to {R^m}$ | (2) |
式中, f可以精准地用一个三层前向神经网络实现, 隐藏层的节点数与输入层节点数之间的关系为:
| $S = 2n + 1$ | (3) |
式中,n为输入层节点数; S为隐藏层节点数.
3)隐含层节点数设计的经验公式[6]:
| $l = \sqrt {m + n} + d$ | (4) |
式中,n为输入层节点数;m为输出层节点数;d为
针对Dense全连接层为主体自主构建的非线性深度前馈网络以及HPPC工况所采取的40万条数据量, 因此BP神经网络节点数以及网络层数的设计至关重要. 相比于式(1)与式(3)网络节点数选取方法由于经验式(4)计算得到的节点数最能够使收敛速度以及网络精度提升, 所以采用经验式(4)叠加网络层数以及网络节点数的方法来选取最佳的网络结构模型.
输入层节点数n为3, 输出层节点数m为1, 所以对于不同层隐含层节点数取值范围在3~13. 分别取隐含层从1~5叠加, 每层隐含层节点数分别取自3~13, 进行神经网络层的训练, 每次训练60轮, 得到不同层数隐含层的MAE值与Loss值如表1.
| 表 1 基于Adam、Log-cosh不同层数与节点数对比 |
表1所示再设计BP深度前馈网络时, 依据经验式(4), 采用叠加网络层数以及网络节点数的方法可以发现在隐藏层数为3层, 隐藏节点数为11-9-12时所取得的模型效果最好, MAE值为0.0309, Loss值为0.0009. 因此在接下来的优化实验中, 采取此种深度网络模型来进行后续实验操作.
2 深度前馈网络模型优化 2.1 优化器的选取优化器是用来计算更新影响模型训练和输出的权重系数矩阵W与偏倚向量b, 通过优化损失函数, 减小loss值, 提升模型的准确度.
对于自适应学习率优化算法则有AdaGrad、RMSProp、Adam、Nadam等.
在上世纪50年代提出的SGD[7]随机梯度下降算法梯度下降速度快, 但因为参数更新频繁, 会造成损失函数严重震荡, 不易收敛.
2011年提出的AdaGrad算法[8], 在学习率的变化化过程中进行了调整, 对于具有不同偏导参数学习率下降效果不同.
2012年提出的RMSProp算法[9]修改AdaGrad算法在非凸设定效果下更好, 改变梯度积累为指数加权的移动平均.
2014年提出的Adam算法[10], 动量直接并入了梯度一节据估计, 对于超参数有很好的鲁棒性.
Nadam算法[11], 在Adam基础上加入NAG思想, 对学习率有了更强的约束, 同时对梯度的更新也有更直接的影响. 它的具体更新如下:
| $\theta = \theta {\rm{ - }}{{{H}}^{{\rm{ - 1}}}}g$ | (5) |
式中,
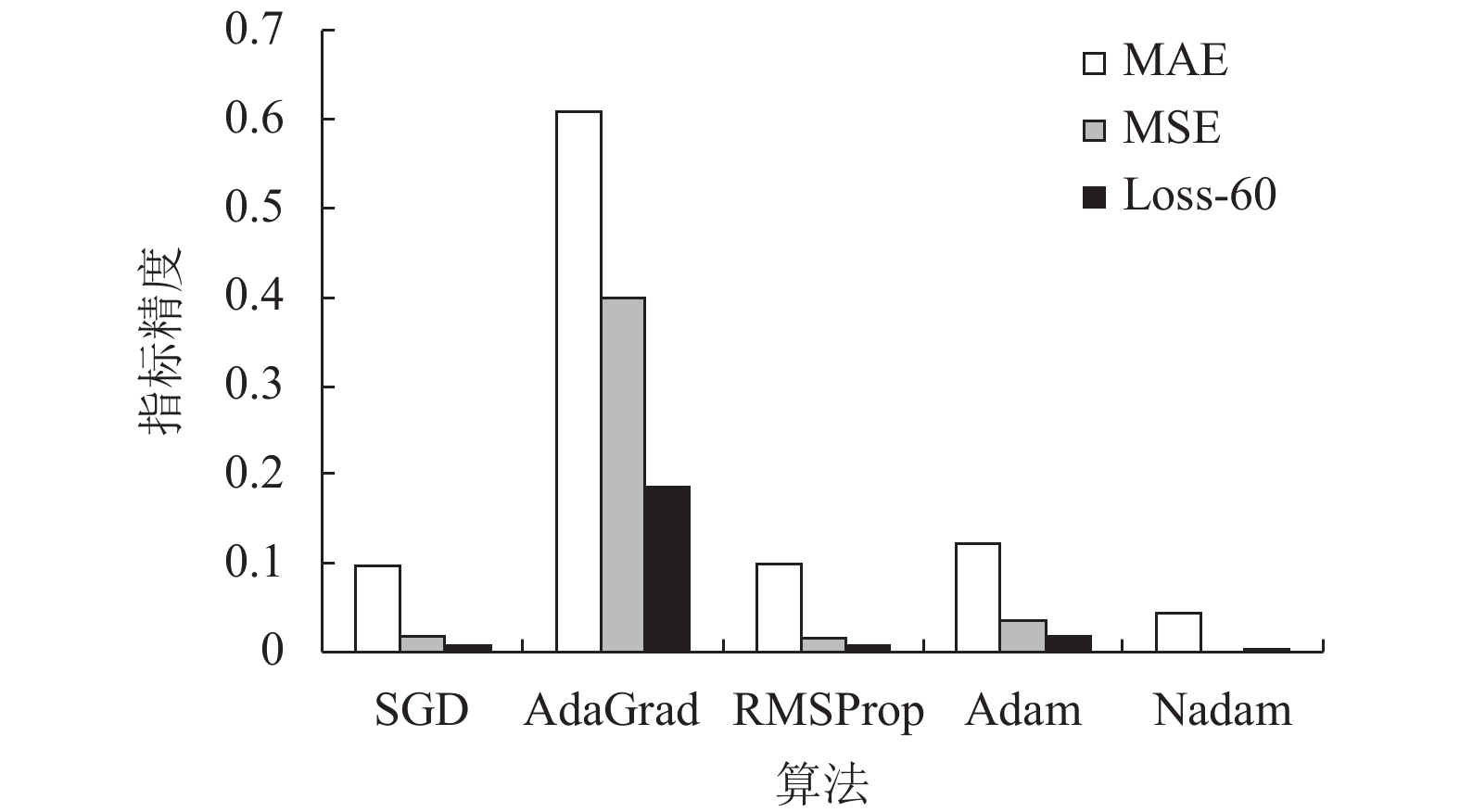
下面将对5种优化器应用在模型效果最好的8层隐藏模型中, 进行对比选取最优优化器进行实验. 图2为5种优化器对比.
|
图 2 基于Log-cosh各类优化器对比 |
由图2可知, 在选定的神经网络框架下, 以Nadam作为优化器, 使得学习率有了更强的约束, 作为Nesterov accelerated gradient与Adam的结合算法, 在训练中达到的效果更优. 并且相对于SGD, AdaGrad、RMSProp、Adam这4种优化器, Nadam优化器所达到的MAE, MSE与损失值都为最小值, MAE为0.0524, MSE为0.0042, Loss为0.0125, 因此选取Nadam优化器作为模型优化器. 这是基于Log-cosh损失函数的优化效果, 为了进一步提升整个训练效果, 将对损失函数进行优化.
2.2 损失函数的优化选择在神经网络中, 损失函数是要优化的目标, 是用来评价网络模型预测值
1) MSE是预测值与真实值之间的欧氏距离值, 这种方法计算简单, 是一种很好的相似形度量标准.
2) MAE就是直接计算出显著性图谱与真值Ground-truth之间的平均绝对误差, 是对数据的绝对误差求平均.
3) Huber损失(平滑平均绝对误差)[12]结合MSE, MAE的优点, 一阶可导当损失很小时采用平方损失, 当损失很大时采用绝对损失, 他会由于梯度的逐渐减小落在最小值的附近, 对于异常点的鲁棒性更加.
4) Log-cosh损失[13]是回归任务中另一个函数, 他所预测的是误差的双曲线余弦的对数. 他的损失函数定义公式如下:
| $L\left( {Y,\hat Y} \right) = \sum\limits_{i = 1}^N {\log \left( {\cosh \left( {\hat {y_i} - {y_i}} \right)} \right)} $ | (6) |
式中,
下面将对4种损失函数应用在模型效果最好的3层隐藏模型中, 使用测试数据进行评估对比选取最优损失函数进行实验. 表2为4种损失函数对比.
4种损失函数的Loss随迭代次数Epoch变化曲线如图3.
| 表 2 基于Log-cosh各类优化器对比 |

|
图 3 4种损失函数的Loss变化曲线 |
由表2与图3可以看出将Log-cosh作为损失函数进行模型的优化所得到的Loss最小, 损失曲线也更为平滑连接.
2.3 过拟合解决措施对于HPPC低温工况下测得的数据, 将PAU停止工作阶段数据进行剔除, 将CHA充电阶段与DCH放电阶段数据按照6:1的比例划分为训练集与测试集.
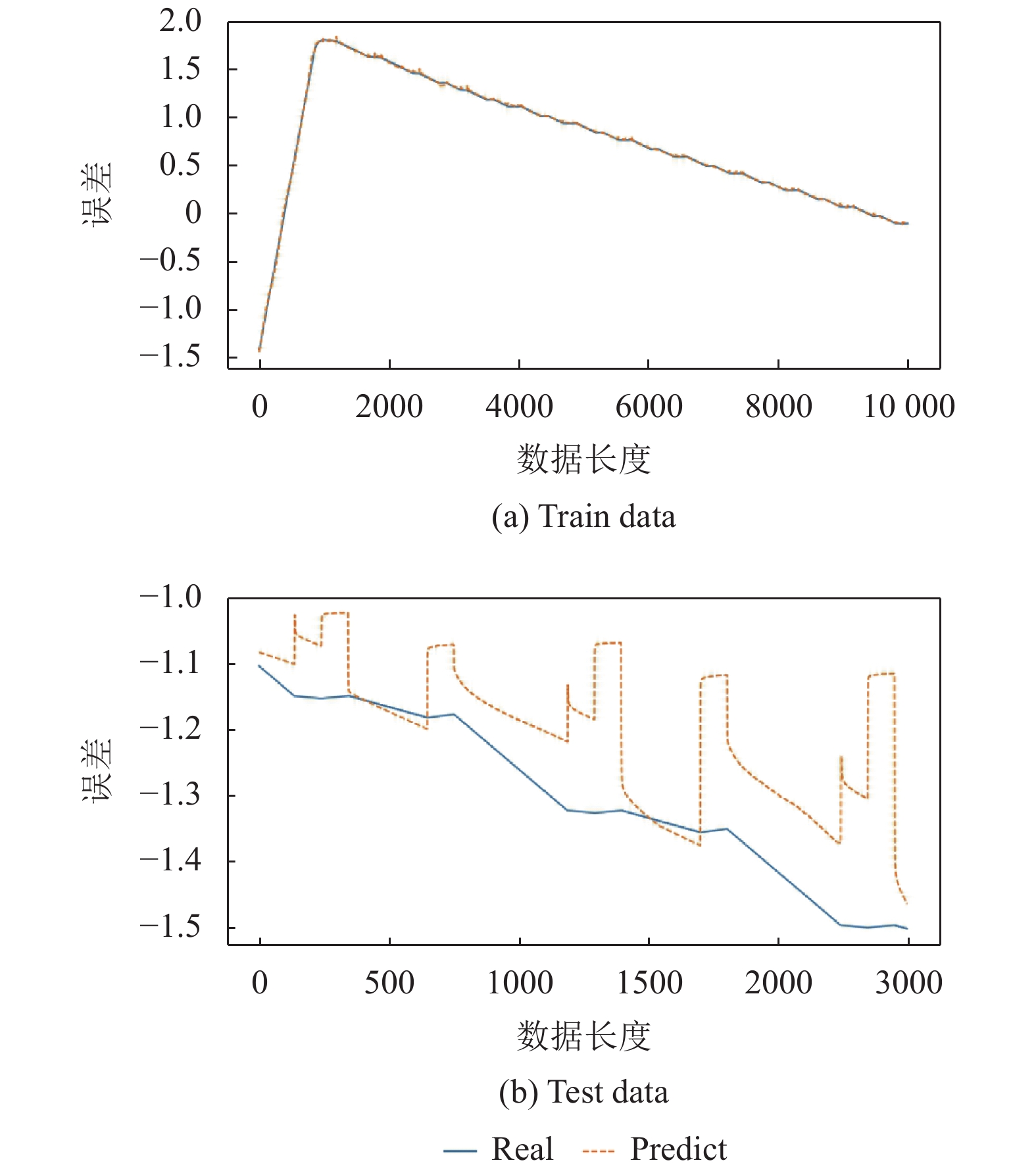
过拟合的表现为, 在训练数据上表现较好, 在测试集中泛化能力较差, 图4为没有解决过拟合问题的训练集与测试集的误差表现.
过拟合措施有L-M法, 提前停止法, 正则化等[14].
由图4可以看出, 训练集误差可以忽略不计, 但是测试集误差出现悬崖式突变值. 为了减小测试误差, 采用正则化方法进行权重衰减.
图5为采用正则化措施后解决过拟合问题的训练集与测试集的误差表现.
可以看出正则化之后的训练误差与测试误差都保持在合理范围之内.
3 深度神经网络数学模型深度神经网络模型的构建需要一定的数学模型作为基础. 首先对于模型进行初始化连接权值与节点阈值, 再进行数据样本的输入. 进行前向传播, 通过模型进行隐含层节点输出计算与输出层输出计算, 计算隐含层与输出层的误差, 进行反向传播, 更新连接权值与节点阈值, 在模型中使用L1正则化与L2正则化联合解决过拟合问题, 进行60次迭代训练.
整个神经网络深度模型内部流程如图6.
|
图 4 无过拟合训练测试误差曲线 |

|
图 5 过拟合训练测试误差曲线 |
对于模型数学过程推导如下.
输入样本有电流I和电压U两个输入特征, 一个SOC输出特征, 数据集整个输入样本训练集表现形式为

|
图 6 深度模型流程图 |
1)正向传播过程.
| ${Z^l} = {W^{lT}}{X^{l - 1}} + {b^l}$ | (7) |
式中,
对于正向传播过程的输入有两种形式, 第一层隐藏层的输入为U和I. 对于其他层的隐藏层的输入如下:
| ${A^h} = \sigma \left( {{Z^h}} \right) = \hat Y$ | (8) |
式中,
下面计算所要优化的成本函数. 采取的损失函数为Log-cosh. 损失函数的表达式为式(6)所示. 成本函数如下式所示:
| $J\left( {w,b} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {L(Y,\hat Y)} + \frac{\alpha }{2}\left\| w \right\|_2^2 + \beta {\left\| w \right\|_1}$ | (9) |
式中,
2)反向传播过程.
在反向传播过程中使用Nadam优化算法,
更新
| $w = w - \eta * \frac{{\overline {{m_{t1}}} }}{{\sqrt {S_{dw}^c} + \varepsilon }}$ | (10) |
| $b = b - \eta * \frac{{\overline {{m_{t2}}} }}{{\sqrt {S_{db}^c} + \varepsilon }}$ | (11) |
| 表 3 符号说明表 |
4 实验与结果分析
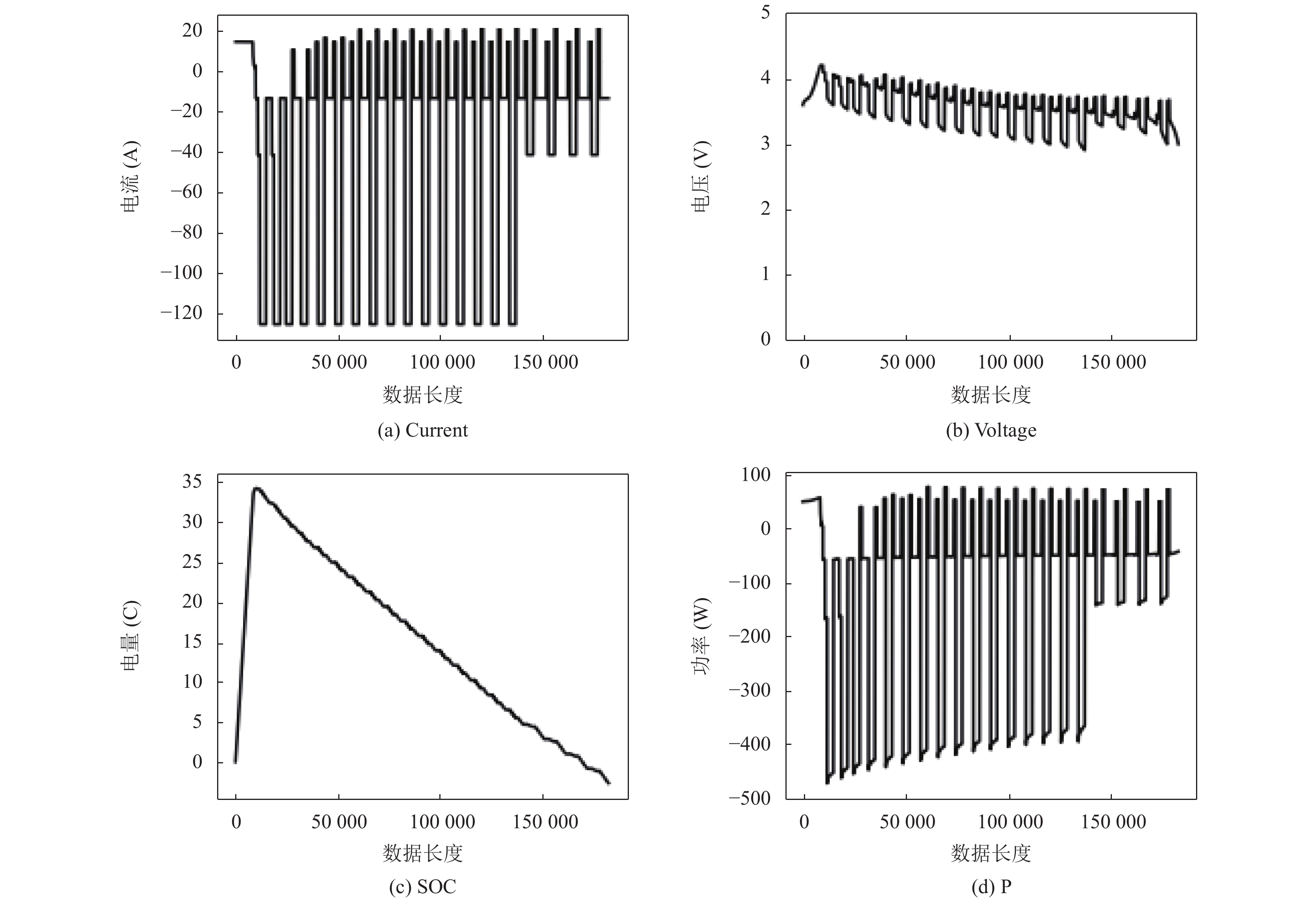
实验采用HPPC测试方法, 在0度低温下通过对充放电电压U, 充放电电流I, 充放电功率P进行监测, 通过深度神经网络模型进行预测得到实时SOC. 实验采用的锂电池电池容量为42 Ah. 实验测得415287组测试数据, 对于数据需要进行数据的预处理, 首先对数据进行筛选, 将停止工作的电流电压数据进行剔除, 只保留充电与放电的数据, 再进行缺失值处理, 缺失值用缺失值前后的数据平均进行填充, 再将数据输入模型之前最后进行数据标准化的处理, 以减小数据的分散度. 在经过数据预处理后得到高质量数据样本, 对于处理后的实验数据进行划分设置, 由于是时间序列形式的数据, 因此将前15000行数据作为训练数据, 将后2500行数据作为测试数据. 使用模型对数据进行训练和预测. 图7为实验所测得各个监测参数随时间变化的曲线图.
由图中可以看出电流电压功率存在负值与的情况, 表明在负值时放电, 在正值时电池处于充电状态.
实验进行SOC训练预测采用的处理器为Intel(R)Core(TM)i7-8750H-CPU@2.20 GHz-2.21 GHz. 实验进行5次交叉验证, SOC预测得出误差如表4, 表4中的平均绝对误差为MAE值.
|
图 7 参数变化图 |
由表4可以看出SOC预测值与真实值的平均误差基本维持在0.04左右. 模型训练运行时间为19.9秒, 对于60次迭代来说, 平均每次迭代花费0.33秒, 所运行的时间较短, 因此采用基于SGD扩展的使用动量和自适应学习率来加快收敛速度Nadam优化算法以及Log-cosh损失函数优化完善的模型, 在进行正则化处理之后, 可以大大提升SOC预测精度.
由HPPC试验所得到的实验数据, 设计拥有1层输入层, 3层隐藏层, 1层输出层的深度前馈神经网络, 采用Log-cosh损失函数与Nadam优化器进行模型精度的提升, 使用正则化进行过拟合处理. 得到的损失值为0.0125, 相对于其他SOC估计算法, 精确性大大提升. 表5为BP神经网络, RBF神经网络, 线性回归, 支持向量机四种算法MAE平均绝对误差对比表.
| 表 4 误差表 |
| 表 5 算法对比表 |
图8为BP神经网络, RBF神经网络, 线性回归, 支持向量机4种算法训练运行时间对比图. 可以看出所设计的BP深度前馈神经网络在训练精度上远远超过其他算法, 每轮所需时间也仅只有0.33 s.

|
图 8 时间对比图 |
5 结论
由在HPPC工况下进行实验得到的实验数据, 参考以往的神经网络节点设计经验, 运用数学规划方法对不同节点数以及隐藏层数的深度前馈神经网络架构进行设计以及性能分析, 选择了隐藏层数为3层, 隐藏节点数为11-9-12时的模型, 完整的网络模型结构为3-11-9-12-1. 同时为了加强对学习率的约束, 以及加强对梯度的更新的影响, 采用了基于SGD扩展的使用NAG动量和自适应学习率来加快收敛速度的Nadam优化算法. 为了提升SOC预测的精确度, 采用了Log-cosh作为模型的损失函数. 为了提升模型在测试时的精度, 通过正则化措施解决模型的过拟合问题. 经实验测试实现了在不同电压电流条件下所预测的SOC误差在0.04左右, 损失函数曲线过度更加平滑, 损失值更小.
模型在强有力的数学理论支撑下, 在经过前向传播与后向传播获得结果最优损失函数参数, 达到理想的模型预测精度. 在与其他模型算法进行精度与运行时间的对比上, 本模型能够较为精准的为在充放电状态下的电动汽车SOC提供可靠的实时容量预测, 具有较大的参考价值.
| [1] |
胡晓松, 唐小林. 电动车辆锂离子动力电池建模方法综述. 机械工程学报, 2017, 53(16): 20-31. |
| [2] |
尤晓东, 苏崇宇, 汪毓铎. BP神经网络算法改进综述. 民营科技, 2018(4): 146-147. |
| [3] |
王晨, 王琪, 张萌. 粒子群优化神经网络的动力电池SOC估算研究. 单片机与嵌入式系统应用, 2020, 20(6): 20-23, 29. |
| [4] |
张清浪, 李先明. 一种确定神经网络隐层节点数的新方法. 吉首大学学报(自然科学版), 2002, 23(1): 89-91. |
| [5] |
Nielsen RH. Kolmogorov’s mapping neural network existence theorem. Proceedings of the IEEE 1st International Conference on Neural Networks. San Diego, CA, USA. 1987. 11–13.
|
| [6] |
韩力群. 人工神经网络理论、设计及应用. 北京: 化学工业出版社, 2002.
|
| [7] |
Ruder S. An overview of gradient descent optimization algorithms. arXiv: 1609.04747, 2016.
|
| [8] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. The Journal of Machine Learning Research, 2011, 12: 257-269. |
| [9] |
Tieleman T, Hinton G. Lecture6.5—RMSprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural network for Machine Learning, 2012, 4(2): 26–31.
|
| [10] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv: 1412.6980, 2014.
|
| [11] |
Dozat T. Incorporating nesterov momentum into adam. Proceedings of the 4th International Conference on Learning Representations. San Juan, Puerto Rico. 2016.
|
| [12] |
李德才. 基于多元时间序列的关联分析及预测方法研究[博士学位论文]. 大连: 大连理工大学, 2012.
|
| [13] |
李俭川, 秦国军, 温熙森, 等. 神经网络学习算法的过拟合问题及解决方法. 振动、测试与诊断, 2002, 22(4): 260-264. DOI:10.3969/j.issn.1004-6801.2002.04.003 |
| [14] |
张芳芳, 李楠. 基于独立成分分析的fMRI数据分类. 计算机应用与软件, 2019, 36(11): 107-111. DOI:10.3969/j.issn.1000-386x.2019.11.018 |
 2021, Vol. 30
2021, Vol. 30



