鉴于传统无线网络固有的安全威胁, 要保障网络的正常运行, 安全通信是至关重要的基础和前提. 现有的机制通常是采用加密以及认证技术来保证安全. 传统的密钥建立机制都是基于共享密钥或公共密钥^[1], 但是这些方法通常要涉及到密钥的管理、分发、更新以及维护, 当网络内的用户节点个数不断增加时, 密钥的管理难度也会极大增加. 为了解决以上问题, 近年来, 利用物理层安全来增强无线网络安全的研究受到了广泛的关注. 物理层密钥生成机制是从无线信道特征中提取密钥, 通信双方可以在不借助于公钥基础设施或者是共享密钥的情况下进行密钥协商.

在物理层密钥提取中所利用的信道特征可以是接收信号强度 (Received Signal Strength, RSS)^[2-4], 信道状态信息(Channel State Information, CSI)^[5,6], 或信道相位^[7,8]. 因为RSS在无线信道中更容易被提取, 所以基于RSS密钥生成机制的研究更为广泛. 虽然基于物理层无线信道特征的密钥生成方案在两个用户之间易于实现, 但在实际应用中, 由于一对用户节点之间提取的信道测量值无法安全有效地传递到其他用户, 换句话说, 在多个用户节点上累积信道测量值用于生成组密钥仍是一个很大的挑战. Liu等^[9]首先针对星型拓扑结构, 提出了一个高效的组密钥生成方案. 然后进一步考虑到网络中两个用户节点之间不一定在彼此的通信范围, 节点间的通信需要依靠其他节点进行转发, 因此Liu等从逻辑上构造了一种链式拓扑结构, 并针对链式拓扑结构利用差分思想提取组密钥. 文献[10]对文献[9]做了补充, 并从理论上分析了方案可达的组密钥率. Thai等^[11]将网络中的一个节点通过一条重要信道与其他节点相互链接, 每个节点广播具有优化系数的不同信道特征值的加权组合, 优化的系数可以帮助重新平衡来自不同节点的接收信号强度以增强组密钥生成方案的性能. Tunaru等^[12]研究了脉冲无线电-超宽带多径信道的密钥协议, 提出一种新的组密钥生成方案, 利用全网状拓扑中所有可用物理链路, 使接收信号节点可以访问与其非相邻链路相对应的不可观察信道, 同时还减少了网络流量, 但是该方案没有分析广播时可能泄漏给窃听者的信息量. Xu等^[13]针对不同的无线拓扑, 提出一种新的低复杂度密钥生成策略, 该策略将成熟的点对点密钥生成技术与多段方案进行巧妙的组合. 首先, 通过近似算法将非凸时间分配最大-最小问题重新表述为一系列几何规划, 然后提出一种迭代算法在训练阶段解决时间分配问题, 最大程度提高了组密钥率. 章红艳等^[14]利用超立方体对无线传感器网络节点进行编码的思路, 实现了节点对密钥的建立, 使无线传感器网络具有较强的抗毁性.

本文提出了一种适用于网状拓扑的无线网络中基于三节点的组密钥生成方案.

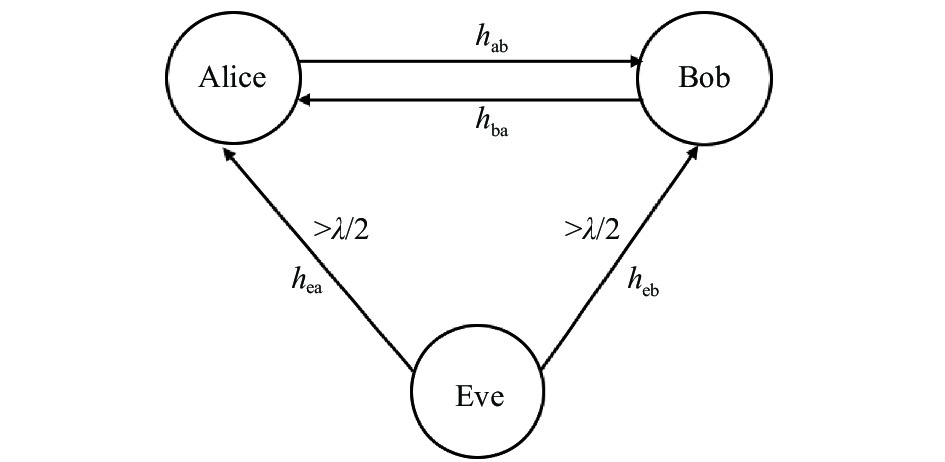
1 系统模型

图1代表的是一个密钥生成模型, 其中Alice、Bob代表合法通信双方, 而Eve表示窃听者. ${h_{\rm ab}}$ , ${h_{\rm ba}}$ , ${h_{\rm ea}}$ , ${h_{\rm eb}}$ 分别表示各自信道的信道增益, λ表示波长, 也就是说Eve距离合法通信双方Alice和Bob至少半波长远.

我们假设Eve可以窃听通信双方, 即Alice和Bob之间的通信信号. 由于无线信道采用的是半双工通信方式, 用户在进行通信时不能同时发送和接收消息, 因此Bob必须在接收到Alice发送来的消息后才能返回一个消息给Alice, 反之亦然. 我们用表示Alice和Bob之间无线信道的信道增益, 则通信双方接收信号可以表示为:

${r_{\rm{a}}}({t_{\rm{1}}}) = s({t_1}){h_{\rm ab}}({t_1}) + {n_{\rm{a}}}({t_1})$

(1)

${r_{\rm{b}}}({t_2}) = s({t_2}){h_{\rm ba}}({t_2}) + {n_{\rm{b}}}({t_2})$

(2)

其中, ${r_{\rm{a}}}({t})$ , ${r_{\rm{b}}}({t})$ 分别表示Alice和Bob接收到的信号; $s(t)$ 表示发送的探测信号; ${n_{\rm{a}}}(t)$ , ${n_{\rm{b}}}(t)$ 分别代表Alice和Bob在接收到信号时刻周围的环境噪声. 通过测量Alice和Bob分别得到各自的接收信号, 然后双方利用接收信号可以通过式(3)、式(4)计算各自的信道估计值:

${\hat h_{\rm ab}}({t_1}) = {h_{\rm ab}}({t_1}) + {{\textit{z}}_a}({t_1})$

(3)

${\hat h_{\rm ba}}({t_2}) = {h_{\rm ba}}({t_2}) + {{\textit{z}}_{\rm{b}}}({t_2})$

(4)

其中, $h(t)$ 通过式(1), (2)可以计算得到; ${{\textit{z}}_{\rm{a}}}(t)$ , ${{\textit{z}}_{\rm{b}}}(t)$ 分别代表 ${n_{\rm{a}}}$ , ${n_{\rm{b}}}$ 经过函数处理后的噪声项. 根据式(3)和(4), Alice和Bob分别可以推导出 ${\hat h_{\rm ab}}({t_1})$ 和 ${\hat h_{\rm ba}}({t_2})$ . 事实上, 由于半双工通信导致 ${t_1} \ne {t_2}$ , 再加上周围环境噪声的影响, 所以 ${\hat h_{\rm ab}}({t_1})$ 和 ${\hat h_{\rm ba}}({t_2})$ 并不完全相等. 但是根据无线信道短时互易性^[15], 只要 ${t_1}$ 和 ${t_2}$ 之间的差小于相干时间, 则 ${\hat h_{\rm ab}}({t_1})$ 和 ${\hat h_{\rm ba}}({t_2})$ 之间是高度相关的, 即如果 $|{t_1} - {t_2}| < \tau $ , 则 ${\hat h_{\rm ab}}({t_1}) \approx {\hat h_{\rm ba}}({t_2})$ .

如图2所示, 考虑网络中3个用户节点的情况, 其中节点1和3不在彼此的通信范围内, 这意味着节点1和节点3只能通过节点2进行通信.

我们将通信过程分为4个阶段:

阶段1: 节点2广播信号, 节点1和3收到信号后提取到各自的信道估计值:

$\left\{\begin{split} &{\phi _{1,1}} = {h_{12}}(t)\\ &{\phi _{1,3}} = {h_{23}}(t) \end{split}\right.$

其中, ${\phi _{i,j}}$ 表示节点j在第i阶段结束后提取到的信道估计值.

阶段2: 节点2收到节点1回复的信号, 提取信道的估计值 ${h_{12}}(t)$ , 令 ${\phi _{2,2}} = {h_{12}}(t)$ .

阶段3: 与阶段2相类似, 节点2收到节点3的回复信号并提取信道的估计值 ${h_{23}}(t)$ , 令 ${\phi _{3,2}} = {h_{23}}(t)$ .

阶段4: 经过以上阶段后, 节点2获得 ${h_{12}}(t)$ 和 ${h_{23}}(t)$ . 节点2广播 ${h_{12}}(t) + {h_{23}}(t)$ , 则节点1和节点3根据本地的信息可以分别得到 ${h_{12}}(t) * ({h_{12}}(t) + {h_{23}}(t))$ 和 ${h_{23}}(t) * $ $ ({h_{12}}(t) + {h_{23}}(t))$ , 最终两个节点可以分别得到 ${\phi _{4,1}} = {h_{12}}(t) * $ $ {h_{23}}(t)$ 和 ${\phi _{4,3}} = {h_{12}}(t) * {h_{23}}(t)$ .

同时, 由于节点2同时具有 ${h_{12}}(t)$ 和 ${h_{23}}(t)$ , 所以它也可以计算得到 ${h_{12}}(t) * {h_{23}}(t)$ .

2 组密钥生成协议

本文的组密钥生成协议包含4个阶段:

(1)初始化阶段. 在此阶段, 受信任的系统授权机构将为网络中的用户节点进行分组, 组内节点从逻辑上形成一个环路. 同时, 受信任的系统授权机构进行一 次初始化的操作, 还将生成密钥建立协议中所需的一些参数.

(2)密钥提取阶段. 在此阶段用户利用物理层无线信道特征提取短密钥.

(3)信息交换阶段. 在此阶段用户节点广播一些信息, 并记录所交换的信息.

(4)组密钥建立阶段. 在此阶段, 每个用户节点都对自己的邻居节点进行身份验证, 验证成功后这些节点可以建立一个组密钥.

2.1 初始化

在此阶段, 受信任的系统授权机构将为网络中的用户节点进行分组, 组内节点从逻辑上形成一个环路, 并为逻辑环上每个节点分配一个身份标识 $I{D_i}$ . 我们用 $\prod $ 表示组内所有用户的集合, 并假设每个用户节点 $v \in \prod $ . 在提取密钥之前, 组内n个合法用户形成一个逻辑环, 记为 ${v_1},{v_2},\cdots,{v_n}$ . 由于所有用户在逻辑上形成一个环路, 因此 ${v_{n + 1}} = {v_1}$ , ${v_0} = {v_n}$ .

数字签名作为保障网络信息安全的手段之一, 在包括身份认证、数据完整性验证以及不可否认性等信息安全领域发挥着重要的作用. 因本文考虑的网络环境为无线网络, 故节点的能耗和存储代价是需要考虑在内的. Schnorr签名^[16]因以其计算量小和速度快著称, 且安全性基于某些离散对数问题的难处理性, 故被广泛应用到网络安全等领域. 因为它所具备的显著优点, 所以本文选择Schnorr签名技术对交换的信息进行签名, 以防止数据被篡改.

2.2 密钥提取

在此阶段, 用户在物理层提取密钥. 环中每个用户都有两个邻居节点, 分别构成节点对 $ < {v_{i - 1}},{v_i} > , < {v_i},{v_{i + 1}} > $ , $i = 1,2,\cdots,n$ , 其中两个邻居节点之间的距离要小于 $\lambda /2$ . 根据系统模型, 每个节点分别与其相邻节点利用物理层无线信道特征提取短密钥, 则每个用户都会获得 ${k_{i - 1,i}}$ 和 ${k_{i,i + 1}}$ , 如图3所示.

然后, 将环上相邻的3个节点设为一小分组, 生成3个节点之间的共享密钥. 如图4所示, 我们以节点 ${v_1}$ , ${v_2}$ 和 ${v_3}$ 为例, 3个节点根据系统模型中所描述的方式反复发送探测信号后收集到足够的信道估计值 ${h_{12}}(t) * $ $ {h_{23}}(t)$ , 利用文献[4]所提的密钥生成方案将提取到的信道估计值进行量化编码以及协商之后生成3个节点之间的密钥. 以此类推, 最后逻辑环上的每个节点都分别得到如图4所示的3个共享密钥, 其中 ${k_i}$ 表示以第i个节点为中心所生成的共享密钥.

2.3 信息交换

用户 ${v_i}$ 计算:

$\left\{\begin{array}{l} {X_i} = H({k_{i - 1,i}}) \oplus H({k_{i,i + 1}}) \\ V_i^{i - 1} = {k_{i - 1}}(H({k_{i - 1,i}}) \oplus I{D_i}) \\ V_i^{i + 1} = {k_{i + 1}}(H({k_{i + 1,i}}) \oplus I{D_i}) \\ \end{array} \right.$

然后, 节点 ${v_i}$ 在公共控制信道上广播消息: $m_i = $ $ < {v_i},{v_{i - 1}},V_i^{i - 1};{v_i},{v_{i + 1}},V_i^{i + 1};X_i >$ , 经过信息交换后, 每个节点都会获得所有的广播消息 ${m_1},{m_2},\cdots,{m_n}$ .

2.4 组密钥建立

接收到所有广播消息之后, 每个节点 ${v_i}$ 要完成两件事:

(1)验证邻居节点 ${v_{i - 1}}$ 和 ${v_{i + 1}}$ . 首先, 节点 ${v_i}$ 需要验证消息 ${m_{i - 1}}$ 和 ${m_{i + 1}}$ 是否来自邻居节点, 然后 ${v_i}$ 利用本地保存的密钥 ${k_i}$ 解密 $V_i^{i - 1}$ 和 $V_i^{i + 1}$ . 以节点 ${v_2}$ 为例, ${v_2}$ 通过验证消息 ${m_1}$ 和 ${m_3}$ , 分别可以提取到信息: $V_1^2 = {k_2}(H({k_{1,2}}) \oplus I{D_1})$ 和 $V_3^2 = {k_2}(H({k_{2,3}}) \oplus I{D_3})$ , 然后通过本地保存的密钥 ${k_2}$ 解密两个信息, 并将本地计算得到的 $H({k_{1,2}}) \oplus I{D_1}, $ $ H({k_{2,3}}) \oplus I{D_3}$ 与解密后的信息进行对比, 一致则认为验证成功.

(2)检查 ${X_1} \oplus {X_2} \oplus \cdots \oplus {X_n}$ 是否等于0. 以上两个验证只要有一个不通过, 则组密钥建立协议终止.

(3)计算组内所有密钥. 节点 ${v_i}$ 可以计算密钥, 此时分为3种情况:

① 当 $j = 0$ 时, ${K_i} = H({k_{i,i + 1}})$ ;

② 当 $j = 1,2,\cdots,n - 2$ 时, ${K_{(i + j)od n}} = H({k_{i,i + 1}})\; \oplus $ $ {X_{(i + 1)od n}} \oplus \cdots \oplus {X_{(i + j)od n}}$ ;

③ 当 $(i + j)od n = 0$ 时, ${K_n} = {K_0} = H({k_{i,i + 1}}) \;\oplus $ $ {X_{i + 1}} \oplus \cdots \oplus {X_n}$ .

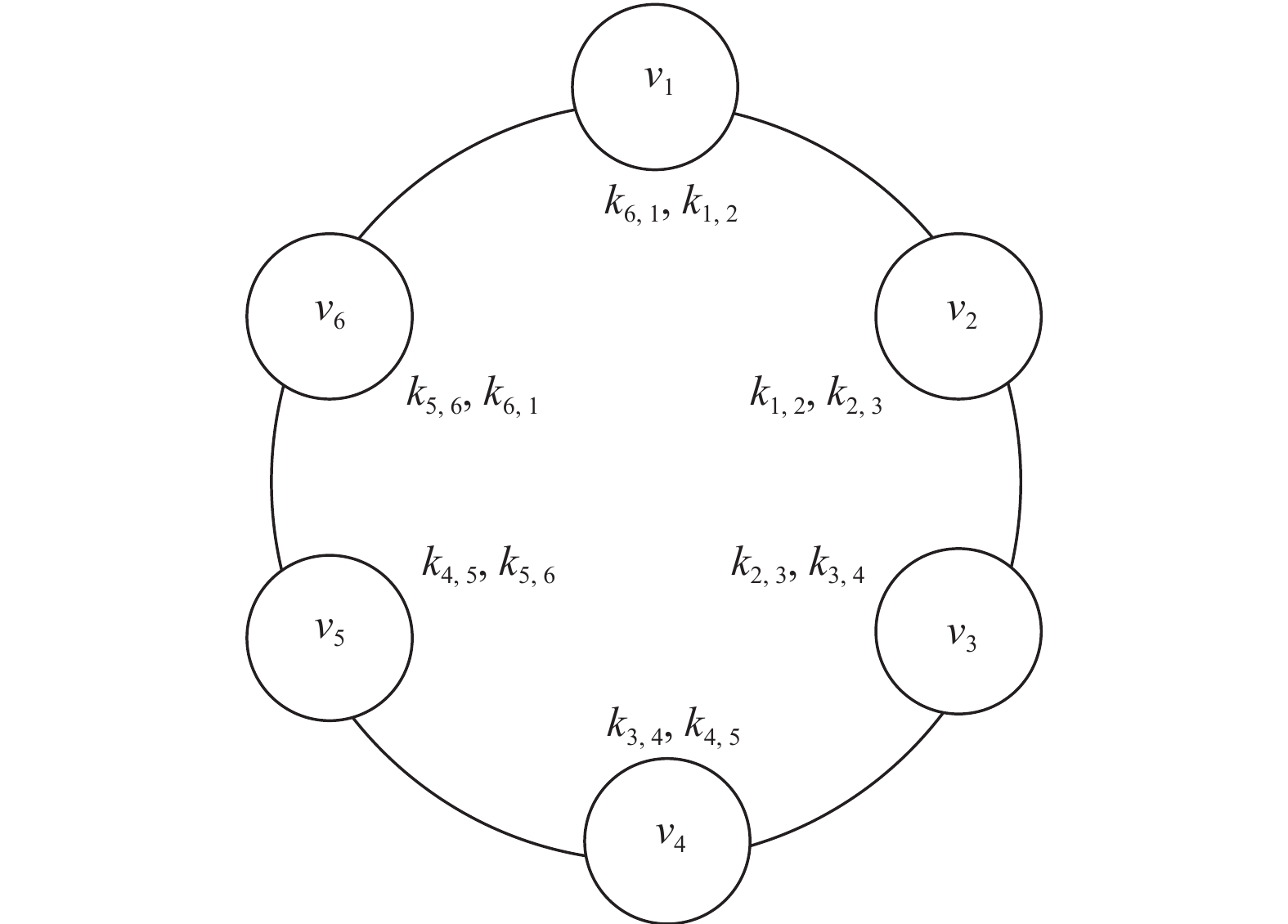
为了方便理解, 我们以组内节点个数为6, 节点 ${v_2}$ 为例, ${v_2}$ 可计算得到:

${K_2} = H({k_{2,3}})$

${K_3} = {k_{(2 + 1)od 6}} = H({k_{2,3}}) \oplus {X_3}$

${K_4} = {k_{(2 + 2)od 6}} = H({k_{2,3}}) \oplus {X_3} \oplus {X_4}$

${K_5} = {k_{(2 + 3)od 6}} = H({k_{2,3}}) \oplus {X_3} \oplus {X_4} \oplus {X_5}$

$ {K_6} = {k_0} = {k_{(2 + 4)}}_{od 6} =H({k_{2,3}}) \oplus {X_3} \oplus {X_4} \oplus {X_5} \oplus {X_6} \\ $

$ {K_1} ={k_{(2 + 5)}}_{od 6} =H({k_{2,3}}) \oplus {X_3} \oplus {X_4} \oplus {X_5} \oplus {X_6} \oplus {X_1} \\ $

(4)计算最终的组密钥. 经过以上步骤后, 逻辑环上的每个节点都获得组内所有的密钥, 然后节点 ${v_i}$ 计算最终的组密钥 ${K}_{g}={K}_{1}\cdot{K}_{2}\cdot\;\cdots\;\cdot{K}_{n}$ . 最终, 组内用户成功建立共享组密钥.

3 性能分析 3.1 可实现的组密钥率

由上述组密钥率生成方案可知, 最终生成的组密钥与逻辑环路上两两相邻的节点的共享对密钥有关, 所以可实现的最大组密钥率与相邻两个节点之间的信道观察互信息^[17]:

$ \begin{split} {R_{i,i + 1}} =& I\left( {\hat Y_{i + 1,i}^i,\hat Y_{i,i + i}^{i + 1}} \right)\\ =& {\log _2}\left( {1 + \dfrac{{{{\left( {\sigma _Y^2} \right)}^2}}}{{\sigma _Y^2\dfrac{{\left( {\sigma _{i + 1}^2 + \sigma _i^2} \right)}}{2} + \dfrac{{\sigma _{i + 1}^2\sigma _i^2}}{4}}}} \right) \end{split} $

(5)

${R_{i,i + 1}}$ 表示节点 $i$ 与 $i + 1$ 之间的信道观察互信息; $\sigma _Y^2$ 表示信道观察信息的实际信道增益方差; $\sigma _i^2$ , $\sigma _{i + 1}^2$ 分别表示节点 $i$ 和 $i + 1$ 的噪声方差, 我们假设噪声对于网络中所有的节点来说都是独立同分布, 并服从均值为0, 方差为 ${\sigma ^2}$ 的高斯分布, 则 ${\sigma ^2} = \sigma _i^2 = \sigma _{i + 1}^2$ . 将 ${\gamma _m} = $ $ {{2\sigma _Y^2} / {{\sigma ^2}}}$ ^[15], 代入式(5)可知本方案的组密钥率为:

$R = {\log _2}\left( {1 + \frac{{\gamma _m^2}}{{2{\gamma _m} + 1}}} \right)$

(6)

3.2 安全性分析

在密钥提取阶段, 合法通信方根据收集到的信道增益在本地生成密钥. 根据通信原理^[18]可知, 当攻击者距离通信方超过半波长远时, 攻击者无法根据观察到的信道增益推测出合法通信方所生成的密钥, 所以该阶段生成的密钥其安全性是可靠的.

在密钥交换阶段, 我们首先Schnorr签名技术对交换的信息进行签名, 以防止数据被篡改. 其次, 组内节点在公共信道上传递经过处理后的消息. 该阶段存在以下几种情况:

(1)消息 ${m_i}$ 遭到篡改: 当节点 ${v_i}$ 收到消息 ${m_i}$ 后, 首先利用保存的密钥解密该消息, 然后将本地计算得到的信息与解密后的信息进行对比, 如果二者不一致说明消息 ${m_i}$ 已被篡改, 密钥生成协议终止, 从而保证了本方案的安全性.

(2)当 ${X_1}, {X_2}, \cdots, {X_n}$ 遭到篡改或在传输过程中数据发生错误, 我们的方案通过验证 ${X_1} \oplus {X_2} \oplus \cdots \oplus {X_n}$ 是否等于0, 可以知道数据是否有误. ${X_1} \oplus {X_2} \oplus \cdots \oplus {X_n} = 0$ 时, 说明数据无误, 可以继续进行下一阶段. 相反, 若 ${X_1} \oplus {X_2} \oplus \cdots \oplus {X_n} \ne 0$ , 则说明其中某一个或多个数据发生错误, 应当终止密钥生成, 这同样也保证了本方案的可靠性和安全性.

(3)假设攻击者收集到公共信道上合法通信方所传递的所有消息, 由于在密钥提取阶段攻击者无法获取合法用户本地生成的密钥, 因此不能根据收集到的信息来计算得到最终的组密钥, 因此本文的组密钥生成方案是安全的.

3.3 方案对比

本文通过Matlab仿真模拟无线环境, 采用瑞利信道模型模拟无线信道^[19], 设多普勒频移 ${{{f}}_{{d}}} = 10\;{\rm{Hz}}$ , 采样速率为 ${{{f}}_g} = 40\;{\rm{Hz}}$ , 载波信号频率为2.4 GHz, 并为组内每个节点端加入噪声^[17], 使信噪比在0 dB~30 dB变化. 实验设备及仿真软件为: MacBook Air (处理器: 1.8 GHz Intel Core i5, 内存: 4 GB, 操作系统: macOS Mojave 10.14.6)、Matlab_R2014b.

组密钥率是影响密钥建立效率的性能指标, 根据式(6)可以看出, 本章所提方案的组密钥率随着信噪比的变化而变化. 由于我们方案的组密钥率只与信噪比有关, 而与组内节点个数无关, 因此我们设置观察不同信噪比下组密钥率的变化. 我们在信噪比0~30 dB之间每隔5 dB分别计算本方案理论上可达的组密钥率在表1不同信噪比参数设置下本方案理论上可达的组密钥率, 具体如表1所示. 同时, 在表1中还给出了与之相对应情况下文献[10]星型拓扑结构和链式拓扑结构下组密钥率, 将其与我们的方案进行对比. 从表1中可以看出, 当信噪比为 ${\gamma _m} = 10\;{\rm{dB}}$ 时, 实现的组密钥率为2.5265 bits/sample. 随着信噪比的增大, 组密钥率也开始呈逐步上升趋势, 当 ${\gamma _m} = {\rm{30\;dB}}$ 时, 可达的组密钥率增加至8.9679 bits/sample. 通过以上分析可知, 本方案的组密钥率与信噪比之间呈正相关, 这是由于高信噪比会降低提取信道估计值时的模糊性, 进一步提高了组密钥的一致性, 从而提高了组密钥率.

同时, 观察表1的任意一列, 例如当 ${\gamma _m} = 20\;{\rm{dB}}$ 时, 本方案的组密钥率为5.6654 bits/sample, 而文献[10]星型拓扑结构以及链式拓扑结构在节点个数为3的情况下组密钥率分别是4.6935 bits/sample, 2.6423 bits/sample. 并且, 随着组内节点个数的增多, 两个方案可达的组密钥率逐渐下降. 我们可以发现, 在信噪比相同的任意情况下, 本方案的组密钥率是远大于文献[10]所提方案的.

此外, 图5表明, 当组内仅有两个用户节点时, 即 $n = 2$ , 本方案的组密钥率与文献[10]在星型拓扑结构下所提方案的组密钥率相等. 这是由于当组内仅有两个节点时, 代表只需在双方节点之间生成对密钥, 这种情况下无需在网络中广播信道信息, 因此窃听者在整个密钥提取过程中很难窃听到额外的任何信息, 这就与本方案的想法相一致, 故两个方案之间的组密钥率相等.

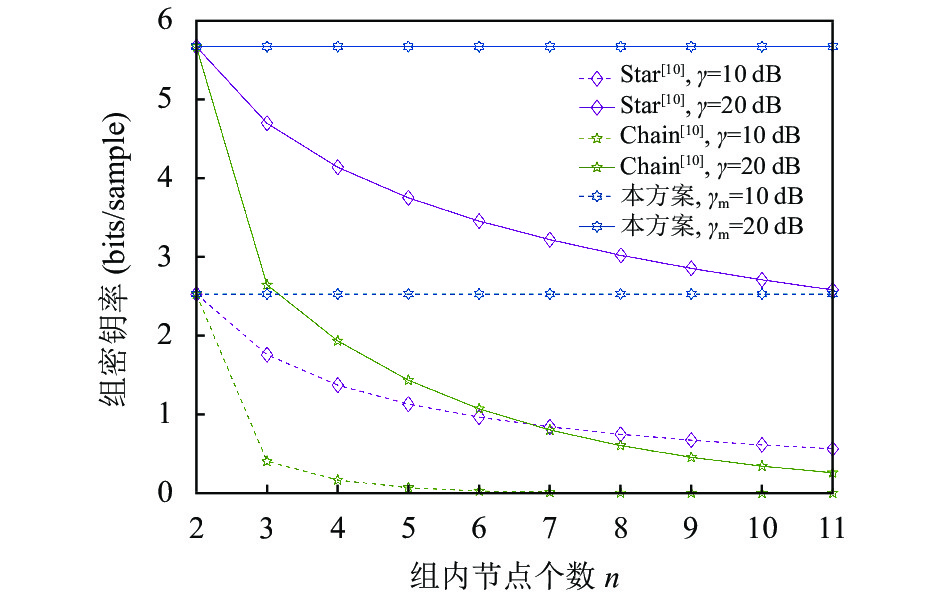
但是, 观察图6可知, 当组内节点个数大于2时, 本方案的组密钥率远远大于文献[10]分别在两种拓扑结构下所提的两种方案. 这是由于文献[10]所提方案中噪声方差随组内节点个数增加呈线性增长, 换句话说, 在通信过程中噪声不断累积最终导致信噪比下降, 从而造成组密钥率降低. 而本文的方案由于最终生成的组密钥与逻辑环路上两两相邻的节点的共享对密钥有关, 噪声变化与组内节点个数无关, 也就是说组密钥率与节点个数之间无关, 因此图6中本方案的组密钥率曲线是平行于 $ x $ 轴. 通常情况下组密钥率与信噪比和组内节点个数有关. 然而, 根据上述分析可知, 本方案的组密钥率只与信噪比有关, 换句话说, 我们方案的密钥生成速率不会随着组内节点个数的增多而下降. 而文献[10]所提方案, 其信道增益在组内各个用户节点之间传递时都会累积噪声, 造成一定的功率损失. 这意味着, 随着网络规模的扩大, 我们方案可以减少由于噪声累积而造成性能的下降, 从整体上来说, 可以减缓组密钥率下降的速度.

4 结论

本文利用物理层无线信道特征提出了一种基于三节点的组密钥生成方案. 该方案首先选择一个受信任的系统授权机构为网络中的用户节点进行分组, 使得组内节点从逻辑上形成一个环路; 然后网络中节点用户利用物理层无线信道特征提取短密钥, 并交换使用Schnorr签名后的信息, 最后, 待每个用户节点接收到所有广播消息之后, 都对自己的邻居节点进行身份验证. 若验证成功, 则为网络中的节点建立一个组密钥. 仿真结果表明, 该方案的组密钥率与信噪比之间呈正相关, 有效提高了网络中的组密钥率, 且组密钥率不随节点个数的增加而降低, 具有很好的无线网络适应性.