随着微博、推特等社交平台成为人们日常生活中信息的主要来源, 在网络中进行评论与交谈信息的语义挖掘和关联信息的研究对于互联网应用(如: 文本分类, 社区发现, 兴趣推荐)来讲是非常有价值的^[1,2], 其中最为基础的是主题模型的研究.

传统主题模型例如PLSA (Probabilistic Latent Semantic Analysis)和LDA (Latent Dirichlet Allocation)被广泛地用来推断文档的潜在主题结构. 在线PLSA模型^[3]在文档流中使用一个固定大小的移动窗口, 以合并新文档同时丢弃旧文档, 从而动态地更新训练模型. LDA^[4]构建了一个三层贝叶斯模型, 每个文档可以看作是主题的多项分布, 同时主题看作是在词上的多项分布. 然而短文本由于缺乏足够的上下文信息, 使得其在传统主题模型上表现出数据稀疏的问题. 为解决这个问题, Chen等^[5]提出一种基于LDA与K近邻的短文本分类算法, 算法利用生成主题概率模型使其更关注于文本的语义关系, 并利用主题-词矩阵及其分词信息来度量两篇短文本之间的主题相似度, 一定程度上减缓了数据稀疏的问题. 但是K近邻的计算过程导致部分文本分类不准确的问题. Papanikolaou等^[6]在带标签的主题模型LLDA (Labeled-LDA)上引入了子集LLDA方法, 扩展了带标签的LDA算法主题模型, 它不仅可以有效地解决成千上万个标签的问题, 而且在预测精度方面比LLDA的最新技术有所提高. Cheng等^[7]提出一种BTM (Biterm Topic Model)模型, BTM通过直接对语料库中词对共现模式(即位词)进行建模来学习主题, 利用丰富的语料库级信息有效地进行推理. 学者们还提出了一些其他可行的方法: (1)根据元数据如用户标签^[8]、用户位置等将短文本聚合成长的伪文档^{[9, 10]}. 这个方法存在的缺陷是有的数据没有或者很难找到元数据. (2)限制主题的分布^[11], 即每一篇文档只属于一个主题. 但这些方法都只使用了词共现的方法, 而没有充分地考虑到词的语义关系. Li等^[12]引入GPU (General Pólya Urn)模型, 并结合DMM模型提出GPU-DMM (GPU-Dirichlet Multinomial Mixture)方法, 该方法通过引入词嵌入的方法对外部语料库进行训练, 利用GPU模型来提升词之间的语义关系, 从而解决语义关系不足的问题. Liang等^[13]提出GLTM (Global and Local word embedding-based Topic Model)模型, 模型同样引入词嵌入但将其分为全局词嵌入与局部词嵌入进一步增强了词的语义信息, 提高采样词与语义相关词的主题相关性. 然而该语义增强模型没有考虑词相关性强弱的问题, 对所有的主题语义相关词进行了增强, 使得主题相关性不够紧密, 对外部语料库进行训练得到的全局词嵌入向量与短文本数据集训练的局部词嵌入向量存在维数、语义信息不一致等问题.

本文提出STMSE (Short text Topic Model based on Semantic Enhancement)模型, 模型从两个方面进行改进: 首先对外部语料库进行词的全局词嵌入向量训练, 并计算全局词嵌入向量间的余弦相似度, 对收集的短文本数据进行词的局部词嵌入向量训练, 并计算局部词嵌入向量间的余弦相似度, 然后进行词向量融合计算得到词间的语义相关度, 从而解决语义信息不一致和向量维数不同的问题; 其次在主题词采样过程中选出与采样词语义相关性较强的词, 并计算词的主题语义相关词权重从而进行词语义增强. 最后将提出的STMSE模型与BTM, GPU-DMM, GLTM模型在数据集Web Snippets和Amazon Review上进行对比实验, 实验结果表明提出的STMSE模型在主题一致性与文本分类问题上有更好的表现.

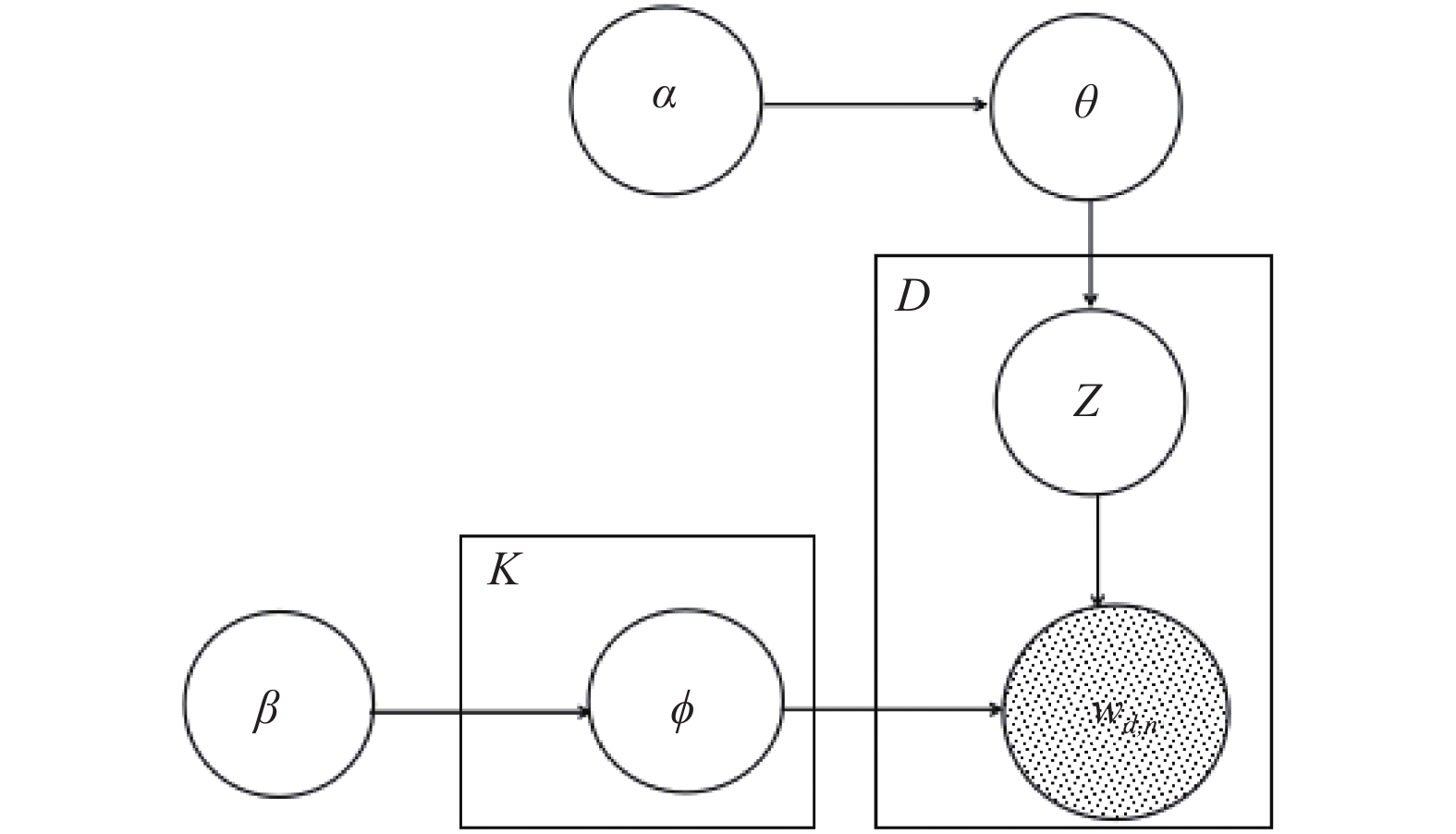
1 STMSE模型 1.1 DMM主题模型

生成模型认为一篇文章中的每个词都是通过“以一定概率选择某个主题, 并从这个主题中以一定概率选择某个词语”这样的一个过程得到. DMM就是一种生成概率模型, 并且认为每个文档都是由单个主题生成的^[14], 也就是说文献集中的每一篇文档只有一个主题. 给定文献集D, 文献集中的文档d, 词汇表V和预定义的主题数K. 假设每个文档d都只与一个特定的主题k相关. 文档d中的 ${N_d}$ 个词 $\{ {w_{d,1}},{w_{d,2}}\cdots,{w_{d,{N_d}}}\}$ 由主题-词多项分布 $p(w|{\textit{z}}=k)$ 独立生成, 表示为 ${\phi _k}$ , 且 $p(w|{\textit{z}}=k)$ 服从参数为β的先验Dirichlet分布. 文档的主题服从多项式分布, 表示为 $p({\textit{z}}=k)={\theta }_{k}$ , 其中k=1,… K, 且 $\displaystyle\sum\nolimits_k {{\theta _k} = 1} $ , 主题概率服从参数为α的先验Dirichlet分布. DMM生成过程如算法1.

算法1. DMM生成过程

1. 采样主题概率分布 $ \scriptstyle\theta \sim Dirichlet(\alpha )$

2. 对于每个主题 $\scriptstyle k \in \{ 1,\cdots, K\} $

采样主题-词项分布 $\scriptstyle {\phi }_{k} \sim Dirichlet(\beta )$

3. 对于每个文档 $\scriptstyle d \in \{ 1,\cdots, D\} $

(1) 采样主题 $ \scriptstyle{{\textit{z}}}_{d} \sim Multionmial(\theta )$

(2) 遍历每个词 $\scriptstyle w \in \{ {w_{d,1}},\cdots,{w_{d,{N_d}}}\} $

采样词 $\scriptstyle w \sim Multionmial({\phi }_{{{\textit{z}}}_{d}})$

算法1中隐藏变量 ${\varphi _{{{\textit{z}}_d}}}$ 通过Gibbs Sampling过程进行推断. 图1为DMM模型的概率图模型.

1.2 语义增强

传统主题模型主要是通过词之间的共现模式即两个词出现的次数与前后位置等来确定词语之间是否相关. 但仅以这种方法计算词语之间的相关性不能充分捕捉短文本的上下文信息, 而且不适用于短文本, 因为具有较高语义相关度的单词可能不会在相同的短文本中频繁出现. 而词嵌入可以保留单词的上下文信息, 故而学习的单词可以捕获一般单词的共现模式^[15], 即语义或句法上相关的单词在潜在空间中会被映射得更近. 在文献[16,17]中引入了词嵌入的方法, 通过词嵌入的方法计算词与词之间的语义相关度. 为了能够更好的计算词之间的语义相关度, 本文利用外部知识(谷歌语料)进行词嵌入训练, 为全局词嵌入. 对实验数据集进行嵌入学习, 获得短文本上下文的语义特征信息, 为局部词嵌入, 然而全局词嵌入训练的词向量与局部词嵌入训练的词向量存在语义信息不兼容的问题且嵌入向量维数存在较大的差距, 因此提出通过向量融合计算词向量间的语义相关度来解决这个问题.

通过全局词嵌入向量和局部词嵌入向量对词进行余弦相似度计算, 进而计算出词的语义相关度. 向量间的余弦相似度用下式计算:

$ sim(w,{w}_{i})=\mathrm{cos}(v(w), v({w}_{i}))=\frac{v(w)\cdot v({w}_{i})}{\Vert v(w)\Vert \ast \Vert v({w}_{i})\Vert }$

(1)

其中 $sim(w,{w_i})$ 表示词w与词 ${w_i}$ 的余弦相似度, $v(w)$ 为词w的向量表示. 通过式(1)计算全局词嵌入向量的余弦相似度 $si{m_g}(w,{w_i})$ 与局部词嵌入的余弦相似度 $si{m_l}(w,{w_i})$ , 通过式(2)计算两个词之间的语义相关度:

$SR(w,{w_i}) = \frac{1}{2}(si{m_g}(w,{w_i}) + si{m_l}(w,{w_i}))$

(2)

其中, $ SR(w,{w}_{i})$ 表示词w和词 ${w_i}$ 的语义相关度.

根据词的语义相关度构建词w的语义相关词集 $ {M}_{w}=\{{w}_{i}|{w}_{i}\in V, SR(w,{w}_{i})>\epsilon \}$ . 对采样词w的语义相关词集 ${M_w}$ 中的 ${w_i}$ 应用式(3)计算语义提升矩阵 ${A_{w,{w_i}}}$ . 具体公式如式下:

${A_{w,{w_i}}} = \left\{ {\begin{array}{*{20}{l}} 1,&{w = {w_i}} \\ {{\mu _{w,{w_i}}}}, &{{w_i} \ne w,{w_i} \in {M_w}} \\ 0,&{\rm else} \end{array}} \right.$

(3)

一般来说, 按照词的语义相关度值降序排序后靠后的词对主题模型的贡献率不大, 所以只对语义相关词集 ${M_w}$ 中的语义相关度较高的部分词做语义提升. 故先将 ${M_w}$ 中词对的语义相关度值按降序排列, 并取前num个词进行语义提升, 计算语义提升矩阵 ${A_{w,{w_i}}}$ 中的语义相关词权重 $\;\mu _{w,{w_i}}^{}$ , 如式(4):

$\mu _{w,{w_i}}^{} = \frac{{SR(w,{w_i})}}{{\displaystyle\sum\limits_{i = 1}^{num} S R(w,{w_i})}}$

(4)

由此获得语义增强的相关词权重. 通过利用GPU模型思想进行词的语义增强, 即对于采样词, 增加与其主题语义相关性强的词的个数, 从而增强语义相关词与主题词间的关系, 计算如式(5)、式(6):

$n_k^{{w_i}} = n_k^{{w_i}} + N_d^w{A_{w,{w_i}}}$

(5)

$n_k^{} = n_k^{} + N_d^w{A_{w,{w_i}}}$

(6)

其中, $n_k^{{w_i}}$ 表示与主题k相关的词 ${w_i}$ 的统计量, $N_d^w$ 表示文档d中出现词w的个数, ${n_k}$ 表示与主题k相关单词的统计量.

1.3 主题模型推断

主题模型推断的Gibbs Sampling过程如下: 在每一轮迭代过程中, 采样一篇文档并记录相关统计量; 为采样的文档重新采样一个新的主题, 更新文档的相关统计量, 并对采样词的语义相关词进行语义增强计算. 对于文档中的每个词, 并不是对所有的词进行语义提升, 因为在文档中不是所有的词都与主题存在很强的关联, 其中存在一定的噪音词, 因此需要计算主题与单词的相似性来判断是否对采样词进行语义提升. 通过计算采样主题与采样词的语义相关度, 如果相似度SR(z, w)>ε, 则对采样词进行增强计算. 其中为每一篇文档采样一个主题遵从条件概率:

$ \begin{split} p&\left( {{{\textit{z}}}_{}=k|{\overrightarrow{{\textit{z}}}}_{\neg d},\overrightarrow{d}} \right)\propto \\ &\frac{{m}_{k, \neg d}+\alpha }{D-1+K\alpha }\ast \frac{{\displaystyle {\prod }_{w\in d}}{\displaystyle {\prod }_{j=1}^{{N}_{d}^{w}}\left( {{n}_{k, \neg d}^{w}+\beta +j-1} \right)}}{{\displaystyle {\prod }_{i=1}^{{N}_{d}}{n}_{k,\neg d}^{}+\left|V\right|\beta +i-1}} \end{split}$

(7)

其中, ${m_k}$ 是与主题k相关的文本数. 下标 $\neg d$ 表示不包括文档d. 采样算法完成后, 对模型中的主题-词项后验概率分布 $p(w|{\textit{z}}=k)$ 进行计算, 如式(8):

$ p(w|{\textit{z}}=k)=\frac{{n}_{k}^{w}+\beta }{{n}_{k}+\left|V\right|\beta }$

(8)

STMSE模型的Gibbs Sampling算法过程如算法2.

算法2. Gibbs Sampling

输入: 主题数K,α,β, $\scriptstyle{M_w}$ 和短文档集D

输出: 主题-词后验概率分布

1. 初始化数据统计量

在每一轮迭代过程中

2. 在文档集D中采样一篇文档d,

(1)更改与主题相关的文档的个数, $\scriptstyle{n_k} = {n_k} - 1$ ;

(2)对于文档d中的词w, 即 $\scriptstyle w \in d$ , 更新相关统计量: $\scriptstyle n_k^w = n_k^w - N_d^w$ , $\scriptstyle n_k^{} = n_k^{} - N_d^w$ ;

(3)对于 $\scriptstyle{w_i} \in {M_w}$ , 计算语义提升矩阵 $\scriptstyle{A_{w,{w_i}}}$ 并更新相关统计量 $\scriptstyle n_k^{{w_i}} = $ $ \scriptstyle n_k^{{w_i}} - N_d^w{A_{w,{w_i}}}$ , $\scriptstyle n_k^{} = {n_k} - N_d^w{A_{w,{w_i}}}$ ;

3. 根据式(7)为文档d重新采样一个新主题z,

(1) 更改与主题相关的文档的个数 $\scriptstyle{n_k} = {n_k} + 1;$

(2) 对于词 $\scriptstyle w \in d$ , 如果SR(z, w)> $\scriptstyle\varepsilon $ , 更改相关统计量 $\scriptstyle n_k^w = n_k^w + N_d^w$ , $\scriptstyle n_k^{} = n_k^{} + N_d^w$ ;

(3)对每个 $\scriptstyle{w_i} \in {M_w}$ , 计算语义提升矩阵 $\scriptstyle{A_{w,{w_i}}}$ 并更新相关统计量 $\scriptstyle n_k^{{w_i}} = $ $ \scriptstyle n_k^{{w_i}} + N_d^w{A_{w,{w_i}}}$ , $\scriptstyle n_k^{} = n_k^{} + N_d^w{A_{w,{w_i}}}$ .

2 实验分析 2.1 实验数据与参数设置

本文使用Web Snippets数据集和Amazon Review数据集进行验证. 其中Web Snippets数据集包括12340个搜索片段, 每个片段属于8个类别中的一个类别. Amazon Review数据集是一系列从1996年5月到2014年7月的亚马逊产品评论, 其中每个片段属于7个类别中的一个类别, 本文从中随机采样20000条数据作为本文的数据集. 对上述两个数据集进行预处理, 经过数据预处理后的数据集信息如表1所示.

统一设置公共参数值 $\alpha = \dfrac{{50}}{K}$ 、 $\;\beta = 0.01$ , $\varepsilon $ 设置为0.5、最大迭代轮次为1500次. 全局词嵌入用谷歌语料库进行训练, 嵌入空间维度设置为300维. 局部词嵌入使用实验数据集进行训练, 嵌入空间维度设置为30维. 训练嵌入工具用谷歌Word2Vec开发工具Skip-gram模型. 本文选取num的值为10 (与下文实验中给出的主题-词项分布排列所取个数一致). 实验通过短文本分类与主题模型一致性来评估本文提出的STMSE模型的效果, 并与BTM、GLTM和GPU-DMM模型进行对比.

2.2 模型评估与分析 2.2.1 短文本分类

在短文本分类实验中, 根据主题模型的结果, 每篇文档可表达为主题分布 $p({\textit{z}}|d)$ , 即每篇文档可以表示成一个向量分布. 用支持向量机做分类器, 并使用其默认参数, 进行文档分类实验, 文档的分类正确率越高, 主题模型学习到的主题结果就越合理, 主题之间的区分度也就越高, 分类实验的执行效果就越好. 文献[12]中提到两种文档主题条件概率分布的推断方法:

Naive Bayes (NB) rule:

$p({\textit{z}} = k|d) \propto p({\textit{z}} = k)\prod\limits_{i = 1}^{{N_d}} {p({w_i}|{\textit{z}} = k)} $

(9)

Summation over Words (SW):

$p({\textit{z}} = k|d) \propto \sum\limits_w {p({\textit{z}} = k|w)p(w|d)} $

(10)

其中, $p(w|d)$ 可以用文档d中出现的词w的次数来估计, $p({\textit{z}} = k|w)$ 可以由贝叶斯准则推断:

$p({\textit{z}} = k|w) \propto p({\textit{z}} = k)p(w|{\textit{z}} = k)$

(11)

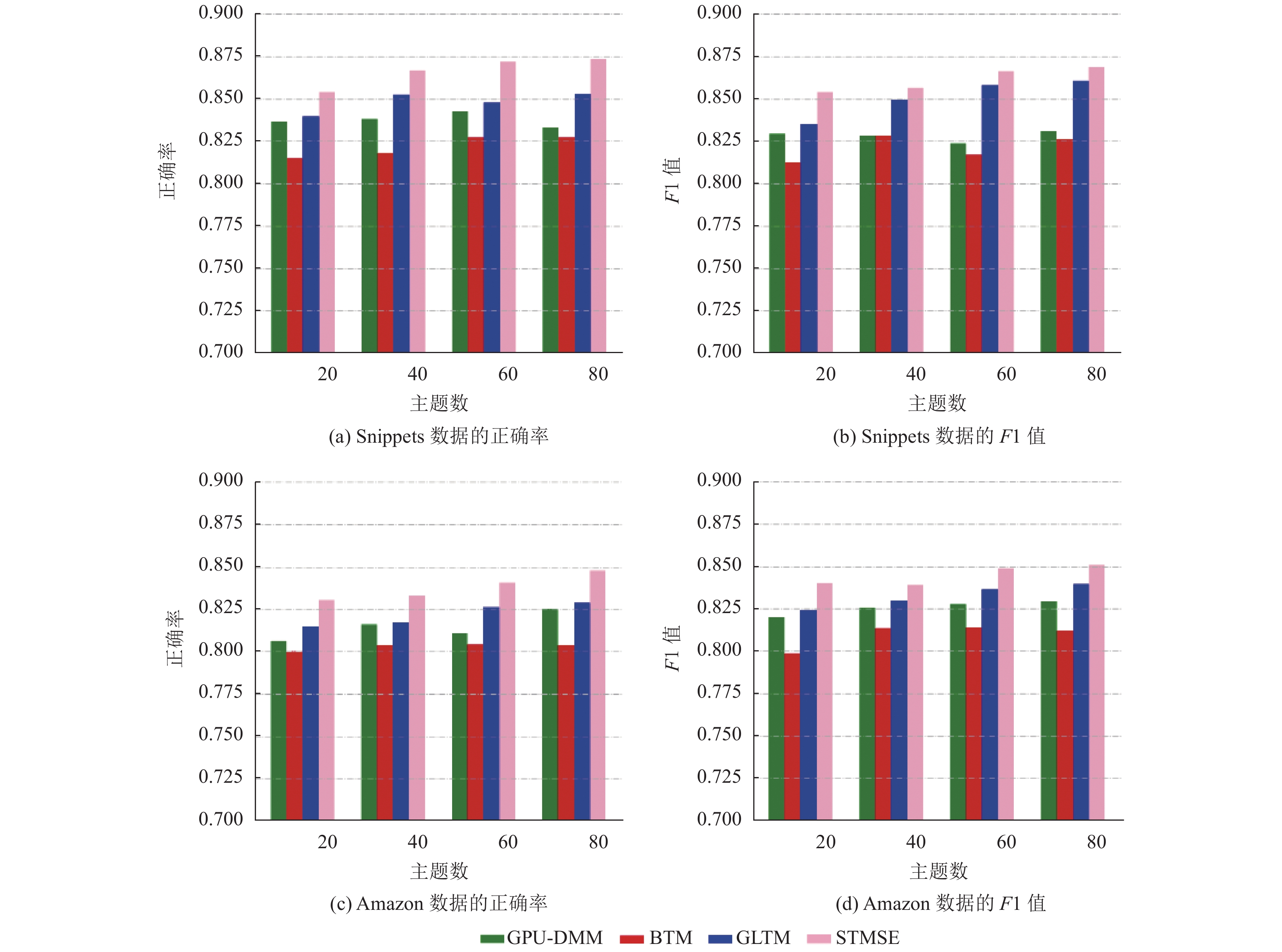
本文采用SW方法来获得文档的主题概率分布. 图2为提出的STMSE模型与其他基线模型在分类正确率上的实验结果比较. 其中F1值为式(12)所示:

$F1 = \frac{{2 \times {{precision}} \times {{recall}}}}{{{{precision}} + {{recall}}}}$

(12)

从图2(a)与图2(c)中可看出, 本文提出的STMSE模型在分类效果上得到了较好的结果, 在两个数据集上的分类效果比其他模型的都要好. 对比图2的4个子图能够发现: 由于Amazon Review数据集在数据预处理之后的平均文本长度要稍微长一些, 具备更丰富的上下文语义, 故而在Amazon数据集上的实验结果比在Snippets数据集上的效果要稳定, 此外这与语料库的质量也有一定的关系. GLTM模型进行了全局与局部词的嵌入训练, 导致在进行训练模型的相似度计算上存在一定的数据相似度的冗余计算, 因而在进行语义增强的时候没能将主题进行更好的分类, 故而分类准确率相对本文提出的模型较差. 而GPU-DMM模型因为只进行了外部语料库的词嵌入训练, 没有对训练集进行词嵌入训练来获取上下文信息, 同时也没有根据词的语义权重进行语义提升故而实验效果没有GLTM的好; 而BTM模型的分类效果最差, 是因为利用词对在建模过程中, 词对共现使得主题的区分性相对变弱了一些, 只使用短文本中的词也使得主题的相关信息比较稀疏, 主题识别具有一定的局限性, 使得分类效果差. 但从图中BTM的数据可以得知, 直接使用词对进行主题建模时, 使得BTM模型的稳定性比其他模型要好.

2.2.2 主题一致性

主题一致性表明如果一个主题中最可能出现的词在语料库中出现的频率更高, 那么这个主题就更加一致. 这个想法与BTM模型的基本假设一致, 即更经常同时出现的词应该更属于同一个主题. PMI-Score利用外部源(例如, 维基百科)的大规模文本数据集, 基于点态互信息来测量主题相关性, 因这些外部源数据集与模型无关, 故而PMI-Score对所有主题模型都是公平的. 因此, 实验利用PMI-Score来验证主题一致性.

给定主题k和该主题概率排序在前T的词 $(w{}_1,\cdots, $ $ {w_T})$ , 主题k的PMI值的计算公式如下:

$PMI - Score(k) = \frac{1}{{T(T - 1)}}\sum\limits_{1 \le i \le j \le T} {PMI({w_i},{w_j})} $

(13)

$PMI({w_i},{w_j}) = \log \frac{{P({w_i},{w_j})}}{{P(w{}_i)P({w_j})}}$

(14)

其中, $P({w_i},{w_j})$ 为词对 ${w_i}$ 和 ${w_j}$ 在外部数据集(如维基百科)中共现的概率, $P({w_i})$ 为词 ${w_i}$ 在外部数据集中出现的概率. 每个模型的主题一致性是所有学习到的PMI-Score的平均值.PMI-Score值越高, 主题一致性就越好. 实验给出在主题-词项分布排列前10的主题词, 主题个数K分别为20, 40, 60, 80上的主题一致性评估结果. 实验结果如图3所示.

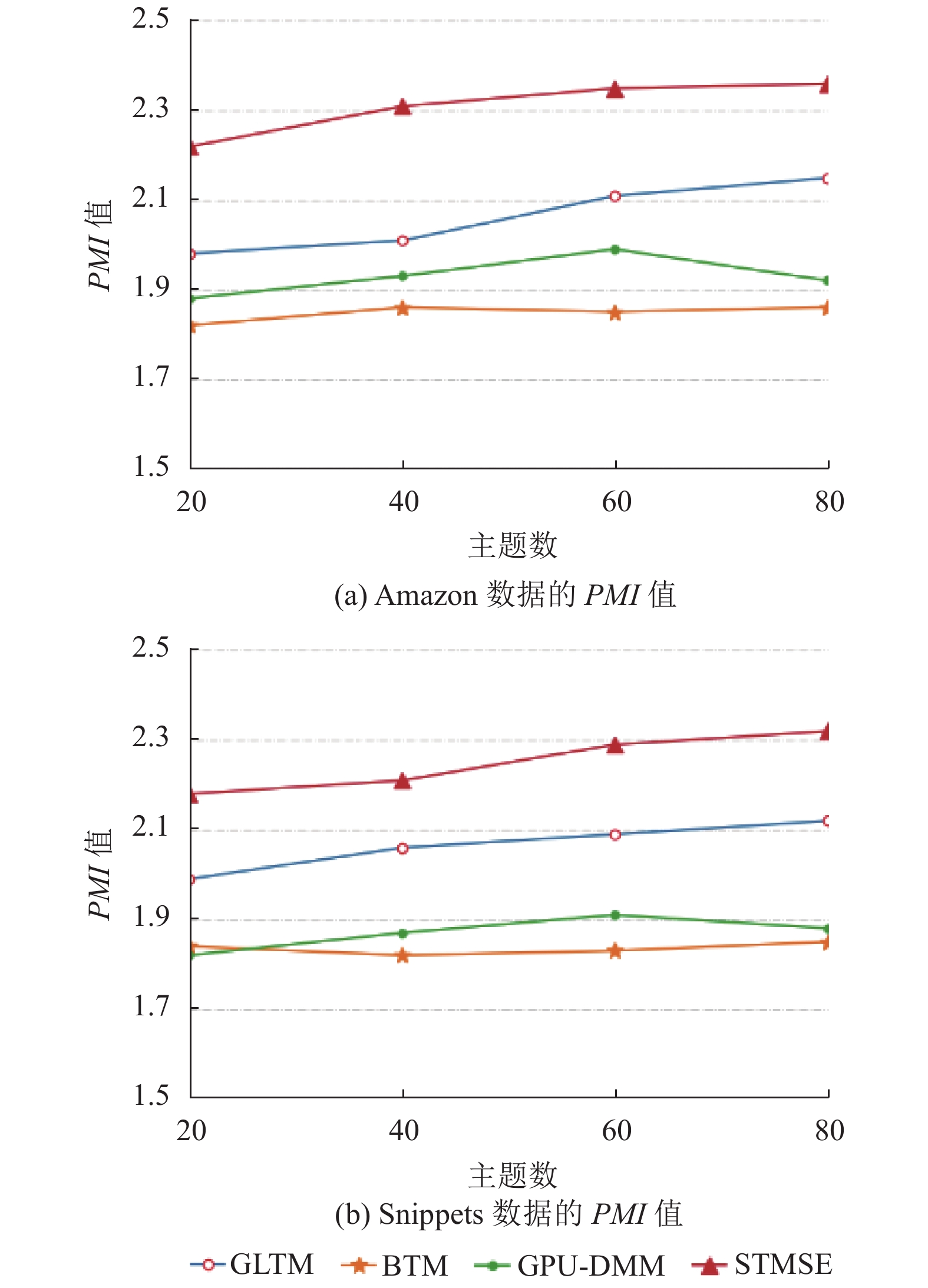
从图3(a)与图3(b)可以看出, 提出的STMSE模型在主题一致性上表现出了良好的结果, 都优于其他主题模型. 是因为模型结合了外部知识训练的全局词嵌入和短文本训练的局部词嵌入并进行了向量的融合计算, 提高了语义表示能力和更为准确的主题语义, 根据词的相关度强弱进行了词的权重比语义增强, 加强了词间的语义关系. 实验结果在Amazon数据集上比在Snippets数据集上表现出更好的效果, 原因是Snippets比Amazon有更高的数据稀疏性.

BTM模型取得了最差的结果, 由于训练过程采用了词对的模式, 所以在主题区分上的效果没有其他模型效果好. 但BTM主题模型在建模时是通过词对共现模式来完成的, 保留了一部分语义相关词集以及上下文信息, 增强了语义间的关系, 给模型带来了一定的稳定性. 在两个数据集上都表现出相当不错的效果, 且随着主题数的增加, 主题一致性波动不大. GPU-DMM模型相对BTM模型来说在主题一致性实验上有的结果要好, 是因为GPU-DMM模型考虑到上下文相关信息, 同时也考虑词汇的语义相关度并增强语义相关度. 但当主题数量增多时, 主题一致性开始会随着主题数量的增多效果会变的更好, 这是因为主题数量的增多使得语义信息的表达更为充分, 而当主题数再增多时, 就使得语义的稀疏性变得更强, 因此这时增加主题数量使得主题一致性表现变得更差. GLTM模型利用了外部知识库进行了语料的训练从外部知识中获得的词的共现词较多, 并结合短文本的上下文信息进行结合分析, 实现了在数据集上的主题一致性, 取得了次优的结果.

3 总结

本文利用全局词嵌入与局部词嵌入进行模型训练, 以获得外部知识与文本的上下文信息, 并根据嵌入向量计算词的语义相关度, 以更好的表达词之间的语义关系; 其次计算语义相关度提升矩阵, 对词进行语义增强, 使得同属于一个主题的单词之间联系更加紧密; 实验表明, 本文提出的模型在文本分类与主题一致性实验上要优于其他基线模型, 在短文本主题模型构建中具有良好的表现, 对于短文本的信息分类有很高的应用价值.