2. 中国科学院大学, 北京 100049;
3. 中国工业互联网研究院, 北京 100102;
4. 中国科学院 软件研究所, 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. China Academy of Industrial Internet, Beijing 100102, China;
4. Institute of Software, Chinese Academy of Sciences, Beijing 100190, China
科研组织是学术创新的主体, 在学术创新中科研合作及学术交流发挥着越来越重要的作用, 研究者将自身的科研知识、经验和资源进行共享, 为其他研究者提供更多的灵感和思路, 创造出更多更有价值的科研成果. 因此, 挖掘出研究者之间隐含的关联关系, 寻找相关学术社区, 是值得重点关注的问题.
传统的学术社区多是着眼于研究者科技成果产生的关联进行社区发现, 忽略了研究者自身学术活动产生的关联, 如何获取并利用相关学术信息进行社区发现是本研究的重点. 随着科技信息的爆炸式增长, 不同于传统的论文数据, 科技信息数据种类更加丰富, 包括科技成果数据、科技实体数据、科技活动数据等. 在此背景下, 越来越多的学术资源网络平台应运而生, 通过科研人员唯一身份标识[1]将研究者及其学术活动信息进行关联, 如Researcher ID[2], 帮助研究者对其出版文献进行管理, 注重对研究者著作的展示; ISNI (International Standard Name Identifier, 国际标准名称标识符)[3], 将媒体内容的贡献者赋予唯一标识, 标识相同参与者在媒体价值链上的不同身份; ORCID (Open Research and Contributor ID, 开放研究者与贡献者标识)[4], 将研究者及其学术活动精确关联, 记录研究者各项科研动态, 并与相关科研管理系统、文献数据平台、机构数据库相连接. 通过这些标识体系形成了一种底层连通的信息枢纽机制, 促进相关信息在不同系统中的流动, 可以更为便捷的得到研究者的各项学术活动及学术资源的信息[5].
因此, 本文使用ORCID获取研究者相关学术信息, 构建学术信息网络, 分析研究者通过不同学术活动产生的关联, 并针对网络中存在的异质性和网络层次带来的挑战, 提出一种基于加权跨层边聚类系数的社区发现模型, 挖掘出网络背后隐藏的社区结构[6], 在提高划分效果的同时对科技实体的推荐、评价、学科交叉和学科演化等相关研究均有重要意义[7].
本文余下章节中, 第1节对涉及到的相关工作进行概述, 第2节介绍基于ORCID的社区发现模型, 第3节对所提方案进行实现并对结果进行分析, 第4节总结全文并对未来的发展与挑战做出简要分析.
1 相关工作如何构建学术信息网络以及如何利用学术信息进行社区发现是我们需要关注的重点.
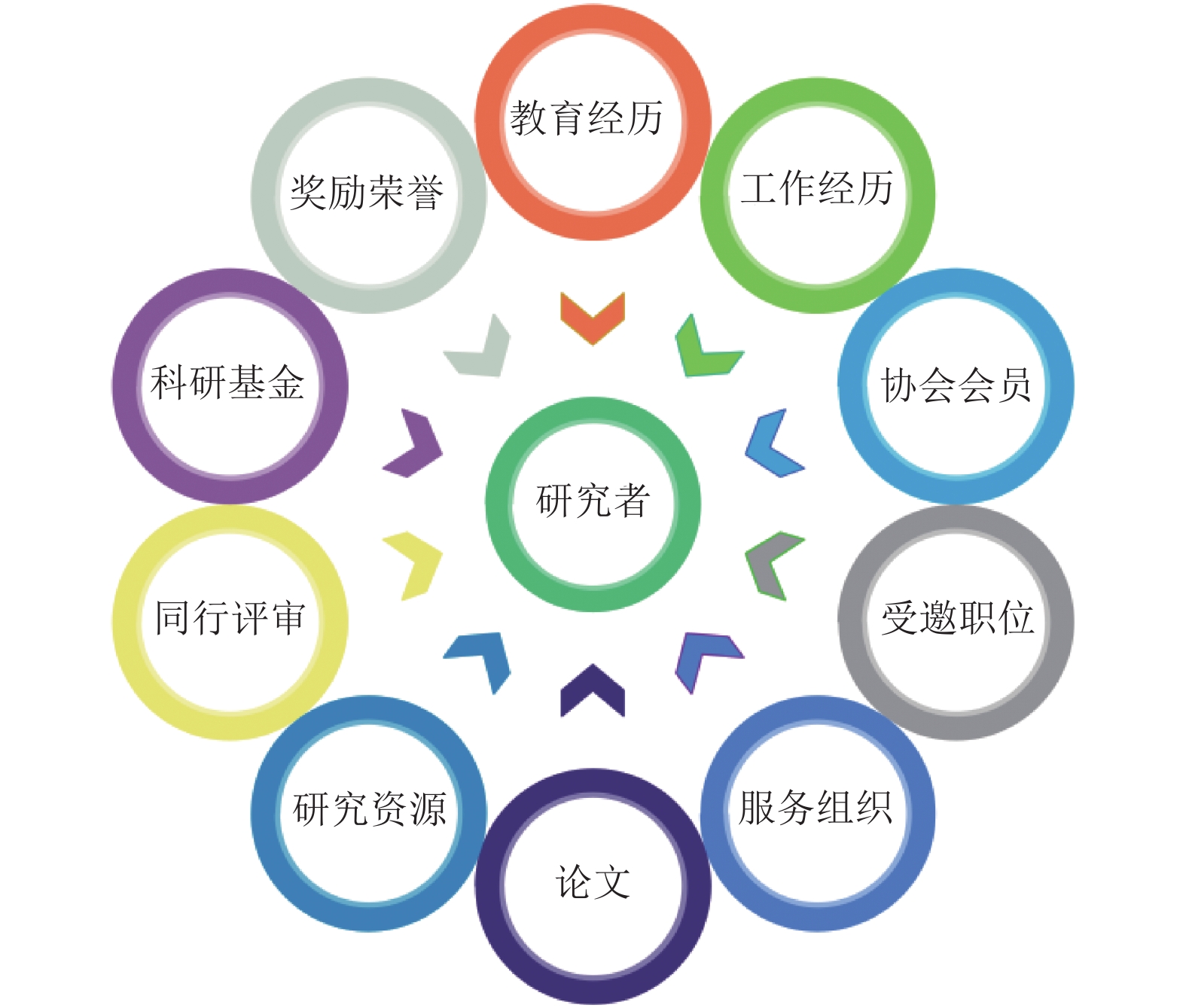
针对学术信息网络的构建, 科研人员唯一标识符发挥了重要的作用[8], 科研人员唯一标识符能够实现对科研人员的有效标识, 提升科研成果检索效果, 便于管理科研成果和个人档案, 也可以通过对其他科研人员的信息的追踪达到寻找合作伙伴的目的, 还能将科研人员及其所属机构、参与的科研项目甚至是其他学术内容生产价值链中的潜在关联实体相链接, 从而实现科研生态系统中不同要素之间的紧密相连[9], 也可以接入相关科技领域大数据知识图谱平台[10]实现对科研数据的有效利用. ORCID, 开放研究者与贡献者标识, 以人为中心, 为全球每位研究者分配一个终生有效的唯一身份标识, 并以此为基础, 把研究者所有相关的科研活动与成果都精确地匹配并连接起来, 提高了科研人员档案的准确性. 每一位研究者ORCID记录中可以关联的信息包括教育经历、工作经历、发表论文、学协会会员、荣誉与奖励、大会报告、审稿贡献、科研基金等, 如图1所示.
图1中该编码采用16个数字表示, 每个编码分为4组显示, 如0000-1234-5678-0000. 目前ORCID注册量已经超过5000000个, 有超过600家学术图书馆、研究机构、资助机构和出版商会使用这些ID来跟踪数据, 也用于对研究者的研究成果进行追踪. 因此, 如何利用ORCID获取的数据进行网络的构建是我们研究的第一个重点.
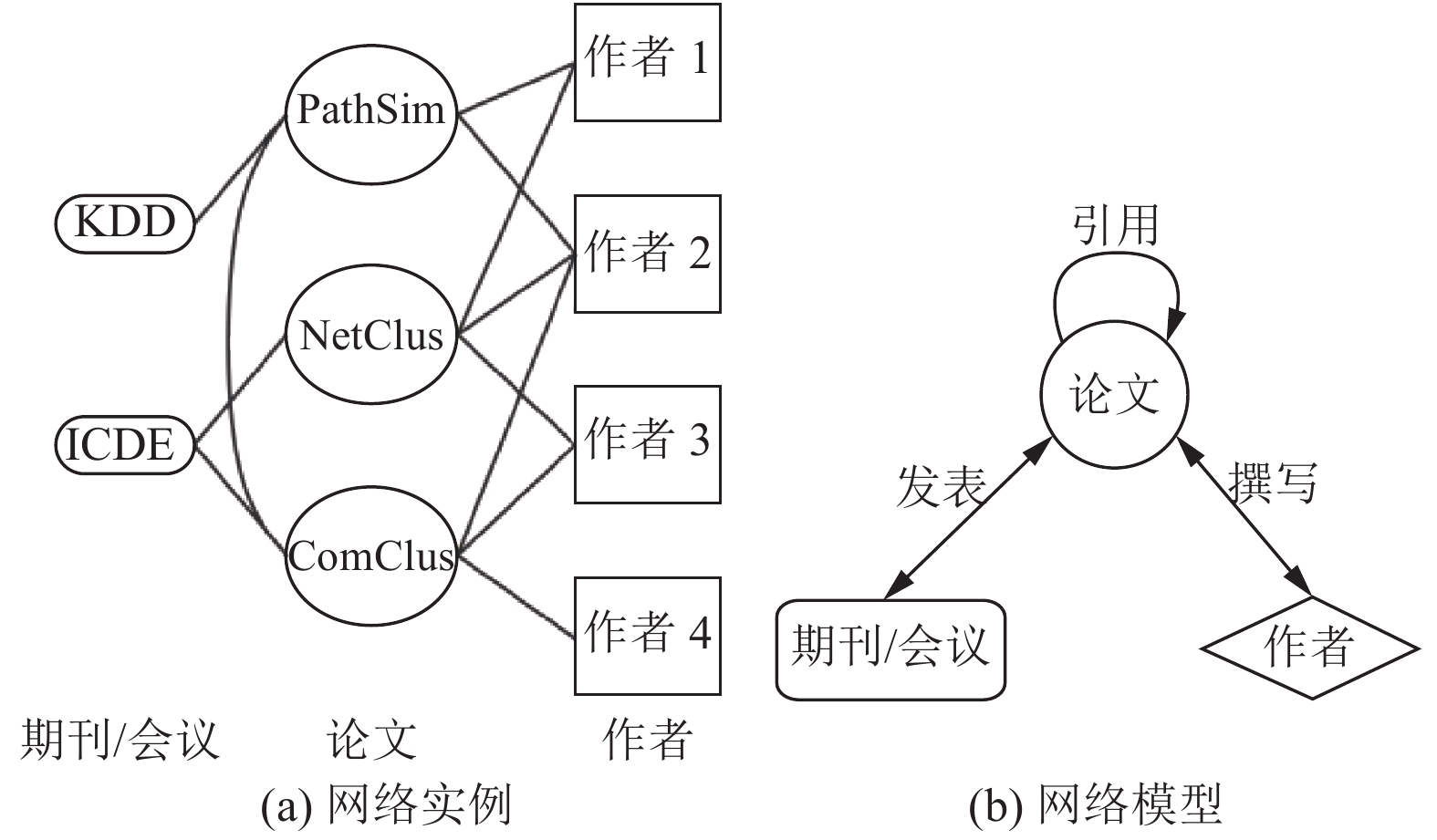
针对如何利用学术信息进行社区发现, 在传统学术社区发现中大多通过分析合著网络或引文网络寻找研究者之间的关联关系, 如图2, 网络中包含作者、论文、会议等异质节点.
|
图 1 ORCID数据内容 |
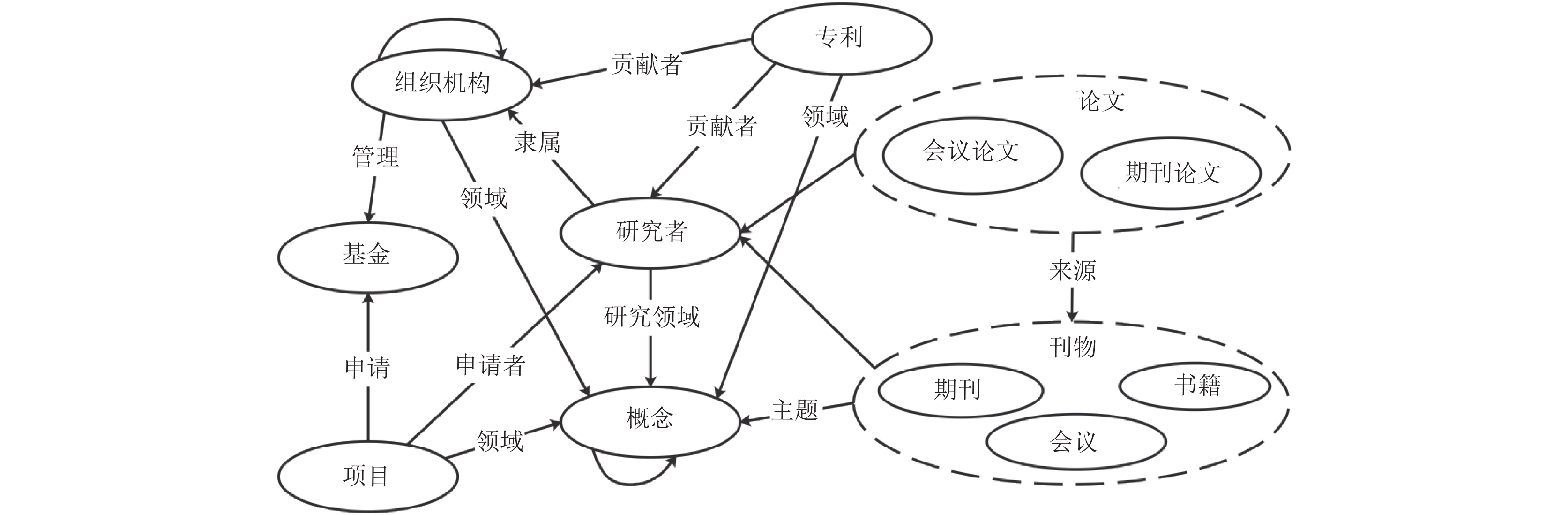
对于上述网络, NetClus算法[11]针对以论文为中心的星型学术网络, 利用排名提升聚类结果, 迭代调整每个对象的类别, 生成具有相同拓扑的输入网络的子网络合集, 每个聚类结果有相同的主题. PathSelClus算法[12]提出一种将元路径与聚类相结合的算法, 通过预先为每个聚类提供一部分种子节点, 系统学习到元路径的权重, 根据权重产社区, 叠加不同元路径的聚类结果生产最终社区. Lu等提出了Hete_MESE多维社区检测算法[13], 首先将异构信息网络中的多个实体类型之一指定为社区中心节点类型, 并相应地提取复用网络, 然后, 基于复用网络检测重叠的节点中心社区, 将其视为种子社区, 吸收其他实体类型以利用种子扩展产生异质社区. 文献[14]基于Salton方法计算作者间相似度以评估合著关系强弱, 将节点间的边作为聚类对象, 采用凝聚式层次聚类进行学术社区发现. 文献[15]以直接引用关系构建显性关联, 以引文抽取出的兴趣标签构建隐性关联, 用以衡量研究者之间关系的强弱从而进行社区发现. 而面对大规模的学术信息网络, 如图3, 网络中节点种类更多, 关联关系更复杂, 复杂的网络结构对社区发现带来了新的挑战.
|
图 2 合著网络示例 |
|
图 3 复杂学术信息网络 |
针对异质网络的社区发现研究已得到了学者的广泛关注, 本文重点阐述多层网络社区发现的相关研究成果. 文献[16]采用多目标方法, 在第一层应用经典社区发现算法, 对其余的连续层, 采用最大化当前层模块度和前一层划分的社区结构的相似性双目标优化方法来发现社区. 文献[17]对每一层网络应用经典社区发现算法并用集成聚类方法合并划分的社区来发现社区. 文献[18]提出了一种基于元路径嵌入的聚类方法MPEClus, 将原始网络转换为具有由元路径指定的拥有独立语义的多个子网, 使用近似通勤嵌入学习节点的向量表示, 并针对不同度量空间中学习的节点向量进行社区发现. 文献[19]使用基于频谱聚类和低秩矩阵分解的方法组合多层网络的多层信息来进行社区发现. 文献[20]通过使用跨层边聚系数计算节点间相似度并通过不断更新损失函数实现多层网络社区划分. 因此, 如何解决学术信息网络中异质性和网络层次带来的挑战, 从而进行社区发现, 也是我们需要研究的重点.
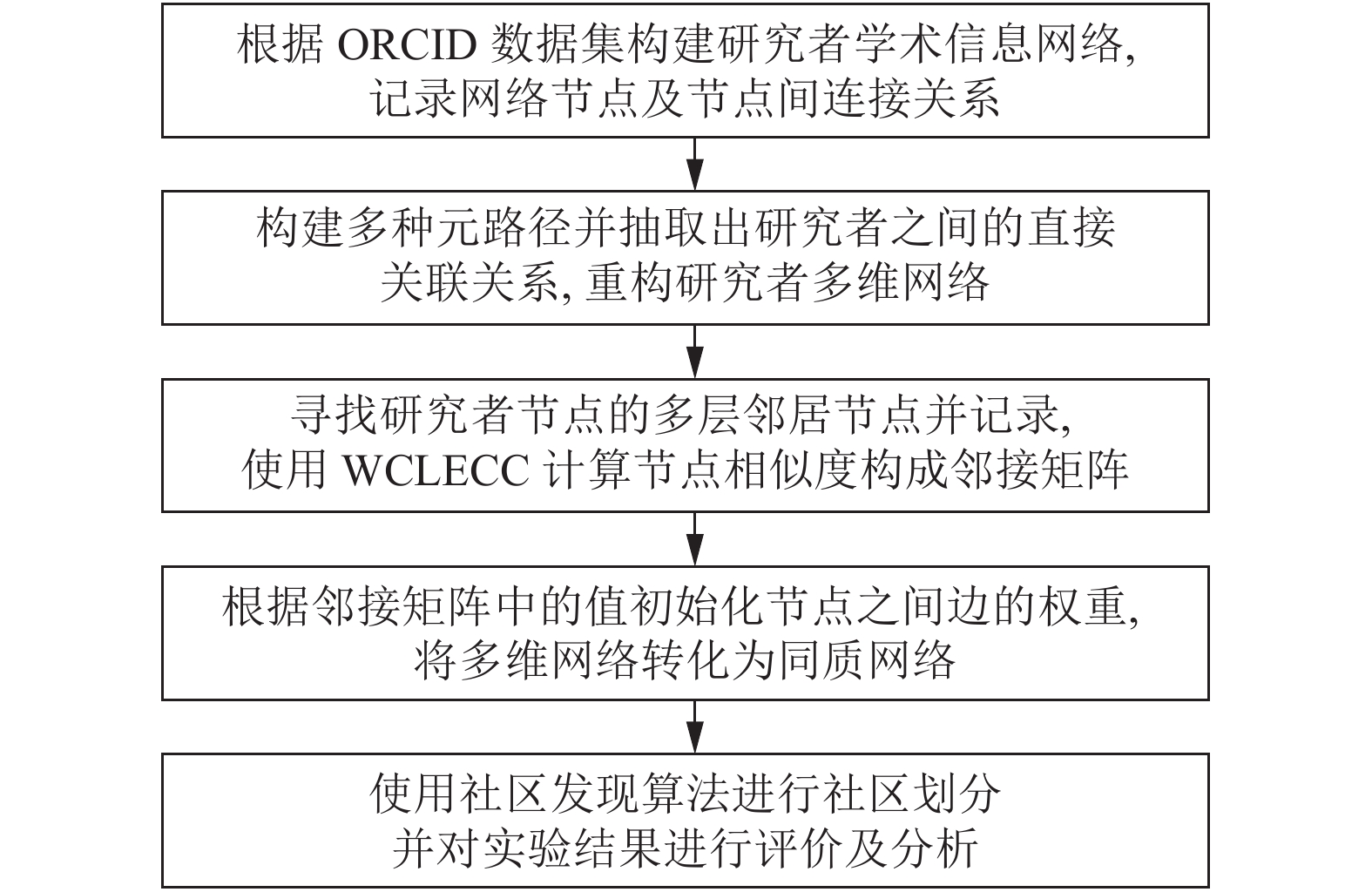
2 基于ORCID和加权跨层边聚类系数的社区发现模型本文基于ORCID获取的数据集, 分析研究者及其学术活动信息构建学术信息网络, 寻找研究者之间多属性的关联关系并计算研究者之间的相似度, 从而进行学术社区的发现, 本文算法流程图如图4所示.
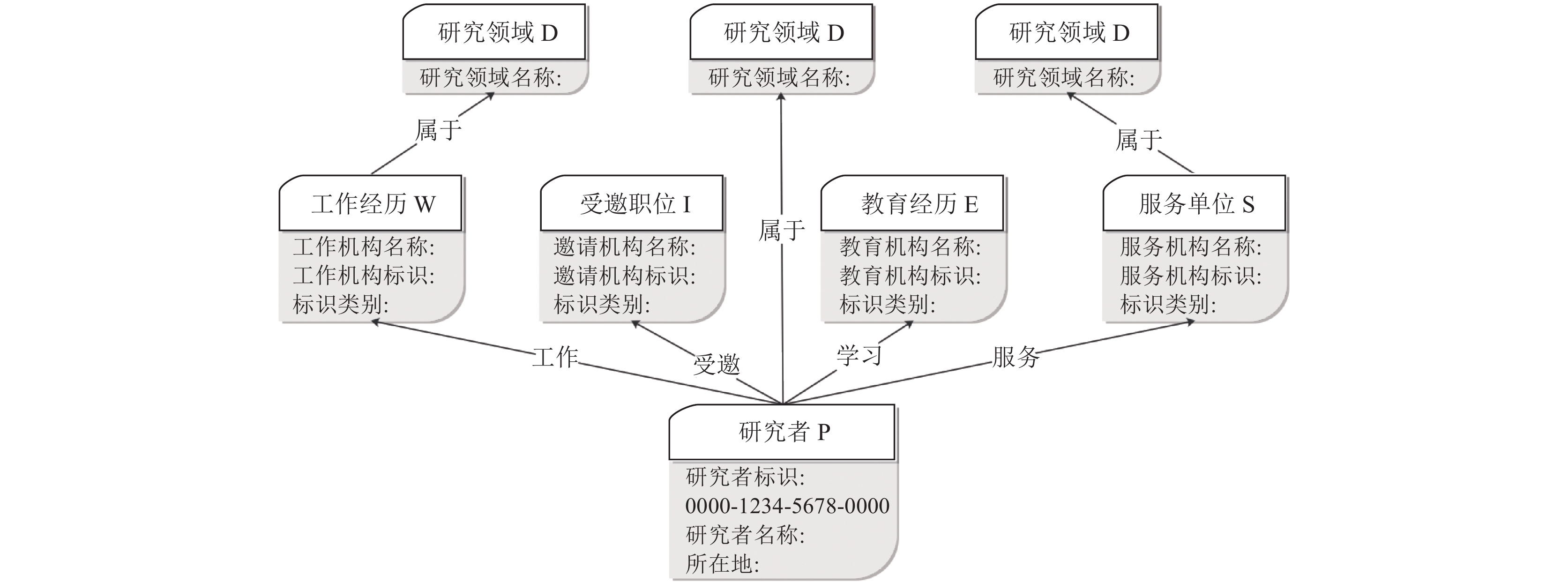
2.1 构建ORCID异质网络通过分析ORCID数据中包含的学术活动信息, 可以发现研究者之间通过不同学术信息可以产生多种关联, 将不同学术信息作为不同类型节点从而构建异质网络, 网络中包含研究者节点P, 教育经历节点E、工作经历节点W、受邀职位节点I、服务单位节点S、学术领域节点D, 如图5所示, 同时, 不同节点之间也存在不同类型的关联关系. 通过ORCID异质网络, 不仅可以快速获取研究者相关的学术活动信息, 也可以通过某些学术活动查询到相关联的研究者, 不同研究者通过中间学术活动节点也可以取得不同属性的关联.
|
图 4 基于ORCID的学术社区发现算法流程 |
|
图 5 ORCID异质网络 |
2.2 根据元路径抽取研究者多维异质网络
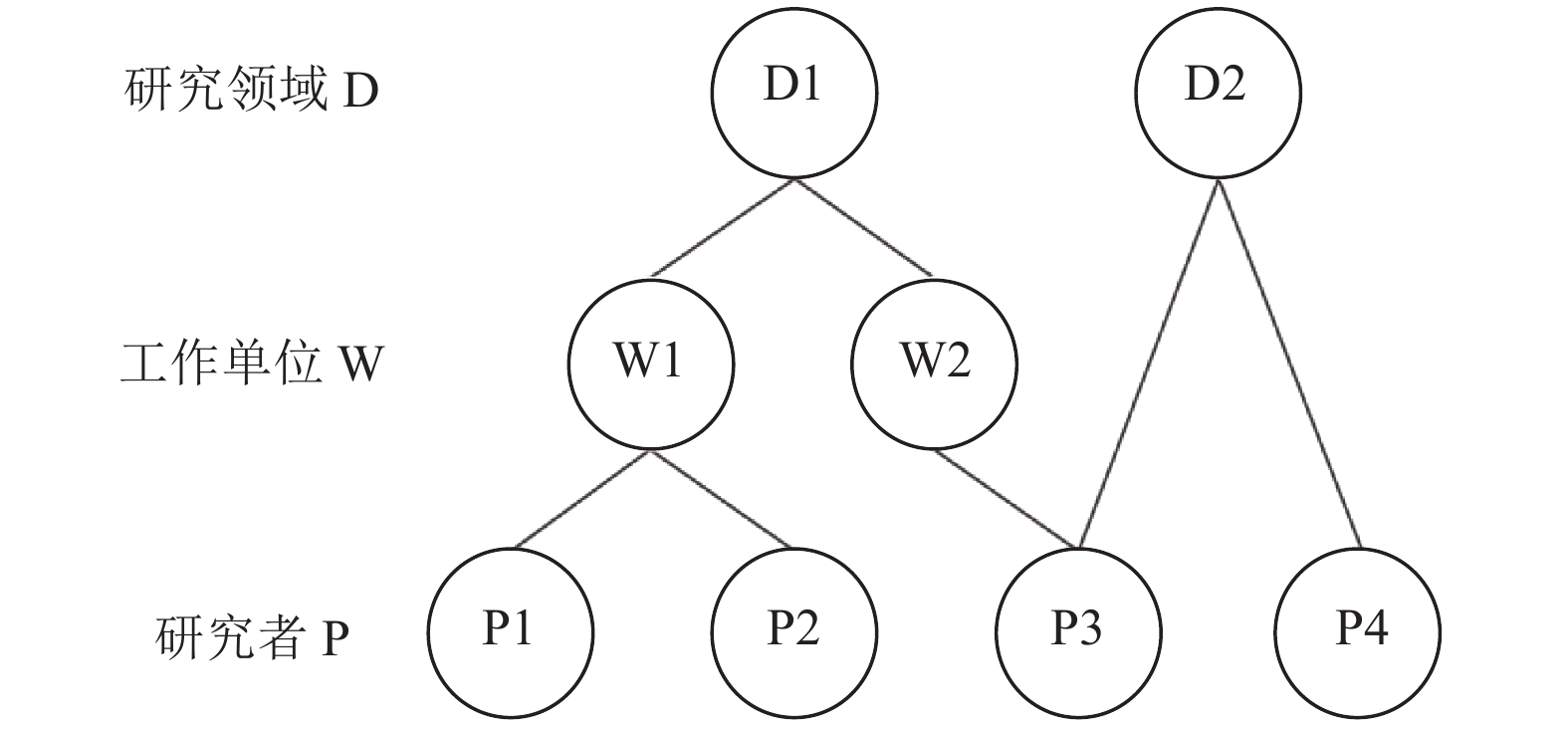
由于构建的ORCID异质网络中存在大量的学术活动节点, 研究者之间并非直接相连, 而是存在不同的路径. 不同路径连接的研究者之间存在不同语义的关联关系, 构成了多种元路径, 图6展示了ORCID异质网络中存在的部分元路径, P为研究者节点、D为研究领域节点、W为工作单位节点, P3D2P4表示P3和P4有相同的研究领域, P1W1P2表示P1和P2在相同的单位工作过, P1W1D1W2P3表示P1和P3有相同领域内的工作经历.
多种元路径的存在既无法直观发现研究者节点之间的关联关系, 也增加了计算研究者相似度的难度. 因此, 本文通过不同元路径提取出研究者节点之间的多种直接关联关系, 从而构成研究者多维异质网络, 网络中仅包含研究者节点一种节点和多种不同属性的边. 元路径选择如表1所示, 从而根据新的关联关系重构研究者多维异质网络, 解决了ORCID异质网络中节点多样性而产生的社区划分问题.
2.3 节点相似度计算基于研究者多维异质网络, 本文综合考虑研究者节点间的多种属性关联关系来计算多维网络中节点间的相似度. 本文考虑使用Brodka等提出的跨层边聚类系数CLECC[20]可以用来计算多维网络中节点间的相似度, 但是在计算过程中, 只能针对某一层次计算节点间相似度, 通过多次尝试选出最优结果, 可控性不足, 尤其是在网络层数较大的情况下, 计算开销和存储开销很大. 因此, 本文提出加权跨层边聚类系数WCLECC, 解决层次数不可控的问题, 综合考虑层次数的所有可能值, 对于在所有层次数下取得的相似度值进行权重处理, 层次数越高权重越大, 对计算相似度的影响越大. 加权跨层边聚类系数WCLECC计算公式如下:
| $\begin{split} {{WCLECC}}(x,y) =& \frac{1}{{\textit{z}}}\sum\limits_{a = 1}^{|L|} {\frac{{2a}}{{\left| L \right|\left( {\left| L \right| + 1} \right)}}} \\ & \cdot \frac{{\left| {MN(x,a) \cap MN(y,a)} \right|}}{{\left| {(MN(x,a) \cup MN(y,a))/\left\{ {x,y} \right\}} \right|}} \end{split}$ | (1) |
其中, |L|为最大网络层数. MN(x,a)为x节点的多层邻居集合, 是指与节点x有a层或a层以上关联的邻居节点的集合, z为归一化因子. 以此做为衡量节点间紧密度的指标, 充分考虑了网络中不同层的稀疏程度, 且不需要进行参数的调整, 可以更准确的衡量节点间的关系强度.
|
图 6 ORCID异质网络中的元路径 |
| 表 1 ORCID网络元路径语义表 |
2.4 社区发现
通过使用WCLECC作为衡量节点间的相似度指标, 将多维网络转化为同质网络, 然后运用社区发现算法进行社区划分. 将节点i加入到节点j所在社区产生的模块度增量如式(2):
| $\begin{split} \Delta Q = &\left[ {\frac{{{\displaystyle\Sigma _{\rm in}} + {k_{i,in}}}}{{2m}} - {{\left( {\frac{{{\displaystyle\Sigma _{\rm tot}} + {k_i}}}{{2m}}} \right)}^2}} \right] \\ &- \left[ {\frac{{{\displaystyle\Sigma _{\rm in}}}}{{2m}} - {{\left( {\frac{{{\displaystyle\Sigma _{\rm tot}}}}{{2m}}} \right)}^2} - {{\left( {\frac{{{k_i}}}{{2m}}} \right)}^2}} \right] \end{split} $ | (2) |
∑in表示社区内边的权重之和, ∑tot表示与社区内节点相连的边的权重之和, ki,in表示社区内节点与节点i的边权重之和. 算法流程如下所示:
1)构建网络节点邻接矩阵A, 且将值均置为null;
2)遍历网络中的每一个节点x, 并记录该节点的所有邻居节点Y{y:y∈MN(x)};
3)计算每一对节点(x,y)的相似度WCLECC(x,y), 并更新邻接矩阵A(x,y)的值;
4)在邻接矩阵A中, 当A(x,y)!=null, 在新的网络中连接x节点与y节点并将WCLECC(x,y)作为边的权重, 重构研究者同质网络G′;
5)将G′中每个节点作为一个单独的社区, 社区数与节点数相同;
6)对G′每一个节点x, 依次将x加入其邻居所在社区之中, 计算加入前后的模块度变化情况ΔQ, 记录ΔQ最大的邻居节点n, 如果maxΔQ>0, 则把节点x加入到n所在社区, 否则不改变x所在社区;
7)重复步骤6), 直到所有节点所属社区不再变化;
8)对产生的社区进行压缩, 将每一个社区看作一个新的节点, 社区内边的权重之和当作社区自身环的权重, 社区间边的权重之和当作新节点之间边的权重;
9)重复步骤5), 直到全图模块度不再发生变化;
10)选出模块度最大时网络的社区划分结果, 即为最终社区划分情况.
3 实验与分析 3.1 社区评价标准常用的评价无监督社区划分结果优劣的指标为模块度(modularity)[21]. 其物理意义是社区内节点的连边数所占的比例与随机放置情况下社区内节点期望连边数的比例的差值, 定义如下:
| $Q = \frac{1}{{2m}}\sum\limits_{ij} {\left( {{A_{ij}} - \frac{{{k_i}{k_j}}}{{2m}}} \right)} \delta ({C_i},{C_j})$ | (3) |
| $\delta (u,v) = \left\{ \begin{array}{l} 1,\quad{\rm when}\quad{u = v} \\ 0,\quad{\rm else} \end{array} \right.$ | (4) |
其中, Aij是节点i和节点j之间边的权重, ki为所有与节点i相连的边的权重之和, Ci为节点i所属的社区, m为图中所有边的权重之和. 通常取值范围在[−1/2, 1]之间, 其值越靠近1, 表明网络划分结果越好.
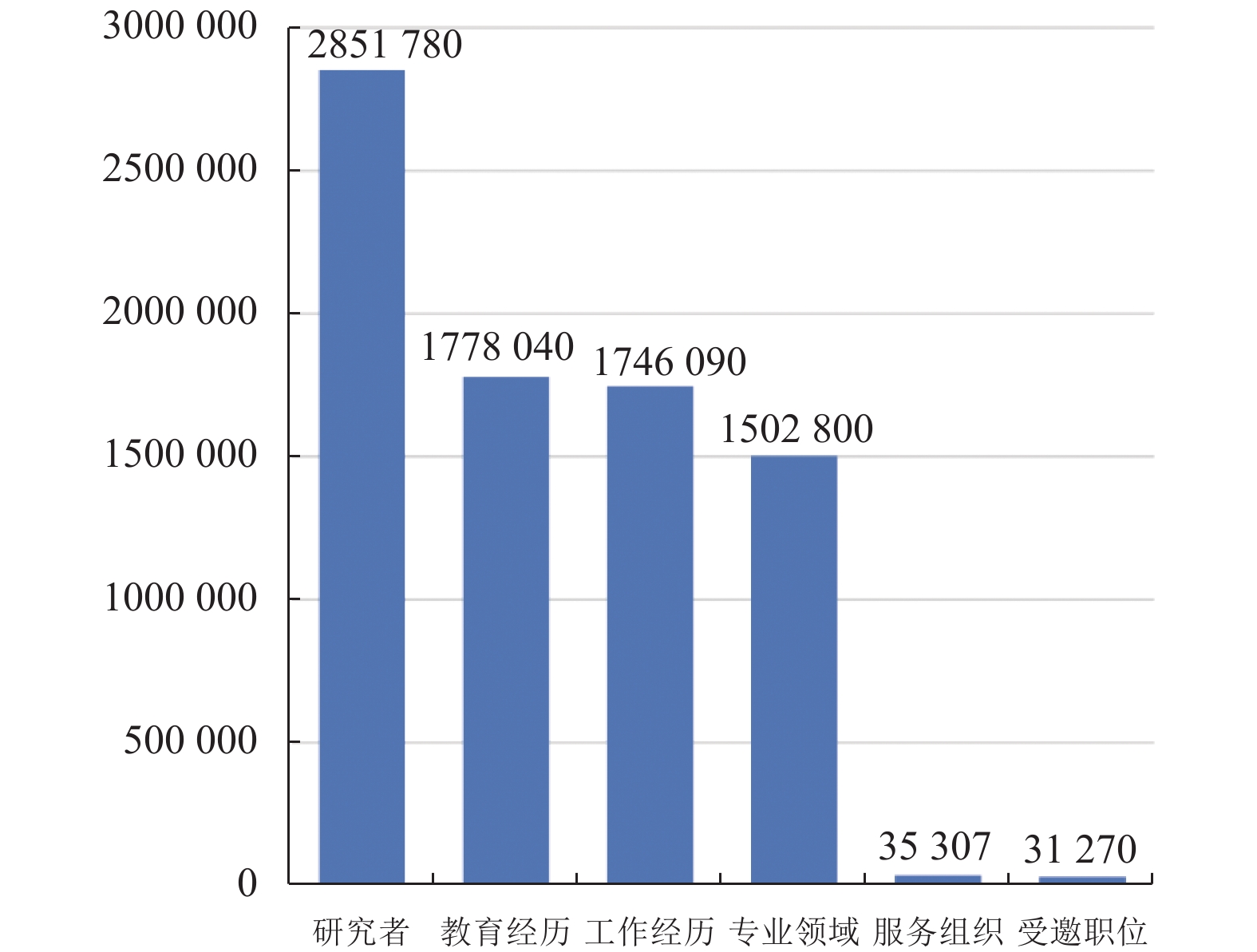
3.2 实验结果及分析 3.2.1 ORCID学术信息网络和研究者多维异质网络构建结果本文通过对ORCID数据集中研究者、教育经历、工作经历、受邀职位、服务单位的数据量进行统计, 如图7所示.
|
图 7 ORCID不同属性数据量统计 |
本文样本的选择根据ORCID标识符的11种尾号(0~9、X)分层选取, 每种尾号的数据选取1万条, 并去除掉未包含任何属性信息的数据, 共选取3组样本, 每组10万余名研究者的信息进行实验, 构建ORCID学术信息网络, 网络具体数据如表2和表3所示.
| 表 2 ORCID学术信息网络各节点数量统计 |
| 表 3 ORCID学术信息网络各属性边数量统计 |
在构建好的ORCID异质网络中, 通过表1中的元路径抽取研究者节点间不同属性的直接关联关系, 构建研究者多维异质网络, 网络中只含有研究者节点及不同属性连边, 网络具体数据如表4所示.
通过元路径的抽取, 可以将ORCID异质网络中多种类多属性的节点和边简化为只存在研究者节点及其之间多属性边的多维网络, 减少了网络节点类型, 避免了其余组织机构节点对社区划分产生的影响, 降低了网络的复杂性和计算的复杂性.
| 表 4 研究者多维异质网络连边数量统计 |
3.2.2 社区划分结果
(1) 通过构建人造稀疏网络和稠密网络对本文算法进行实验, 测试WCLECC与CLECC在取不同a值的情况下对网络的划分取得的效果, 以此检测是否通过WCLECC避免了CLECC参数的不确定性对实验产生的影响且能取得优于CLECC的实验结果.
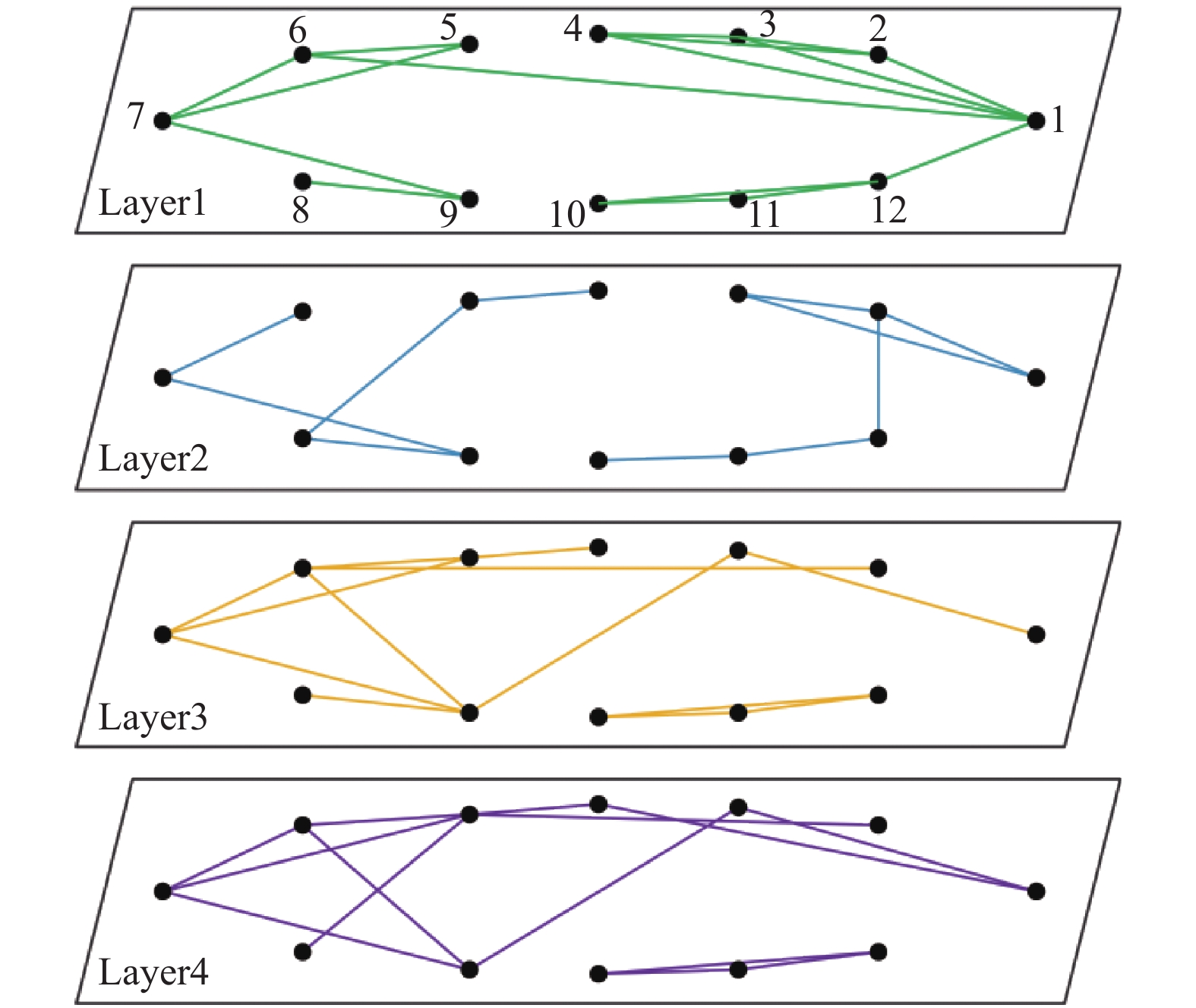
① 图8为4层稀疏网络中每层的初始连边情况.
|
图 8 稀疏网络各层初始情况 |
实验结果如表5所示, 可以看出使用CLECC在a=2时, 网络划分可以取得最大模块度Q, 而使用WCLECC划分的社区数量和成员与其相同且模块度提高了1.85%, 实验效果更好.
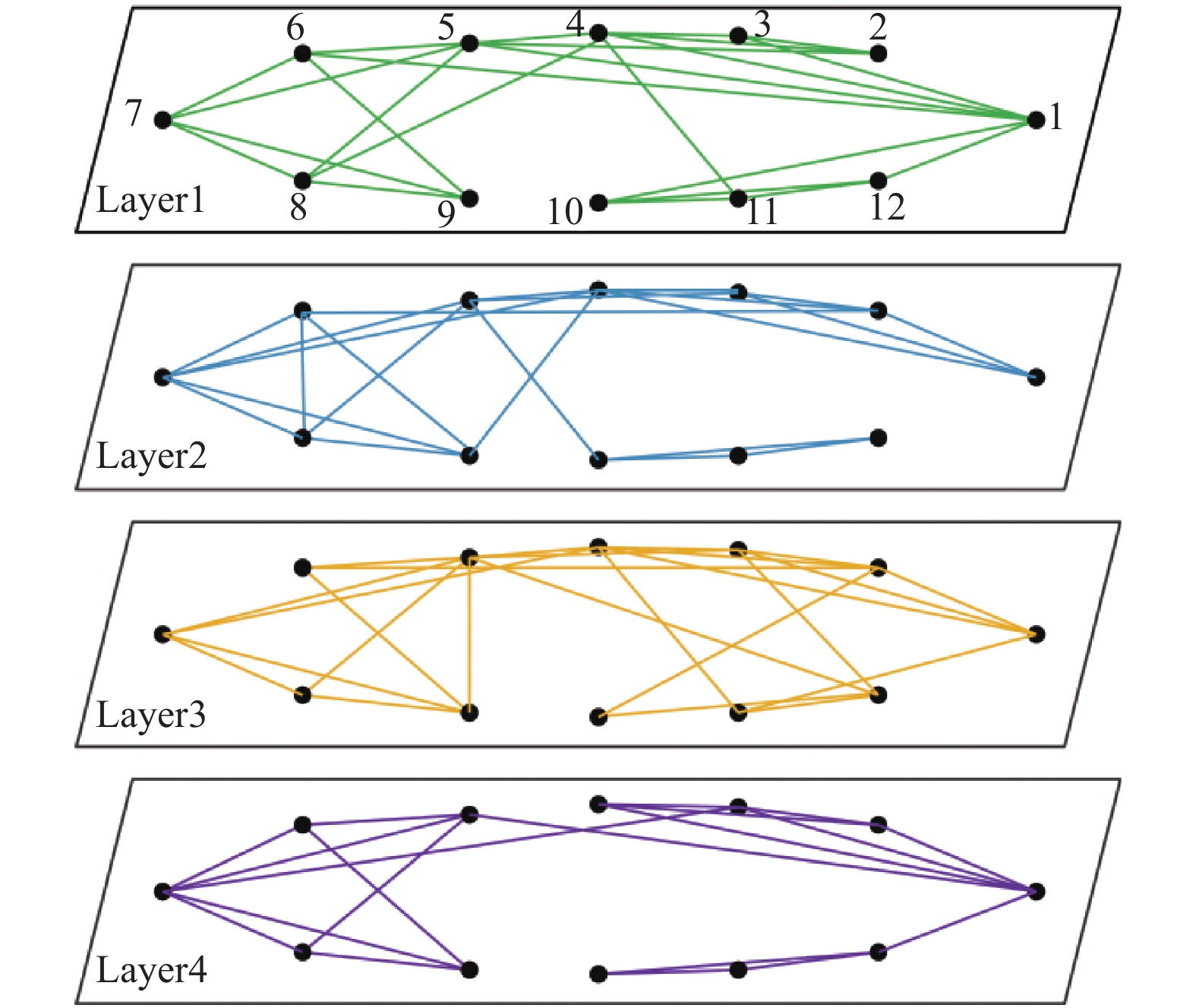
② 图9为4层稠密网络中每层的初始连边情况.
实验结果如表6所示, 可以看出使用CLECC在a=3时, 网络划分可以取得最大模块度Q, 而使用WCLECC划分的社区数量和成员与其相同且模块度提高了1.65%, 实验效果更好.
通过上述实验可知, 使用CLECC进行社区划分时, 在稀疏网络中a取较小值可以得到更优的实验结果, 在稠密网络中a取较大值可以得到更优的实验结果. 究其原因, 当网络稀疏时, 高层次邻居节点远少于低层次邻居节点, 当a取较大值时会造成部分节点间相似度丢失, 影响社区划分的准确性, a取较小值时会有更多的邻居节点参与相似度的计算, 提高计算准确性. 而当网络稠密时, 高层次邻居节点与低层次邻居节点数量相近, a取较大值能更准确计算出节点间的相似度, 使网络划分更准确. 针对稀疏程度不确定的网络, 使用CLECC进行社区划分必须要依次尝试a取值的所有可能值才能找到最优的实验结果, 而WCLECC针对CLECC参数不确定的问题, 综合考虑了a参数的所有可能取值, 简化了参数选择的过程, 并且在取得相同划分结果的同时能取得更优的实验结果. 因此, 当网络稀疏程度明确时, 可以考虑使用CLECC进行计算, 也可以使用WCLECC进行计算, 当网络稀疏程度不明确时, 为避免多次尝试不同参数可以使用WCLECC进行计算从而进行社区划分.
| 表 5 稀疏网络社区划分结果表 |
同时, WCLECC对于CLECC的改进主要在于参数选择的优化, 针对稀疏程度不明的网络可以减少对不同参数的尝试并能得到更优的结果, 但WCLECC需要同时考虑各个层次的邻居, 增加了部分计算时间, 但整体时间仍保持在同样的量级, 对时间开销方面并未造成过大的影响.
|
图 9 稠密网络各层初始情况 |
| 表 6 稠密网络社区划分结果表 |
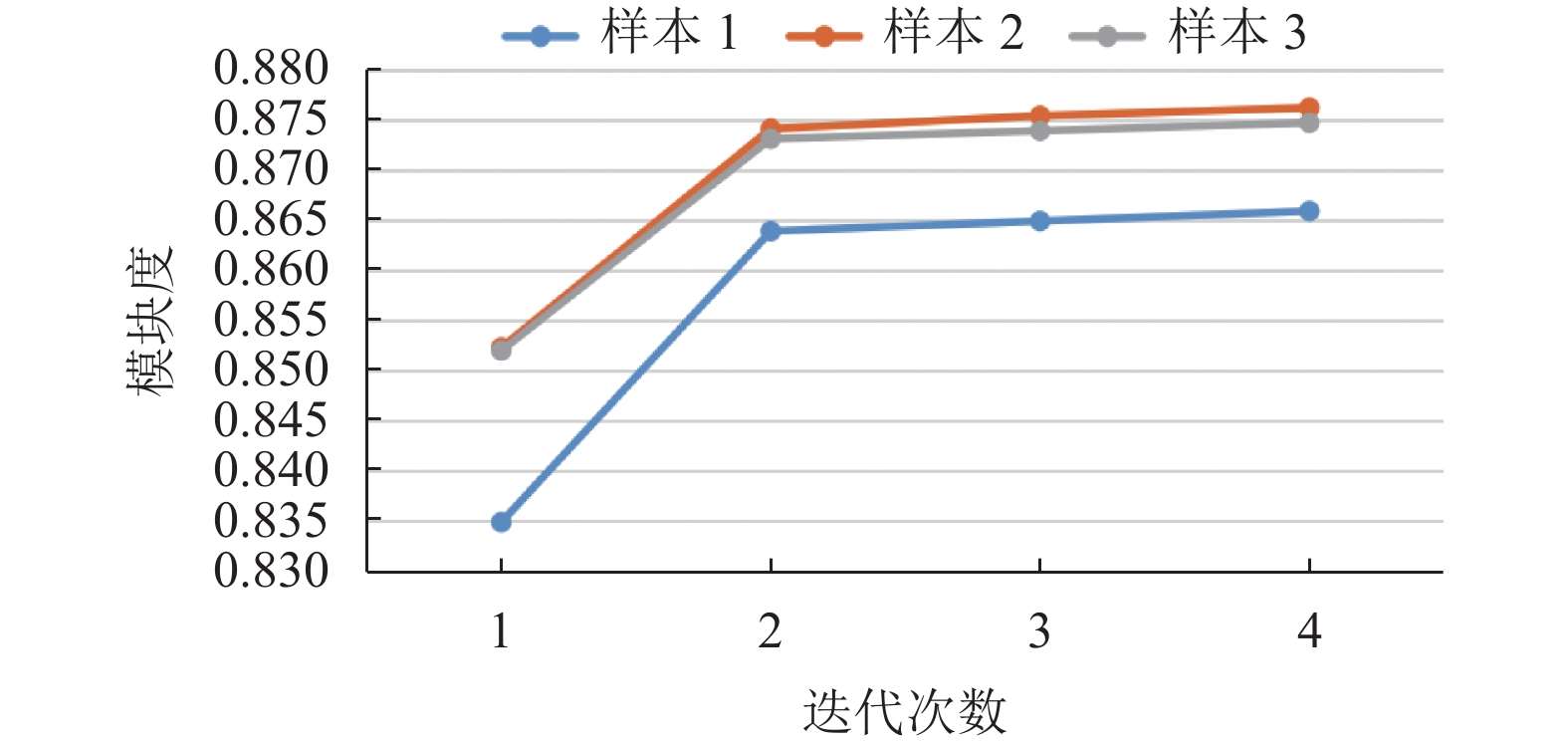
(2) 在构建好的研究者多维异质网络中运行本文算法进行社区发现. 图10为3次实验过程中社区划分中模块度随迭代次数的变化, 选取模块度最高时的划分结果作为最终的实验结果. 表7为3次实验中划分的社团数和模块度结果的对比.
由上述结果可以看到,
|
图 10 社区划分中模块度随迭代次数的变化 |
| 表 7 社区划分结果 |

|
图 11 孤立节点占比情况 |
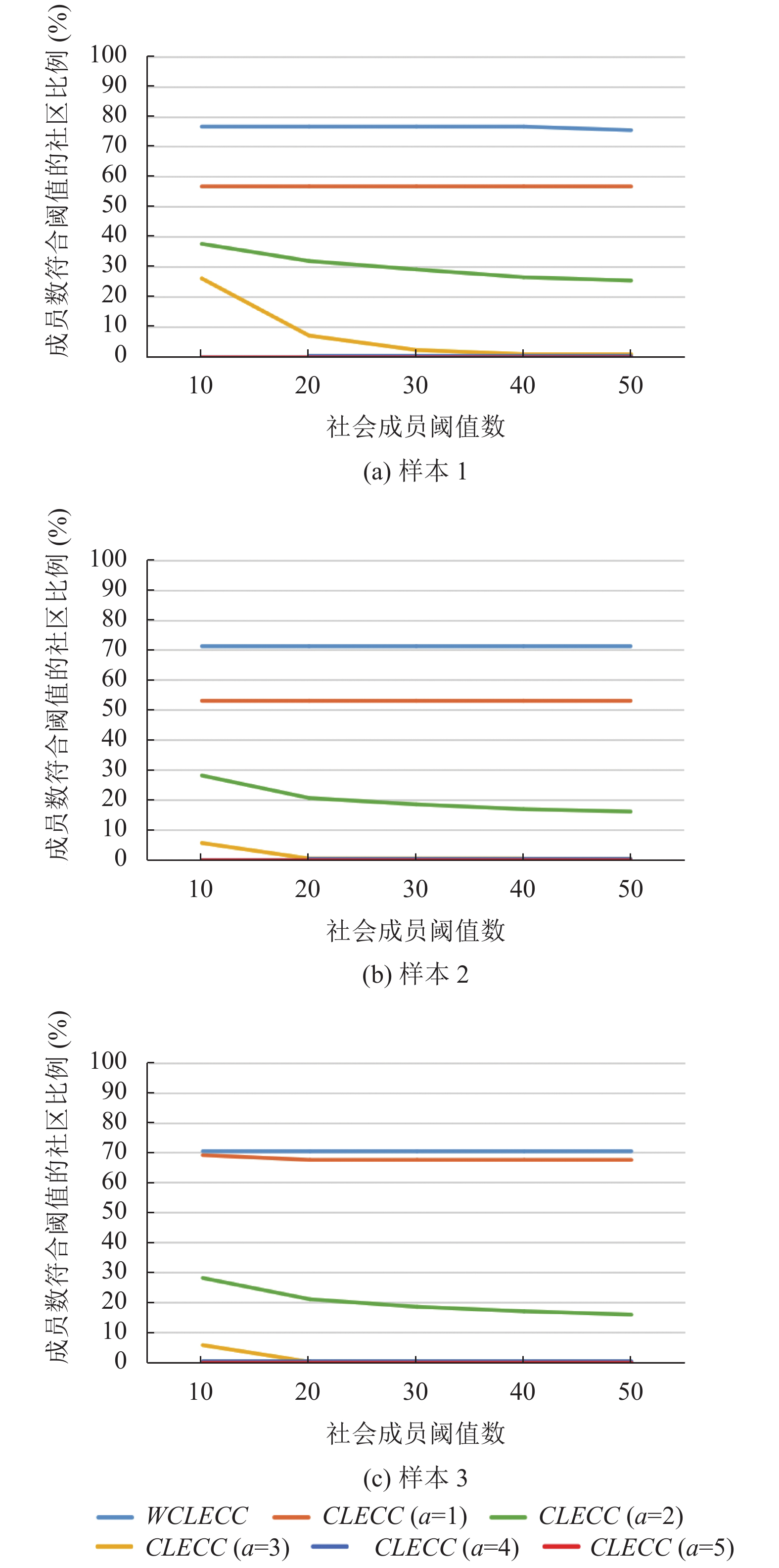
图12展示了3次实验中社区成员数超过不同阈值的社区占比情况.
通过观察上述结果, 当a=1时, 实验结果中模块度的值最低, 划分社区数最少, 虽然所划分的社区能覆盖最多的节点, 但整体来看划分效果不佳; 当a=2时, 能取得较好的模块度结果及适中的社区数, 孤立节点占比较低, 虽然成员数超过不同阈值的社区数量较少, 产生了大量的小社区团体, 但整体来看取得了较好的实验结果; 当a>2时, 虽然模块度的值均能接近理论最优值, 但划分的社区数量过多,a=3时, 孤立节点占比超过50%, 且社区成员超过10人的社区比例仅在样本1中达到20%以上, 其余均低于10%, 当a>3时, 所划分社区几乎全是孤立节点社区, 未起到社区划分的真正意义, 实验结果不佳. 究其原因, 由于不同层次的网络稀疏程度不同, 当层数越深, 节点间有多层关联的邻居越少, 仅有少量节点间拥有多层次的关联关系, 忽略了低层次关联产生的影响.WCLECC很好的解决了这一问题, 充分考虑了所有层的关联关系, 模块度的值和孤立节点的占比情况均优于a=2的结果, 在成员数符合阈值的社区比例中也能取得最优的结果, 可见使用WCLECC减少了孤立节点和小成员数社区的产生, 整体来看取得的效果最佳.
|
图 12 成员数符合阈值的社区占比情况 |
综上所述, 通过使用研究者学术活动信息构建ORCID异质网络, 并使用WCLECC能取得最优的社区划分结果, 既充分考虑了研究者节点间的多层关联关系, 又避免了参数的不可控, 同时产生的社区覆盖了较多的研究者节点, 减少了孤立节点的出现, 也减少了小成员数社区的出现, 划分出了高质量的社区, 得到了较好的实验结果.
4 结语本文通过对ORCID数据进行分析, 使用研究者学术活动构建科研信息网络进行学术社区的发现, 通过元路径抽取出研究者节点间的直接关联关系, 降低了异质网络的复杂度, 避免了中间节点对社区划分产生的影响, 提出加权跨层边聚类系数解决了多层网络中节点相似度的度量问题, 改善了跨层边聚类系数的参数不可控性, 充分利用研究者的学术信息去寻找其学术团体, 对学术社区发现提出了一种新的思路. 在人造网络和真实数据集上进行实验, 均取得了较好的实验结果. 同时, 本文还存在一定的问题, 如尚未对全部数据进行实验, 不同属性信息对划分结果的影响等也值得更进一步的考虑, 后续的工作将针对这些问题进行进一步的研究.
| [1] |
郑琳. 面向机构的科研人员唯一标识符应用与发展研究. 图书与情报, 2018(1): 134-140. DOI:10.11968/tsyqb.1003-6938.2018017 |
| [2] |
Researcher ID. http://www.researcherid.com/#rid-for-researchers.
|
| [3] |
Adamich T. Linked data identifiers: Part 1–International Standard Name Identifier (ISNI). Technicalities, 2014, 34(1). |
| [4] |
刘润达, 王运红. 开放研究人员及贡献者唯一标识(ORCID)概述. 情报科学, 2013, 31(11): 86-90. DOI:10.13833/j.cnki.is.2013.11.027 |
| [5] |
Akers KG, Sarkozy A, Wu W, et al. ORCID author identifiers: A primer for librarians. Medical Reference Services Quarterly, 2016, 35(2): 135-144. DOI:10.1080/02763869.2016.1152139 |
| [6] |
赵卫绩, 张凤斌, 刘井莲. 复杂网络社区发现研究进展. 计算机科学, 2020, 47(2): 10-20. DOI:10.11896/jsjkx.190100214 |
| [7] |
周园春, 王卫军, 乔子越, 等. 科技大数据知识图谱构建方法及应用研究综述. 中国科学: 信息科学, 2020, 50(7): 957-987. DOI:10.1360/SSI-2019-0271 |
| [8] |
黄国彬, 郑琳. 科研人员唯一标识符的组成与应用研究. 图书情报工作, 2015, 59(4): 25-31. DOI:10.13266/j.issn.0252-3116.2015.04.004 |
| [9] |
Aerts R. Digital identifiers could keep up with authors' moves. Nature, 2008, 454(7204): 575. DOI:10.1038/454575c |
| [10] |
周园春, 常青玲, 杜一. SKS: 一种科技领域大数据知识图谱平台. 数据与计算发展前沿, 2019, 1(1): 82-93. DOI:10.11871/jfdc.issn.2096-742X.2019.01.009 |
| [11] |
Sun YZ, Yu YT, Han JW. Ranking-based clustering of heterogeneous information networks with star network schema. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France. 2009. 797–806.
|
| [12] |
Sun YZ, Norick B, Han JW, et al. PathSelClus: Integrating meta-path selection with user-guided object clustering in heterogeneous information networks. ACM Transactions on Knowledge Discovery from Data, 2013, 7(3): 11. DOI:10.1145/2500492 |
| [13] |
Lu ML, Qu ZH, Wang ZH, et al. Hete_MESE: Multi-dimensional community detection algorithm based on multiplex network extraction and seed expansion for heterogeneous information networks. IEEE Access, 2018, 6: 73965-73983. DOI:10.1109/ACCESS.2018.2883638 |
| [14] |
谷瑞军, 陈圣磊, 陈耿, 等. 复杂合著网络中的重叠社团发现与可视化. 图书情报工作, 2012, 56(12): 72-76, 59. |
| [15] |
逯万辉, 谭宗颖. 基于显性-隐性二元关系的学术社区发现方法研究. 情报科学, 2018, 36(1): 130-134. DOI:10.13833/j.issn.1007-7634.2018.01.023 |
| [16] |
Amelio A, Pizzuti C. Community detection in multidimensional networks. 2014 IEEE 26th International Conference on Tools with Artificial Intelligence. Limassol, Cyprus. 2014. 352–359.
|
| [17] |
Kanawati R. Community detection in social networks: The power of ensemble methods. 2014 International Conference on Data Science and Advanced Analytics. Shanghai, China. 2014. 46–52.
|
| [18] |
Zhang JY, Yang XP, Wang L. Clustering via meta-path embedding for heterogeneous information networks. 2020 IEEE International Conference on Knowledge Graph. Nanjing, China. 2020. 188–194.
|
| [19] |
Paul S, Chen YG. Spectral and matrix factorization methods for consistent community detection in multi-layer networks. The Annals of Statistics, 2020, 48(1): 230-250. |
| [20] |
Bródka P, Filipowski T, Kazienko P. An introduction to community detection in multi-layered social network. Proceedings of the 4th International Conference on Information Systems, E-Learning, and Knowledge Management Research. Mykonos, Greece. 2013.185–190.
|
| [21] |
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69(2): 026113. DOI:10.1103/physreve.69.026113 |
 2021, Vol. 30
2021, Vol. 30



