海底面积广阔, 蕴藏着人类赖以生存的丰富资源, 但由于深海环境复杂, 人类技术条件有限, 迄今为止都未能窥探海底全貌. 海水具有光线难以穿透的性质, 从海面上无法准确的掌握海底情况. 相比较于其他技术而言, 视觉技术可以很直观的获取深海信息, 已经成为深海研究的重要手段. 单幅图像视野小, 为了更清晰的得到海底全景图, 需要拼接海底图像. 图像配准是图像拼接的第一步, 也是最核心的一步. 图像配准的准确度直接影响图像拼接的最后结果.

图像配准的目的是将两张具有重叠部分的邻接图像进行空间匹配对准. 目前, 国内外针对图像配准的研究做了很多的工作. 常见的配准方法可以分为两大类: (1)基于灰度的图像匹配^[1-4]: 这种方法直接利用图像的灰度信息完成匹配运算, 主要依赖于像素值, 对噪声比较敏感, 容易受灰度, 尺度和尺寸变化的影响. 使用该类算法要求两张图像之间重叠面积大, 几何变形小. 该类算法要求两幅图像重叠面积大, 而机器人拍摄海底图像重叠面积小, 此类基于灰度的图像配准在机器人自主拍摄的海底图像中不具有可行性. (2)基于特征的图像配准^[5-11]: 这种算法不直接依赖于像素值, 需要在图像中提取对缩放, 旋转, 灰度变换具有不变性的特征. SIFT^[12,13]、SURF^[14,15]和DAISY^[16]是检测和描述在水外环境中捕获的物体特征的著名技术. 这些标准描述符已被证明对几何变化最为稳健. 这些算法对图像的噪声, 旋转, 缩放和光照等变化不敏感. 海底图像不同于一般的地面图像. 由于光的衰减作用, 越到海底深处, 光照强度越低; 深海悬浮物的散射以及人造光源的影响, 造成海底图像亮度不均匀, 中间区域亮, 两边区域暗, 对比度低, 质量退化. 同时, 机器人拍摄过程中, 海底地面凹凸不平. 相邻两张图像拍摄角度会发生一定的偏差, 图像之间的几何变形大, 重叠面积不超过35%. 基于特征的图像配准, 可以适当的减少缩放, 旋转, 灰度等变换的影响. 由于深海图像质量下降, 直接的使用传统特征点配准算法提取到的特征点数量少, 描述子辨别能力低; 最后所得配准对应点错误率高, 部分图像甚至找不到正确的对应点. 基于运动一致性的GMS^[17]特征点配准算法以划分网格的方式进行精匹配. 对应点集中于一个区域, 容易出现一个区域均为错误对应点的情况. 2012年, Prabhakar等^[18]根据整个水下图像序列场景块的纹理参数和颜色不变性, 提出了适用于水下环境的局部特征描述符LBP-SURF. LBP-SURF描述子, 它可以有效地提取水下图像的纹理特征. 该算法主要是在SURF的基础上加入了LBP, 使描述子具有灰度不变性. 这种方法要求两张图像相似区域变化小. 但机器人拍摄海底图像, 人造光源使两张图像相似区域变化明显, 不同图像的相似区域特征点由LBP-SURF计算的描述子差别大, 特征点匹配错误率高. 该方法不适用于机器人拍摄的海底图像. 2017年, Raut等^[19]针对水下图像运用基于改进的SIFT算法提取特征点, 采用Gabor滤波器作为前置滤波器, 利用Hausdorff距离计算关键点之间的距离. 2010年, 谢雨来等^[20]就SURF在深海图像上的应用做了研究, 用SURF算法获取参考图像和配准图像的特征点. 2014年, 李超^[21]发表了将SURF算法运用到海底图像. 2016年, 贺磊盈等^[22]对有序列的深海图像做了研究, 提出了一种基于卡尔曼滤波跟踪序列图像的空间位置实施序列图像的快速匹配方法. 这些方法主要针对的是一般的深海图像, 对于本次实验机器人拍摄的海底图像中不具有可行性.

综上所述, 针对机器人拍摄的序列海底图像, 本文提出了先将海底图像进行适当的预处理, 改善图像质量; 根据机器人拍摄图像的航行特点, 在基于图像信息的配准算法基础上加入导航先验信息. 利用导航数据, 缩小特征点配准区域, 从而有效的增加图像配准对应点.

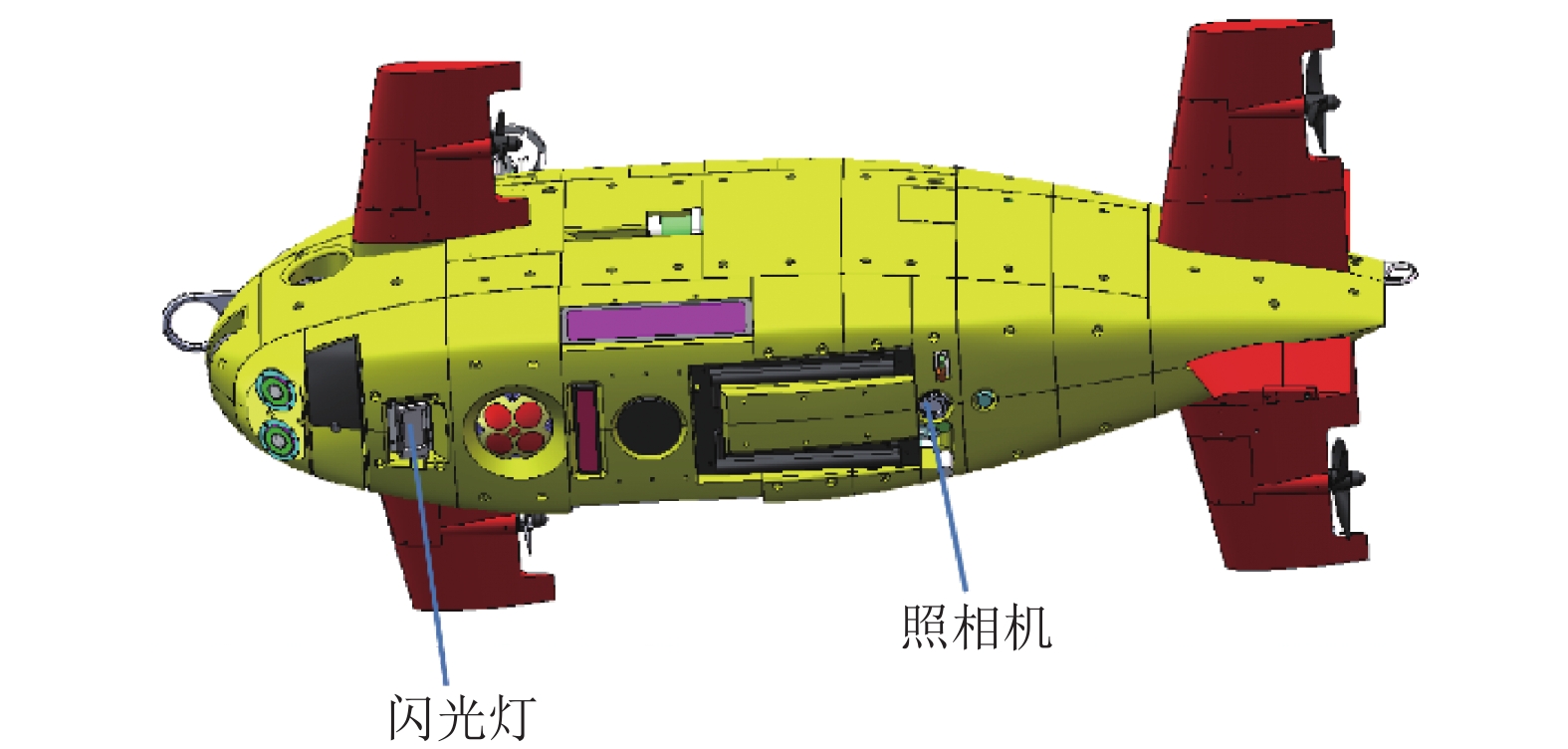
1 水下机器人航行特点

海底图像由水下机器人根据特定航线拍摄. 机器人图像如图1所示, 从图中照相机的位置可知, 机器人向下拍摄图像.

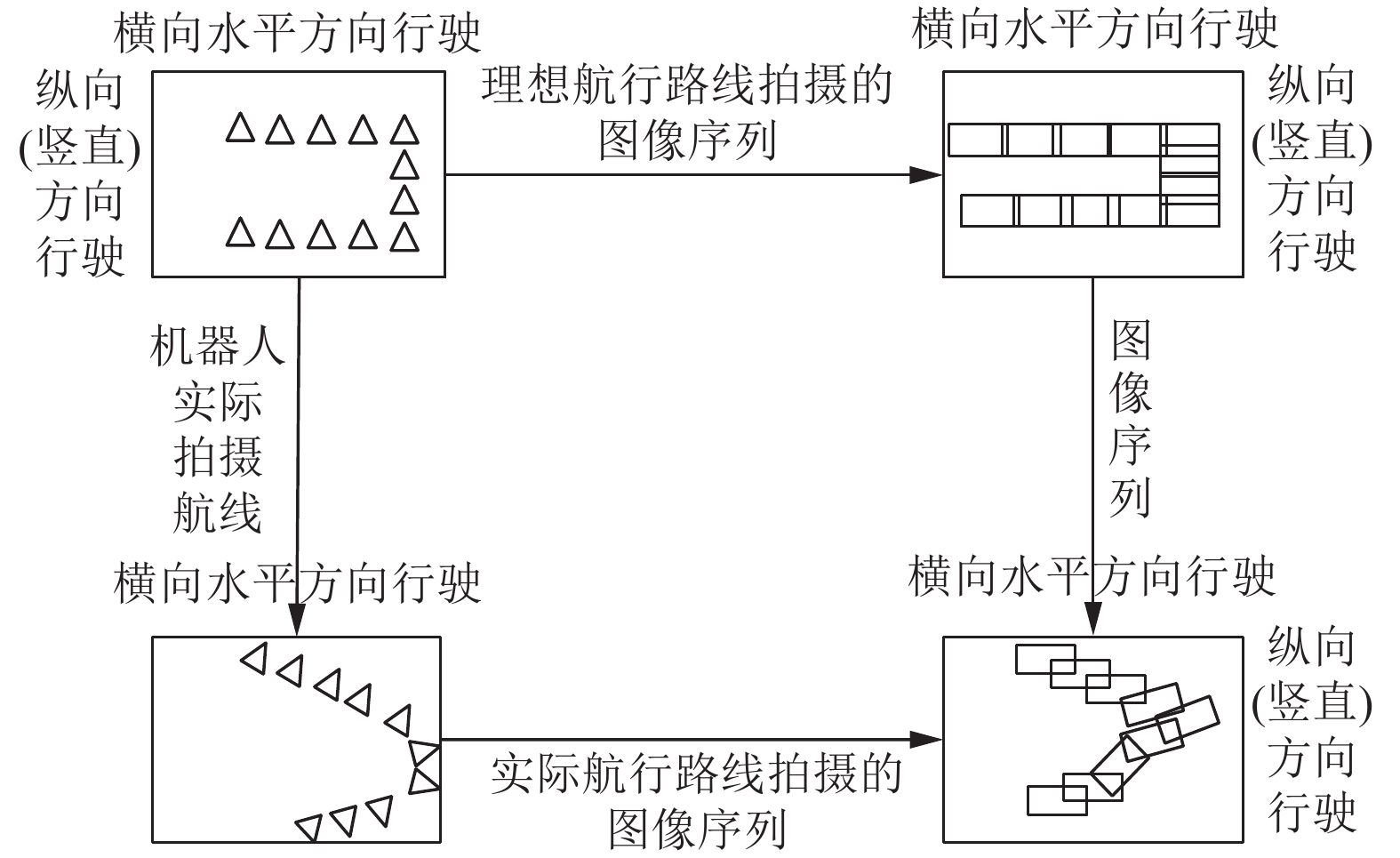
每台机器人配有传感器和闪光灯, 海底拍摄需要打开闪光灯, 拍摄图像的同时记录拍摄位置的横纵坐标. 如图2左上角第一张图所示: 方框表示机器人拍摄范围. 三角形代表机器人拍摄图像所在位置. 理想情况下的机器人拍摄航线严格按照水平方向和竖直方向, 拍摄的图像序列如右上角第二张图所示(每一个长方形表示一张图像): 相邻两张图像相似区域位于一条水平线上. 实际情况中, 海底地面凹凸不平, 机器人拍摄航线会出现一定的偏差. 如左下角第3张图所示: 水平方向(横向)会有一定的倾斜, 竖直方向出现旋转角度. 实际所拍摄的图像序列如右下角第4张图所示: 邻接图像的相似区域并不严格处于水平线范围内, 竖直方向拍摄的图像存在一定的旋转角度.

2 图像预处理

由于光的衰减, 水中悬浮颗粒散射和人造光源的影响, 海底图像具有对比度低, 中间区域亮, 两边区域暗的特点. 因此, 本文针对海底图像质量差的问题, 对原始图像进行预处理. 预处理步骤如下:

(1)光照补偿: 即从数据集中选取10张低纹理图像, 灰度值化, 对所选10张图像进行像素平均. 公式为:

$ F(x,y)=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}{M}_{i}(x,y)} $

(1)

通过高斯滤波器获得光照补偿因子 $F(x,y)$ ; 对海底图像 $M(x,y)$ 光照补偿得到图像 $Z(x,y)$ . 光照补偿公式如式(2)所示:

$ Z(x,y) = \frac{{M(x,y)}}{{F(x,y)}} $

(2)

(2)对图像灰度值范围进行线性调整. 原图像 $Z(x,y)$ 的灰度范围是 $\left[ {m,M} \right]$ , 调整后的图 $G(x,y)$ 的灰度范围是 $\left[ {n,N} \right]$ , 变换公式为:

$ G(x,y) = \frac{{N - n}}{{M - m}}\left[ {Z(x,y) - m} \right] + n $

(3)

3 基于先验信息的带状区域计算

为减小描述子辨别能力低对图像配准的影响, 根据导航信息计算拍摄相邻两张图像的物理偏移量, 通过物理偏移量估算源图像特征点对应目标图像的匹配区域(即带状区域). 如图3所示, 取源图像方框内的特征点, 经过相对应模型计算确定在目标图像中的方框区域(即带状区域)内寻找最匹配的特征点. 以带状区域配准^[23]代替全局配准, 提高了特征对应点数目和准确率.

3.1 水平航线带状区域计算模型

建立水平航线数学模型计算邻接图像配准区域. 机器人左右移动拍摄图像, 由于海底凹凸不平, 机器人左右(横向)移动的同时伴随则上下(纵向)移动. 相邻两幅图像对应点不严格处于一条水平线范围内. 利用导航数据得出拍相邻两幅图像的左右物理偏移量与对应的像素偏移量, 求得每两个像素点代表的物理距离; 根据导航信息的上下物理偏移量得出纵向像素点偏移量, 计算特征对应点配准区域(即带状区域), 在配准区域内进行特征对应点匹配. 计算公式定义为:

$D = {y_i} + \frac{I}{X}Y \pm \sigma $

(4)

其中, X表示计算得到的两幅图像之间左右物理位置偏移量, 求得两张图像物理偏移量对应的像素值I, Y表示两张图像之间纵向物理位置偏移量, 通过 $\dfrac{I}{X}Y$ 计算纵向像素偏移值, 使用模板图像特征点纵坐标 ${y_i}$ 加上 $\dfrac{I}{X}Y$ 与 $\sigma $ 的误差量, 确定配准区域D, 作为模板图像特征点在待配准图像的配准区域, 缩小配准区域, 增加对应点正确率.

3.2 旋转航线带状区域计算模型

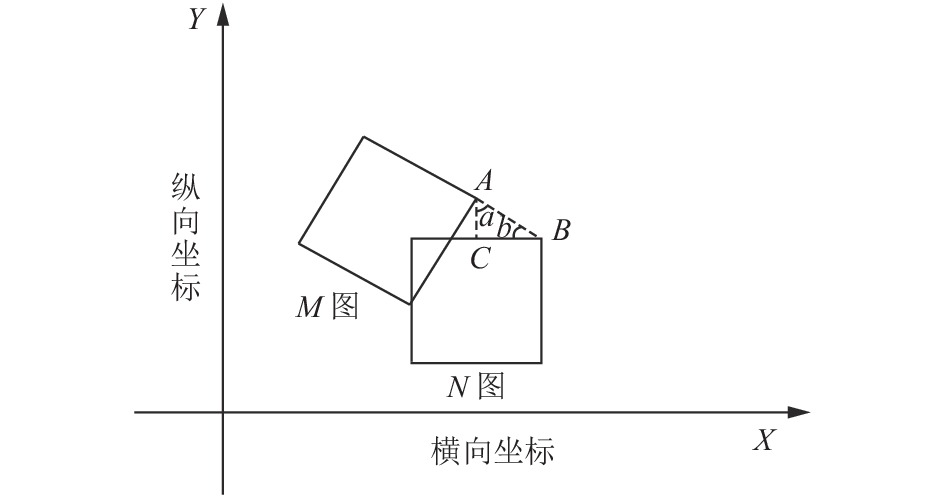
邻接旋转航线图像的配准区域数学模型计算: 机器人旋转拍摄图像, 首先根据导航物理位置信息计算相邻两幅图像旋转角度. 取机器人拍摄图像的物理位置坐标为图4中的A, B两点(A, B两点可以由图中任意两个相对位置取代). 横向坐标表示物理平行方向位置坐标, 纵向坐标表示物理竖直方向位置坐标. 将图N旋转角度b与图M平行. 然后计算图N中特征点对应图M中的带状区域. 计算方法如下:

角度计算公式如式(2):

$\theta = \arctan \frac{{{x_2} - {x_1}}}{{{y_2} - {y_1}}}$

(5)

其中, ${x_2} - {x_1}$ 是A, B两点的横向坐标差值(即BC线段的长度), ${y_2} - {y_1}$ 是A, B两点的纵向坐标差值(即AC的长度). 利用式(2)求出图4中的角a (即公式中的 $\theta $ ). 角a与角b的和为90度, 所以旋转角度 $b = 90 - a$ , 则可以得出 $\cos (b) = \cos (90 - a) = \sin (a)$ . 带状区域计算公式如式(3)所示:

$D = {y_i} + \frac{I}{X}\cdot\frac{Y}{{\sin \theta }} \pm \sigma $

(6)

其中, D表示两张邻接旋转图像相似区域像素偏移量(即带状配准区域). X表示计算得到的两幅图像之间横向物理位置偏移量, 求得两张图像物理偏移量对应的像素值I . Y表示拍摄两幅图像机器人的纵向位置偏移量. $\dfrac{Y}{{\sin \theta }}$ 求出两幅图像平行时的位置偏移量. 通过 $\dfrac{I}{X}\cdot\dfrac{Y}{{\sin \theta }}$ 得到模板图像特征点对应于待配准图像的偏移像素量, 特征点纵坐标 ${y_i}$ 加上 $\dfrac{I}{X}\cdot\dfrac{Y}{{\sin \theta }}$ 与 $\sigma $ 的误差量得出配准区域, 缩小配准区域, 有效的提高特征对应点的正确率.

4 实验过程 4.1 实验总流程图

本文实验总流程如图5所示. 实验中采用了具有重复纹理和低纹理的海底图像. 分别由平移航线和旋转航线所拍摄. 先将所选图像采用2的方法进行预处理, 以缓解海底图像对比度低, 光照不均匀的情况. SIFT是图像的局部特征提取算法, 其对旋转、尺度缩放、亮度变化保持不变性, 对视角变化、仿射变换、噪声也保持一定程度的稳定性. 对存在旋转, 缩放, 尺度变化的海底图像具有很高的适用性. 采用基于SIFT算法提取特征点, 在KNN (K=1)算法的基础上加入先验信息进行特征点匹配, 最后通过RANSAC和最小二乘法筛选内点. 得到特征对应点正确率高的图像配准.

4.2 实验数据

本文实验数据由水下机器人拍摄于2019年4月中国南海5000米以下的深海海域. 拍摄范围约300×300平方米, 机器人航线分为东西走向, 边缘航线需要经过旋转拍摄. 相邻两张图像的横向物理位移大致为2米, 纵向偏移量不等, 每张图像覆盖面积2×2米, 拍摄内容存在重复纹理和低纹理的问题.

图6所示机器人实际拍摄海底图像的航线, 根据机器人记录的坐标信息所绘制, 图中数字表示由左行驶到右一次的拍摄.

表1是机器人从左到右水平方向行驶拍摄所记录的横向和纵向坐标信息. 表2是机器人旋转(转换行驶方向)行驶拍摄所记录的横向和纵向坐标信息.

4.3 图像预处理

深海图像本文方法预处理对比如图7所示: 预处理之前如图7(a)所示, 可以明显的看出图像光照不均匀, 中间区域偏亮, 两边区域偏暗, 暗处图像对比度低. 经过调整光照, 增强等预处理后如图7(b)所示: 图像特征明显, 减少了图像明暗不一的情况.

4.4 加入先验信息具体实验步骤

(1)实验基于SIFT算法对图像进行特征点提取.

(2)计算带状配准区域D.

① 平移航线图像的带状区域计算: 利用表1相邻两行横向坐标计算机器人水平方向移动距离X; 论文中所选图像像素为640×480, 拍摄邻接图像横向物理距离对应的图像像素为一张图像的像素大小减去邻接图像相似区域的像素值; 本次实验数据相邻图像之间的相似区域不超过35%, 甚至更小, 所以大致的估算像素偏移量为图像的宽, 即I=480. 相邻两行纵向坐标的差Y; 经过观察及实验得出, 机器人纵向差值小于1米, 偏差角度小于10度, $\sigma $ 取值100即不会使配准区域过大, 也不会小于重叠面积. 即:

$ D = {y_i} + \frac{I}{X}\cdot\frac{Y}{{\sin \theta }} \pm 100 $

(7)

② 旋转航线的带状区域计算: 根据表2相邻两行横向坐标的差值 ${x_2} - {x_1}$ 与纵向坐标的差值 ${y_2} - {y_1}$ 通过 $\theta = \arctan \dfrac{{{x_2} - {x_1}}}{{{y_2} - {y_1}}}$ 计算旋转角度 $\theta $ ; $\dfrac{I}{X}\cdot\dfrac{Y}{{\sin \theta }}$ 计算相邻两张旋转图像之间的像素偏移量, ${y_i}$ 为特征点纵坐标, 通过观察及实验得出, 机器人旋转角度小于20度, $\sigma $ 取60. 即:

$ D = {y_i} + \frac{I}{X}\cdot\frac{Y}{{\sin \theta }} \pm 60 $

(8)

(3)取图像A中的某个关键点, 在图像B的带状区域(由第(2)步求出)寻找最合适的特征对应点, 采用最近邻(KNN, K=1)匹配特征点, 进行初始匹配. 遍历A中的所有关键点, 在对应带状区域找出所有匹配点.

(4)本次实验数据中80%的图像之间的变换仅包含简单的平移和旋转, 部分存在缩放, 所以选择相似变换模型, RANSAC和最小二乘法求取变换关系(阈值设置为4.5), 筛选初始匹配对应点, 保留内点.

5 实验结果和分析

实验分为两大类: (1)预处理前后初始匹配实验结果对比. (2)预处理的情况下未加入带状区域的特征点配准和加入带状区域的配准实验对比. 这两类都可以通过比较正确匹配点个数判断方法的有效性. 其中, 第(2)类实验又分为平移航线和旋转航线两种不同的情况. 平移航线选取存在重复纹理问题的图像, 旋转航线选取存在低纹理问题的图像.

5.1 第1类实验结果对比

预处理实验共选取500张深海海底图像, 经计算, 其中80%的图像配准点个数提高了25%. 图8为部分实验图.

如图8, 表3所示为第1类实验结果. 经过本文方法预处理后的图像在亮度, 对比度方面改善明显. 从实验结果可以分析得出, 由于预处理前的图像对比度低, 图像模糊, 光照不均匀, 中间区域亮, 两边区域较暗; 提取到的初始匹配特征点数量少, 且正确的匹配对应点少, 无法满足求取变换矩阵的最低对应点数目. 预处理后的图像光照均匀, 有效的改善了图像亮度, 对比度增强, 提取到较多的特征点, 初始匹配对应点得到了增加, 可以求得较精确的变换矩阵.

5.2 第2类实验结果对比

加入带状信息的实验选取500张深海海底图像. 整体图像配准点正确率提高了20%. 图9, 图10所示为本部分实验效果图.

如图9, 表4所示为第2类情况中的平移航线未加入导航信息与加入导航信息的实验对比. 图10, 表5所示为第2类情况中的旋转航线未加入导航信息与加入导航信息的实验对比. 由实验结果可以分析得出, 相邻两张图像重叠区域不足图像的35%, 且图像存在严重的重复纹理和低纹理问题, 导致描述子辨别能力降低. 经过RANSAC和最小二乘化筛选内点之后仅得到不足5对匹配对应点, 所求出的变换矩阵精确度低. 按照本文方法, 加入先验信息作为引导思想, 缩小特征点匹配面积, 减少其他区域描述子的干扰, 从而有效的增加了匹配对应点的数目.

实验结果表明, 文中提出的基于先验知识和图像信息的方法, 可以有效的解决描述子辨别能力降低的问题, 提高特征对应点的数目和正确率. 在重复纹理和低纹理的情况下, 不同区域的特征描述子之间的相似度极高, 在全局特征点配准干扰性大, 更增加了配准的难度. 采用本文方法, 缩小配准区域, 带状区域配准代替全局配准. 减少了错误特征点的干扰, 降低了误匹配的概率, 得到满意的配准结果. 在具有重复纹理和低纹理的海底图像中得到的成功说明了该方法的可行性和有效性.

6 结束语

根据海底图像拼接需要正确且数量多的特征对应点的要求, 本文提出了海底图像预处理方法, 介绍了相应的步骤及效果; 然后提出了一种针对机器人拍摄的海底序列图像的图像配准方法: 基于先验信息和图像信息的图像配准方法, 并于仅基于图像信息的海底图像配准进行配准点数目及正确率的比较, 在具有重复纹理和低纹理的海底图像上进行实验. 实验结果表明: 经过预处理之后, 海底图像光照不均匀, 对比度差的问题得到有效改善, 为后续图像配准做好准备. 相对于基于图像信息的序列海底图像配准, 本文方法有效的降低了匹配对应的误配率, 增加了对应点的数目, 满足了海底图像拼接的后续要求, 为水下视觉在海底探索中的应用提供了帮助.