2. 武汉大学 测绘遥感信息工程国家重点实验室, 武汉 430079
2. State Key Laboratory of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
东洞庭湖国家级自然保护区位于长江中游荆江江段南侧, 是典型的湿地生态系统, 也是我国首批进入“国际重要湿地公约”的湿地之一. 作为洞庭湖湖系中最大的湖泊, 东洞庭湖气候温和湿润, 孕育了鸟类、鱼类、植物等丰富的物种资源, 也是重要的渔业生产基地, 对长江流域的水位调控起重要作用. 近年来, 由于人类经济活动和长江中游地区洪旱灾害的影响, 东洞庭湖的水文和水质特征发生一定变化, 生物多样性受到威胁, 调洪蓄水功能下降. 水位-水体面积关系是描述湖区水情变化的指标之一, 对湖区生态环境的保护和政策制定有重要意义.
易波琳等[1]通过解译岳阳和常德的TM影像和计算机面积量算, 再应用最小二乘法原理, 求得洞庭湖内各湖面积与水位的回归方程. 彭定志等[2]利用NDVI对MODIS影像进行水体面积的计算, 得到洞庭湖水位-面积曲线. 杜涛等[3]利用2010年3种质量较好的MODIS影像数据, 分别运用NDVI和RVI进行水体提取, 拟合出面积-水位曲线. 黄一凡等[4]利用ENVI + IDL 4.7, 对332个时相的MOD13Q1影像数据进行批量分类处理, 得到东洞庭湖水体湿地面积统计数据, 从而建立岳阳水文站和水体面积的回归方程. 柯文莉等[5]利用MRT (MODIS Reprojection Tool) 软件, 对MODIS L1 B数据进行波段提取、几何纠正、投影转换, 用ENVI进行重采样、影像裁剪等, 得到研究区影像数据, 再利用NDWI提取水体. 众多学者不断改进东洞庭湖水位-面积关系的研究方法, 但是已有的研究在进行水体提取时下载与处理数据繁琐, 需要使用许多专业软件, 且数据存储量大, 人工干预较多, 耗时长, 处理效率低, 不适合长时间尺度的地理分析和应用[6]. 因此, 需要提高水体提取的工作效率.
Google Earth Engine (GEE)是由Google建立的处理遥感数据的云端计算平台, 提供大量地球观测数据, 具有极强的数据存储和处理能力[7]. 用户通过应用编程接口API可以进行算法编写、数据集生产和地理空间分析等. GEE可以有效解决数据获取困难、数据处理复杂耗时等问题, 提高用户的工作效率.
鉴于此, 本文基于Google Earth Engine, 选择2001年至2016年的Landsat遥感影像, 利用NDWI模型提取东洞庭湖水体面积, 根据城陵矶水文站实测水位信息, 建立东洞庭湖水位-水体面积的关系曲线.
1 研究区域与数据 1.1 研究区域简介东洞庭湖(29°00′ N至29°38′ N, 112°43′ E至113°14′ E)位于湖南省北部岳阳市, 地处长江中游荆江南侧, 属于亚热带湿润季风气候, 拥有充足的日照, 降水量年际变化大. 东洞庭湖是洞庭湖湖区中保存最为完好的季节性湖泊, 也是长江上重要的调蓄湖泊[2]. 湖区设有湖南东洞庭湖国家级自然保护区, 1992年加入《国际重要湿地公约》, 1994年升级为国家级自然保护区, 是我国典型的湿地生态环境. 城陵矶水文站是长江流域135个水文站之一, 位于洞庭湖与长江的交汇处, 对长江流域防汛测报起重要作用. 图1为东洞庭湖区域Landsat影像合成图.
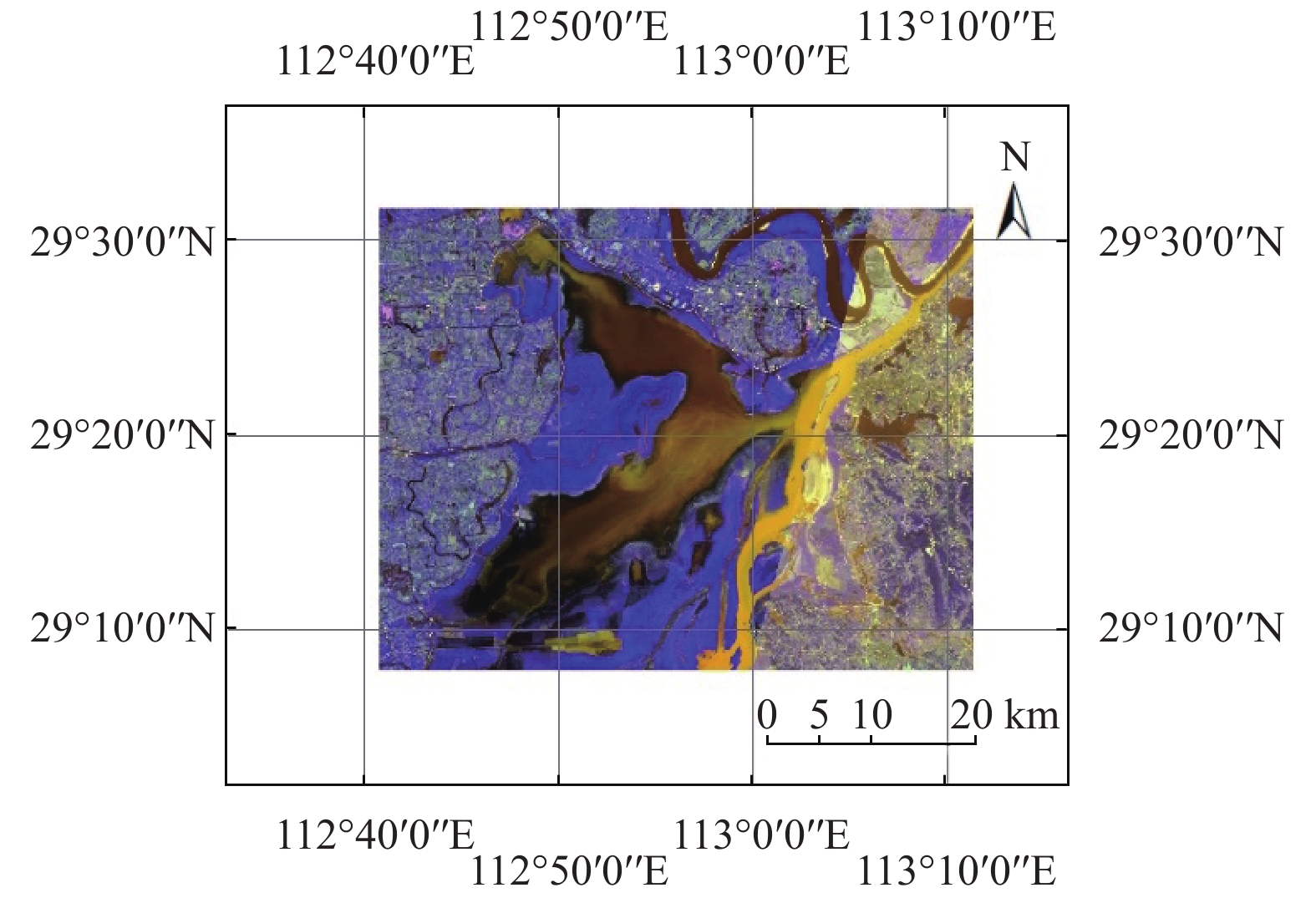
|
图 1 东洞庭湖区域 |
1.2 Google Earth Engine平台简介
Google Earth Engine (GEE)又称谷歌地球引擎, 是一个基于云操作的平台, 支持快速、交互式探索和分析空间数据. GEE包含大量公开的地理空间数据集, 除了Landsat、MODIS、Sentinel等遥感影像数据外, 还提供地形数据、土地覆盖数据、气象数据、地球物理数据和社会经济数据等. 用户通过应用程序编程接口(API)和基于Web的交互式开发环境(IDE)进行访问控制, 可使用Python和JavaScript语言编写和调用算法, 利用该平台的高性能计算资源处理大型空间数据集[7].
Google Earth Engine主要从以下方面提高用户工作效率: (1)数据易得: 用户不需要自行采集、存储和管理遥感数据, 可直接调用平台提供的地理数据集; (2)数据处理方便: 平台提供图像处理、机器学习和地理统计等操作, 用户通过函数式编程环境对地理信息进行分析; 平台提供大量CPU的编组和管理, 用户无需提供硬盘和服务器; 平台利用Java Just-In-Time (JIT)编译器优化逐像素操作链的执行; (3)结果共享: 平台可方便用户将研究结果传播给其他研究人员、政府工作者和普通公众等.
1.3 实验数据及处理本文数据有两类: (1)影像数据: 选用2002年至2016年东洞庭湖区域的Landsat遥感影像作为原始影像数据, 包括Landsat 5影像63景, Landsat 8影像34景, 一共97景影像. 利用Google Earth Engine平台进行数据下载, 编程完成辐射定标、几何校正、大气校正、去云处理、影像拼接、掩模去除建筑区等预处理. 由于东洞庭湖常年处于多云天气, 很难获得连续的无云影像, 因此需要将不同时期的少云影像进行拼接, 最后得到处理后的2002年至2016年东洞庭湖影像数据36景, 每一景为3个月的拼接合成影像. (2)水位数据: 城陵矶水文站水位数据来源于湖南省水利厅水文信息网, 包括水位采集时间、逐日水位(以米为单位).
2 研究方法 2.1 基于NDWI的水体提取常用的水体提取方法有单波段阈值法、谱间关系法和指数法等. 单波段阈值法在TM5波段影像上选择一个阈值进行水体提取, 原理简单, 但水体与非水体的交界区域提取效果差[8]. 谱间关系法利用多个波段影像信息, 能有效区分水体和阴影, 适合地势起伏较大的地区, 而在平原地区优势不明显[9]. 指数法根据研究地类在各波段反射率的强弱, 通过比值运算突出感兴趣地物.
NDWI(Normalized Difference Water Index)指数对湖泊等大块水体的提取效果好, 可以突出水体特征, 抑制非水体特征[10]. EI-Asmar 等[11]利用NDWI研究尼罗河三角洲水体面积. 李文波等[12]利用NDWI从ETM+遥感数据中提取水体. 根据徐蓉等[13]采用3种方法对我国不同地区的10个湖泊进行水体提取的结果,NDWI比波段插值模型适合东部地区湖泊提取. 根据张飞等[14]对新疆艾比湖水体提取的结果, NDWI比MNDWI精度更高. 对于内陆湖泊, 利用NDWI指数水体提取效果好, 因此选用NDWI进行水体提取.
NDWI 利用水体在绿光反射率最大、水体在近红外波段反射率小、植被土壤在近红外波段反射率大的特征, 根据式(1)在包含绿波段和近红外波段的影像中提取水体[15]. 一般而言, 当NDWI指数为正值时, 判断地物为水体; 当NDWI指数为零值或负值时, 判断为植被或土壤. 实际情况中水体含有叶绿素、悬浮物等物质, 因此要根据研究区域的具体情况设定合适的阈值.
| $ NDWI = \frac{{GREEN - NIR}}{{GREEN + NIR}} $ | (1) |
式中,GREEN为Landsat数据在绿波段的反射率,NIR为Landsat数据在近红外波段的地表反射率.
确定阈值是利用NDWI区分水体和非水体的重要步骤, 但是水体和其他物体之间的阈值不稳定, 且随着场景和位置的变化而变化, 因此为每个图像手动寻找阈值是不切实际的. Otsu阈值被广泛用于确定NDWI在水体检测的阈值[16]. Otsu方法从图像直方图中确定理想阈值, 使类间方差最大, 类内方差最小. 选择Otsu方法自动确定每个月的阈值, 共得到12个阈值(见表1), 根据阈值判断地面像元是否为水体, 减少因不同时期水文特征不同造成水体信息提取遗漏现象. 当像元NDWI大于阈值时, 判断该像元为水体, 当像元NDWI小于阈值时, 判断该像元为非水体. 由于预处理后的Landsat影像为拼接影像, 包含两个或两个以上日期的水位信息, 因此一幅影像上使用的NDWI阈值同样多于一个. 利用Google Earth Engine平台, 完成不同阈值的水体提取, 得到东洞庭湖地区水体提取结果的二值化图像36幅.
| 表 1 NDWI阈值 |
2.2 水位与水体面积关系建立方法
本文使用Landsat数据作为影像数据, 由于Landsat影像空间分辨率为30 m, 因此利用单个像元的面积(30 m×30 m = 900 m2= 0.0009 km2)乘水体像元个数可计算出东洞庭湖水体的总面积. 根据预处理后得到的Landsat影像日期信息, 可以找到每幅影像对应的城陵矶水文站水位信息.
根据原始Landsat影像的日期, 将东洞庭湖水体面积序列与对应的水位值序列进行配对, 得到水位-水体面积组. 由于一幅影像对应多个水位值(1~n), 因此在进行水位-水体面积函数关系的确定时, 设计3种方法得到水体提取结果对应的最佳水位值, 再通过线性函数、指数函数、对数函数、多项式函数等方式建立最优水位-水体面积关系曲线.
第1种方法为水位加权平均法. 水体提取的结果取决于该区域不同时期的拼接影像, 拼接区域的大小直接影响提取结果, 因此不同时期的水位对该影像水位信息的贡献有差异. 基于对各日期水位值贡献率的综合考虑, 将水体影像中各个水位值(即各个日期的影像区域)所占面积的比重作为权重, 得到加权平均的水位值(如式(2))作为最佳水位.
| $ {{L = }}\sum\limits_{j = 1}^m {\frac{{{a_j}}}{a} \times {l_j}} $ | (2) |
式中,
第2种方法为单点水位法. 由于城陵矶水文站位于东洞庭湖与长江的交界处, 同时也处于水体提取的边界区域, 相对于东洞庭湖其他区域, 该水文站所在像元的水位值对水体提取的结果贡献更大. 因此, 选用该像元水位代表东洞庭湖区域的水位值. 首先确定影像中城陵矶水文站所在位置的影像日期, 再选取该日期的水位值为最优水位.
第3种方法为阈值法. 东洞庭湖水情特征比较复杂, 按照水情的变化可以分为涨水期、退水期、丰水期和枯水期, 每个时期的平均水位值差距较大[4]. 对于不同水文时期的东洞庭湖区域, 采用不同的标准来确定最优水位. 为便于分析, 将东洞庭湖水文时期分为两类: 丰水期和枯水期. 丰水期水位值相对更大, 枯水期水位值相对更小. 根据水位-水体面积的统计信息, 确定一个面积阈值将水位-水体面积序列分为两类. 如果水体面积大于该阈值, 视为丰水期, 选取影像最大水位值作为最优水位; 如果面积小于该阈值则视为枯水期, 则取影像最小水位值作为最优水位.
2.3 精度评价对于水位-水体面积函数关系, 使用确定性系数R2(见式(3))进行拟合方程的精度评定.
| $ {{{R}}^2}{\rm{ = }}\left( {1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({{\hat a}_i} - {a_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({{\bar a}_i} - {a_i})}^2}} }}} \right) \times 100{\text{%}} $ | (3) |
式中,
Landsat影像预处理后得到36景东洞庭湖影像数据, 根据选取的NDWI阈值, 利用Google Earth Engine提取水体.
利用定量统计分析方法, 随机选取其中4景影像的水体提取结果作为样本进行精度评价. 首先, 基于Google Earth Engine在影像上选取300个随机点, 其次, 将原始影像与NDWI提取结果进行叠加分析, 通过混淆矩阵法计算水体提取精度(如表2).
| 表 2 水体提取结果与精度评价 |
从表2可看出, 水体提取结果的总体精度都超过95%, Kappa系数大于0.9, 说明NDWI进行水体提取的结果理想, 利用Ostu方法得到的NDWI阈值可以准确提取东洞庭湖水体面积.
从图2提取结果可知, 随着季节的变化, 东洞庭湖水体面积变化较大, 最小面积常出现在春季(1~3月), 夏季(4~6月)开始上升, 到秋季(7~9月)时湖面面积达到一年的最大值, 在冬季(10~12月)水面积逐渐减小. 研究时间内的最大面积为 1204.7517 km2 (2002年7~9月), 最小面积为240.7221 km2 (2008年1~3月). 春季平均面积为332.6463 km2, 夏季平均面积为715.1662 km2, 秋季平均面积为1078.1585 km2, 冬季平均面积为696.5282 km2. 由提取影像面积变化可以看出, 东洞庭湖是一个季节性的湖泊.
3.2 东洞庭湖水位与水体面积关系使用水位加权平均法、单点水位法和阈值法(根据统计值确定阈值为750 km2)这3种方法对每幅水体提取影像进行计算, 得到最佳水位-水体面积序列, 如表3所示. 由计算可知, 加权平均水位法与阈值法的相关系数为88.67%, 单点水位法与阈值法相关系数为90.80%, 加权平均水位法与单点水位法的相关系数为86.11%. 3种水位序列相关性不大于95.00%, 具有一定差异性.

|
图 2 东洞庭湖水域水体提取结果 |
利用线性函数、指数函数、对数函数、三次多项式、五次多项式这5种函数模型, 以最优水位值为横坐标, 东洞庭湖水体面积为纵坐标, 建立最优水位-水体面积关系曲线. 由关系曲线(如图3)可知, 水体面积随水位增长整体呈上升趋势.
使用3种方法求解得到5种模型的确定性系数R2如表4所示. 由表4可看出, 阈值法拟合的水位-水体面积函数模型精度最好, 大部分模型优于其他方法的模型, 且5种模型的确定性系数均大于90%. 分析原因, 由于水体影像由同一季节若干幅不同日期的影像拼接而成, 在3个月内水位变化可能较大(如2016年9月25日与2016年7月23日水位差为10.07 m), 如使用加权平均水位值或单点水位法则不能准确表达该季节水位情况. 使用阈值法选择最优水位可在一定程度上避免此类情况.
对比阈值法的5种模型, 可知五次多项式模型(如式(4))确定性系数最高, 其次是三次多项式模型、线性函数模型、对数函数模型, 指数函数模型确定性系数最低.
| $ \begin{split} a =& 0.0577{l^5} - 7.5095{l^4}+ 386.76{l^3} \\ & - 9854.6{l^2} + 124\;268l - 620\;522 \\ \end{split} $ | (4) |
其中, l为东洞庭湖水位值, a为东洞庭湖水域面积.
由五次多项式模型拟合的水位-水体面积函数关系曲线(如图4)可知, 88.89%的水体面积拟合误差小于50 km2, 94.44%的水体面积拟合误差小于100 km2, 五次多项式模型拟合结果较好. 水位值在23 m至29 m之间时拟合效果最好, 拟合误差较大的时期集中在秋季(7~9月)和春季(1~3月). 该模型对水体面积在250 km2至1200 km2范围外的水位-面积序列拟合误差较大, 不适用于水体面积过大或过小的湖区情况.
| 表 3 最佳水位-水体面积序列 |
与前人的研究对比, 本文水位-水体面积关系建立方法主要有3点优势:
(1)探索合成影像上多个水位值与水体面积的关系. 由于拼接影像由多个不同时间采集的影像合成, 对应多个水位值, 现研究主要选取无云影像或质量较好的影像, 很少对拼接影像进行研究, 因此实际可用的影像数量较少, 直接影响水位-水体面积模型精度. 如何将拼接影像的多个水位值与获取的水域面积建立关系, 本文进行了探索, 设计并讨论3种水位选取方法, 提高了研究时间范围内遥感影像的利用率, 同时在一定程度上避免了拼接影像水位选取的误差.
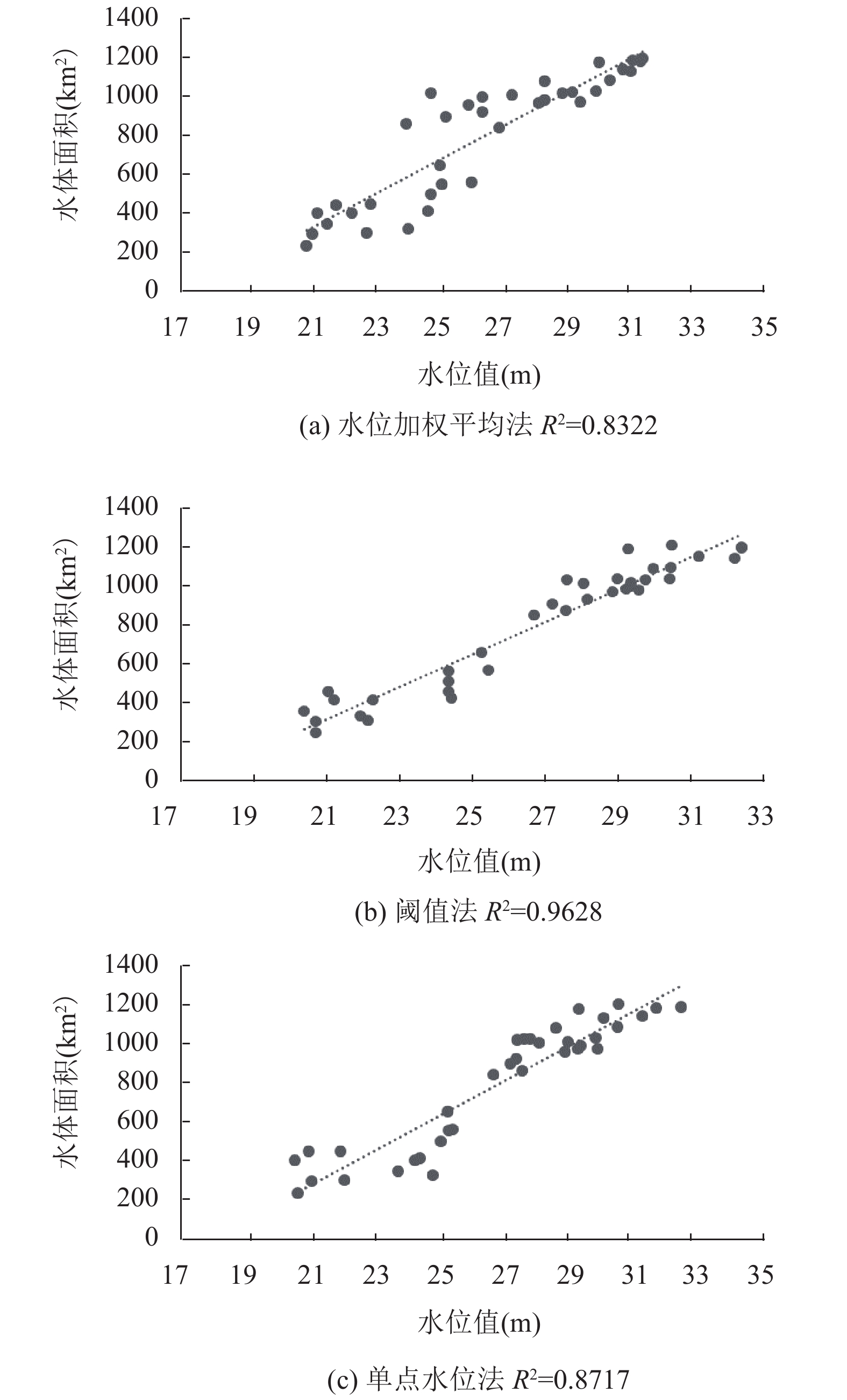
|
图 3 东洞庭湖水位-水体面积线性模型对比图 |
| 表 4 3种方法的确定性系数(R2) |
(2)影像数据量大, 时间尺度大. 受到影像质量和处理效率的限制, 现研究多采用小尺度时间序列(某年或数年内)的若干幅遥感影像进行分析, 水位-水体关系模型样本少, 且存在时间上的局限性, 无法满足对长时间序列关系研究的要求. 本文基于Google Earth Engine高效处理并得到较大数据量的影像数据, 所建立的水位-水体关系模型时间尺度大, 为东洞庭湖区域长期水资源变化研究和管理提供依据.
(3)模型精度高. 柯文莉等[4]对2000至2012 年东洞庭湖水面面积与城陵矶水位月平均绳套曲线进行研究, 得到R2为93.7%. 宋求明等[17]利用二次多项式对2003至2006年洞庭湖水位-面积关系进行研究, 得到R2为91.32%. 本文利用阈值法选取影像最优水位值, 利用五次多项式模型得到R2为96.28%, 说明该方法更加准确地反映实际水位与湖泊水体面积关系.
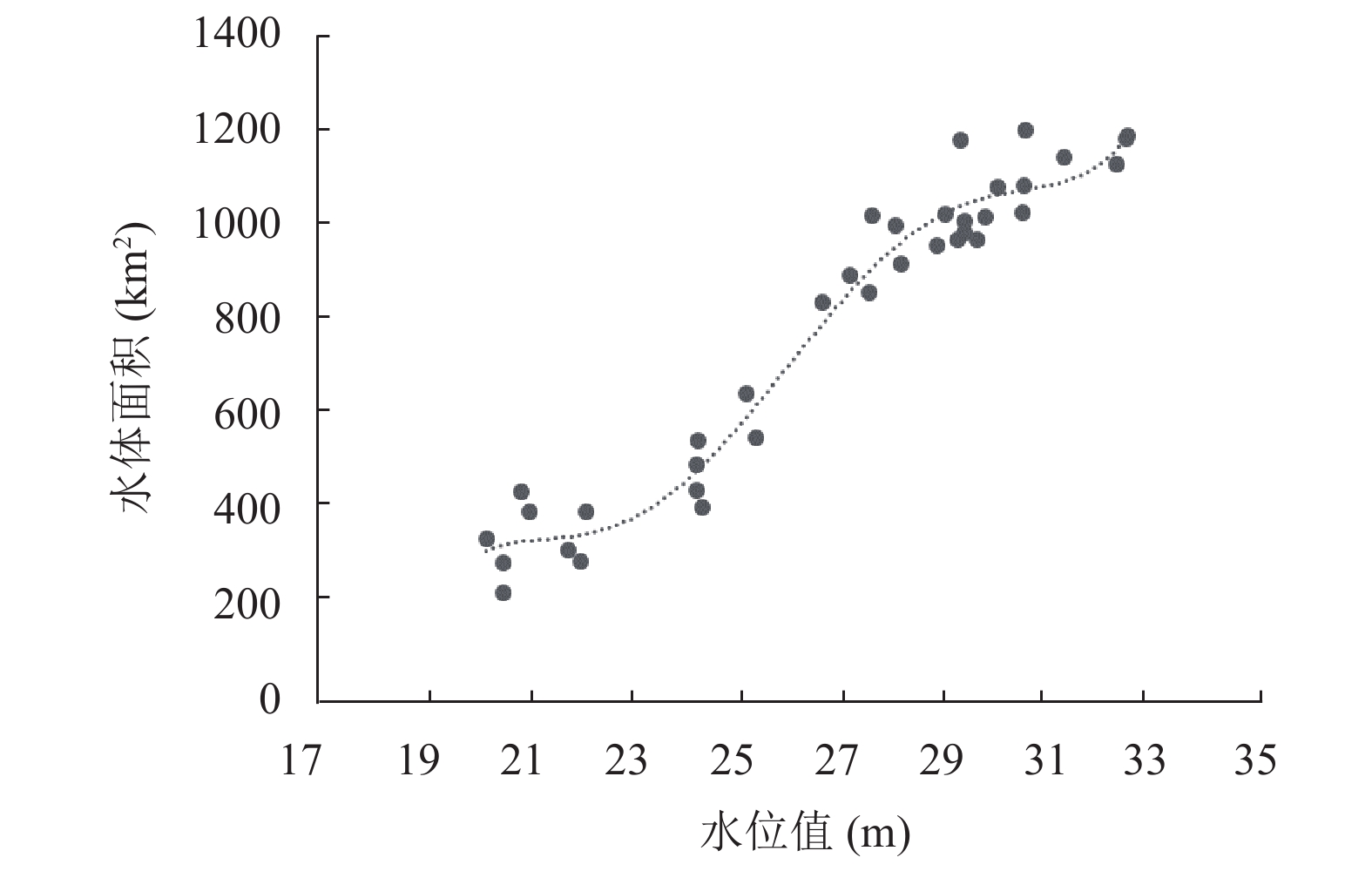
|
图 4 阈值法五次多项式模型拟合方程(R2=0.9628) |
4 结语
本文基于Google Earth Engine平台, 利用长时间序列的东洞庭湖区域Landsat历史影像, 使用NDWI阈值法提取水体得到东洞庭湖水体面积, 探索影像所对应的最优水位值, 确定水位-水体面积关系曲线模型, 得到以下结论:
(1) Google Earth Engine平台可以高效下载并处理大量的遥感数据, 具有很强的计算能力.
(2)根据东洞庭湖的水文特征, 利用Otsu方法确定利用12个月阈值分别为0.08、0.06、0.03、0.01、0.00、0.00、0.00、0.00、0.01、0.02、0.05、0.08的NDWI值进行水体提取和面积计算. 东洞庭湖水域面积随季节变化大, 冬夏差异明显, 7~9月水域面积最大(平均面积为1078.1585 km2), 1~3月水域面积最小(平均面积为332.6463 km2). 研究时期内最大面积为1204.752 km2, 最小面积为240.722 km2.
(3)设计3种方法确定影像水位, 经实验得到利用阈值法计算影像最优水位值的效果最好(最大R2为0.9628), 优于加权平均水位法(最大R2为0.8322)和单点水位法(最大R2为0.9457). 对于阈值法计算的最优水位值, 通过五次多项式模型建立的水位-水体面积函数关系精度最高(R2=0.9628), 优于线性函数(R2=0.9317)、指数函数(R2=0.908)、对数函数(R2=0.9287)和三次多项式(R2=0.9566).
| [1] |
易波琳, 李晓斌, 梅金华. 洞庭湖面积容积与水位关系及调蓄能力评估. 湖南地质, 2000, 19(4): 267-270. |
| [2] |
彭定志, 徐高洪, 胡彩虹, 等. 基于MODIS的洞庭湖面积变化对洪水位的影响. 人民长江, 2004, 35(4): 14-16. DOI:10.3969/j.issn.1001-4179.2004.04.006 |
| [3] |
杜涛, 熊立华, 易放辉, 等. 基于MODIS数据的洞庭湖水体面积与多站点水位相关关系研究. 长江流域资源与环境, 2012, 21(6): 756-765. |
| [4] |
黄一凡, 王金生, 杨眉. 基于水位-面积-湖容关系的东洞庭湖动态纳污能力分析. 长江科学院院报, 2018, 35(9): 12-16. DOI:10.11988/ckyyb.20180533 |
| [5] |
柯文莉, 陈成忠, 吉红霞, 等. 洞庭湖水面面积与城陵矶水位之间的绳套关系. 湖泊科学, 2017, 29(3): 753-764. DOI:10.18307/2017.0325 |
| [6] |
张滔, 唐宏. 基于Google Earth Engine的京津冀2001~2015年植被覆盖变化与城镇扩张研究. 遥感技术与应用, 2018, 33(4): 593-599. |
| [7] |
Gorelick N, Hancher M, Dixon M, et al. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sensing of Environment, 2017, 202: 18-27. DOI:10.1016/j.rse.2017.06.031 |
| [8] |
黎慧, 赵阳. 基于TM影像水体提取方法比较研究. 科学大众(科学教育), 2018(9): 195-196. |
| [9] |
毕海芸, 王思远, 曾江源, 等. 基于TM影像的几种常用水体提取方法的比较和分析. 遥感信息, 2012, 27(5): 77-82. DOI:10.3969/j.issn.1000-3177.2012.05.014 |
| [10] |
王志辉, 易善桢. 不同指数模型法在水体遥感提取中的比较研究. 科学技术与工程, 2007, 7(4): 534-537. DOI:10.3969/j.issn.1671-1815.2007.04.028 |
| [11] |
El-Asmar HM, Hereher ME, El Kafrawy SB. Surface area change detection of the Burullus Lagoon, North of the Nile Delta, Egypt, using water indices: A remote sensing approach. The Egyptian Journal of Remote Sensing and Space Science, 2013, 16(1): 119-123. DOI:10.1016/j.ejrs.2013.04.004 |
| [12] |
李文波, 于春颖, 张秋文, 等. 基于归一化水体指数的水域面积估算研究. 人民长江, 2008, 39(2): 11-12, 36. DOI:10.3969/j.issn.1001-4179.2008.02.004 |
| [13] |
徐蓉, 张增祥, 赵春哲. 湖泊水体遥感提取方法比较研究. 遥感信息, 2015, 30(1): 111-118. DOI:10.3969/j.issn.1000-3177.2015.01.019 |
| [14] |
张飞, 王娟, 塔西甫拉提·特依拜, 等. 1998-2013年新疆艾比湖湖面时空动态变化及其驱动机制. 生态学报, 2015, 35(9): 2848-2859. |
| [15] |
McFeeters SK. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. International Journal of Remote Sensing, 1996, 17(7): 1425-1432. DOI:10.1080/01431169608948714 |
| [16] |
袁欣智, 江洪, 陈芸芝, 等. 一种应用大津法的自适应阈值水体提取方法. 遥感信息, 2016, 31(5): 36-42. DOI:10.3969/j.issn.1000-3177.2016.05.006 |
| [17] |
宋求明, 熊立华, 肖义, 等. 基于MODIS遥感影像的洞庭湖面积与水位关系研究. 节水灌溉, 2011(6): 20-23, 26. |
 2021, Vol. 30
2021, Vol. 30



