人脸作为重要的生物学特征, 在人际交流中传达着丰富的信息. 从面部表情的角度来看, 人脸表情包含着丰富的情感以及心理信息, 是一种重要的非语言交流方式. 另外, 还可以从人的面部识别出人的性别, 年龄, 种族和其他特征. 目前, 关于面部表情分类的研究已受到国内外许多著名大学, 研究机构和公司的重视, 这主要是由于其重要的理论研究意义和广泛的应用场景. 20世纪60年代, 国外学者提出了基于人脸的几何特征识别方法用于图像分类. 在90年代由Belhumeur提出的线性判别分析(LDA)[1]成为了当时颇具代表性的人脸识别算法. 研究者们在此算法基础上研究产生了许多改进算法, 比如并行LDA算法、基于概率延伸公式的LDA算法、直接的LDA判别方法以及近期的一些基于核学习的改进攻略[2]. 后来Yang等[3]提出基于稀疏表示(SRC)理论的分类方法开始应用到了面部识别中.
在人脸表情分类的过程中, 面部表情特征的提取将会很大程度地影响到最终的分类效果. 常用的特征提取方法有基于几何特征的方法、模板匹配法(ASM)[4]、弹性图匹配(DLA)[5]、局部二值模式(LBP)[6]以及Gabor小波变换[7]等方法. 由于局部二值模式计算复杂度低以及能更好的体现图像纹理特征等优点, 被广泛地应用于图像分类等领域中. 在分类识别方面, 常用的有K最近邻(KNN)[8]、支持向量机(SVM)[9]、卷积神经网络[10]等分类器. 2011年由国内学者Zhang等[11]提出了协作表示分类算法, 极大地提高了算法的识别速度使得基于表示的分类方法成为研究焦点. 但是文献[8,9]均未对图像数据进行预处理而是直接采用相关算法进行分类, 未能解决在图片分类时效率低下及准确率较低的问题. 目前人脸表情分类存在着多种挑战, 往往都是由于人脸表情的复杂度、多样性、多变性等造成人脸特征的显著改变. 随着年龄的增加, 人脸皱纹的出现和面部肌肉的松弛使得人脸的结构和纹理都将发生改变, 另外人脸的部分遮掩也将会造成错误分类. 同时由于光照、视角、摄取角度的不同, 可能会造成图像的灰度畸变、角度旋转等, 这些都极大地增大了分类的难度.
针对上述的缺点, 本文提出了一种基于改进的协作表示人脸表情分类算法. 其算法的主要步骤为: 首先采用分块加权局部二值模式对图像进行分块预处理, 得到每个子块的特征向量. 为了避免维度灾难, 接着使用主成分分析法对特征向量进行降维处理, 最后使用竞争协作表示分类算法对图像进行分类.
竞争协作表示是在经典的协作表示算法中引入样本竞争的思想, 增强训练样本与测试样本之间的关联, 从而提高算法的学习能力, 进而得到更高的分类精度.
2 局部二值模式(LBP)LBP算法的核心思想是, 针对图像中的每一个像素点, 以图像中心像素点的灰度值作为阈值进行编码, 并用相邻像素点灰度值与其进行比较, 将灰度值小于阈值的编码为0, 大于阈值的则编码为1[12]. 然后按顺时针方向将编码后的二进制码组合排列, 之后将二进制码转化为对应的十进制值, 以该十进制值作为区域中心像素灰度值的编码. 以3×3区域为例由此可以计算得到LBP编码如图1所示.
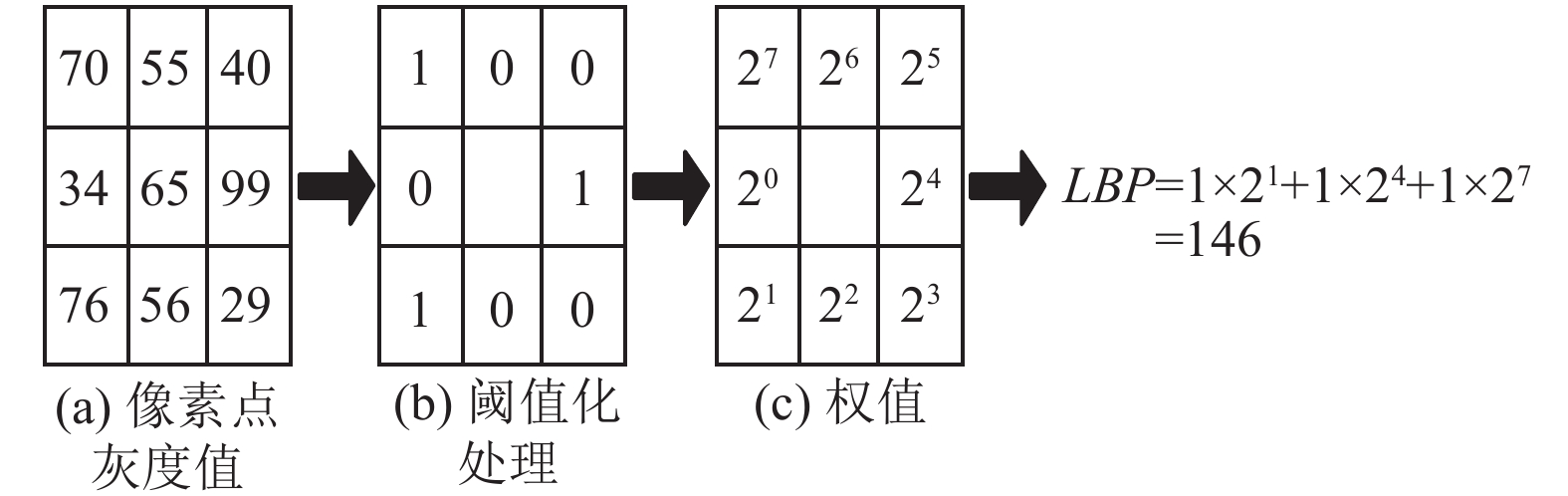
|
图 1 LBP编码计算 |
LBP算法的优势在于对人脸的纹理特征有着较好的提取能力, 特别是局部的一些暗点、亮点、边缘特征等有良好的表述性能[13]. 缺点是随着邻域内采样点的数量增加, 经过编码后的模式种类会以指数形式增长, 大大增加了存储空间, 同时也会使计算效率大幅下降.
3 分块加权LBP绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变. 因此“均匀模式”定义为: 当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时, 该LBP所对应的二进制就称为一个均匀模式类[14]. 通过这样的改进, 模式数量直接降为
在同一张人脸图片中, 不同的区域所包含的纹理信息差异是非常大的. 为了能进一步的区分不同区域的纹理信息从而体现更好的局部特征, 对图像采取分块处理并对每个分块进行了加权, 通过计算和比较块与块之间的纹理熵, 将不同子块纹理熵的值作为加权因子以区分不同子块所代表的信息[15]. 最终将加权后各个子块的特征向量组合起来构成一个联合特征向量作为该图像的特征向量.
假设将图像分为n个子块, 第i个子块的纹理熵可以表示为:
| $Hi = - \sum\limits_{k = 1}^{256} {p_i^k\log 2p_i^k} $ | (1) |
其中, k表示像素的灰度级,
| ${\omega _i} = \frac{{Hi}}{{\displaystyle\sum\limits_{i = 1}^n {Hi} }}$ | (2) |
设
| $H = [{\omega _1}{h_1},{\omega _2}{h_2},\cdots,{\omega _n}{h_n}]$ | (3) |
假设一共有n个训练样本可以被分成c类, 属于第i类
在基于协作表示的分类算法中, 可以将
| $\mathop {\min }\limits_\alpha \{ {\rm{||}}\alpha {\rm{|}}{{\rm{|}}_2}\}\;\; {\rm{s.t.}}\;\; ||y - X\alpha |{|_2} \le \varepsilon $ | (4) |
| $ \mathop {\min }\limits_\alpha \left\{ { ||y - X\alpha ||_2^2 + \lambda ||\alpha ||_2^2} \right\} $ | (5) |
第1项
将式(5)展开, 得到:
| $\mathop {\min }\limits_\alpha \left\{ { {y^{\rm{T}}}y - 2{y^{\rm{T}}}X\alpha + {\alpha ^{\rm{T}}}{X^{\rm{T}}}X\alpha + \lambda \left( {{\alpha ^{\rm{T}}}\alpha } \right)} \right\} $ | (6) |
对式(6)中的系数
| ${\rm{ - }}2{X^{\rm{T}}}y + 2{X^{\rm{T}}}X\alpha + 2\lambda \alpha = 0$ | (7) |
约去式(7)中的公因子:
| ${\rm{ - }}{X^{\rm{T}}}y + {X^{\rm{T}}}X\alpha + \lambda \alpha = 0$ | (8) |
对式(8)进行化简可得:
| ${X^{\rm{T}}}X\alpha {\rm{ + }}\lambda \alpha {\rm{ = }}{X^{\rm{T}}}y$ | (9) |
求解式(9)得到重构系数的最优解:
| $ \alpha \left( {X^{\rm{T}}}X + \lambda I \right)^{ - 1}{X^{\rm{T}}}y $ | (10) |
其中,I是一个单位矩阵, 令
| ${r_i}(y) = \frac{{||y - {X_i}{\alpha _i}|{|_2}}}{{||{\alpha _i}|{|_2}}}$ | (11) |
通过式(11)来衡量类别为i的训练样本与测试样本的相似度, 当重构误差越小, 则表明训练样本与测试样本之间的相似度越高, 结果对应的就是测试样本属于第i类的可能性就越高, 最终的测试样本的分类可以表示为:
| $identity(y) = \mathop {\arg \min \{ {r_i}(y)\} }\limits_i $ | (12) |
竞争协作表示(CCRC)首先是由Yuan等[17]提出. 该算法针对在协作表示(CRC)中, 由于是使用所有的训练样本来表示测试样本以及使用每一类中的训练样本表示测试样本是相互独立的过程从而忽略了它们之间的联系, 即式(4)和式(11)是相互独立的, 因此将其结合起来作为一个整体, 在原有模型的基础上加入新的正则项, 模型表示如下:
| $\mathop {\min }\limits_\alpha \left\{ { ||y - X\alpha ||_2^2 + \lambda ||\alpha ||_2^2 + {\lambda _1}\sum\limits_{i = 1}^c {||y - {X_i}{\alpha _i}||_2^2} } \right\}$ | (13) |
式(13)中, 第1项是用所有的训练样本来表示测试样本(称为协作性), 第3项是用每个类中的训练样本来重构测试样本(称为竞争性),
| $\alpha {\rm{ = }}Py$ | (14) |
| $P = (1 + {\lambda _1}){\left( {{X^{\rm{T}}}X + \lambda I + {\lambda _1}M} \right)^{ - 1}}{X^{\rm{T}}}$ | (15) |
| $ M = \left[ {\begin{array}{*{20}{c}} {{X_1}^{\rm{T}}{X_1}}& \cdots &0 \\ \vdots & \ddots & \vdots \\ 0& \cdots &{{X_c}^{\rm{T}}{X_c}} \end{array}} \right] $ | (16) |
将重构误差定义为:
| ${r_i}(y) = ||y - {X_i}{\alpha _i}|{|_2}$ | (17) |
运用式(10)计算测试样本和每一类别训练样本之间的重构误差, 将重构误差
针对协作表示分类精度有待提高, 本文提出一种改进的协作表示分类算法, 算法首先采用均匀模式下的分块加权局部二值模式提取图像特征, 接着使用主成分分析法对训练样本和测试样本的特征向量进行降维, 最后运用竞争协作表示分类算法对图片进行分类. 具体步骤如下:
步骤1. 对所有图片样本进行归一化处理为130×130像素大小.
步骤2. 将预处理过后的图片样本划分成为互不重叠的3×3, 4×4以及5×5三种分块方式, 采用分块加权LBP算法来提取特征向量.
步骤3. 运用主成分分析法对特征向量进行降维构成最终的训练样本和测试样本矩阵.
步骤4. 使用竞争协作表示分类器对图片进行分类.
步骤5. 为了使实验的结果更具可靠性, 使用10次交叉验证的方法重复实验10次得到最终分类的平均准确率.
7 实验结果与分析 7.1 实验环境实验计算机配置: CPU Core(TM)3.40 GHz, 内存16 GB, 显存8 GB; 操作系统: Windows7; 软件环境: Matlab 2017.
7.2 实验数据获取本次实验分为实验1和实验2.
实验1选取的数据为日本女性面部表情数据库. 该数据集中有7种表情, 每种表情大约有3–5幅图片, 总共有10个个体样本总数为213张图片. 选取10个个体每种表情各1幅图片总共70张图片作为测试样本, 其余的143张图片作为训练样本. 部分图像样例如图2所示.
实验2的数据来源为瑞典斯德哥尔摩心理学科卡罗琳斯卡情绪导向人脸表情数据库. 选取了其中的一个子集共计350张图片构成了样本数据集. 该数据集中有10个个体, 每个个体含有7种表情, 每种表情有5幅图片. 选取10个个体每种表情各1幅图片总共70张图片作为测试样本, 其余的280张图片作为训练样本. 部分图像样例如图3所示.

|
图 2 实验1数据库部分图像样例 |

|
图 3 实验2数据库部分图像样例 |
7.3 实验结果与分析
分别采用LBP+SRC, LBP+CRC, LBP+CCRC算法测试在不同分块模式以及不同特征维数情况下对图像的分类性能. 其中实验1的测试结果如图4至图6所示, 实验2的测试结果如图7至图9所示. 对测试结果展开分析.

|
图 4 实验1中3×3分块模式下的算法对比 |
(1)由图4至图9横向对比可知LBP+CCRC的分类效果在两个数据集中均优于LBP+SRC和LBP+CRC两种算法, 这是因为CCRC考虑到样本之间的竞争性从而能更好的表示相似样本之间的线性关系.

|
图 5 实验1中4×4分块模式下的算法对比 |

|
图 6 实验1中5×3分块模式下的算法对比 |

|
图 7 实验2中3×3分块模式下的算法对比 |
(2)同时从上述实验结果观察可以发现, 在5×3分块模式下各类算法的分类效果均优于3×3和4×4分块模式下的分类效果, 这是因为在5×3分块模式下对于纹理特征贡献度更大的子模块赋予了更多的权重从而提升了对图像的分类性能.
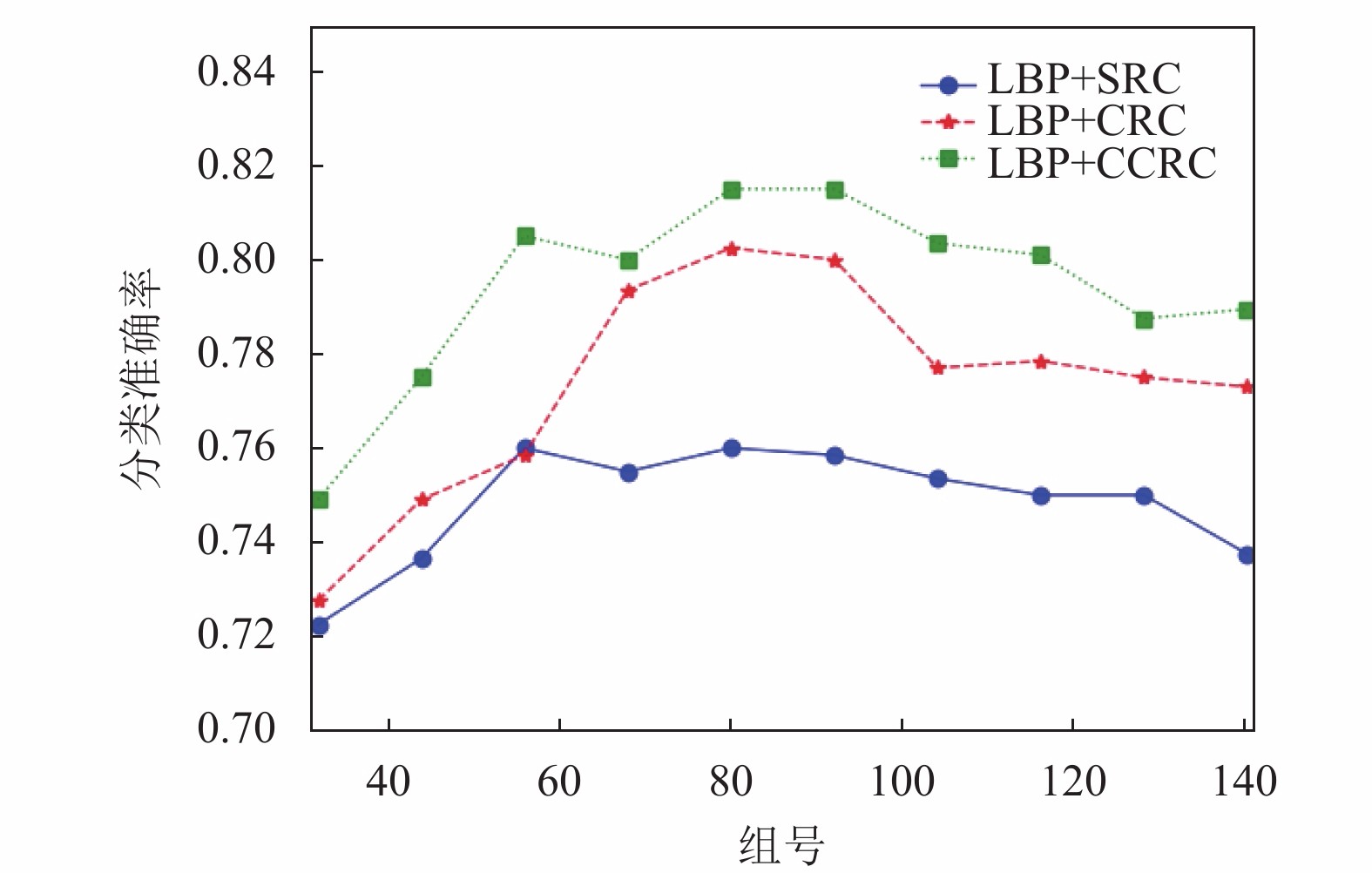
|
图 8 实验2中4×4分块模式下的算法对比 |
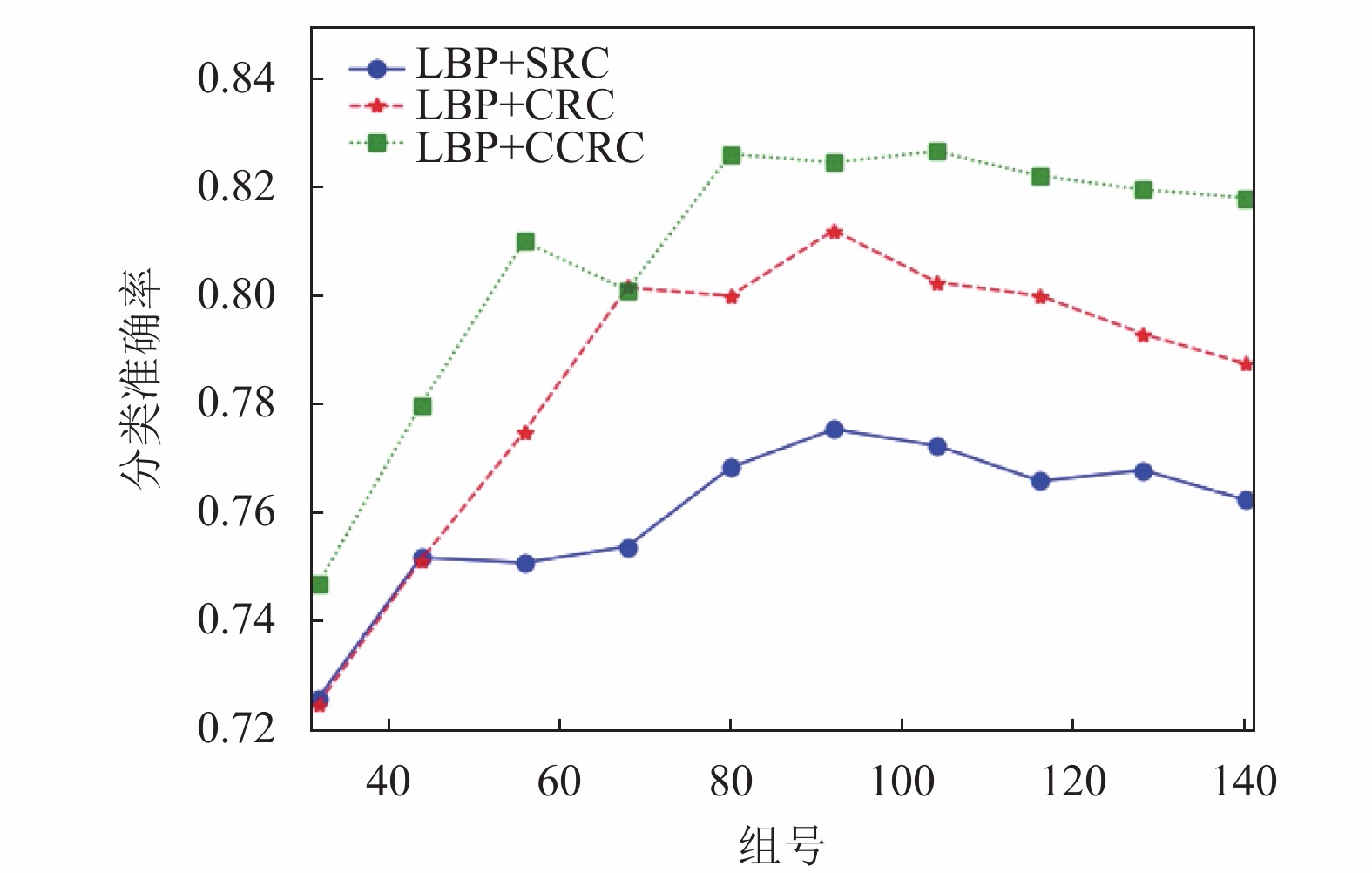
|
图 9 实验2中5×3分块模式下的算法对比 |
将不同算法的分类结果进行统计, 结果如表1.
为了说明分块加权LBP与基于协作表示算法的结合有着良好的分类效率, 将不同算法的运行时间进行统计, 结果如表2所示.
| 表 1 各数据集算法分类准确率对比(%) |
| 表 2 各数据集算法分类运行时间对比(单位: ms) |
从表2的实验结果可以看出, LBP与CRC相结合的算法跟LBP与CCRC相结合的算法在运行时间上较为接近, 相较于LBP与SRC相结合的算法缩短了将近50倍, 同时在不同分块模式下运行时间误差更小, 稳定性更强.
8 结论本文基于传统的CRC分类模型, 使用LBP+CCRC算法实现对原有算法的优化, 进而使得分类更加精准. LBP+CCRC算法在原有CRC算法上提出了两点改进: (1)采用分块加权的LBP算法对数据集中的训练样本和测试样本进行特征提取, 从而更好地描述人脸表情的局部细节纹理. (2)由于同一类别中的不同样本具有一定的相似性, 因此引入竞争的思想, 使用每一个类中的训练样本来重构测试样本以提高分类的准确率. 本文使用LBP+CCRC算法对日本女性面部表情和瑞典心理学科情绪导向表情两个数据库中的图片进行分类, 通过实验从表1可知LBP+CCRC算法相较于其他算法分类效果更为精准.
虽然引入了竞争的思想提高了分类的准确率, 但是在迭代的过程中也损耗了一定的时间, 因此在时间的损耗上还有待改进. 此外实验只考虑了3种分块模式下的分类情况, 未考虑其他的分块模式. 下一步的工作需要考虑更多的分块模式对实验的影响, 同时要将样本容量扩大, 另外也要在数据集中加入噪声在更多的情形下进行试验.
| [1] |
Yu H, Yang J. A direct LDA algorithm for high-dimensional data—with application to face recognition. Pattern Recognition, 2001, 34(10): 2067-2070. DOI:10.1016/S0031-3203(00)00162-X |
| [2] |
贺悦悦. 基于协同表示分类的人脸识别算法研究[硕士学位论文]. 秦皇岛: 燕山大学, 2017.
|
| [3] |
Yang JC, Wright J, Huang TS, et al. Image super-resolution via sparse representation. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873. DOI:10.1109/TIP.2010.2050625 |
| [4] |
陈皓, 马彩文, 陈岳承, 等. 基于灰度统计的快速模板匹配算法. 光子学报, 2009, 38(6): 1586-1590. |
| [5] |
刘晓东. 基于弹性图匹配法的人脸识别算法研究[硕士学位论文]. 上海: 上海交通大学, 2009.
|
| [6] |
Ahonen T, Hadid A, Pietikäinen M. Face recognition with local binary patterns. Proceedings of the 8th European Conference on Computer Vision. Prague, Czech Republic. 2004. 469–481.
|
| [7] |
Jain A K, Farrokhnia F. Unsupervised texture segmentation using Gabor filters. Proceedings of 1990 IEEE International Conference on Systems, Man, and Cybernetics Conference Proceedings. Los Angeles, CA, USA. 1990. 14–19.
|
| [8] |
Weinberger K Q, Blitzer J, Saul L K. Distance metric learning for large margin nearest neighbor classification. In: Weiss Y, Schölkopf B, Platt J, eds. Advances in Neural Information Processing Systems 18. Cambridge, Mass: MIT Press, 2006. 1473–1480.
|
| [9] |
Cauwenberghs G, Poggio T. Incremental and decremental support vector machine learning. Advances in Neural Information Processing Systems. Cambridge, UK. 2001. 409–415.
|
| [10] |
李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述. 计算机应用, 2016, 36(9): 2508-2515, 2565. DOI:10.11772/j.issn.1001-9081.2016.09.2508 |
| [11] |
Zhang L, Yang M, Feng XC. Sparse representation or collaborative representation: Which helps face recognition? Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain. 2011. 471–478.
|
| [12] |
关韵竹. 场景图片的文字定位算法研究[硕士学位论文]. 武汉: 武汉邮电科学研究院, 2017.
|
| [13] |
宋鹏飞. 基于LBP特征的人脸识别算法改进研究[硕士学位论文]. 沈阳: 东北大学, 2014.
|
| [14] |
张锟. 基于稀疏内积和时间分布计算的高效物体检测[硕士学位论文]. 天津: 天津大学, 2014.
|
| [15] |
赵汝哲, 房斌, 文静. 自适应加权LBP的单样本人脸识别方法. 计算机工程与应用, 2012, 48(31): 146-149. DOI:10.3778/j.issn.1002-8331.2012.31.032 |
| [16] |
卢官明, 石婉婉, 李霞, 等. 基于协作表示的人脸表情识别. 南京邮电大学学报(自然科学版), 2017, 37(2): 51-56. |
| [17] |
Yuan HL, Li XC, Xu FY, et al. A collaborative-competitive representation based classifier model. Neurocomputing, 2018, 275: 627-635. DOI:10.1016/j.neucom.2017.09.022 |
 2021, Vol. 30
2021, Vol. 30



