2. 海南电网有限责任公司 信息通信分公司, 海口 570203
2. Information and Communications Branch, Hainan Power Grid Co. Ltd., Haikou 570203, China
目前, 随着智能电网时代的来临, 对于配电网的要求也越来越高[1]. 配电网业务繁杂, 覆盖面广, 其通信组网的方式也多种多样, 主要包括无线通信、有线光纤网络、本地局域网络等, 因此需要一个合适的组网方式来满足整体需求. 终端设备数量大、分布不均、密度随各地条件不同而不能平衡, 都大大加剧了通信网络的复杂程度, 给系统运行维护提出了难题. 因此一个合格的配电通信网融合管理模型是十分必要的[2].
本文采用混合网络框架, 将无线网和有线网混合虚拟, 以电力线载波通信(Power Line Carrier communication, PLC)[3]和无线mesh网络(Wireless Mesh Network, WMN)[4]为例. 发挥各自的特点和优势来提高整个配电通信网络的性能. 建立目标函数模型, 最大限度的提高网络的业务吞吐能力, 提高性能, 采用粒子群算法设计和优化无线虚拟网络映射, 对新建立的模型进行仿真验证, 通过与遗传算法的比较, 证明了采用本文的算法具有明显的优势[5].
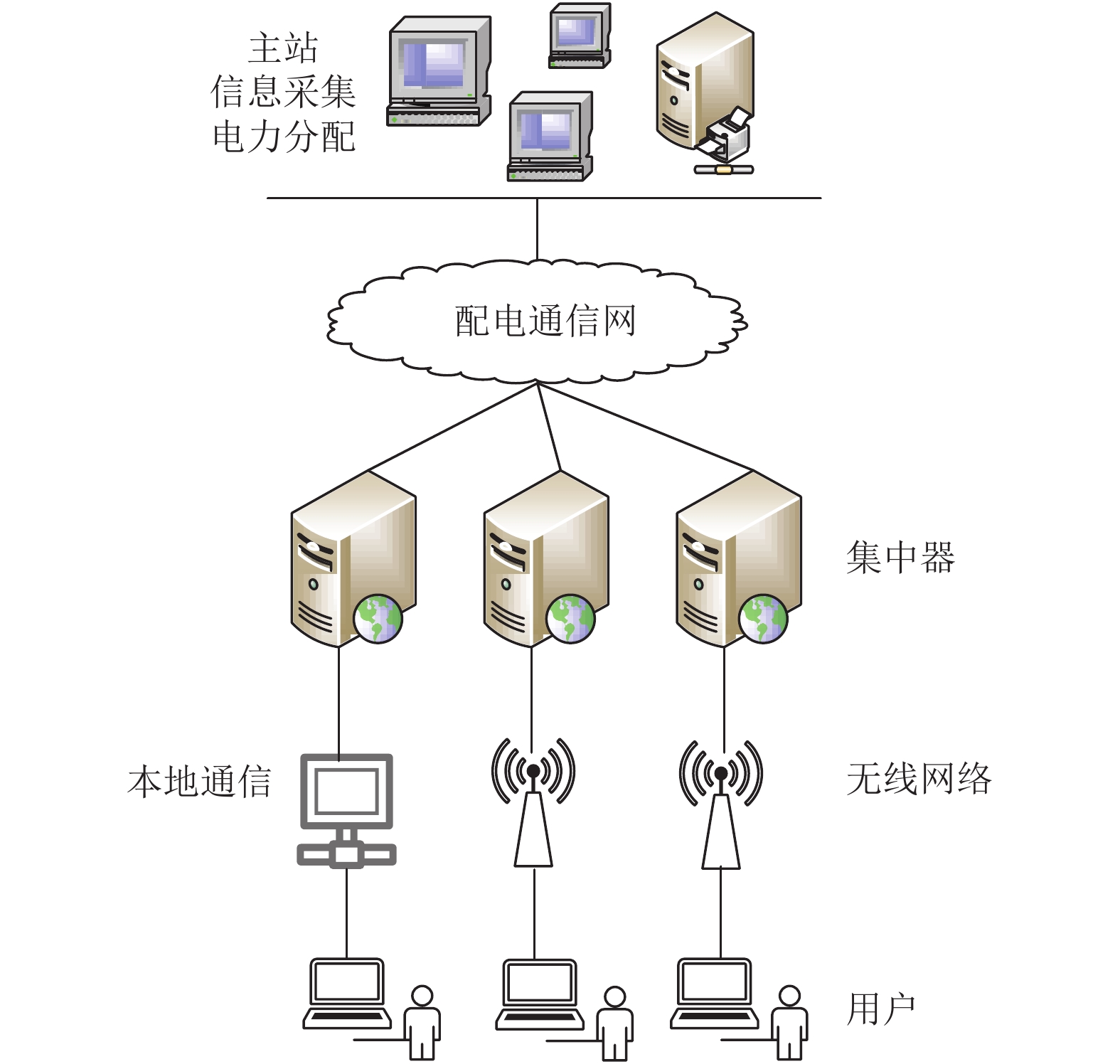
1 智能配电通信网混合网络模型 1.1 配电通信网模型配电通信网的业务主要包括用户信息采集、电力资源分配、负荷管理、故障监测等, 其模型如图1.
|
图 1 配电通信网模型 |
在当前的环境下, 各大网络的架设和安排基本成型, 如果对于现有网络进行重新定位和规划、架构不切实际, 而在原有网络结构的基础上, 进行资源优化整合, 达到提高配电网业务效率的目的, 是目前最行之有效的方法[6]. 网络虚拟化技术可以在不改变物理网络的情况下, 大幅提高原有网络的利用效率, 因此成为解决配电通信网络问题的一个重要解决手段和方法[7].
网络虚拟化在一个公用的物理网络上, 根据配电业务性质和要求的不同构建不同的虚拟网络, 虚拟网络独立运作, 根据需求调整资源配置, 能够有效提升服务水平、降低维护成本[8]. 由于配电网的形式多样, 使得虚拟网络中最主要的问题是网络映射, 如何根据多种类型的有线和无线网络构建有效的虚拟网络, 成为解决问题的关键[9].
1.2 混合网络虚拟化网络虚拟化通过提供虚拟网络, 允许多个网络相互独立工作, 从而允许在不改变现有物理网络的情况下, 为网络系统的构建和优化提供了可能和手段[10]. 在不同的网络需求情况下, 可以对实际情况进行调整, 改变网络结构的布局, 灵活运用网络优势, 提高服务质量, 给用户更好的业务感受, 满足了智能电网业务多样性的要求, 应用前景广阔[11].
网络虚拟化[12]技术中, 虚拟网络和物理网络相互独立, 也相互关联, 没有一一对应的需求, 可根据实际映射情况, 做灵活处理, 大大提高了网络的利用效率.
对于PLC网络和WMN网络来说, 各自具有各自的特点, 对于数据的传输速率也差别明显. 应用虚拟网络对其进行映射, 从而可以用来处理各种通信业务需求. 对于配电通信网中的主要业务可以分为控制操作和数据管理两大部分[13]. 根据各自的业务特点, 控制操作对于反馈意见的实时性要求高, 可以使用PLC网络进行处理, 而数据处理部分的工作量大, 对于网络要求较高, 需要使用WMN网络进行处理, 从而最大限度的提高整个网络业务的吞吐能力[14].
在不改变现有通信设备的前提下, 混合网络的虚拟化, 需要合适的映射方法来将虚拟资源和物理网 络对应, 并保证虚拟网络互相不干扰, 独自完成网络的任务安排[15]. 对于WMN网络, 可通过不同的子载波来描述不同业务的虚拟网络, 因此可以有效避免业务干扰.
1.3 虚拟网络映射问题模型配电通信网的资源映射问题是构建网络虚拟化的关键问题, 因此将实际情况进行数据化处理的方法选择成为其中的关键. 为了有效抽象化PLC和WMN网络, 使得网络处理能力得到最优化的效果, 需要将整个虚拟网络进行层级化处理, 从而构建底层网络模型, 虚拟请求模型和映射描述3个部分. 底层网络进行抽象化处理, 请求模型数字化处理实际业务中的控制操作和数据管理, 通过映射描述将整个问题进行抽象化, 达到最优化业务处理能力的目的.
(1)底层网络模型
在整个网络模型中, 利用无向的带权图GS(NS, ES)来描述底层网络结构, 分别使用GSp(NS, ESp)和GSw(NS, ESw)代表PLC网络和WMN网络. 由于通信网节点是固定不变的, 因此二者具有相同的节点集合Ns, 节点的数量可以定义为n, 每个节点包括两种状态, 即发射子载波和接受子载波, 其中第i个节点的发射子载波和接受子载波分别用ST(i)和SR(i)来表示. ESw和ESp分别代表了PLC网络和WMN网络的链路集合, 并用Rep来描述该链路的数据传输可靠性.
(2)虚拟请求模型
虚拟请求模型的构建与底层网络模型情况十分类似, 采用同样的方法, 构建Gv(Nv, Ev), Nv在这里主要用于描述网络中的虚拟节点, Ev对应的描述网络中的虚拟链路集合. 整个虚拟请求模型中根据实际业务工作情况, 主要包括3种状态, 分别为控制请求c(i)、操作请求o(i)和流量请求b(i).
控制请求和操作请求分别包含了消息报文的多种信息, 如报文长度、报文时间和可靠性等. 因此可以根据实际情况将控制和操作请求分别描述为c(i)=(Lc(i), Dc(i), Rc(i))和o(i)=(Lo(i), Do(i), Ro(i)). 由于网络带宽的限制, 需要通过传输概率Pc(i)和Po(i)来表示数据传输的效果. 采用fb(i)表示流量请求中经过映射后的实际流量部分, 可以用于整个网络的映射描述.
(3)映射描述
映射描述情况是指将虚拟网络上的请求反馈到PLC和WMN等物理网络上, 用g代表某种约束情况下的虚拟网络映射情况描述, 即:
| $ {{g:Gs(Ns,Es)}} \to {{Gv}}'{{(Nv,Ev)}} $ | (1) |
其中, Gv′是Gv的子集.
配电通信网中的设备均是固定的, 因此整个虚拟网络中的节点没有设备映射的问题. 从而可以采用多址接入技术, 对每个节点分配相应的子载波来满足不同的业务请求. 对于特定的PLC和WMN物理网络, 可以根据不同节点的业务请求, 构建子载波矩阵Tc(i, j)、To(i, j), 和Tb(i, j)来记录并完成网络的最优化, 保证整个网络具有最大的业务吞吐能力. 从而可以得到最大吞吐能力为:
| $\left\{ \begin{split} & \max :\sum\limits_{i = 1}^{n - 1} {{f_b}} (i) \\ & {\rm{s.t.}}\left\{ \begin{array}{l} {P_c}(i) \ge {R_c}(i) \\ {P_o}(i) \ge {R_o}(i) \\ b(i) \ge {f_b}(i) \\ \displaystyle\sum\limits_{i = 1}^{n - 1} {{T_c}} (i,j) + \displaystyle\sum\limits_{i = 1}^{n - 1} {{T_o}} (i,j) + \displaystyle\sum\limits_{i = 1}^{n - 1} {{T_b}} (i,j) \le S(i) \\ \end{array} \right. \\ \end{split}\right. $ | (2) |
其中, fb(i)为第i个节点映射后满足的流量大小, S(i)为子载波的总量. 由式(2)可知, 改虚拟网络的业务优化问题是典型的NP问题. 普通的优化算法由于计算复杂在这里并不适用, 遗传算法虽然能够降低复杂度, 但是很难找到全局最优解, 因此需要采用一种更优化的算法来降低上式的复杂程度, 本文采用了基于粒子群的算法来完成配电通信网虚拟化网络的最优解计算, 并证明其比有效性.
2 配电通信网的虚拟化算法 2.1 算法分析粒子群算法(Particle Swarm Optimization, PSO)是-种群体智能最优化求解的算法, 来源于鸟群对于食物的位置判断特性, 该算法适用于配电通信网络对于信息位置等的判断, 且求解方法简单, 调整参数少, 与其他算法相比, 数据优化方面的优势更为明显.
对现有的粒子群算法进行调整, 使其更适合于配电通信网, 其中的一些概念需要重新定义. 根据网络适用情况, 定义种群中粒子个体数量为M, 整个域内的最优化的解存在于D维的空间中. 定义粒子种群中的参数Xi(t), Vi(t), Pi(t). 分别代表位置、速度、最佳点. 种群的最佳位置点定义为Pg(t). 为了获得目标函数的最优化解, 其最佳位置可以定义为:
| ${P_i}(t) = \left\{ \begin{array}{l} {P_i}(t - 1),f({X_i}(t)) \ge f({P_i}(t - 1)) \\ {X_i}(t),f({X_i}(t)) \le f({P_i}(t - 1)) \\ \end{array} \right.$ | (3) |
| ${p_g}(t) = \arg \min [f({P_1}(t)),f({P_2}(t)),\cdots,f({P_M}(t))]$ | (4) |
其中, 初始点Pi(0) 的最佳位置为Xi(0), 适应度函数用f表示. 适应度函数的选取对于粒子的最优解选取至关重要, 直接决定了函数的收敛速度和求解过程. 改函数主要决定于目标函数, 对于配电通信网来说, 其最终的目标函数既是整个网络的业务吞吐能力, 即:
可以将适应度函数进行变形得:
| $f = a\left(\frac{{{R_c}}}{{{P_c}}} + \frac{{{R_o}}}{{{P_o}}} + \frac{{{f_b}}}{b}\right) + b\left(\frac{{{T_c} + {T_o} + {T_b}}}{S}\right)$ | (5) |
式(5)中, a, b为函数约束系数, S为子载波总量.
在配电通信网络中, 粒子的目的在于对于子载波进行分配调整, 其位置向量Xi(t)可以用矩阵Tc(i, j)、To(i, j), 和Tb(i, j)来表示. 速度向量Vi(t)对应子载波分配方式的调整, 从而可以得到:
速度:
| $\begin{split} {V_i}(t + 1) =& c \times g \times ({P_i}(t) - {X_i}(t)) + d \times h \times ({P_g}(t) - {X_g}(t)) \\ & + u \times {V_i}(t) \\ \end{split} \!\!\!\!\!\!\!\!\!\!\!\!\!$ | (6) |
位置:
| ${X_i}(t + 1) = {X_i}(t) + {V_i}(t + 1)$ | (7) |
其中, u, c和d为系统系数, g和h是两个小于1的正数.
2.2 算法设计对于本文涉及的配电通信网络中, 混合网络主要包括PLC和WMN两部分, 该网络的通信过程主要包括:
(1)计算PLC网络上资源利用情况, 得到实时数据的传输成功结果, 从而将剩余的资源分配给WMN网络, 用于子载波的计算调整;
(2)对剩余的网络资源, 按照粒子群算法的原理, 完成子载波分配实现整个网络调整的目的, 最终实现业务吞吐能力最强.
WMN网络的虚拟映射粒子群算法的实现过程包括有:
Step 1. 初始化实验环境, 根据条件分别设置M, u, c和d等实验参数;
Step 2. 初始化粒子群参数, 设定节点数量n和可用于分配的子载波数量k, 调整子载波分配, 使其与节点要求数据成比例;
Step 3. 判断适应度是否收敛, 对子载波的适应度函数进行求解, 得到满足粒子群算法映射的适应度;
Step 4. 根据得到的适应度函数和式(3)、式(4)对子载波分配方案进行优化管理;
Step 5. 根据式(5)、式(6)对子载波分配方案进行再次优化和调整;
Step 6. 重复上述步骤Step 3~Step 5, 直至迭代中止, 输出分配方案和吞吐量结果.
3 实验分析和讨论为了验证粒子群算法的有效性, 采用Matlab 2017对其进行验证, 并将仿真结果与遗传算法进行比较, 依次从计算时间、满意程度和吞吐能力几方面来证明本算法的优势.
设定仿真条件为: 整个网络中存在一个控制中心和10个网络节点, 每个节点均有一个发射终端和一个接收终端, 共128个子载波用于分配, 种群粒子数量为20个, 迭代上限设定为200次, 其他参数设定如表1所示.
| 表 1 仿真参数设定 |
(1)平均映射时间
分别利用Matlab对两种模型进行计算, 均计算100次后, 比较两种算法的平均映射时间见表2. 从表中可以看到, 从计算时间上看, 粒子群算法由于需要处理更多的信息数据, 计算量大, 因此其计算所需要的时间更长, 但是总体来说两者的区别并不明显.
| 表 2 平均映射时间对比 |
从计算复杂度来说, 粒子群算法的求解简单且需要调整的参数更少, 只是需要根据粒子分布情况来定义配电通信网中的子载波分配问题, 尽管存在些许延迟, 但是从映射时间的比较来看, 与其他算法的区别并不大, 不会影响整个电力系统的运行效率.
(2)满意程度
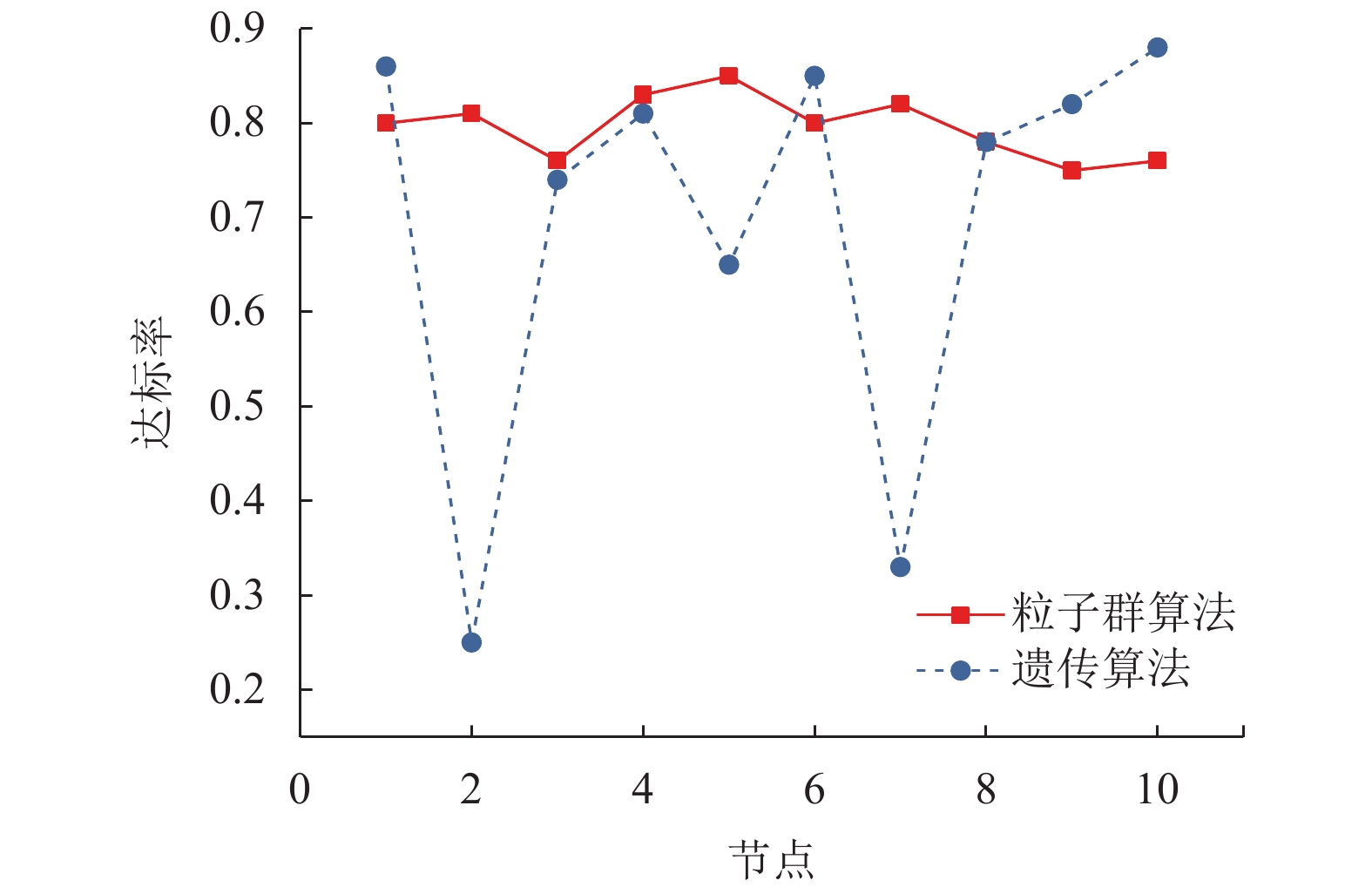
设定数据传输速率达到15 Mb/s时为传输目标速率, 将各个节点的实际速率与目标速率进行比较, 得到算法在整个网络中的数据达标率情况, 从图2中可以看出, 粒子算法的数据达标率很高, 均超过75%, 对比遗传算法, 虽然其有部分节点数据达标率超过88%, 但有个别节点传输数据极低, 不满足资源分配优化的目的, 从而证明在资源分配方面粒子算法具有明显优势.
|
图 2 传输达标率比较 |
(3)最大业务吞吐量
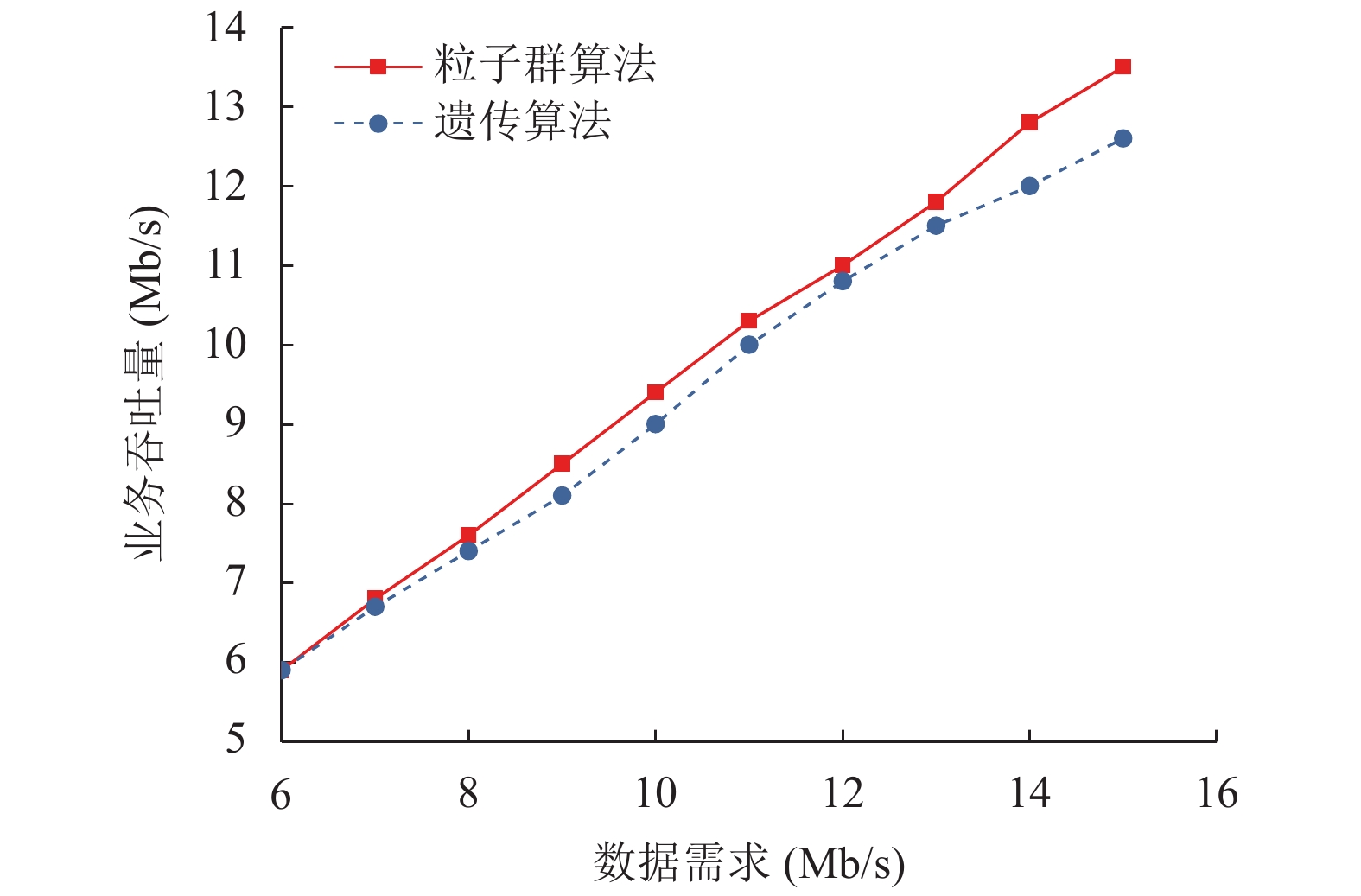
图3显示了两种算法的吞吐能力对比情况, 在混合网络的情况下, 虚拟化映射后的结果可以看到, 粒子群算法大大强于遗传算法, 传输数据速率要求越高的情况下, 优势越明显.
|
图 3 最大业务吞吐量对比 |
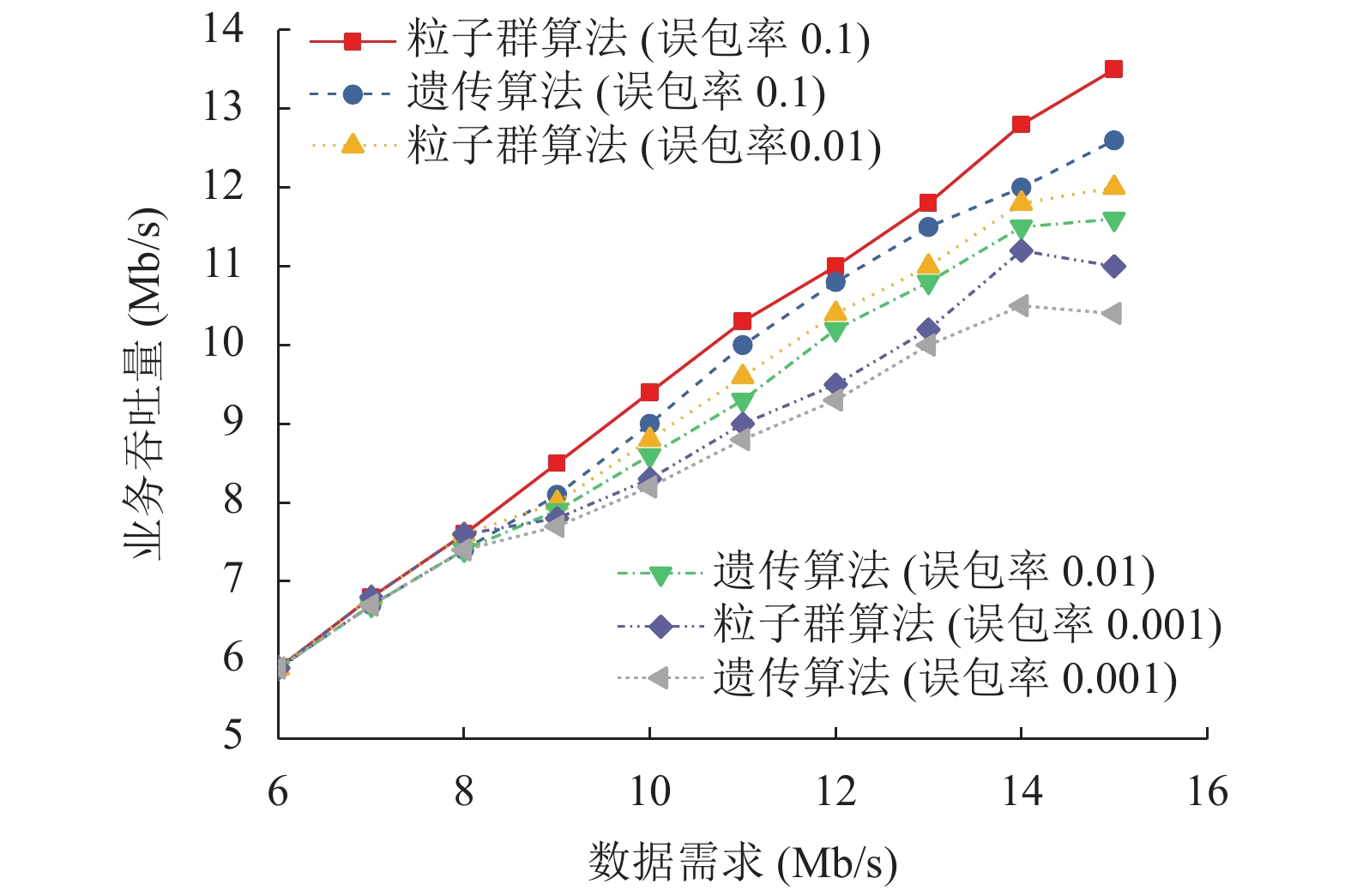
为了更清楚的比较两个模型的效果, 改变混合网络中PLC网络的误包率, 进一步比较最大业务吞吐量如图4所示. 图中可以看到随着误包率的下降, 两个模型的吞吐能力都在增强, 主要是由于误包率越高, 需要分配给可靠性部分的子载波部分就会越大, 从而造成用于吞吐量部分就会变少. 但是图中同样可以比较出, 在相同的误包率情况下, 粒子模型的吞吐量还是要大于遗传算法, 数据需求越大时, 差别越明显.
|
图 4 误包率对于业务吞吐量的影响 |
改变操控可靠性的需求量, 进一步比较业务吞吐量的区别. 如图5所示, 可以看出, 当操控需求增大时, 其变化过程与误包率结果类似, 两个模型的业务吞吐量都会逐渐降低. 其原因同样是由于较多的子载波被安排给操控可靠性, 因此用于吞吐量的部分被减弱.
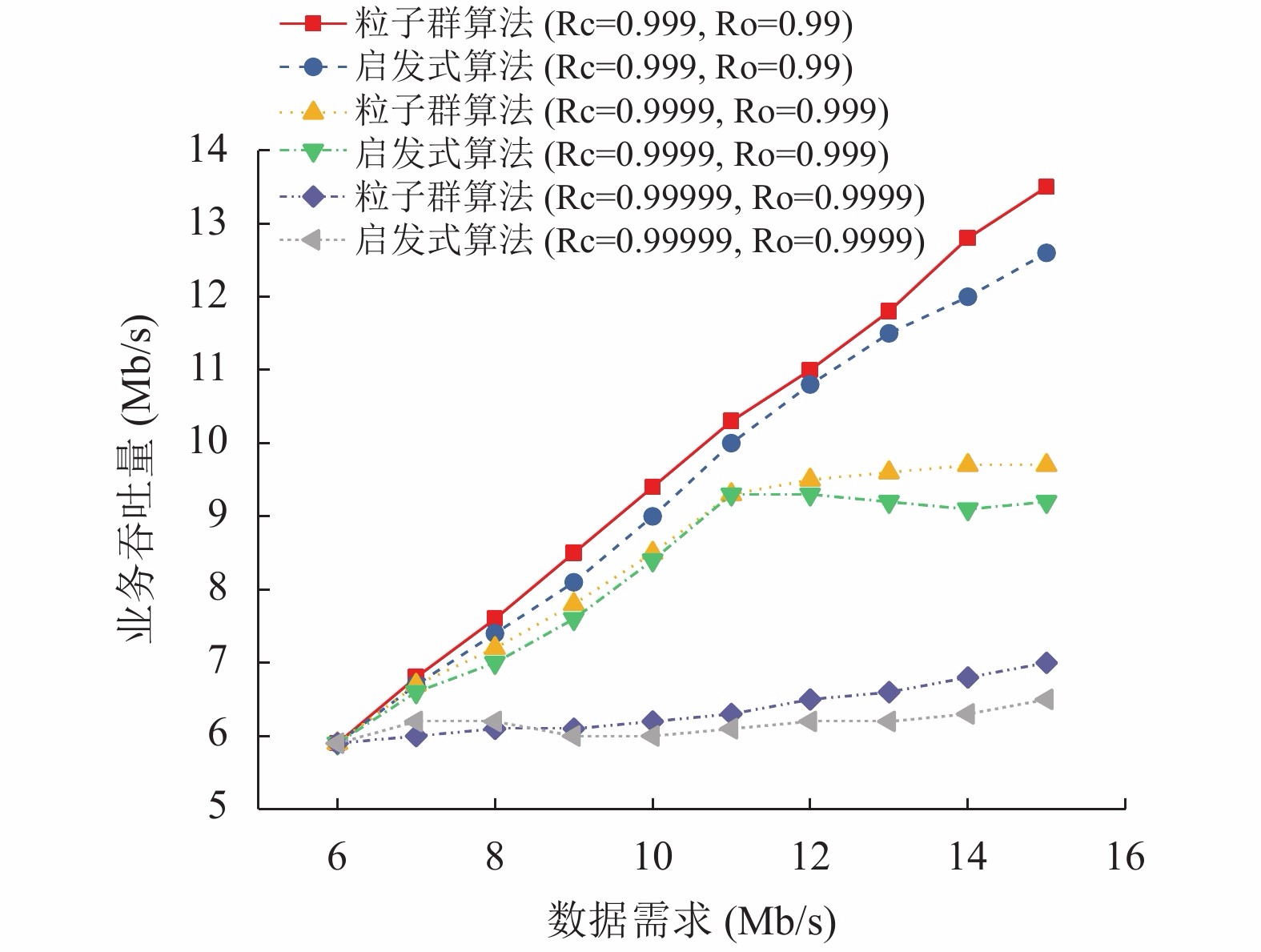
|
图 5 可靠性需求对于业务吞吐量的影响 |
粒子群算法是通过在迭代过程中不断比较局部与全局最优解的关系, 从而得到任务吞吐量的极大值. 为了比较迭代次数对于计算准确度的影响, 利用Rastrigin函数对本文算法进行测试, 计算结果如图6所示, 图中可以看出粒子群算法的收敛速度较快, 当迭代次数低于200次是, 其计算准确度已经能够达到准确度100%, 获得全局最优解的情况, 得到最大的任务吞吐量.

|
图 6 迭代次数对于准确度的影响 |
改变本文的测试条件, 将网络节点数量由10个增加到20个, 种群数量由10个变为20个, 得到迭次数与计算准确程度的关系, 如图7所示, 从中可知, 为了得到该种情况下的全局最优解, 需要将迭代次数更新为600次. 对于工作条件更复杂的情况, 需要通过增大迭代次数等条件, 获得全局最优解.
但从结果的比较来看, 各种情况的粒子群算法都是优于遗传算法的, 进一步证明粒子群算法更适合用于配电通信网络.
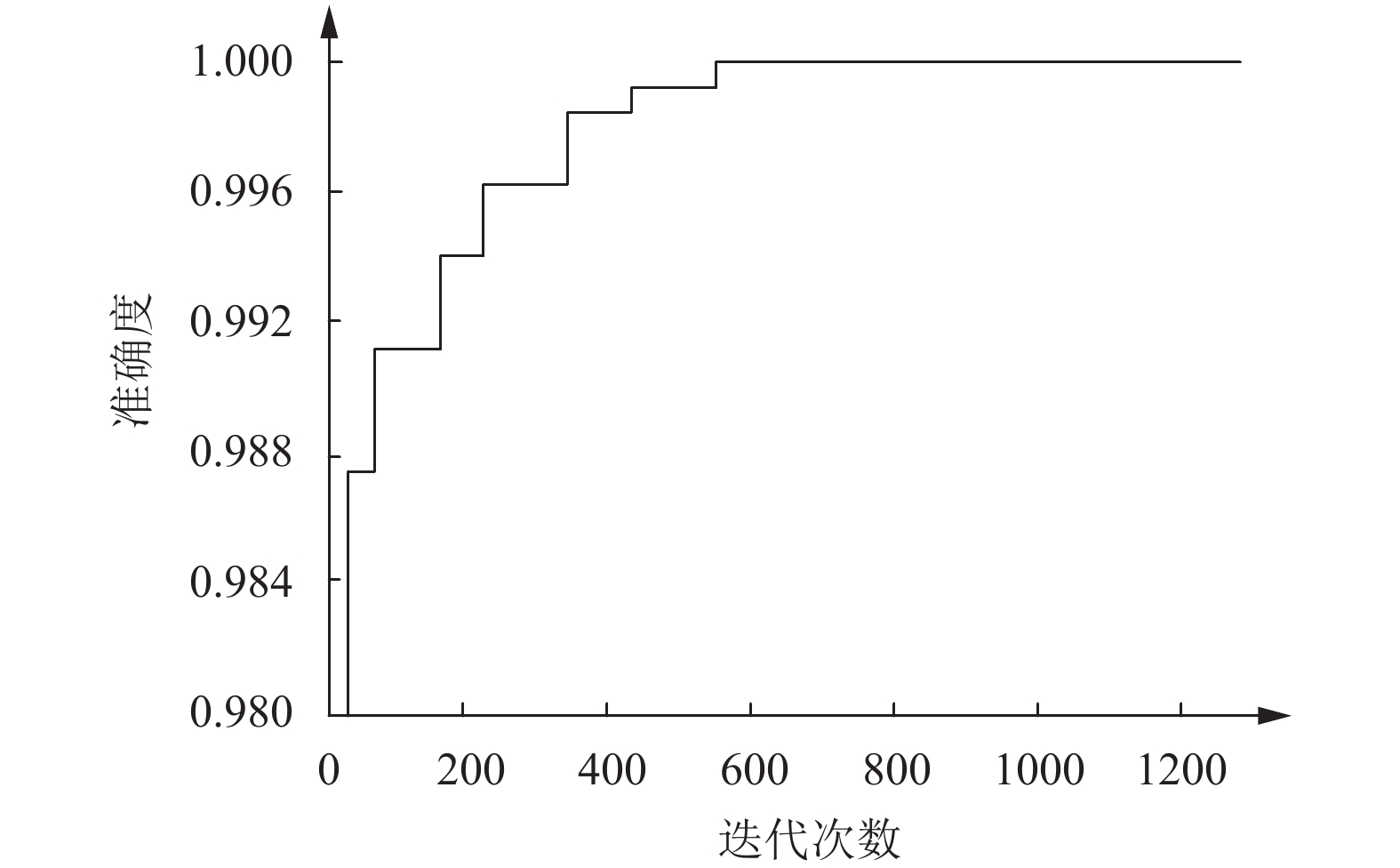
|
图 7 改变条件后的迭代次数与准确度的关系 |
4 结束语
为了解决配电通信网中各种网络信息融合的问题, 本文建立了基于粒子群算法的混合网络的资源映射模型. 将WMN和PLC两个不同类型的网络映射到同一个物理网络上, 根据PLC网络和WMN网络的特点, 对其安排不同的工作任务, 发挥各自网络的优势和特点, 将更多的子载波用于业务吞吐上, 从而大大提高该模型的业务吞吐量.
将该数据处理算法与遗传算法进行对比, 并在多种情况下反复验证, 证明了该模型更适合于配电通信网络. 从仿真结果可以看到, 本模型所采用的粒子群算法尽管评价映射时间较遗传算法大些, 但是其数据处理结果更合理, 业务吞吐量大, 服务效果更好, 各节点的公平性更高, 证明其搜索的范围更广, 结果更合理, 为配电通信网融合管理模型的建立提供了新的思路.
| [1] |
李勇, 陈雨, 蔡晔, 等. 基于信息物理接口矩阵的IEC61850变电站自动化系统可靠性分析. 电力自动化设备, 2019, 39(1): 84-90, 98. |
| [2] |
余娟, 杨燕, 杨知方, 等. 基于深度学习的概率能量流快速计算方法. 中国电机工程学报, 2019, 39(1): 22-30. |
| [3] |
潘旭, 王金丽, 赵晓龙, 等. 智能配电网多维数据质量评价方法. 中国电机工程学报, 2018, 38(5): 1375-1384. |
| [4] |
Arani MFM, Mohamed YARI. Analysis and performance enhancement of vector-controlled VSC in HVDC links connected to very weak grids. IEEE Transactions on Power Systems, 2017, 32(1): 684-693. DOI:10.1109/TPWRS.2016.2540959 |
| [5] |
郭苑灵, 林天池, 梁开根. 面向通信与计算协同的配电通信网效能评价方法研究. 电气时代, 2018(12): 81-82. |
| [6] |
王宁. EPON配电通信网故障定位与排查. 设备管理与维修, 2019(1): 164-165. |
| [7] |
常海娇, 李信, 邢宁哲, 等. LTE-PON混合部署下的配电通信网数据接入点规划. 控制工程, 2019, 26(7): 1341-1347. |
| [8] |
李莉, 朱正甲, 任赟, 等. 基于绿色无线网络覆盖最优的配电通信网规划方法研究. 电力系统保护与控制, 2018, 46(7): 56-62. DOI:10.7667/PSPC170374 |
| [9] |
梁柱洪, 丁鹏, 刘元泼. 基于被动和主动测量的配电通信网网络质量监视. 电气时代, 2018(12): 79-80. |
| [10] |
陈永红, 李建岐, 白杰, 等. 终端通信接入网建设和运行模式探讨. 供用电, 2018, 35(3): 32-36. |
| [11] |
杨晓. EPON配电通信网络规划技术分析. 通信电源技术, 2018, 35(7): 277-279. |
| [12] |
林泽兵. 基于工业以太网的配电通信网接入层规模研究. 中国新通信, 2019, 21(20): 40-41. |
| [13] |
郑浩楠. 基于OCSVM的配电通信网流量异常检测研究. 信息通信, 2018(10): 97-98. DOI:10.3969/j.issn.1673-1131.2018.10.047 |
| [14] |
林密, 李博, 何书毅, 等. 基于扁平化管理模式的配电通信网管理及运维模式. 微型电脑应用, 2020, 36(4): 146-149. DOI:10.3969/j.issn.1007-757X.2020.04.046 |
| [15] |
陈钊渊, 黄良毅, 张铁刚, 等. 基于特征流量分析的配电通信网数据侵入研究. 电气自动化, 2019, 41(2): 53-55. DOI:10.3969/j.issn.1000-3886.2019.02.016 |
 2021, Vol. 30
2021, Vol. 30



