基于高阶变异的多错误定位实证研究

引用本文

娄琨, 尚颖, 王海峰. 基于高阶变异的多错误定位实证研究. 计算机系统应用, 2021, 30(5): 47-58.http://www.c-s-a.org.cn/1003-3254/7942.html

Lou K, Shang Y, Wang HF. Empirical Study on Higher Order Mutation-Based Multiple Fault Localization. Computer Systems and Applications, 2021, 30(5): 47-58(in Chinese).http://www.c-s-a.org.cn/1003-3254/7942.html

基于高阶变异的多错误定位实证研究

娄琨, 尚颖, 王海峰

北京化工大学信息科学与技术学院, 北京 100029

收稿日期：2020-09-26; 修改日期：2020-10-21; 采用时间：2020-11-12; csa 在线出版时间：2021-04-28

基金项目：国家自然科学基金(62077003, 61902015)

通讯作者：尚颖, E-mail: shangy@mail.buct.edu.cn.

摘要：错误定位是软件调试中最昂贵的活动之一. 基于变异的错误定位(MBFL)技术假定被大多数失败测试用例杀死的变异体能够很好地定位错误的位置. 之前的研究表明MBFL在单错误定位上有很好的定位效果, 但关于MBFL在多错误定位上的表现没有被深入研究过. 近年来, 高阶变异体被提出用于构造难以被杀死的复杂错误, 但高阶变异体是否能提升MBFL的错误定位精度是未知的. 本文中, 我们研究了一阶变异体和高阶变异体在多错误定位场景下的表现. 进一步, 我们依据不同的变异位置将高阶变异体划分成3类: 准确高阶变异体、部分准确高阶变异体和不准确高阶变异体. 探索哪类变异体在错误定位上更有效. 基于5个程序上的实证研究, 我们发现在多错误定位场景下, 高阶变异体比一阶变异体有更好的定位效果. 更进一步, 我们发现不同种类的高阶变异体的影响是不容忽视的. 具体而言, 准确高阶变异体比不准确高阶变异体有更高的贡献. 因此研究人员应提出更有效的方法生成这类变异体用于未来的MBFL研究.

关键词: 错误定位基于变异的错误定位一阶变异体高阶变异体

Empirical Study on Higher Order Mutation-Based Multiple Fault Localization

LOU Kun, SHANG Ying, WANG Hai-Feng

College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China

Foundation item: National Natural Science Foundation of China (62077003, 61902015)

Abstract: Fault localization is one of the most expensive activities in software debugging.The Mutation-Based Fault Localization (MBFL) assumes that the mutants killed by most of the failed test cases can provide a good indication about the location of a fault. Previous studies showed MBFL could achieve desired results in a Single Fault Localization Scenario (SFL-Scenario), but its performance in a Multiple Fault Localization Scenario (MFL-Scenario) has not been thoroughly evaluated. Recently, Higher Order Mutants (HOMs) have been proposed to model complex faults that are hard to kill, but whether HOMs can improve the performance of MBFL is still unknown. In this study, we investigate the impact of First Order Mutants (FOMs) and HOMs on MBFL in an MFL-Scenario. Moreover, we divide HOMs into three groups, i.e., accurate, partially accurate, and inaccurate HOMs, considering the mutation location in the program, to find which type of HOMs is more efficient in fault localization. Based on the empirical results on five real-world projects, we find that in an MFL-Scenario, HOMs can behave better than FOMs. The influence of the types of HOMs on the effectiveness of MBFL cannot be ignored. In particular, accurate HOMs can contribute more than inaccurate ones. Therefore, researchers should propose effective methods to generate this type of HOMs for future MBFL studies.

Key words: Mutantion Based Fault Localization (MBFL) mutation testing First-Order-Mutants (FOMs) Higher-Order-Mutants (HOMs)

1 引言

错误定位是识别程序执行过程中导致程序失败的元素的过程^[1]. 在软件调试的众多活动中, 错误定位是其中最复杂耗时的活动之一, 尤其在大规模复杂程序中. 为了减小定位错误位置的人工成本, 研究人员提出了众多错误定位方法, 例如基于切片的方法^[2], 基于频谱的方法^[3,4], 基于变异的方法等^[5].

在众多自动化错误定位方法中, 基于频谱的错误定位(Spectrum-Based Fault Localization, SBFL)方法^[3,4,6]是一种被广泛应用的方法. SBFL考虑到程序元素的二元覆盖矩阵, 但局限于其错误定位精度不高. 目前的研究显示基于变异的错误定位方法比最新的基于频谱的方法有更高的错误定位精度^[7,8]. MBFL是一种基于变异测试^[7]的方法^[9]. 截止目前, MBFL分为两种技术: Metallaxis-FL^[5]和MUSE^[9]. 研究表明^[10,11], Metallaxis-FL的错误定位效率和效果都要优于MUSE, 因此本文选择Metallaxis-FL作为MBFL原始方法.

在MBFL中, 将一个程序p通过简单的语法变化生成一系列错误程序p'(也就是变异体), 生成变异体的规则被称为变异算子. 根据变异算子使用的次数, 变异体可以分成两类: 一阶变异体(First-Order-Mutants, FOMs)和高阶变异体(Higher-Order-Mutants, HOMs), 其中FOMs是只使用一次变异算子生成, HOMs则是通过多次使用变异算子生成^[12].

在之前的MBFL研究中, 只有FOMs用于定位单错误程序^[5,13]. 但Xue等^[14]发现定位多错误更有困难, 耗时且成本巨大, 同时多错误之间存在错误干扰现象, 导致现有错误定位技术的定位效果较差. 另一方面, Offutt等^[15]发现杀死HOMs是否能检测出复杂错误是不确定的. 为填补这项研究内容, 我们进行了一项大规模的实证研究, 研究HOMs是否能提升错误定位的精度, 同时分析不同类别的HOMs与多错误之间的关系.

本文中, 我们着力研究FOMs和HOMs在多错误上的表现. 然后我们将HOMs分成三类研究不同HOMs分类的错误定位效果. 在我们的实验设置中, 首先应用Agrawal等^[16]提出的变异算子生成FOMs, 然后根据FOMs构建HOMs. 特别地, 针对多错误定位场景, 我们组合63个单错误程序生成100个多错误程序, 错误个数从2个至5个. 最后, 我们将HOMs分成3类用于比较不同类别HOMs的表现.

2 背景与动机 2.1 基于变异的错误定位技术

基于变异的错误定位技术是一种基于变异分析^[8]的错误定位方法. 变异分析通过对被测程序进行简单的语义改变, 生成与原始程序不同的版本. 这些人为植入错误的程序被称为变异体. 生成变异体的规则被称为变异算子. 本文采用Agrawal等^[16]提出的C语言的变异算子.

在变异分析中, 依据变异体和原始程序不同的输出, 使用变异体来评估测试用例的质量. 如果一个测试用例的执行结果不同于原始程序的结果, 那么这个变异体就被杀死, 记为killed或detected, 反之称这些变异体没有被杀死, 即not killed或live.

传统基于变异的错误定位技术主要包含以下4个步骤:

(1)获得失败测试用例覆盖的语句: 将测试用例T执行被测程序P, 获得覆盖信息和执行结果(pass或fail). 然后测试用例就可以区分为通过测试用例集合T_p和失败测试用例集合T_f. 被失败测试用例覆盖的语句集合记为cov_f.

(2)生成和执行变异体: 采用不同变异算子, 对失败测试用例覆盖的语句植入错误生成变异体. 对某一条语句s生成的变异体集合记为M(s). 然后将所有测试用例执行某一个变异体m, 依据执行结果, T_k(m)为杀死变异体m的测试用例集合, T_n(m)为未杀死变异体m的测试用例集合.

(3)计算程序语句怀疑度: 变异体的怀疑度可以用不同的MBFL公式计算得到, 这些公式都基于以下4个参数: a_np=|T_n∩T_p|, a_kp=|T_k∩T_p|, a_nf=|T_n∩T_f|, a_kf =|T_k∩T_f|. 其中, a_np表示通过测试用例中未杀死变异体的数量, a_kp表示通过测试用例中杀死变异体的数量, a_nf表示失败测试用例中未杀死变异体的数量, a_kf表示失败测试用例中杀死变异体的数量. 表1列举了3个研究人员常用的怀疑度计算公式(Ochiai^[17], Tarantula^[18], Dstar ^[19]). 本文的实验中使用Ochiai作为MBFL公式, 因为其在MBFL研究中被广泛使用^[5,9], 且效果好于其他公式^[13]. 计算完变异体的怀疑度, 将某条语句对应的变异体集合的怀疑度最大值赋值为该条语句的怀疑度.

(4)生成错误定位报告: 依据程序语句的怀疑度大小, 降序排列生成程序语句排名表. 开发人员可以根据排名表从上至下查找并修正程序错误.

表 1 常用怀疑度公式

基于上述过程的描述, 我们可以发现MBFL是基于“大部分失败测试用例杀死的变异体与程序错误有关”假设的研究工作, 其理论基础是基于以下两类假设^[20]: (1)将变异体视为是原被测程序的一种潜在修复; (2)将变异体视为原被测错误程序的近似版本. 变异体执行测试用例后的状态有两种: 杀死(killed)和未杀死(not killed). 其中, 杀死状态分为: 被失败测试用例杀死(a_kf)和被通过测试用例杀死(a_kp). 在被失败测试用例杀死的变异体, 存在两种情况: (1)变异体的状态从失败变成通过, 即程序被修复; (2)变异体仍然为失败, 但输出与原始程序不同. 这两种情况都有助于揭示错误位置, 第一种程序修复的情况, 可以依据变异的位置来确定程序错误的位置. 第二种情况, 变异体的输出与原始程序不同, 其有可能是对错误位置变异而造成的输出不同, 此变异体的行为特征与错误程序更加相似. 另一方面, 被通过测试用例杀死的变异体, 其更可能是对正确语句进行变异, 造成输出与原始程序不同. 并且, Moon等^[9]的研究发现, 错误语句生成的变异体在失败测试用例下更容易通过, 而正确语句生成的变异体在通过测试用例下更容易失败.

同时, 从表1变异体怀疑度公式中可以看出, 变异体的怀疑度值与a_kf呈正相关关系, 与a_kp呈负相关关系. 本文通过计算变异体m在测试用例上a_kf与a_kp的差值来度量该变异体对错误定位的影响程度, 即贡献度C(Contribution):

$ C\left( {T,P,m} \right) = {a_{kf}} - {a_{kp}} $

(1)

其中, T表示测试用例集, P表示被测程序. C(T, P, m)越高表示该变异体的贡献度越高.

同理, 对变异体集合M的平均贡献度AC(Average Contribution)的计算公式为:

$ AC\left( {T,P,M} \right) = \frac{{\displaystyle\sum\limits_i^{\left| M \right|} {C\left( {T,P,{m_i}} \right)} }}{{\left| M \right|}} $

(2)

其中, |M|表示集合中变异体的数量.

目前研究人员对FOMs和HOMs之间的关系进行了研究. 如Gopinath等^[21]的研究表明许多HOMs与它们组成的FOMs在语义上是不同的. 然而, Langdon等^[22]的研究表明被测试用例杀死的HOMs数量高于杀死FOMs的数量, 因此HOMs相对于FOMs, 更容易被测试用例检出.

在早期的研究中, Offutt等^[15]指出: 杀死n阶变异体是否意味着我们可以检出复杂错误还有待确定. 为了回答这个问题, 我们是第一个进行关于比较FOMs和HOMs在定位程序错误上的控制实验的.

2.2 研究动机

在先前的研究中, 大部分MBFL技术基于单错误假设^[5,9,13,23]. 然而, 实证研究表明^[24], 单个程序失败往往是由系统中的多个故障触发的. Digiuseppe和Jones发现, 多个错误对错误定位的精度有负面影响^[25].

此外, Offutt的研究结果认为, 杀死n阶变异体是否可以检测到复杂的错误还有待确定^[15]. 在Debory和Wong的研究中^[26], 他们发现他们所提出的策略不能修复同一个程序中的多个错误, 是因为他们只考虑了FOMs. 换句话说, 采用HOMs来定位或修复程序中的多个缺陷是一种潜在可行的方法. 因此, 本文主要通过实证研究HOMs在单错误和多错误程序上的定位效果, 并分析多错误与HOMs之间的关系.

(1) HOMs分类

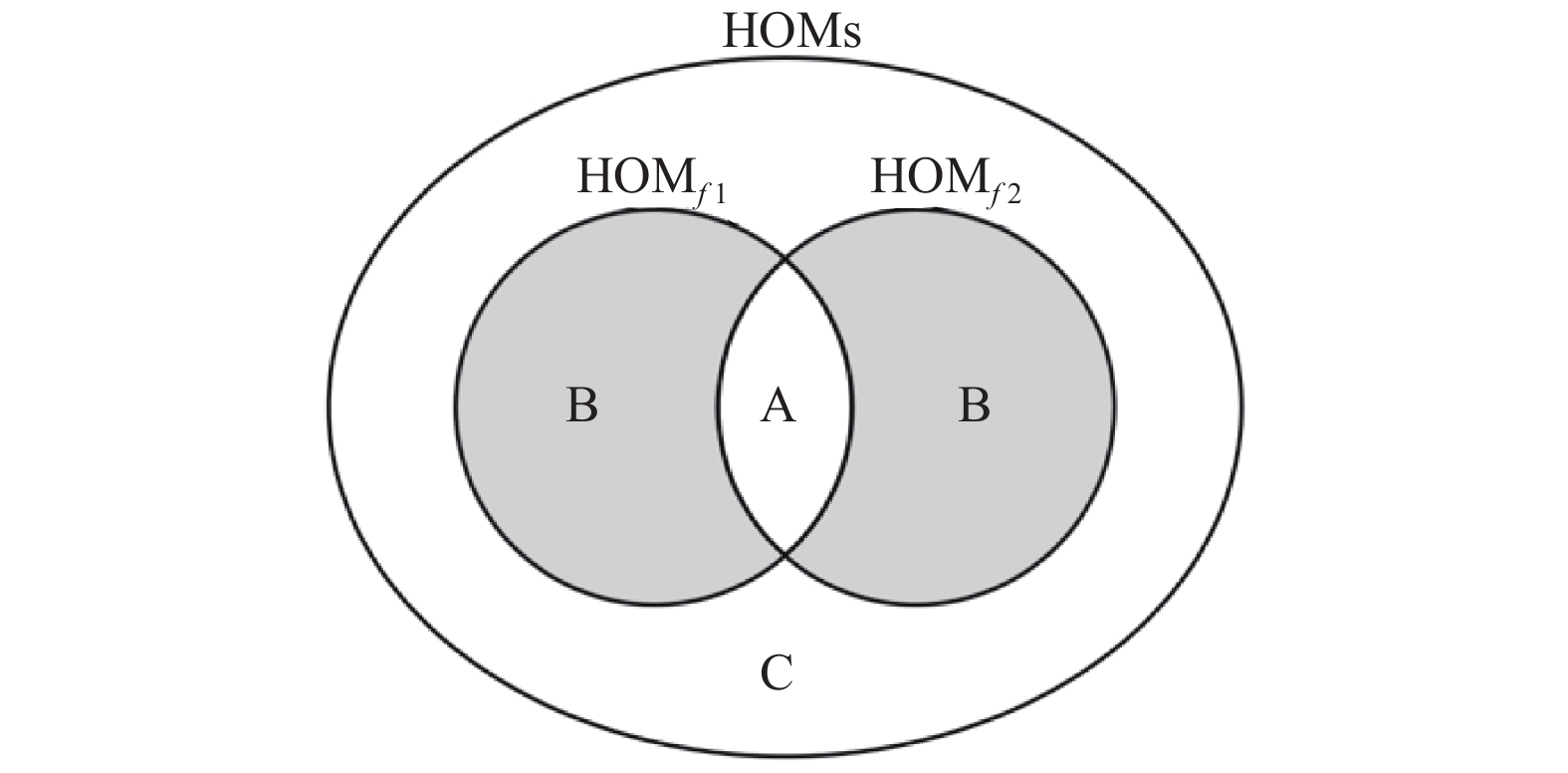
依据变异体在程序中的不同变异位置, 我们将HOMs分成3类. 为便于理解这3类变异体, 我们采用带有两个错误(f1和f2)的程序p作为例子. 首先, 我们HOM_f1为变异了错误语句f1的HOMs集合且HOM_f1∈HOMs; HOM_f2变异了错误语句f2的HOMs集合且HOM_f2∈HOMs.

其次, 如图1所示, 我们将HOMs分为以下3类:

类A: 准确高阶变异体(Accurate HOMs). 即, 同时在错误语句f1和f2上变异生成的HOMs. (HOM_f1∩HOM_f2).

类B: 部分准确高阶变异体(Partially accurate HOMs). 即, 只在错误语句f1或f2上变异生成的HOMs. (HOM_f1\HOM_f2)∪(HOM_f2\HOM_f1)

类C: 不准确高阶变异体(Inaccurate HOMs). 即, 在其他语句上变异生成的HOMs. (HOMs\(HOM_f1∪HOM_f2)

上述3种HOMs反映出不同HOMs的生成方法. 我们推测这3类HOMs在错误定位上有不同的表现. 基于这种推测, 我们进行了一次大规模的实证研究来分析3类HOMs的特性.

(2) MBFL例子

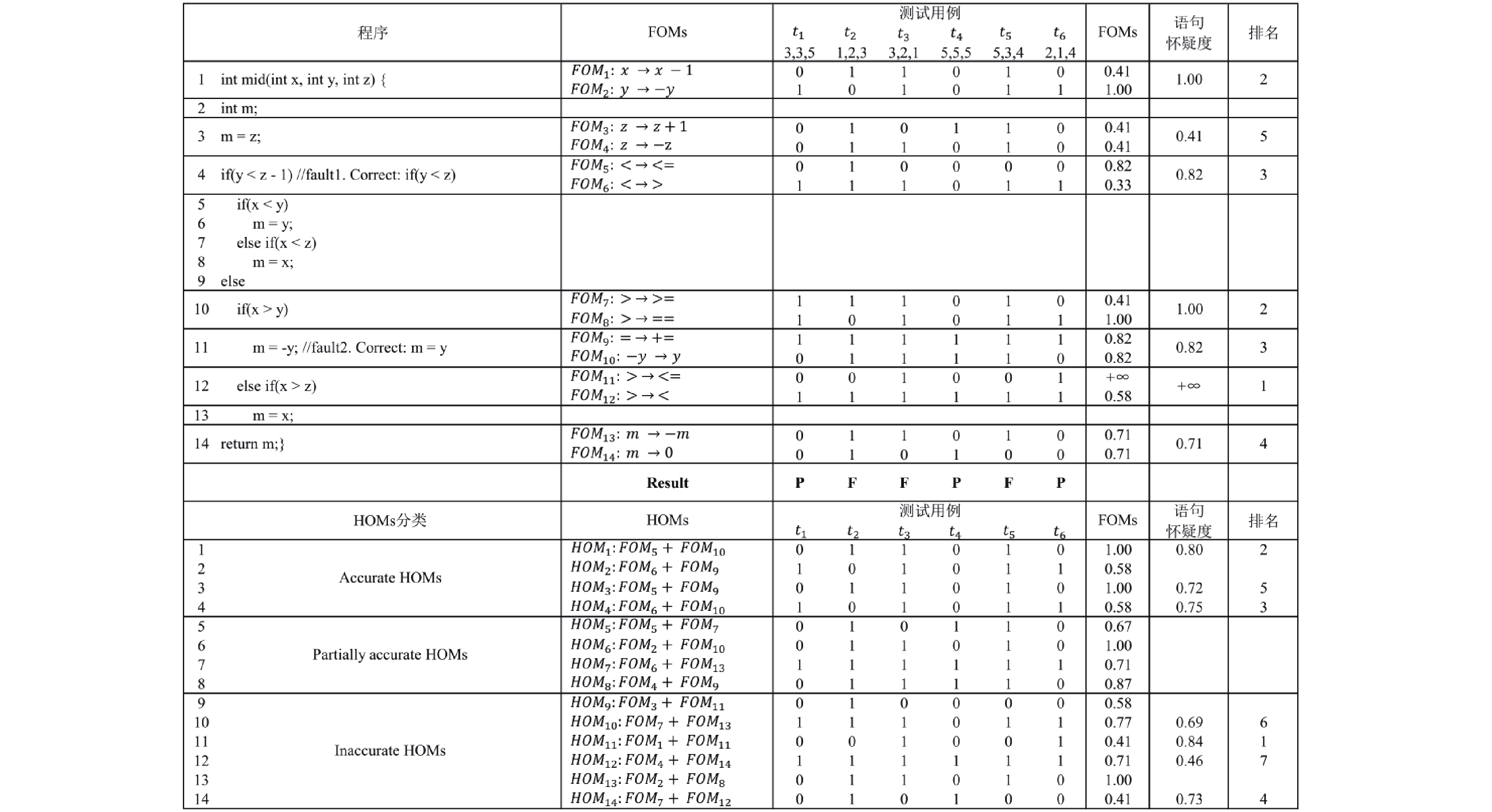
为进一步说明我们的研究动机, 我们使用图2中的例子来说明FOMs和HOMs如何在MBFL上使用.

在图 2中, 从左到右, 第1列为被测程序的源代码, 其中语句s₄和s₁₁为错误语句. 第2列为对应语句生成的变异体集合, 第3列划分为6部分, 分别是6个测试用例在变异体上的执行信息, 其中“1”表示测试用例杀死对应的变异体, “0”表示测试用例没有杀死对应的变异体, 第4和第5列表示计算得到的变异体怀疑度和语句怀疑度, 最后一列表示对应语句的排名. 在这个例子中, 每一个变异体的怀疑度都是用Ochiai公式计算的. 在图2中有两个给出的结果, 一个是FOMs的结果, 另一个是HOMs的结果.

图 1 HOMs分类

图 2 MBFL例子

使用FOMs进行错误定位. 假设MBFL技术在失败测试用例覆盖的每条语句只生成两个变异体, 该程序下共生成14个FOMs(列“FOMs”所示). MBFL首先利用测试用例的杀死信息计算FOMs的怀疑度(列“FOMs怀疑度”所示). 接下来, 同一语句生成的变异体中, 取最大的怀疑度记为该语句的怀疑度. 最后, 在“排名”列中, MBFL将错误语句s₄和s₁₁都排在第3位.

使用HOMs进行错误定位. 我们首先利用来自不同语句的两个FOMs构造HOMs, 最后生成3类共14条HOMs(列“HOMs”所示). 计算得到的HOMs怀疑度如列“HOMs怀疑度”所示. 接着, 为保证公平性, 我们通过计算语句相关HOMs怀疑度的均值作为该语句的怀疑度. 以语句s₁为例子, 与s₁相关的HOMs有3个(HOM₆, HOM₁₁和HOM₁₃), 其对应的怀疑度分别为1.00, 0.41, 和1.00.因此, 计算得到的语句s₁的怀疑度为Sus(s₁)=(1.00+0.41+1.00)/3=0.80.最终, 使用HOMs计算得到的语句怀疑度如列“语句怀疑度”所示. 最终, HOMs将错误语句s₄和s₁₁分别排在第3名和第2名.

基于上述的例子, 我们可以发现FOMs将两条错误语句排在前五名, 然而HOMs将错误语句排在前三名, 表明HOMs在这个例子中有更好的错误定位效果. 更进一步, 在高阶变异错误定位中, 三类变异体对错误定位有不同的贡献, 结合式(2), 准确HOMs的平均贡献度为:

$ AC(T,P,Accurate) \!=\! \frac{{\displaystyle\sum\limits_i^{{{|Accurate|}}} {C(T,P,{m_i})} }}{{{{|Accurate|}}}} \!=\! \frac{{3 + 0 + 3 + 0}}{4} \!=\! 1.5 $

(3)

部分准确HOMs的平均贡献度为:

$ \begin{split} AC(T,P,Part - accurate) =& \frac{{\displaystyle\sum\limits_i^{{\rm{|}}Part - accurate{\rm{|}}} {C(T,P,{m_i})} }}{{|Part - accurate|}} \\ =& \frac{{1 + 3 + 0 + 2}}{4} = 1.5 \end{split} $

(4)

不准确HOMs的平均贡献度为：

$ \begin{split} AC(T,P,Inaccurate) =& \frac{{\displaystyle\sum\limits_i^{|Inaccurate|} {C(T,P,{m_i})} }}{{|Inaccurate|}} \\ =& \frac{{1 + 1 + 0 + 0 + 3 + 0}}{6} = 0.83 \end{split} $

(5)

从以上结果可以看出, 准确HOMs的平均贡献度等于部分准确HOMs, 不准确HOMs的平均贡献度最低. 据我们所知, 本文首次研究FOMs和HOMs在多错误程序上的定位效果. 更进一步, 我们研究了三类HOMs的错误定位效果并分析其差异.

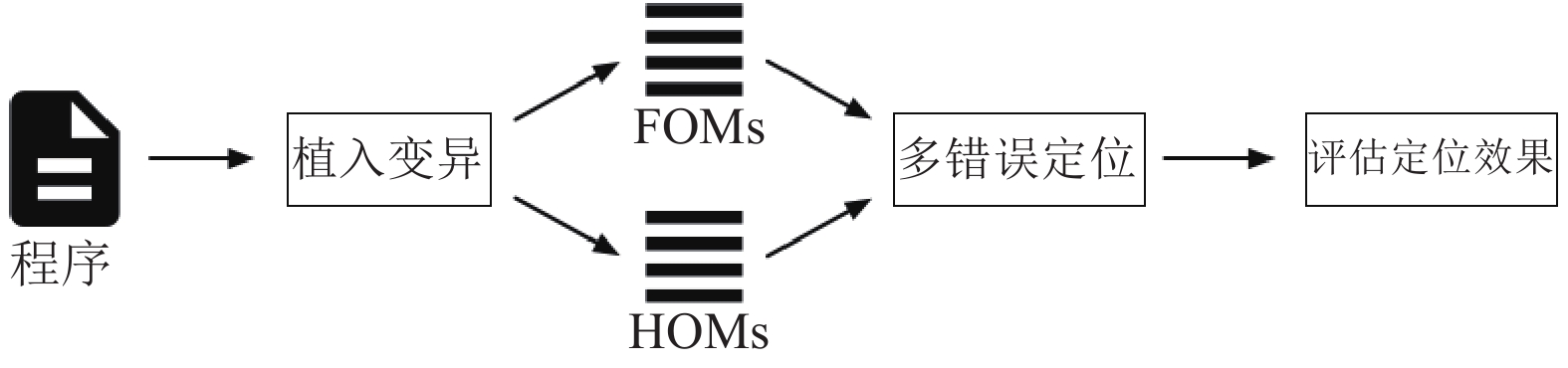
3 实验设计

本章讨论实验中使用的程序和实验设计流程, 用以解决提出的研究问题. 图3中显示了实验研究设计流程. 下面将依次介绍设计流程的每个部分.

图 3 实验设计流程

3.1 实验程序

本文选择了错误定位领域常用的软件基准程序库(Subject Infrastructure Repository, SIR)^[27]中的5个程序作为实验对象, 分别为printtokens2, schedule2, totinfo, tcas和sed. 这些程序均为开源的C程序, 其中前4个程序来自西门子套件(Siemens Suite), sed是大型的真实错误程序. 实验中使用的错误版本和测试用例均可在SIR库中下载. 这些程序在高阶变异测试领域中广泛使用^[12,28-30], 同时也经常应用在错误定位等相关的研究中^{[18,19,23,26]}. 因此我们认为本文测试数据集所得出的结论具有一定的普适性.

表2列出了基准程序的具体信息, 包括程序名称, 程序所有的版本数量和实验中使用的数量, 程序的平均代码行以及FOMs和HOMs的数量. 其中, FOMs列的“生成的数量”子列表示对应程序生成的FOMs总数, 而“使用”子列表示实验中实际运行的FOMs总数. 本文共选择了63个单错误版本程序作为实验对象, 部分版本因为错误语句无法生成有效变异体而导致测试用例无法检测出该版本的错误, 或因为执行过程中出现异常, 无法收集到完整的执行信息.

表 2 实验基准程序及变异体信息

3.2 生成变异体

为了研究FOMs和HOMs在单错误和多错误程序中的表现, 实验首先需要生成FOMs和HOMs. 在这个步骤中, 我们收集被失败测试用例覆盖的程序语句, 通过变异算子植入错误到这些语句, 进而生成相应的变异体. 表3列出了Agrawal等^[16]提出的10种经典C语言变异算子.

表 3 经典C语言变异算子

对于生成FOMs, 我们对fail测试用例覆盖的每条语句使用所有变异算子进行变异, 每次只对一条语句变异, 最终生成161218个FOMs. 表2“FOMs”列的“(使用)”子列中列出了每个程序所使用的FOMs数量.

对于生成高阶变异体, 在已有高阶变异测试的研究中, 对变异体阶数的研究有所不同, 有关注于阶数较低(2至4阶)的研究^{[15,28,29,31]}, 也有关注阶数较高(2至15阶)的研究^[12,32-35]. 本文首次考虑将高阶变异体应用于多错误定位, 然而在实际程序中错误数量是不可知的, 因此结合前人的研究成果, 我们选择生成2至7阶的变异体来模拟多错误情况. 在此基础上, 为了进一步探究不同变异位置的高阶变异体与错误定位的关系, 我们依据不同的变异位置对变异体进行了划分, 并通过理论和实验分析发现错误语句处生成的变异体(如准确HOMs和部分准确HOMs)具有更优的错误定位效果. 另一方面, 考虑到MBFL巨大的执行开销, 我们选择生成每阶HOMs的数量与FOMs数量相同来减少HOMs的数量. 假设生成1000个FOMs, 然后2阶变异体和3阶变异体的数量也是1000; 因此最终生成的HOMs为6000. 在我们的实验中, 采用一阶变异算子FOP构建HOMs. 具体来说, 首先随机选择k条失败测试用例覆盖的语句, 然后对每条选择的语句, 随机选择一个与其相对应的一阶变异算子, 最终生成一个k阶变异体. 实验共生成967308个HOMs, 其中实际使用的数量如表2所示(“HOMs”列的“(使用)”子列).

3.3 构建多错误定位场景

为了构建实验中的多错误定位场景, 我们通过随机组合SIR库中的原始单错误程序获得多错误程序. 每个多错误程序中的错误数量是2到5个. 最终生成100个版本的多错误程序. 最后, 依据多错误程序生成的变异体, 运行变异体收集测试结果用于效果分析.

3.4 评估MBFL的效果

为了评估FOMs和HOMs在MBFL中的定位效果, 我们使用了3种研究人员常用的评估指标^[36-39].

(1) EXAM: EXAM^[36,37]是错误定位领域广泛使用的评价指标之一, 用于评估开发人员找到准确错误位置之前需要检查的程序实体的比例, 因此EXAM值越小表明对应的错误定位效果越好^[36,37]. EXAM的公式定义如下:

$ EXAM = \frac{{rank}}{{{\rm{Number\; of\; executable\; statement}}}} $

(6)

式(6)中, 分子是错误语句的排名, 分母是需要检查的程序语句数量的总和.rank的计算公式为:

$ rank = \frac{{(i + 1) + (i + j)}}{2} $

(7)

式(7)中, i表示怀疑度值大于错误语句的正确语句的数量, j表示怀疑度值等于错误语句的正确语句的数量. 为更接近真实定位场景, 我们选择第i+1位排名与第i+j位排名的平均作为错误语句的排名.

(2) Top-N: Top-N用于评估排名前N个程序候选元素中, 能定位到真实错误的个数^[38]. 在Kochhar等的研究发现, 73.58%的开发者只检查排名前5的程序元素, 并且几乎所有的开发者认为检查排名前10的程序元素是可接受的上限^[39]. 因此, 参考之前的研究^[36,38], 我们将N设定为1, 3, 5. 同时, 假设两条语句有相同的怀疑度, 我们同样计算这些语句排名的平均值(如式(7)所示). Top-N越大表明对应的错误定位技术越好.

(3) MAP: MAP (Mean Average Precision)是信息检索领域用于评估语句排序质量的指标, 是所有错误平均精度的平均值^[40]. AP(Average Precision)的计算公式如下:

$ AP = \sum\limits_{i = 1}^M {\frac{{P(i) \times pos(i)}}{{{\rm{number\; of\; faulty \;statements}}}}} $

(8)

式(8)中, i是程序语句的排名, M是排名列表中语句的总数, pos(i)是布尔函数, pos(i)=1表示第i条语句是错误的, 反之pos(i)=0表示第i条语句是正确的. P(i)是每个排名i的定位精度.

$ P(i) = \frac{{{\rm{number\; of\; faulty\; statements\; in\; top \;}}i\;{\rm{ ranks}}}}{i} $

(9)

MAP是错误集合的AP的平均值, MAP越大表明对应的错误定位技术越好.

4 实验结果 4.1 研究问题

为了评估HOMs是否能提高错误定位的精度, 本文从错误定位精度角度出发, 提出如下研究问题:

(1) RQ1: 与FOMs相比, 不同阶数的HOMs的多错误定位精度如何？

(2) RQ2: 与FOMs相比, 不同类型的HOMs的多错误定位精度如何？

4.2 实验结果

为探究RQ1, 我们首先针对多错误程序生成一阶HOMs, 然后运行这些变异体计算得到每个程序对应的EXAM, Top-N和MAP. 本文使用Metallaxis-FL 为原始MBFL对照组, 并生成2阶到7阶的HOMs.

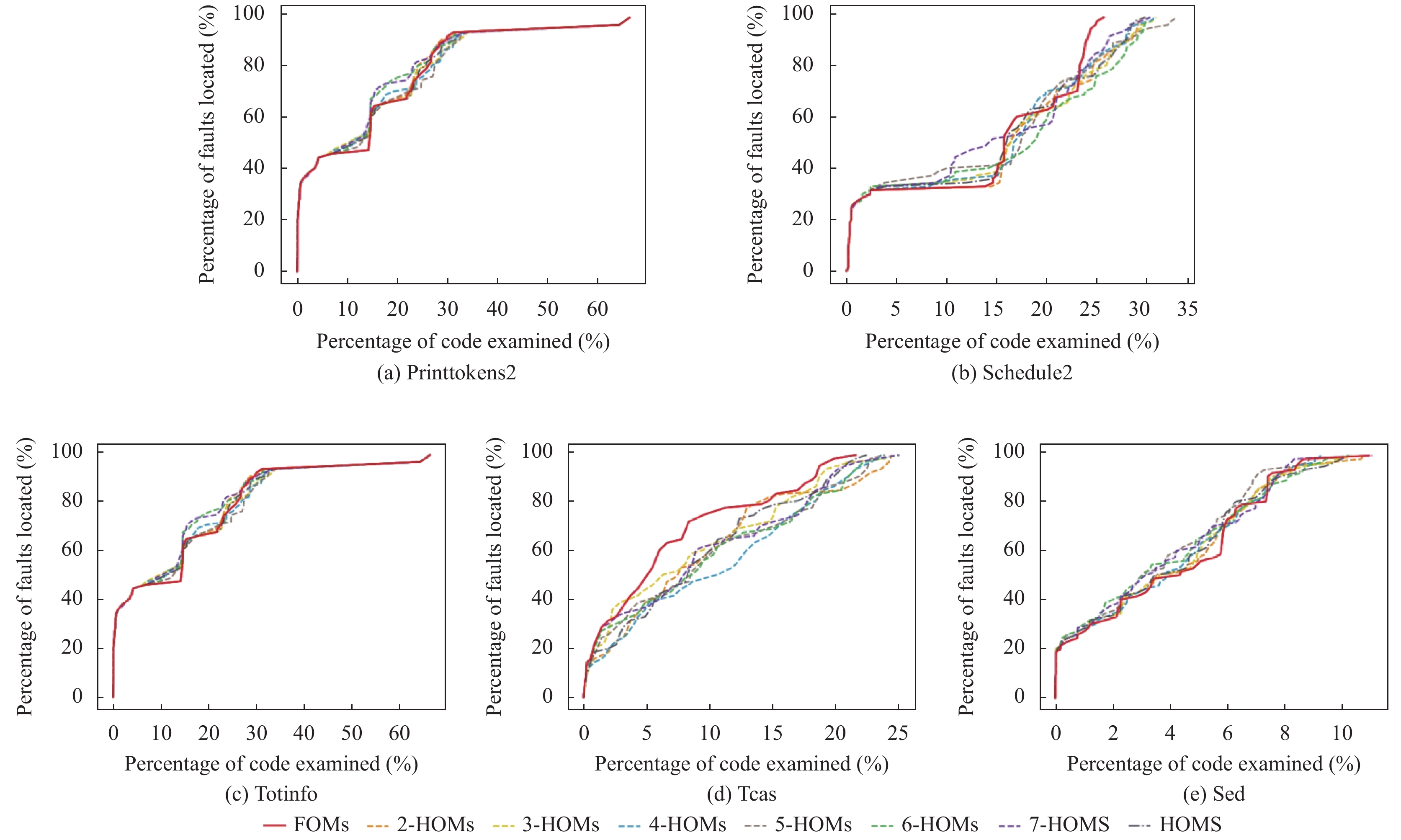
图4中展示了MBFL使用FOMs和不同阶的HOMs的错误检查比例. x轴表示代码检查比例, y轴表示不同程序所有错误版本查找到的累积错误比例, 对应的曲线越接近y轴表明对应的变异体的检测错误数量越多, 因此对应的变异体错误定位效果更好.

图 4 FOMs 与不同阶 HOMs 的代码检查比例比较

从图4(a)中可以看出, 7-HOMs检测20%的程序代码能检测到68%的错误, 而FOMs只能检测到55%的错误. 同理, 在schedule2, totinfo和sed上可以看出, HOMs检测更少的代码能检测到更多的错误, 但在tcas程序上FOMs的检测效果优于HOMs.

从Top-1, Top-3, Top-5指标来看, FOMs在2错误程序上的定位效果比HOMs更好, 而HOMs在3错误和5错误程序上的表现比FOMs更好. 表4中显示了FOMs和HOMs在多错误程序定位场景下排在前1, 3, 5位错误的数量. 图中包括4种错误数量的程序统计结果. 对2错误程序, FOMs和各阶高阶变异体都将19个错误排在第一名. 除了7-HOMs, FOMs比其他阶数的HOMs的Top-3, Top-5要更高. 对3错误程序, 3-HOMs比FOMs和其他阶数的变异体在Top-3和Top-5上更高. 同时FOMs在4错误程序中, Top-3和Top-5上的表现略优于HOMs. 最后, 在5错误程序上, FOMs、6-HOMs和7-HOMs的Top-1值最高, 而6-HOMs和3-HOMs分别在Top-3和Top-5上表现最好.

从MAP指标来看, FOMs在4错误程序上表现最优, 在其他错误程序上与HOMs有相近的表现. 从表5可以看出, FOMs在4错误程序上的MAP均值最高. 在其他错误程序上与HOMs有相近的表现, 例如3错误程序FOMs的MAP均值与4阶到7阶的变异体的MAP均值相同.

综上可以看出, HOMs在一些程序上的检错能力优于FOMs. 同时, FOMs在2错误和4错误程序上的定位效果较好, 而HOMs在3错误和5错误程序上的效果更好. HOMs在3错误和4错误程序上有更大的Top-N值, 并且在一些阶数的HOMs下, 计算的MAP均值都要高于FOMs.

表 4 FOMs和不同阶HOMs的TOP-N值比较

指标	程序		FOMs			2-HOMs				3-HOMs				4-HOMs				5-HOMs				6-HOMs				7-HOMs				HOMs
指标	程序	Top	1	3	5		1	3	5		1	3	5		1	3	5		1	3	5		1	3	5		1	3	5		1	3	5
2错误	printtokens2		6	8	8	6		8	8	6		8	8	6		8	8	6		8	8	6		8	8	6		8	8	6		8	8
	schedule2		4	6	6	4		6	6	4		6	6	4		6	6	4		6	6	4		6	6	4		6	6	4		6	6
	totinfo		3	5	6	3		5	6	3		5	6	3		5	6	3		5	6	3		5	6	3		5	6	3		5	6
	tcas		2	6	7	2		4	5	2		5	6	2		5	6	2		5	6	2		5	6	2		6	6	2		3	4
	sed		4	5	5	4		5	5	4		5	5	4		5	5	4		5	5	4		5	5	4		5	5	4		5	5
	Total		19	30	32	19		28	30	19		29	31	19		29	31	19		29	31	19		29	31	19		30	31	19		27	29
3错误	printtokens2		5	8	9	5		8	9	5		8	9	5		8	9	5		8	9	6		8	8	6		8	8	5		8	9
	schedule2		3	4	4	3		4	4	2		4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4
	totinfo		4	5	6	4		5	6	4		5	6	4		5	6	4		5	6	4		5	6	4		5	6	4		5	6
	tcas		5	5	5	4		5	5	5		5	6	5		5	6	5		5	5	5		5	5	5		5	6	4		5	6
	sed		3	1	1	3		2	2	2		2	2	3		1	1	3		1	1	3		1	1	3		1	1	3		1	2
	Total		20	23	25	19		24	26	18		24	27	20		23	26	20		23	25	20		23	25	20		23	26	19		23	27
4错误	printtokens2		3	4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4
	schedule2		3	4	5	3		4	5	3		4	5	3		4	5	3		4	4	3		4	5	3		4	5	3		4	5
	totinfo		2	3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5
	tcas		1	6	6	1		1	2	2		4	6	1		2	2	1		3	4	1		4	4	1		5	5	2		3	5
	sed		3	4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4	3		4	4
	Total		12	21	24	12		16	20	13		19	24	12		17	20	12		18	22	12		19	22	12		20	23	13		18	23
5错误	printtokens2		2	3	3	2		3	3	2		3	3	2		3	3	2		3	3	2		3	3	2		3	3	2		3	3
	schedule2		3	4	5	3		4	5	3		4	5	3		4	5	3		4	4	3		4	5	3		4	5	3		4	5
	totinfo		2	3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5	2		3	5
	tcas		3	4	5	2		2	4	0		2	9	0		0	2	1		4	5	3		5	6	3		4	7	2		2	3
	sed		3	3	3	3		3	3	3		3	3	3		3	3	3		3	3	3		3	3	3		3	3	3		3	3
	Total		13	17	21	12		15	20	10		15	25	10		13	18	11		17	21	13		18	23	13		17	23	12		15	19

表 4 FOMs和不同阶HOMs的TOP-N值比较

表 5 FOMs和不同阶HOMs的平均MAP值比较

类型	程序	FOMs	2-HOMs	3-HOMs	4-HOMs	5-HOMs	6-HOMs	7-HOMs	HOMs
2错误	printtokens2	0.0022	0.0022	0.0022	0.0022	0.0022	0.0022	0.0022	0.0022
	schedule2	0.0024	0.0024	0.0024	0.0024	0.0024	0.0024	0.0024	0.0024
	totinfo	0.0018	0.0018	0.0018	0.0018	0.0018	0.0018	0.0018	0.0018
	tcas	0.0042	0.0031	0.0033	0.0038	0.0036	0.0038	0.0039	0.0041
	sed	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
	Average	0.0021	0.0019	0.0020	0.0021	0.0020	0.0021	0.0021	0.0021
3错误	printtokens2	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015
	schedule2	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010
	totinfo	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015	0.0015
	tcas	0.0041	0.0032	0.0032	0.0041	0.0041	0.0041	0.0040	0.0040
	sed	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0016	0.0014	0.0014	0.0016	0.0016	0.0016	0.0016	0.0016
4错误	printtokens2	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007
	schedule2	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010	0.0010
	totinfo	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007
	tcas	0.0014	0.0012	0.0010	0.0013	0.0010	0.0011	0.0011	0.0013
	sed	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0008	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007
5错误	printtokens2	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004
	schedule2	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007	0.0007
	totinfo	0.0006	0.0006	0.0006	0.0006	0.0006	0.0006	0.0006	0.0006
	tcas	0.0017	0.0013	0.0014	0.0008	0.0005	0.0011	0.0017	0.0016
	sed	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0007	0.0006	0.0006	0.0005	0.0004	0.0006	0.0007	0.0007

表 5 FOMs和不同阶HOMs的平均MAP值比较

由于FOMs只使用一次变异算子生成而HOMs使用多次变异算子生成. 因此在对同一个程序变异生成等量变异体时, HOMs有更大的概率变异到错误语句, 从而增大变异体被杀死的概率, 相应a_kf值也会更高, 则变异体怀疑度也越高, 最终计算的语句怀疑度也越高, 其定位效果也更优(如图4(a), 图4(c), 图4(e); 表4“3错误”行, “5错误”行; 表5 “3错误”行, “5错误”行). 但如果HOMs中更多变异体是对正确语句变异生成的, 那么相应的a_kp值会更高, 计算的语句怀疑度值也更高, 错误定位效果将更差. (如图4(d); 表4 “2错误”行, “4错误”行; 表5 “2错误”行, “4错误”行). 综合比较可以得出HOMs在一定程度上能提高多错误定位的效果.

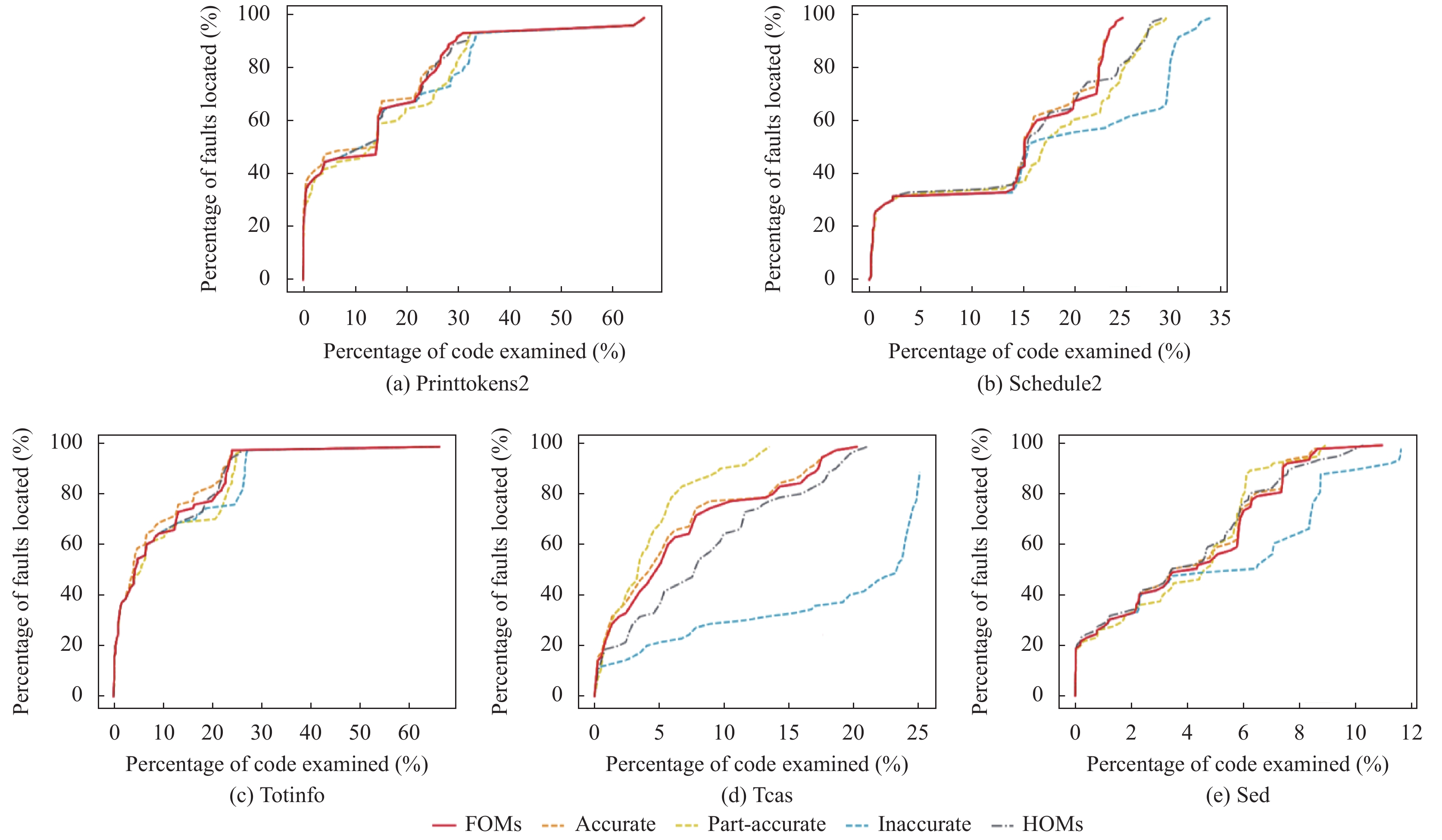
为探究RQ2, 我们首先收集多错误程序所有版本下3类HOMs的EXAM值, 然后分别计算Top-N和MAP指标. 为了便于展示, 我们将3类HOMs分别表示为“Accurate”(准确HOMs), “Part-accurate”(部分准确HOMs)和“Inaccurate”(不准确HOMs). 图5表示MBFL使用FOMs和3类HOMs在不同程序上所有版本的错误检查比例. 从图5(a)–图5(c)中可以看出Accurate HOMs与FOMs有相近的表现, 并且Accurate HOMs的检测效果优于FOMs. 而在tcas和sed (图5(d)、图5(e))程序上, Part-accurate的检测效果更好, 检查更少量的代码而找到更多的错误. 同时在所有程序上, Inaccurate的检测效果最差.

图 5 FOMs 与不同类 HOMs 代码检查比例比较

从Top-N指标来看, 准确HOMs比FOMs和另外两类变异体能将更多错误排在前1, 3, 5名. 表6中显示, 在2错误程序上, 准确变异体与FOMs能够排列相同数量的错误在Top-1, Top-3和Top-5, 而在其他错误程序版本中, 准确HOMs的Top-N指标均为最大. 同时可以发现, 部分准确HOMs在4错误和5错误程序上, 有更高的Top-5值. 然而不准确HOMs 的表现最差.

从MAP指标来看, 准确HOMs的表现同样优于FOMs, 部分准确和不准确HOMs. 表7中准确HOMs与FOMs在2错误程序下有相同MAP平均值, 而在3, 4, 5错误程序下, 准确HOMs仍然比另外两类变异体的定位效果好, 其MAP平均值分别为0.0017, 0.0009, 和0.0008.

综上所述我们可以发现, 准确HOMs的错误定位精度高于FOMs、部分准确HOMs和不准确HOMs. 在一些情况下, 部分准确HOMs有更好的定位效果, 但普遍情况下不准确HOMs的表现都很差.

表 6 FOMs和不同类HOMs的Top-N值比较

类型	程序		FOMs			Accurate				Part-accurate				Inaccurate				HOMs
类型	程序	Top	1	3	5		1	3	5		1	3	5		1	3	5		1	3	5
2错误	printtokens2		6	8	8		6	8	8		6	7	7		6	8	8		6	8	8
	schedule2		4	6	6		4	6	6		4	6	6		4	6	6		4	6	6
	totinfo		3	5	6		3	5	6		3	5	6		3	5	6		3	5	6
	tcas		2	6	7		2	6	7		2	6	6		2	2	4		2	3	4
	sed		4	5	5		4	5	5		4	4	5		4	5	5		4	5	5
	Total		19	30	32		19	30	32		19	28	30		19	26	29		19	27	29
3错误	printtokens2		5	8	9		6	9	10		5	6	6		5	8	9		5	8	9
	schedule2		3	4	4		3	4	4		3	4	4		3	4	4		3	4	4
	totinfo		4	5	6		4	5	6		4	5	6		4	5	6		4	5	6
	tcas		5	5	5		5	5	5		4	5	6		5	5	5		4	5	6
	sed		3	1	1		3	1	1		3	1	1		3	1	1		3	1	2
	Total		20	23	25		21	24	26		19	21	23		20	23	25		19	23	27
4错误	printtokens2		3	4	4		5	5	5		3	4	4		3	4	4		3	4	4
	schedule2		3	4	5		3	4	5		3	4	5		3	4	5		3	4	5
	totinfo		2	3	5		2	3	5		2	3	5		2	3	5		2	3	5
	tcas		1	6	6		1	7	7		2	6	8		1	1	1		2	3	5
	sed		3	4	4		3	4	4		3	4	4		3	4	4		3	4	4
	Total		12	21	24		14	23	26		13	21	26		12	16	19		13	18	23
5错误	printtokens2		2	3	3		2	3	3		2	3	3		2	3	3		2	3	3
	schedule2		3	4	5		2	4	5		3	4	5		3	4	5		3	4	5
	totinfo		2	3	5		2	3	5		2	3	5		2	3	5		2	3	5
	tcas		3	4	5		4	5	7		0	6	10		0	0	0		2	2	3
	sed		3	3	3		3	3	3		2	3	3		3	3	3		3	3	3
	Total		13	17	21		14	18	23		8	19	26		10	13	16		12	15	19

表 6 FOMs和不同类HOMs的Top-N值比较

表 7 FOMs和不同类HOMs的MAP值比较

类型	程序	FOMs	Accurate	Part-accurate	Inaccurate	HOMs
2错误	printtokens2	0.0022	0.0022	0.0020	0.0022	0.0022
	schedule2	0.0024	0.0024	0.0024	0.0024	0.0024
	totinfo	0.0018	0.0018	0.0018	0.0018	0.0018
	tcas	0.0042	0.0042	0.0040	0.0028	0.0041
	sed	0.0001	0.0001	0.0001	0.0001	0.0001
	Average	0.0021	0.0021	0.0021	0.0019	0.0021
3错误	printtokens2	0.0015	0.0018	0.0012	0.0015	0.0015
	schedule2	0.0010	0.0010	0.0010	0.0010	0.0010
	totinfo	0.0015	0.0016	0.0015	0.0015	0.0015
	tcas	0.0041	0.0041	0.0034	0.0039	0.0040
	sed	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0016	0.0017	0.0014	0.0016	0.0016
4错误	printtokens2	0.0007	0.0010	0.0006	0.0007	0.0007
	schedule2	0.0010	0.0010	0.0010	0.0010	0.0010
	totinfo	0.0007	0.0007	0.0007	0.0007	0.0007
	tcas	0.0014	0.0016	0.0017	0.0007	0.0013
	sed	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0008	0.0009	0.0008	0.0006	0.0007
5错误	printtokens2	0.0004	0.0004	0.0004	0.0004	0.0004
	schedule2	0.0007	0.0007	0.0006	0.0007	0.0006
	totinfo	0.0006	0.0006	0.0006	0.0006	0.0006
	tcas	0.0017	0.0022	0.0012	0.0002	0.0016
	sed	0.0000	0.0000	0.0000	0.0000	0.0000
	Average	0.0007	0.0008	0.0006	0.0004	0.0006

表 7 FOMs和不同类HOMs的MAP值比较

三类HOMs由于其不同的生成机制, 造成最终定位效果的差异. 首先, 准确HOMs准确变异错误语句, 并且对正确语句不作任何变异, 几乎能够被所有的失败测试用例杀死而不被通过测试用例杀死, 其a_kf值高且a_kp值低, 因此最终计算的错误语句的怀疑度值会高, 其定位效果也就更优(如图5, 表6, 表7). 其次, 部分准确HOMs同时对错误语句和正确语句变异, 会被部分失败测试用例和正确测试用例杀死. 其定位效果取决于被失败测试用例杀死的比例, 比例较高则定位精度高, 比例较低则定位精度低. 因此部分准确HOMs的定位效果存在波动(如图5, 表6 “5错误”行, 表7). 最后, 不准确HOMs只变异正确语句, 不对错误语句进行变异, 那么其更容易被正确测试用例杀死且不易被失败测试用例杀死, 计算的错误语句的怀疑度较低, 定位效果也就最差(如图5, 表6, 表7). 因此生成一些特定的HOMs, 比如准确HOMs, 能有效提升多错误定位的精度.

5 结论与展望

为探究HOMs是否能提升多错误程序定位, 本文进行了大规模的实证研究. 研究结果发现, HOMs在3错误和5错误程序上, 有更高的错误定位精度. 根据不同的变异位置, 我们将HOMs分成3类. 我们发现准确HOMs比FOMs和其他两类变异体有更好的多错误定位效果. 因此, HOMs在一定程序上能够提升多错误程序定位, 并建议研究人员设计方法生成更有效的变异体, 比如准确HOMs. 在后续的研究中, 作者将研究新的策略用于选择有效提升多错误定位精度的变异体. 同时考虑扩大实验数据集来验证HOMs对错误定位的影响.

参考文献

[1]	Howden WE. Theoretical and empirical studies of program testing. IEEE Transactions on Software Engineering, 1978, SE-4(4): 293-298. DOI:10.1109/TSE.1978.231514
[2]	Zhang XY, He HF, Gupta N, et al. Experimental evaluation of using dynamic slices for fault location. Proceedings of the 6th International Symposium on Automated Analysis-Driven Debugging. Monterey, CA, USA. 2005. 33–42.
[3]	Wong WE, Gao RZ, Li YH, et al. A survey on software fault localization. IEEE Transactions on Software Engineering, 2016, 42(8): 707-740. DOI:10.1109/TSE.2016.2521368
[4]	Arrieta A, Segura S, Markiegi U, et al. Spectrum-based fault localization in software product lines. Information and Software Technology, 2018, 100: 18-31. DOI:10.1016/j.infsof.2018.03.008
[5]	Papadakis M, Le Traon Y. Metallaxis-FL: Mutation-based fault localization. Software: Testing, Verification and Reliability, 2015, 25(5–7): 605-628.
[6]	Keller F, Grunske L, Heiden S, et al. A critical evaluation of spectrum-based fault localization techniques on a large-scale software system. Proceedings of 2017 IEEE International Conference on Software Quality, Reliability and Security (QRS). Prague, Czech Republic. 2017. 114–125.
[7]	Papadakis M, Le Traon Y. Using mutants to locate "unknown" faults. Proceedings of the IEEE 5th International Conference on Software Testing, Verification and Validation. Montreal, QC, Canada. 2012. 691–700.
[8]	Kooli M, Kaddachi F, Di Natale G, et al. Computing reliability: On the differences between software testing and software fault injection techniques. Microprocessors and Microsystems, 2017, 50: 102-112. DOI:10.1016/j.micpro.2017.02.007
[9]	Moon S, Kim Y, Kim M, et al. Ask the mutants: Mutating faulty programs for fault localization. Proceedings of the IEEE 7th International Conference on Software Testing, Verification and Validation. Cleveland, OH, USA. 2014.153–162.
[10]	Papadakis M, Le Traon Y. Effective fault localization via mutation analysis: A selective mutation approach. Proceedings of the 29th Annual ACM Symposium on Applied Computing. Gyeongju, Republic of Korea. 2014. 1293–1300.
[11]	Pearson S, Campos J, Just R, et al. Evaluating and improving fault localization. Proceedings of the IEEE/ACM 39th International Conference on Software Engineering (ICSE). Buenos Aires, Argentina. 2017. 609–620.
[12]	Jia Y, Harman M. Higher order mutation testing. Information and Software Technology, 2009, 51(10): 1379-1393. DOI:10.1016/j.infsof.2009.04.016
[13]	Liu Y, Li Z, Zhao RL, et al. An optimal mutation execution strategy for cost reduction of mutation-based fault localization. Information Sciences, 2018, 422: 572-596. DOI:10.1016/j.ins.2017.09.006
[14]	Xue XZ, Namin AS. How significant is the effect of fault interactions on coverage-based fault localizations? Proceedings of 2013 ACM/IEEE International Symposium on Empirical Software Engineering and Measurement. Baltimore, MD, USA. 2013. 113–122.
[15]	Offutt AJ. Investigations of the software testing coupling effect. ACM Transactions on Software Engineering and Methodology, 1992, 1(1): 5-20. DOI:10.1145/125489.125473
[16]	Agrawal H, DeMillo RA, Hathaway B, et al. Design of mutant operators for the C programming language. West Lafayette, IN, USA: Software Engineering Research Center, Purdue University, 1989, SERC-TR-41-P.
[17]	Abreu R, Zoeteweij P, Van Gemund AJC. An evaluation of similarity coefficients for software fault localization. Proceedings of the 12th Pacific Rim International Symposium on Dependable Computing (PRDC’06). Riverside, CA, USA. 2006. 39–46.
[18]	Jones JA, Harrold MJ, Stasko J. Visualization of test information to assist fault localization. Proceedings of the 24th International Conference on Software Engineering. Orlando, FL, USA. 2002. 467–477.
[19]	Wong WE, Debroy V, Gao RZ, et al. The DStar method for effective software fault localization. IEEE Transactions on Reliability, 2014, 63(1): 290-308. DOI:10.1109/TR.2013.2285319
[20]	Shin D, Bae DH. A theoretical framework for understanding mutation-based testing methods. Proceedings of 2016 IEEE International Conference on Software Testing, Verification and Validation (ICST). Chicago, IL, USA. 2016. 299–308.
[21]	Gopinath R, Jensen C, Groce A. The theory of composite faults. Proceedings of 2017 IEEE International Conference on Software Testing, Verification and Validation (ICST). Tokyo, Japan. 2017. 47–57.
[22]	Langdon WB, Harman M, Jia Y. Efficient multi-objective higher order mutation testing with genetic programming. Journal of Systems and Software, 2010, 83(12): 2416-2430. DOI:10.1016/j.jss.2010.07.027
[23]	Wang HF, Du B, He J, et al. IETCR: An information entropy based test case reduction strategy for mutation-based fault localization. IEEE Access, 2020, 8: 124297-124310. DOI:10.1109/ACCESS.2020.3004145
[24]	Hamill M, Goseva-Popstojanova K. Common trends in software fault and failure data. IEEE Transactions on Software Engineering, 2009, 35(4): 484-496. DOI:10.1109/TSE.2009.3
[25]	DiGiuseppe N, Jones JA. On the influence of multiple faults on coverage-based fault localization. Proceedings of 2011 International Symposium on Software Testing and Analysis. Toronto, ON, Canada. 2011. 210–220.
[26]	Debroy V, Wong WE. Combining mutation and fault localization for automated program debugging. Journal of Systems and Software, 2014, 90: 45-60. DOI:10.1016/j.jss.2013.10.042
[27]	Do H, Elbaum S, Rothermel G. Supporting controlled experimentation with testing techniques: An infrastructure and its potential impact. Empirical Software Engineering, 2005, 10(4): 405-435. DOI:10.1007/s10664-005-3861-2
[28]	Jia Y, Harman M. Constructing subtle faults using higher order mutation testing. Proceedings of the 8th IEEE International Working Conference on Source Code Analysis and Manipulation. Beijing, China. 2008. 249–258.
[29]	Papadakis M, Malevris N. An empirical evaluation of the first and second order mutation testing strategies. Proceedings of the 3rd International Conference on Software Testing, Verification, and Validation Workshops. Paris, France. 2010. 90–99.
[30]	Wu F, Harman M, Jia Y, et al. Homi: Searching higher order mutants for software improvement. Proceedings of the 8th International Symposium on Search Based Software Engineering. Raleigh, NC, USA. 2016. 18–33.
[31]	Langdon WB, Harman M, Jia Y. Multi objective higher order mutation testing with genetic programming. Proceedings of 2009 Testing: Academic and Industrial Conference-Practice and Research Techniques. Windsor, UK. 2009. 21–29.
[32]	Omar E, Ghosh S, Whitley D. Constructing subtle higher order mutants for Java and AspectJ programs. Proceedings of the IEEE 24th International Symposium on Software Reliability Engineering (ISSRE). Pasadena, CA, USA. 2013. 340–349.
[33]	Nguyen QV, Madeyski L. On the relationship between the order of mutation testing and the properties of generated higher order mutants. Proceedings of 8th Asian Conference on Intelligent Information and Database Systems. Da Nang, Vietnam. 2016. 245–254.
[34]	Nguyen QV, Madeyski L. Searching for strongly subsuming higher order mutants by applying multi-objective optimization algorithm. In: Le Thi HA, Nguyen NT, Van Do T, eds. Advanced Computational Methods for Knowledge Engineering. Cham: Springer, 2015. 391–402.
[35]	Nguyen QV, Madeyski L. Empirical evaluation of multiobjective optimization algorithms searching for higher order mutants. Cybernetics and Systems, 2016, 47(1–2): 48-68.
[36]	Li X, Li W, Zhang YQ, et al. DeepFL: Integrating multiple fault diagnosis dimensions for deep fault localization. Proceedings of the 28th ACM SIGSOFT International Symposium on Software Testing and Analysis. Beijing, China. 2019. 169–180.
[37]	Zou DM, Liang JJ, Xiong YF, et al. An empirical study of fault localization families and their combinations. IEEE Transactions on Software Engineering, 2019.
[38]	Le TDB, Lo D, Le Goues C, et al. A learning-to-rank based fault localization approach using likely invariants. Proceedings of the 25th International Symposium on Software Testing and Analysis. Saarbrücken, Germany. 2016. 177–188.
[39]	Kochhar PS, Xia X, Lo D, et al. Practitioners' expectations on automated fault localization. Proceedings of the 25th International Symposium on Software Testing and Analysis. 2016: 165-176.
[40]	Moffat A, Zobel J. Rank-biased precision for measurement of retrieval effectiveness. ACM Transactions on Information Systems, 2008, 27(1): 2.