2. 中国民航大学 航空工程学院, 天津300300;
3. 天津迅联科技有限公司, 天津 300300
2. School of Aeronautical Engineering, Civil Aviation University of China, Tianjin 300300, China;
3. Tianjin Xunlian Technology Co. Ltd., Tianjin 300300, China
近年来, 无人机产业在中国快速发展, 适用于无人机的场景持续扩大, 无人机飞行控制技术也不断发展, 逐步成为航空领域第一线的热点. 随着微型控制器、信息技术、航空强化推进技术等的成熟, 大大降低了生产成本, 人工智能技术与其融合, 促进了高级智能控制算法与飞机操作的有机结合.
四旋翼飞行器是一种通过改变4个转轴的转速来实现对飞行姿态与位置控制的无人飞行器. 4个旋翼均匀分布使得机体受力均匀, 它的结构紧凑相比于单独的旋翼控制飞行姿态更稳定. 突发的肺炎病毒疫情, 导致大部分人在家中隔离, 无人机行业的实用性得到了充分的展现, 能够满足相关方面的需求, 并很大程度上降低了人员之间的病毒传播, 如给隔离小区喷洒消毒、监督行人口罩佩戴、配送物资等. 通过四旋翼飞行器控制算法与先进智能控制相结合, 来克服四旋翼飞行器在执行工作过程中稳态精度低, 抗干扰能力差、响应速度慢和鲁棒性差等问题.
目前应用在无人机上的主流控制算法有传统PID控制[1]、线性二次型调节控制[2]、反步法控制[3]、模糊自适应控制[4]、神经网络控制[5]等. 中国计量学院的李俊等[6]通过对四轴飞行器动力学建立, 并对设计的PID控制有效性验证; 沈阳航空航天大学的李一波等[7]在将传统PID与模糊控制技术相结合设计了双环控制器应用到四旋翼无人机中; 清华大学的李卓等[8]提出BP神经网络模糊自适应PID控制器, 该控制器具有较强的适应能力和较好的鲁棒性优点; 北京航空航天大学的蒋景旺等[9]将神经网络模糊PID控制应用在高低温环境模拟系统中对温度控制范围与控制精度均有较好的控制效果.
控制算法的性能决定无人机飞行中控制效果, 传统的PID控制算法具有简单易实现的优点, 但是对控制器的最优控制参数的设定较为困难, 四旋翼飞行器工作环境经常发生变化, 原有的控制参数达不到最佳控制效果. 模糊PID控制器能够利用模糊规则表对不同时刻的飞行误差和误差变化率进行微调, 但对于通过直觉和经验获取的复杂专家知识不易用规则表示, 对模糊规则的制定与隶属度函数的选择不够精确, 通过微调后控制效果可能不如传统PID. 神经网路结合传统的控制算法已经在很多领域得到了应用, 利用神经网络的自学习能力, 对模糊控制算法的输入输出样本进行学习, 生成更加精确的模糊规则, 提升控制算法控制效果. 将设计的神经模糊PID控制器应用到四旋翼飞行器中: 1)能提高系统是快速响应和抗干扰能力; 2)使得控制算法即有神经网络的自学习能力又有模糊控制的知识表达能力.
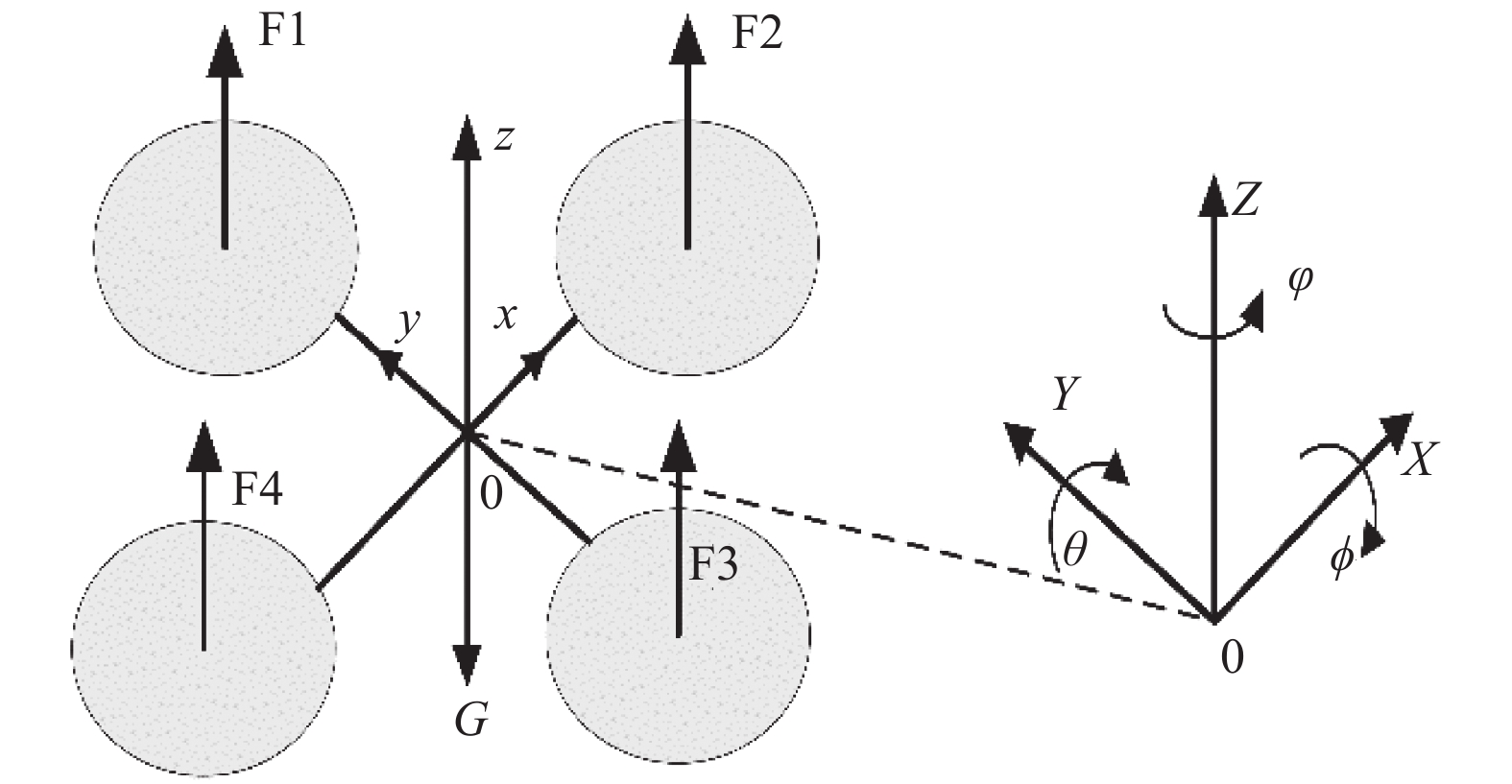
1 动力学模型的建立在建立惯性坐标系(OXYZ)和机体坐标系B(oxyz)基本坐标系的基础上[10], 来计算四旋翼飞行器的数学模型, 见图1.
对欧拉角进行如下定义: 俯仰角
|
图 1 惯性坐标系和机体坐标系 |
为了建立四旋翼飞行器的动力学模型[6], 综合考虑对四旋翼飞行器做出如下假设:
① 四旋翼飞行器是对称且运动和受力不发生改变的物体;
② 重力加速度不会受到飞行高度影响而发生改变;
③ 空气阻力对四旋翼飞行器不产生影响;
在建立上述坐标系的基础上, 并且低速没有风飞行的情况下, 忽略阻力系数, 可以得到以下数学模型, 即式中: U1为垂直控制分量、U2为横滚控制分量、U3为俯仰控制分量、U4为偏航控制分量; Ix、Iy、Iz分别为电机在各轴方向上产生的转动惯量.
| $\ddot x = \left( {\cos \varphi \sin \theta \cos \phi + \sin \varphi \sin \phi } \right)U1/m$ | (1) |
| $\ddot y = \left( {\sin \varphi \sin \theta \cos \phi - \sin \phi \cos \varphi } \right)U1/m$ | (2) |
| $\ddot {\textit{z}} = \left( {\cos \theta \cos \phi } \right)U1/m$ | (3) |
| $\ddot \phi = \left[ {lU2 + \dot \theta \dot \varphi \left( {{I_y} - {I_{\textit{z}}}} \right)} \right]/{I_x}$ | (4) |
| $\ddot \theta = \left[ {lU3 + \dot \phi \dot \varphi \left( {{I_{\textit{z}}} - {I_x}} \right)} \right]/{I_y}$ | (5) |
| $\ddot \varphi = \left[ {U4 + \dot \phi \dot \varphi \left( {{I_x} - {I_y}} \right)} \right]/{I_{\textit{z}}}$ | (6) |
通过采用准LPV (Liner Parameter Varying)方法[11,12]对四旋翼无人机的动力学模型进行输入控制量[U1 U2 U3 U4]T线性状态空间表达式. 根据系统的传递函数
| 表 1 四旋翼飞行器参数 |
| 表 2 四旋翼飞行器各通道的传递函数 |
2 控制器设计 2.1 传统PID控制器
采用增量式PID控制[12], 其数学表现形式为:
| $\begin{split} u(k) = &u(k - 1) + {K_p}[e(k) - e(k - 1)] \\ & + {K_i}e(k) + {K_d}[e(k) - 2e(k - 1) + e(k - 2)] \\ \end{split} $ | (7) |
式中, Kp为比例系数, Ki为积分系数, Kd为微分系数, u(k)代表控制器的输出量, 也代表无人机的控制量.
2.2 模糊PID控制器在模糊系统中, 如图2所示, 误差e和误差变化率ec作为模糊PID控制器的输入变量, 它们的基本论域均为[−3,3], Kp的基本论域{−0.3, −0.2, −0.1, 0, 0.1, 0.2, 0.3}, Ki的基本论域{−0.03, −0.02, −0.01, 0, 0.1, 0.2, 0.3}, Kd的基本论域{−0.3, −0.2, −0.1, 0, 0.1, 0.2, 0.3}. 俯仰角和横滚角的基本论域为[−20,20], 偏航角的基本论域为[−180,180], 因此偏航角的误差量化因子Ke为3/180, 俯仰角和横滚角的误差量化因子Ke为3/20, 3个姿态角的误差变化率的量化因子Kec均为3/40, 比例因子KU均取为1, 即实际输出的论域与模糊输出论域一致[13,14]. 由于四旋翼飞行器在执行飞行指令时实时性高, 要求对数据的处理能力较快, 采用较为简单的三角形函数, 可提高推导和计算速度. 模糊控制器有2个输入3个输出, {NB, NM, NS, ZO, PS, PM, PB}即{负大, 负中, 负小, 零, 正小, 正中, 正大}代表它们的模糊变量. 通过研究误差e、误差变化率ec与PID三个参数的变化量之间关系反复实验, 并与国内外专家经验相结合[4,7,15-17], 来制定模糊规则表, 如表3所示.

|
图 2 模糊PID控制器 |
2.3 神经模糊PID控制器 2.3.1 控制器结构
神经模糊PID模型有5层结构[18-20], 它们分别为输入层、隶属度函数生成层、推理层、归一化层以及反模糊化层. 如图3所示, 其中, 第3层的推理层结点个数共有49个, 它们表示模糊规则库生成的49条模糊规则, 并且参数的数值可以通过对模糊语言变量的模糊分割数进行修改.
| 表 3 模糊规则表 |

|
图 3 神经模糊PID结构图 |
第1层是输入层, 它将误差e和误差变化率ec作为输入层的两个输入分量, 用输入向量
第2层将每个
| $A_i^j\left( {{x_i}} \right) = \frac{{{x_i} - {a_{ij}}}}{{b - a}};\;\;i = 1,2,\;j = 1,2, \cdots ,7;$ | (8) |
第3层的将第2层的模糊分割成的语言变量进行匹配, 并计算出不同规则的适用度. 不同的神经元节点表示模糊规则中的不同模糊规则. 即:
| $\left\{\begin{split} & {\alpha _l} = \min \left\{ {A_1^{{i_1}}\left( {{x_1}} \right),A_2^{{i_2}}\left( {{x_2}} \right)} \right\}; \\ & {i_1} \in \left\{ {1,2, \cdots ,7} \right\};{i_2} \in \left\{ {1,2, \cdots ,7} \right\};l = 49; \\ \end{split}\right. $ | (9) |
第4层的神经元节点数与第3层相同, 即m=49, 实现归一化计算, 即:
| ${\hat \alpha _l} = \frac{{{\alpha _l}}}{{\displaystyle\sum\limits_{i = 1}^m {{\alpha _i}} }};l = 1,2, \cdots ,m$ | (10) |
第5层的作用是实现反模糊计算, 即:
| $y = \sum {{\omega _l}} {\hat \alpha _l}$ | (11) |
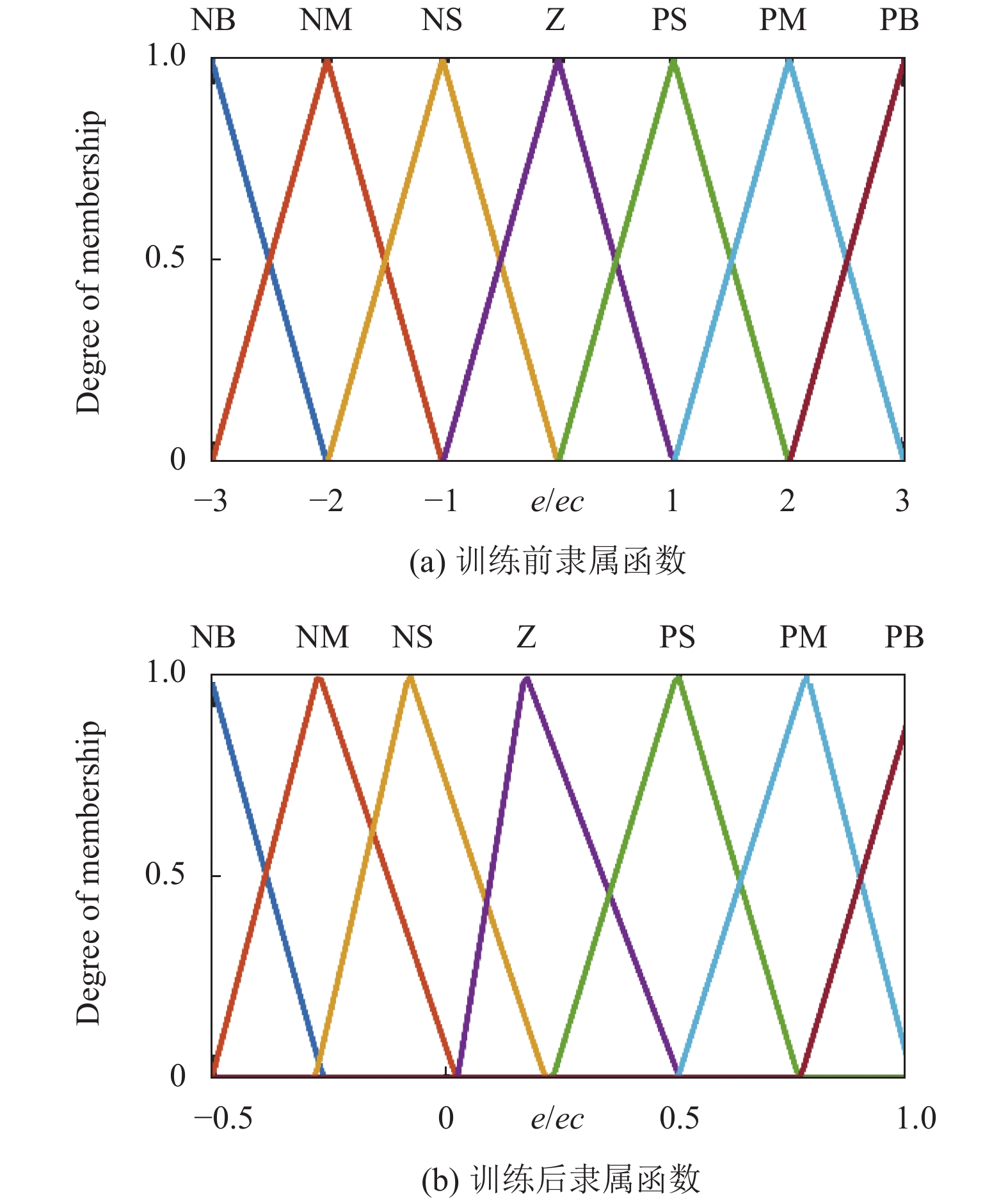
利用传统PID与模糊逻辑相结合的模糊PID控制器应用到四旋翼飞行器中所产生的输入与输出得到神经模糊PID的训练数据. 将数据的70%作为训练集, 数据的30%作为测试集. 采用最小二乘法和反向传播法混合算法(hybrid)训练数据, 设定训练步数echo为500, 训练误差设定为0.01. 由于自适应神经模糊控制器仅支持多输入单输出, 故将P、I、D分别单独训练. 由神经模糊控制系统训练数据的训练集和测试集误差分别为0.0072759和0.00043984, 说明神经网络的性能比较好. 神经网络训练前后模糊逻辑隶属函数的误差及误差变化率的论域进行合理的调整, 如图4所示.
|
图 4 训练前后e、ec对比图 |
3 控制系统的仿真验证
在Matlab/Simulink环境下进行四旋翼飞行器控制系统仿真, 通过对比3种不同控制算法对四旋翼飞行器4个通道的控制效果. 将四旋翼飞行器定高悬停10 s, 位置的初始值是(0,0,0), 期望的目标参数是(0,0,1). 当悬停5 s时给飞行器加入0.5的step函数作为干扰, 观察垂直通道仿真响应情况. 同理, 对姿态角通道进行仿真验证.
由图5仿真结果可得, 传统PID控制达到期望位置响应时间较长, 模糊PID控制在添加干扰后存在一定超调, 调整时间较长. 由表4可以看出, 在垂直通道控制中, 神经模糊PID控制器的四旋翼飞行器上升时间及调整时间明显优于对比算法, 系统稳定后的精度高, 但是初次达到预期位置时还存在一定的超调. 由此可得, 神经模糊PID控制算法在无人机飞行中的具有良好的控制效果.

|
图 5 3种控制器仿真对比 |
| 表 4 垂直通道性能参数表 |
4 结论与展望
本文采用方向余弦法建立了四旋翼飞行器的动力学模型, 将专家经验与多次实验相结合, 制定初步的模糊规则, 利用模糊PID控制得到输入输出数据集. 通过采用最小二乘法和反向传播法混合算法训练数据集来调整模糊规则和隶属度函数得到神经模糊PID控制器.
在Matlab/Simulink环境下仿真, 分别采用传统PID控制器、模糊PID控制器和神经模糊PID控制器3种控制算法对无人机进行控制. 实验结果表明, 设计的神经模糊PID控制器在响应速度, 抗干扰能力及稳态精度均优于对比算法, 但是在垂直通道还一定的微小超调. 在今后的工作中, 我们将结合优秀的智能算法进行改进神经模糊PID控制算法来降低超调量.
| [1] |
余后明. 四旋翼无人机姿态控制研究[硕士学位论文]. 太原: 中北大学, 2019.
|
| [2] |
曾小勇, 彭辉, 吴军. 四旋翼飞行器的建模与姿态控制. 中南大学学报(自然科版), 2013, 44(9): 3693-3700. |
| [3] |
苏丙末, 曹云峰, 陈欣, 等. 基于BACKSTEPPING的无人机飞控系统设计研究. 南京航空航天大学学报, 2001, 33(3): 250-253. DOI:10.3969/j.issn.1005-2615.2001.03.010 |
| [4] |
何乃晨. 基于模糊自适应PID控制的四旋翼无人机飞控系统研究[硕士学位论文]. 天津: 河北工业大学, 2017.
|
| [5] |
余润芝, 赵文龙, 程若发. 四旋翼飞行器的神经网络PID控制算法研究. 现代电子技术, 2019, 42(10): 108-112. |
| [6] |
李俊, 李运堂. 四旋翼飞行器的动力学建模及PID控制. 辽宁工程技术大学学报(自然科学版), 2012, 31(1): 114-117. DOI:10.3969/j.issn.1008-0562.2012.01.028 |
| [7] |
李一波, 宋述锡. 基于模糊自整定PID四旋翼无人机悬停控制. 控制工程, 2013, 20(5): 910-914. DOI:10.3969/j.issn.1671-7848.2013.05.028 |
| [8] |
李卓, 萧德云, 何世忠. 基于神经网络的模糊自适应PID控制方法. 控制与决策, 1996, 11(3): 340-345. DOI:10.3321/j.issn:1001-0920.1996.03.004 |
| [9] |
蒋景旺, 吴云洁, 吴梦晨. 神经网络模糊PID控制在高低温环境模拟系统的应用. 系统仿真学报, 2015, 27(8): 1922-1926. |
| [10] |
Titterton DH, Weston JL. 捷联惯性导航技术. 张天光, 王秀萍, 王丽霞, 等译. 2版. 北京: 国防工业出版社, 2007.
|
| [11] |
江杰, 冯旭光, 苏建彬. 四旋翼无人机仿真控制系统设计. 电光与控制, 2015, 22(2): 27-30. DOI:10.3969/j.issn.1671-637X.2015.02.006 |
| [12] |
刘焕晔. 小型四旋翼飞行器飞行控制系统研究与设计[硕士学位论文]. 上海: 上海交通大学, 2009.
|
| [13] |
宫娟. 基于模糊自适应PID的四旋翼飞行器姿态控制研究[硕士学位论文]. 重庆: 重庆邮电大学, 2018.
|
| [14] |
于文妍, 杨坤林. 四旋翼无人机串级模糊自适应PID控制系统设计. 机械设计与制造, 2019(1): 227-231. DOI:10.3969/j.issn.1001-3997.2019.01.059 |
| [15] |
付岩果. 四旋翼无人机模糊PID姿态控制研究[硕士学位论文]. 舟山: 浙江海洋大学, 2019.
|
| [16] |
Kuantama E, Vesselényi T, Dzitac S, et al. PID and Fuzzy-PID control model for quadcopter attitude with disturbance parameter. International Journal of Computers Communications & Control, 2017, 12(4): 519-532. |
| [17] |
Sio KC, Lee CK. Stability of fuzzy PID controllers. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 1998, 28(4): 490-495. DOI:10.1109/3468.686710 |
| [18] |
刘金琨. 先进PID控制MATLAB仿真. 2版. 北京: 电子工业出版社, 2004.
|
| [19] |
Rezazadeh S, Ardestani MA, Sadeghi PS. Optimal attitude control of a quadrotor UAV using Adaptive Neuro-Fuzzy Inference System (ANFIS). Proceedings of the 3rd International Conference on Control, Instrumentation, and Automation. Tehran, Iran. 2013. 219–223.
|
| [20] |
杨天, 霍琳琳. 一种柔性直流输电系统PID-ANFIS优化控制方法. 电力系统保护与控制, 2015, 43(17): 29-37. DOI:10.7667/j.issn.1674-3415.2015.17.005 |
| [21] |
Jang JSR. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 1993, 23(3): 665-685. DOI:10.1109/21.256541 |
| [22] |
Wang WJ, Huang XT, Huang WT. Design and simulation of heat substation controller based on neural network-fuzzy PID control. Proceedings of 2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics. Hangzhou, China. 2011. 3–6.
|
 2021, Vol. 30
2021, Vol. 30



