这是一个信息爆炸的时代, 大数据这把双刃剑在为我们带来丰富的知识讯息的同时, 也产生了不少“数据泡沫”, 用户常常被这些无效信息包围, 无从下手, 而用户真正感兴趣的信息被阻绝在外. 为了解决这一问题, 推荐系统应运而生, 旨在为每个特定用户从海量数据中筛选出其各自感兴趣的内容并推荐给用户. 推荐系统的关键之一在于对用户兴趣以及物品特征的建模表示, 从而能够进一步通过评分模型对用户、物品预测相关程度, 并以此为依据进行推荐. 另一方面, 社交网络中好友、大V等社交关系也可能会影响用户的潜在兴趣, 社交网络也越来越多地被结合到推荐系统中来^[1-3], 在推荐时利用通过社交网络的传播的信息, 提高了推荐的针对性与有效性.

基于图神经网络(GNNs)的推荐算法^[4,5]是推荐系统应用的热门算法之一. GNN在图结构拓扑上应用深度神经网络的技术对局部图的邻域信息进行迭代, 使得信息能够在非结构化的节点关系中进行交互计算, 最终得到各个节点在图拓扑结构下的特征域表示. 社交推荐本质上是在非规则的用户-物品关系、用户-用户关系中聚合并表示各个节点的本征信息与交互关系, 因此GNN在社交推荐中得到了广泛的应用^[6,7].

图神经网络通常描述的是静态拓扑关系, 一方面, 节点之间的连接关系不会随时间发生改变. 对于推荐系统而言, 时时刻刻都有海量新数据产生, 新用户、新物品以及新交互事件都会改变已有图网络的拓扑结构. 另一方面, 对于特定节点, 其邻居节点的时序性通常被GNN所忽略. 例如, 对于推荐系统中的用户-物品图结构而言, 以用户为中心, 则其邻居节点即为该用户交互过的物品, 而用户与不同物品的交互自然存在时间上的先后, 而交互时间的时序性则可能暗含了用户兴趣随时间的变化情况.

本文主要针对第二点提出改进GNN算法, 利用门控循环单元(GRU)对时间序列信息进行选择性遗忘与选择性记忆, 以此对用户-物品交互历史以及物品-用户交互历史进行建模, 增强了GNN算法在局部图邻域迭代过程中对时序信息的抽象能力, 使得推荐系统对用户节点以及物品节点的表示结合了其特点随时间的变化, 提升了推荐的效果. 具体而言, 我们分别建立了以用户节点为中心的用户-物品图, 每个用户节点的相邻节点为其交互过的物品, 这些相邻节点通过交互时间戳属性排序, 在GNN进行局部图邻域迭代时通过GRU学习物品交互历史潜在关联, 并通过注意力机制与用户表征进行聚合; 类似的, 同时建立以物品节点为中心的物品-用户图, 每个物品节点的相邻节点为与其交互过的用户, 同样按照交互事件的时间戳排序, 并通过注意力GRU模型进行聚合, 以此来表征对该物品感兴趣的群体特征变化; 另外, 还根据用户间的社交关系建立了用户-用户图网络, 通过注意力机制来传递社交网络中相邻用户之间的相互作用.

1 相关工作 1.1 基于非时序特征的GNN推荐算法

深度学习主要关注例如文字的序列结构、例如图片的平面结构, 现在处理这些数据的做法也比较成熟, 关注序列任务的NLP领域多用RNN、Transformer、CNN对数据进行Encoder, 而关注平面结构的CV领域更多使用CNN及其各种变体对数据进行Encoder. 在现实世界中更多的数据表示并不是序列或者平面这种简单的排列, 而是表现为更为复杂的图结构.

Kipf和Welling^[8]提出了用于半监督图分类的图卷积网络(GCNs). 模型通过利用节点属性和图结构来学习节点表示, 它由多个图卷积层组成, 每个图卷积层使用当前节点的表示及其相邻节点的表示的组合来更新节点表示. 通过这个过程, 可以捕获节点之间的依赖关系, 然而在原来的公式中, 当更新节点表示时, 所有的邻居被赋予静态权值. Fan等^[9]通过构建用户−物品关系二元图 (用户购买的所有物品)、用户−朋友关系单元图 (用户的社交关系)、物品−用户关系二元图 (物品被用户购买的记录) 这3个无向图用于对物品进行评分预测. Ying等^[10]构建了用户−标签无向二元图, 通过 PinSage 算法 (随机游走和图卷积结合) 成功应用于超大规模的网页内容推荐. Wang等^[11]构建用户—物品图, 不同之处在于 GNN 算法中使用目标节点及其邻居节点的点积进行更新, 并且通过协同过滤的方法进行推荐. 上述文献证明了图网络在推荐上的有效性, 但都没有考虑时序性对用户兴趣以及物品的影响.

1.2 基于时序特征的推荐算法

对于随时间变化的用户兴趣进行建模在推荐系统领域也引起了大量关注, 这些模型大多基于(高斯)矩阵分解^[12]. 例如, Xiong等^[13]通过分解(用户、物品、时间)张量来学习时间表示. Koren^[14]开发了一个类似的模型叫做timeSVD++. Gopalan等进行了类似的建模, 但是使用了泊松分解^[15]. 但是, 这些方法假定用户的兴趣在长期范围内缓慢而平稳地变化, 通常以月或年为序.

为了有效地捕捉用户的短期兴趣, 最近的研究将RNN引入到用户最近的(有序的)行为模型中. 例如, Hidasi等^[16]首先提出了SessionRNN来模拟用户在会话中的兴趣. Wu等^[17]使用两个独立的RNNs根据新的观察结果更新用户和项的表示. Beutel等^[18]构建了一个基于rnnde的推荐器, 可以包含辅助上下文信息. 本文基于这种思路将GRU引入图网络, 并且辅之以注意力机制, 来捕捉用户的时变兴趣和物品的时变特征, 进而提升了推荐系统在时序评分数据集上的有效性.

2 基于AGRU的图网络社交推荐算法

本文以图网络为骨架建立推荐系统, 定义用户集合 $\left\{ {\mathcal{U}{\rm{|}}{u_1},{u_2}, \cdots ,{u_N}} \right\}$ 与物品集合 $\left\{ {\mathcal{V}{\rm{|}}{v_1},{v_2}, \cdots ,{v_M}} \right\}$ , 则图顶点集合为 $\mathcal{U} \cup \mathcal{V}$ . 图网络中存在两种非同质边缘, 第一种边表示用户与物品之间的交互关系, 即 $\left\{ {\mathcal{R}{\rm{|}}\mathcal{U} \times \mathcal{V}} \right\} = $ $ \{ \mathcal{R}|{r_{i,j}} : = \left( {{u_i},{v_j}} \right),{u_i} \in \mathcal{U},{v_j} \in \mathcal{V}\}$ , 描述了用户 ${u_i}$ 对物品 ${v_j}$ 进行过评价, 边 ${r_{i,j}}$ 的权重记为 $w_{i,j}^R$ , 表示用户 ${u_i}$ 对物品 ${v_j}$ 的评分量化分值, 边 ${r_{i,j}}$ 的时间戳记为 $t_{i,j}^R$ , 表示此次评分事件发生的时刻; 第二种边表示用户与用户之间的有向交互, 即 $\left\{ {\mathcal{S}{\rm{|}}\mathcal{U} \times \mathcal{U}} \right\} = \{ \mathcal{S}|{s_{i,j}} : = \left( {{u_i} \to {u_j}} \right),{u_i},{u_j} \in \mathcal{U}\}$ , 表示用户 ${u_i}$ 在社交平台上关注了用户 ${u_j}$ , 边 ${s_{i,j}}$ 的权重记为 $w_{i,j}^S$ , 表示用户 ${u_i}$ 与 ${u_j}$ 社交关系重要性的量化值, 本文不考虑社交网络的时序特征, 因此边 ${s_{i,j}}$ 无时间戳属性.

因此, 本文推荐系统可描述为: 给定用户集合 $\mathcal{U}$ 、物品集合 $\mathcal{V}$ , 以及评分边集合 $\mathcal{R}$ 、社交边集合 $\mathcal{S}$ , 经过一定的训练算法得到优化预测函数 $\mathcal{F}$ , 使得对于任意 ${u_i} \in \mathcal{U},{v_j} \in \mathcal{V},{r_{i,j}} \notin \mathcal{R}$ , 可预测用户 ${u_i}$ 对物品 ${v_j}$ 的评分 $\hat w_{i,j}^\mathcal{R} = \mathcal{F}\left( {{u_i},{v_j}} \right)$ , 作为是否推荐的依据. 以下将分别以用户节点与物品节点为中心, 展开介绍图网络局部图邻域聚合的具体算法细节.

2.1 图网络局部图邻域聚合

GNN中常用局部图邻域聚合技术^[8,19]来传递邻近节点之间的信息, 并迭代训练各节点的抽象表示. 对于给定图 $\mathcal{G}(\nu ,{\cal E})$ , 定义 $k$ 阶邻域函数 $Neig{h^k}\left( {{v_i}} \right) = \{ {v_k}|\left( {{v_i},{v_{i,1}}} \right), \cdots , $ $ \left( {{v_{i,k - 1}},{v_k}} \right) \in \mathcal{E}\} $ , 即 ${v_i}$ 与 ${v_k}$ 之间存在长度为k的路径. 本文采用一阶邻域函数, 简记为 $\mathcal{N}$ . 则GNN局部图邻域聚合算法可见算法1.

算法1. GNN局部图邻域聚合算法的第n次迭代

1) 遍历图 $\scriptstyle\mathcal{G}$ 的顶点 $\scriptstyle\mathcal{V}$ , 对每个顶点 $\scriptstyle{v_i}$ , 执行第2)~4)步操作;

2) 计算 $\scriptstyle{v_i}$ 的邻域节点集合 $\scriptstyle\mathcal{N}\left( {{v_i}} \right) = Neigh\left( {{v_i}} \right)$ ;

3) 利用聚合函数 $\scriptstyle Agg$ 计算 $\scriptstyle\mathcal{N}\left( {{v_i}} \right)$ 的聚合表示结果 $\scriptstyle {v}_{i}^{agg}=Agg\left(\mathcal{N}\left({v}_{i}\right)\right)$ ;

4) 将聚合结果 $\scriptstyle v_i^{agg}$ 与顶点自身 $\scriptstyle{v_i}$ 拼接, 并进行线性仿射与非线性激活, 得到该顶点本次迭代的表示 $\scriptstyle v_i^{\left( n \right)}$ .

上述算法中聚合函数 $Agg$ 有多种选择, 常见的如拼接、注意力、卷积等. 本文根据边 ${r_{i,j}}$ 存在时序性的特点, 选择基于注意力机制的门控循环单元作为邻域聚合函数, 以提取各节点邻域集合中的时序信息, 提高推荐系统对时序数据的学习能力.

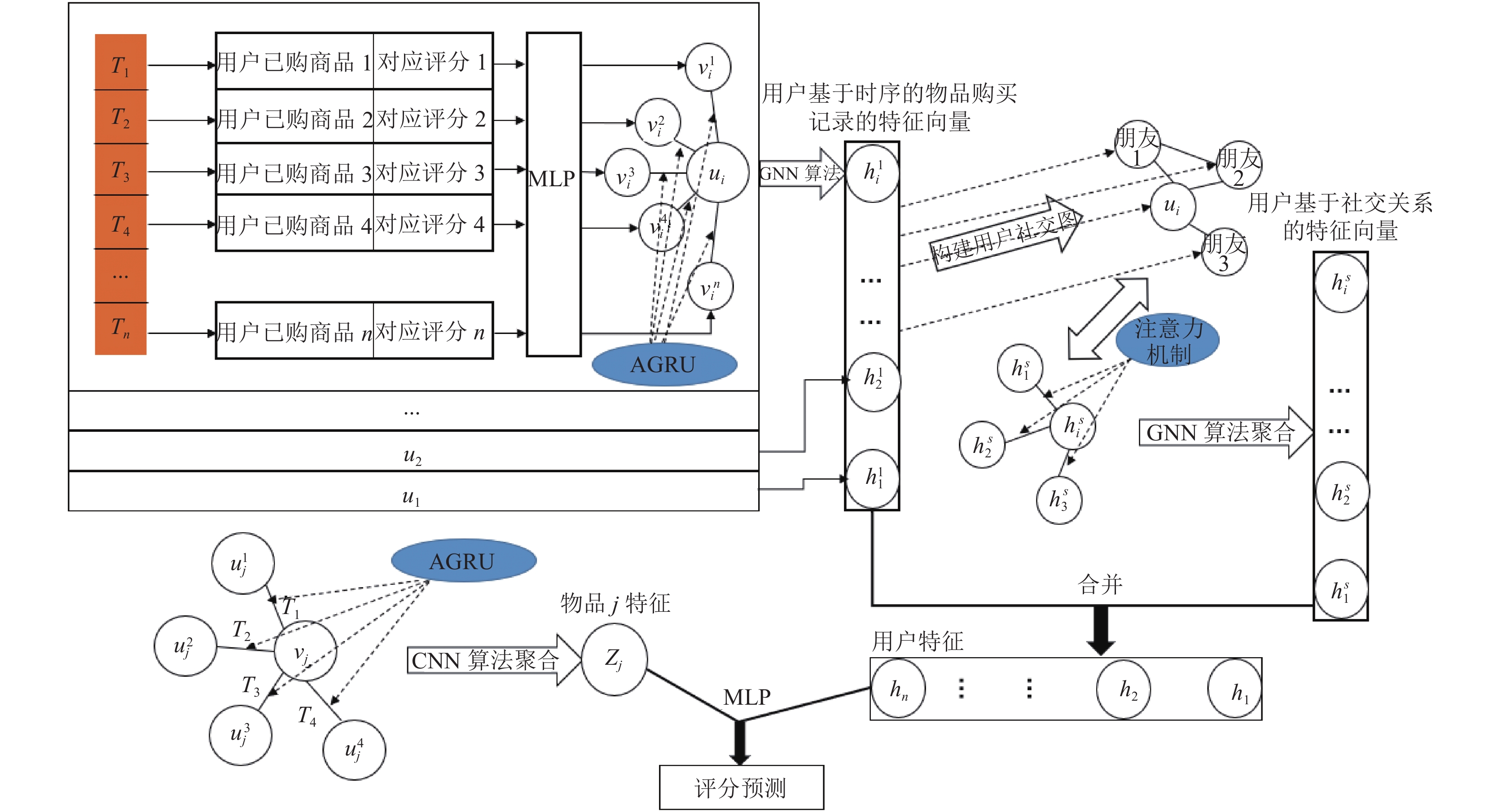
本文推荐系统图模型中(如图1所示), 顶点集合由用户集合 $\mathcal{U}$ 、物品集合 $\mathcal{V}$ 两部分组成, 边集合由评分关系集合 $\mathcal{R}$ 、社交关系集合 $\mathcal{S}$ 构成, 其中不包含关于物品集合 $\mathcal{V}$ 的闭集边集, 因此整个图可划分为3个局部图: 用户-物品图、用户-用户图以及物品-用户图, 以下将分别讨论其邻域聚合算法. 另外, 用户 ${u_i}$ 、物品 ${v_j}$ 分别通过嵌入层获得其向量表示 $e_i^\mathcal{U},e_j^\mathcal{V}$ ; 考虑到数据集中评分的取值为离散整数0–5, 权重 $w_{i,j}^\mathcal{R}$ 也通过对评分分值的嵌入向量表示, 即 $e_{i,j}^\mathcal{R}$ .

2.2 用户模型: AGRU聚合+社交影响力聚合

考虑图模型中的用户节点 ${u_i}$ 以及以其为端点的评分边 ${\mathcal{R}_{{u_i}}}$ 构成的局部图(图1左上角子图), 即用户-物品图. 则 ${u_i}$ 的邻域节点为用户 ${u_i}$ 所评价过的物品集合 ${\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right)$ , 根据各评分边的时间戳t, 可得到用户评分事件的时序排列. 为提取用户评价物品的时序特征, 本文在用户-物品图邻域聚合采用基于注意力的门控循环单元(Attention-GRU)来提取评分序列特征, 算法如算法2所示.

算法2. 用户-物品图AGRU聚合算法, 第n次迭代

1) 遍历用户集合 $\scriptstyle\mathcal{U}$ , 对每个顶点 $\scriptstyle{u_i}$ , 执行第2)~8)步操作;

2) 计算 $\scriptstyle{u_i}$ 在物品集合 $\scriptstyle\mathcal{V}$ 上的邻域节点集合 $\scriptstyle{\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right) = Neig{h^\mathcal{V}}\left( {{u_i}} \right)$ , 邻域节点数量 $\scriptstyle L = \left| {{\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right)} \right|$ ;

3) 将 $\scriptstyle{\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right)$ 中的物品节点 $\scriptstyle{v_j}$ 按时间戳 $\scriptstyle{t_{i,j}}$ 升序排列, 得到长度为L的物品序列 $\scriptstyle Seq\left( {{u_i}} \right) = \left[ {{v_1},{v_2}, \cdots ,{v_L}} \right]$ , 其中 $\scriptstyle {t_{i,1}} \le {t_{i,2}} \le \cdots \le {t_{i,L}}$ ;

4) 对序列 $\scriptstyle Seq\left( {{u_i}} \right)$ 中的每个物品元素 $\scriptstyle{v_j}$ , 查询其嵌入表示 $\scriptstyle e_j^\mathcal{V}$ , 以及对应评分 $\scriptstyle w_{i,j}^\mathcal{R}$ 的嵌入表示 $\scriptstyle e_{i,j}^\mathcal{R}$ ; 将 $\scriptstyle e_j^\mathcal{V}$ 与 $\scriptstyle e_{i,j}^\mathcal{R}$ 拼接输入多层感知机降维得到包含评分分值信息的物品表示 $\scriptstyle{e_j}^\prime $ ; 更新 $\scriptstyle Seq\left( {{u_i}} \right) = \left[ {{e_1}^\prime ,{e_2}^\prime , \cdots ,{e_L}^\prime } \right]$ ;

5) 将序列 $\scriptstyle Seq\left( {{u_i}} \right)$ 作为GRU的输入, 同时输入初始隐藏状态 $\scriptstyle{h_0}$ , 得到GRU在每个时刻末层输出构成的长度为L的序列 $\scriptstyle Outseq = \left[ {h_1^{\left( k \right)},h_2^{\left( k \right)}, \cdots ,h_L^{\left( k \right)}} \right]$ , 其中k为GRU的纵向堆叠层数;

6) 以GRU末层最后时刻的隐藏状态 $\scriptstyle h_L^{\left( k \right)}$ 为参考, 用注意力机制对 $\scriptstyle Outseq$ 中的L个元素进行加权平均得到 $\scriptstyle h'$ ;

7) 拼接 $\scriptstyle h'$ 与 $\scriptstyle h_L^{\left( k \right)}$ , 并经过线性层以及非线性ReLU激活, 得到 $\scriptstyle u_i^{agg}$ , 作为邻域集合 $\scriptstyle {\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right)$ 的聚合结果, 即 $\scriptstyle Agg\left({\mathcal{N}}^{\mathcal{V}}\left({u}_{i}\right)\right)={u}_{i}^{agg}$ ;

8) 将聚合结果 $\scriptstyle u_i^{agg}$ 与顶点自身嵌入表示 $\scriptstyle e_i^\mathcal{U}$ 拼接, 并进行线性仿射与非线性激活, 得到该用户节点第n次迭代的表示 $\scriptstyle u_i^{\left( n \right)}$ .

上述算法中, 第4)步采用双层感知机降维:

$\begin{array}{*{20}{c}} {x_j^{\mathcal{V}\mathcal{R}} = CONCAT\left( {e_j^\mathcal{V},e_{i,j}^\mathcal{R}} \right)} \end{array}$

(1)

$\begin{array}{*{20}{c}} {{y_j} = ReLU\left( {{W_1}x_j^{\mathcal{V}\mathcal{R}} + {b_1}} \right)} \end{array}$

(2)

$\begin{array}{*{20}{c}} {{e_j}^\prime = ReLU\left( {{W_2}{y_j} + {b_2}} \right)} \end{array}$

(3)

第5)步中第 $m = 1,2, \cdots ,k$ 层GRU^[20]在时刻 $t = 1, $ $ 2, \cdots ,L$ 执行下列计算:

$\begin{array}{l} {{x_t} = \left\{ {\begin{array}{l} {{e_t}^\prime ,\;\;m = 1} \\ {\delta _t^{\left( {m - 1} \right)} * h_t^{\left( {m - 1} \right)},\;\;m > 1} \end{array}} \right.} \end{array}$

(4)

$ r_{t}=\sigma\left(W_{i r} x_{t}+b_{\dot{r}^{r}}+W_{h r} h_{(t-1)}+b_{h r}\right) $

(5)

$ {\textit{z}}_{t}=\sigma\left(W_{i {\textit{z}}} x_{t}+b_{i {\textit{z}}}+W_{h {\textit{z}}} h_{(t-1)}+b_{h {\textit{z}}}\right) $

(6)

$\begin{array}{*{20}{c}} {{n_t} = \tanh \left( {{W_{in}}{x_t} + {b_{in}} + {r_t} * \left( {{W_{hn}}{h_{\left( {t - 1} \right)}} + {b_{hn}}} \right)} \right)} \end{array}$

(7)

$\begin{array}{*{20}{c}} {{h_t} = \left( {1 - {{\textit{z}}_t}} \right) * {n_t} + {{\textit{z}}_t} * {h_{\left( {t - 1} \right)}}} \end{array}$

(8)

其中, $\delta $ 表示Dropout函数, *表示Hadamard乘积, $ \sigma $ 表示Sigmoid激活函数:

$\begin{array}{*{20}{c}} {\sigma \left( x \right) = \dfrac{1}{{1 + {e^{ - x}}}}} \end{array}$

(9)

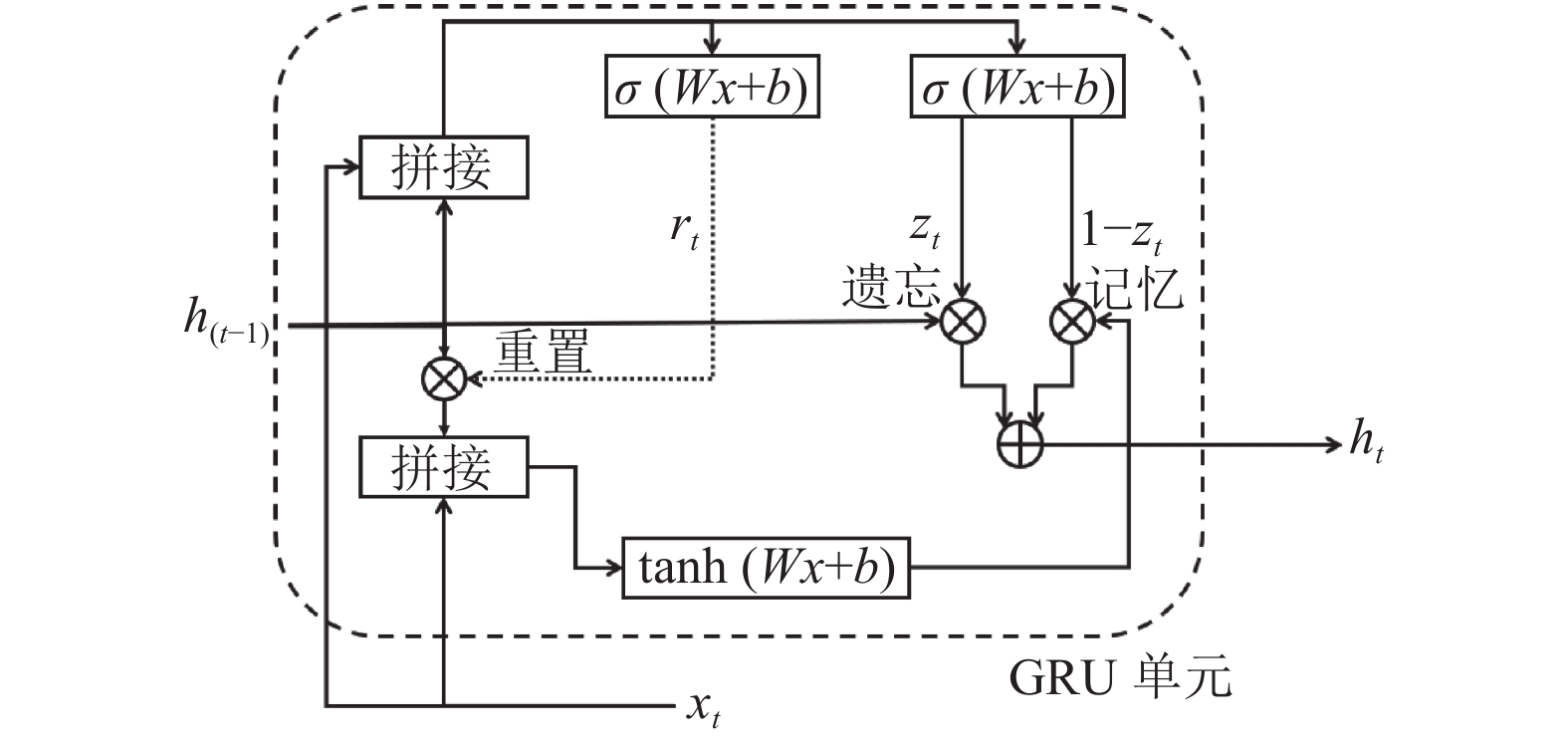
每个GRU单元的内部结构如图2所示, ${x_t}$ 表示当前时刻的输入, ${h_{\left( {t - 1} \right)}}$ 则表示该GRU单元上一时刻的隐藏状态. 两者拼接并分别通过独立全连接层得到重置因子 ${r_t}$ 和遗忘因子 ${{\textit{z}}_t}$ , 由于经过了Sigmoid激活, 两种因子的取值范围均在0到1之间. 重置因子对上一时刻的隐藏状态进行重置, 并将结果与当前输入拼接后传递给tanh激活的全连接层, 得到以当前输入为主、隐藏状态为辅的表示 ${n_t}$ . 另一方面, 遗忘因子 ${{\textit{z}}_t}$ 与记忆因子 $1 - {{\textit{z}}_t}$ 分别对 ${h_{\left( {t - 1} \right)}}$ 和 ${n_t}$ 调制, 实现了对序列历史隐含信息的选择遗忘以及当前输入的选择记忆.

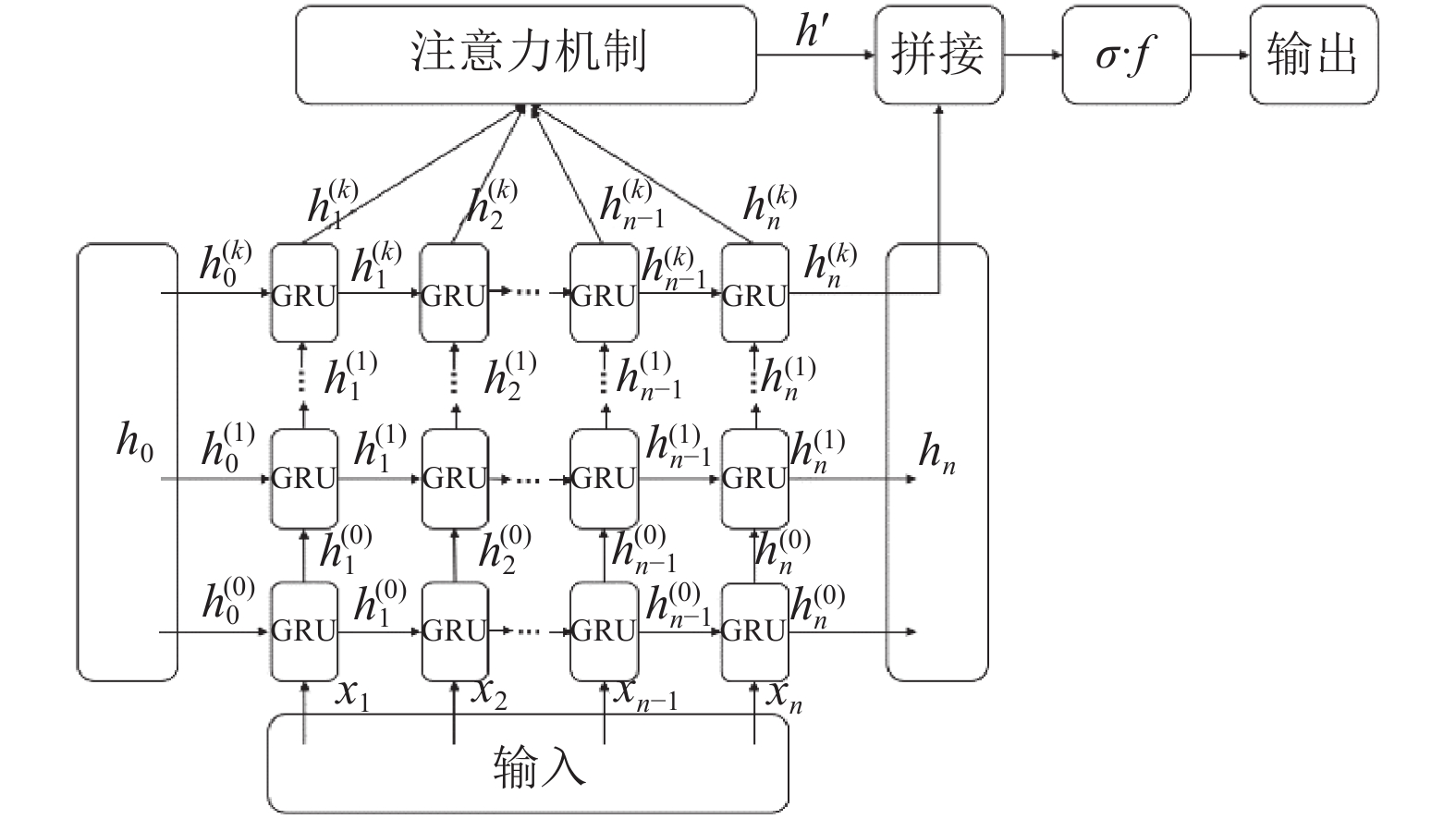
取GRU第k层的隐藏状态 $Outseq \!=\! \left[ {h_1^{\left( k \right)},h_2^{\left( k \right)}, \cdots ,h_L^{\left( k \right)}} \right]$ 作为输出, 并基于输出单元数量为1的多层感知机+Softmax实现注意力机制(如图3所示), 获得 $h_i^{\left( k \right)}$ 的注意力权重系数 ${p_i}$ :

$\begin{array}{*{20}{c}} {{x_i} = CONCAT\left( {h_i^{\left( k \right)},h_L^{\left( k \right)}} \right)} \end{array}$

(10)

$\begin{array}{*{20}{c}} {{y_i} = ReLU\left( {{W_{a1}}{x_i} + {b_{a1}}} \right)} \end{array}$

(11)

$\begin{array}{*{20}{c}} {{{\textit{z}}_i} = ReLU\left( {{W_{a2}}{y_i} + {b_{a2}}} \right)} \end{array}$

(12)

$\begin{array}{*{20}{c}} {{a_i} = ReLU\left( {{W_{a3}}{{\textit{z}}_i} + {b_{a3}}} \right)} \end{array}$

(13)

$\begin{array}{*{20}{c}} {{p_i} = \dfrac{{\exp \left( {{a_i}} \right)}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^L \exp \left( {{a_i}} \right)}}} \end{array}$

(14)

则邻域 ${\mathcal{N}^\mathcal{V}}\left( {{u_i}} \right)$ 聚合特征:

$ \begin{array}{c} Agg\left({\mathcal{N}}^{\mathcal{V}}\left({u}_{i}\right)\right)={u}_{i}^{agg}={\displaystyle \sum }_{i=1}^{L}{p}_{i}{h}_{i}^{\left(k\right)}\end{array}$

(15)

最终将邻域聚合特征与节点自身特征融合得到 $u_i^{\left( n \right)}$ :

$\begin{array}{*{20}{c}} {{x_i} = CONCAT\left( {u_i^{agg},e_i^\mathcal{U}} \right)} \end{array}$

(16)

$\begin{array}{*{20}{c}} {{y_i} = ReLU\left( {{W_1}{x_i} + {b_1}} \right)} \end{array}$

(17)

$\begin{array}{*{20}{c}} {u_i^{\left( n \right)} = ReLU\left( {{W_2}{y_i} + {b_2}} \right)} \end{array}$

(18)

另一方面, 考虑用户节点 ${u_i}$ 以及以其为起始端点的社交边 ${\mathcal{S}_{{u_i}}}$ 构成的局部图, 即用户-用户图(图1右上角子图). 本算法中社交边集为有向边集, 每条边表示用户的单向关注关系, 则 ${u_i}$ 的邻域节点为用户 ${u_i}$ 所关注的用户集合 ${\mathcal{N}^\mathcal{U}}\left( {{u_i}} \right)$ . 社交边 ${s_{i,j}}$ 的权重 $w_{i,j}^\mathcal{S}$ 量化为被关注者 ${u_j}$ 的影响力因子:

$\begin{array}{*{20}{c}} {w_{i,j}^\mathcal{S} = \left| {\left\{ {{u_k}|{u_k} \in \mathcal{U},{s_{k,j}} \in \mathcal{S}} \right\}} \right|} \end{array}$

(19)

在用户-用户局部图的邻域聚合的第n次迭代中, 使用用户-物品局部图第n次迭代聚合的结果 $u_i^{\left( n \right)}$ 作为节点 ${u_i}$ 的向量表示, 使得AGRU捕获到的时序特征也能够通过社交边进行传播. 具体聚合过程如下:

首先, 查询用户-物品图在用户集合 ${\mathcal{N}^\mathcal{U}}\left( {{u_i}} \right)$ 上的迭代结果得到:

$\begin{array}{*{20}{c}} {\left\{ {u_j^{\left( n \right)}|{u_j} \in {\mathcal{N}^\mathcal{U}}\left( {{u_i}} \right)} \right\}} \end{array}$

(20)

随后通过如式(10)–(14)所示的注意力网络得到 $u_i^{\left( n \right)}$ 关于其每个邻域节点的边权加权表示 $w_{i,j}^\mathcal{S}u_j^{\left( n \right)}$ 的注意力权重 ${p_j}$ . 则社交局部图的邻域聚合特征

$ \begin{array}{c} Agg\left({\mathcal{N}}^{\mathcal{U}}\left({u}_{i}\right)\right)={u}_{i}^{agg,\mathcal{S}}={{\displaystyle \sum }}_{j}{p}_{j}{w}_{i,j}^{\mathcal{S}}{u}_{j}^{\left(n\right)}\end{array}$

(21)

最终经过式(16)–式(18), 将 $u_i^{agg,\mathcal{S}}$ 与节点自身特征 $u_i^{\left( n \right)}$ 融合降维后得到 $u_i^{{{\left( n \right)}^*}}$ , 即为用户 ${u_i}$ 在第n次迭代后的最终向量表示.

2.3 物品模型: 对偶AGRU聚合

类似地, 考虑以物品节点为中心情形下的局部图邻域聚合算法. 由于评分边集 $\mathcal{R}$ 是无向边集, 因此物品-用户图(图1左下角子图)与用户-物品图完全对偶, 对于物品 ${v_i}$ , 其邻域用户集合 ${\mathcal{N}^\mathcal{U}}\left( {{v_i}} \right)$ 也可通过评分边的时间戳排序得到用户时间序列, 表示对物品 ${v_i}$ 评价过的用户在时间上的先后次序. 因此对于物品的特征迭代算法与算法2关于 $\left( {\mathcal{U},\mathcal{V}} \right)$ 对偶, 可对称地得到物品 ${v_i}$ 在第n次迭代后的表示 $v_i^{\left( n \right)}$ . 显然地, 物品社交图没有明显的物理意义, 因此物品模型中不包含自身社交影响力聚合, 用户 ${u_i}$ 在第n次迭代后的最终向量表示 $v_i^{{{\left( n \right)}^*}} = v_i^{\left( n \right)}$ . 当然, 用户社交的影响因素会在物品进行邻域聚合时传播给物品模型.

2.4 评分预测模型

根据第2.2、2.3节对用户 ${u_i}$ 、物品 ${v_i}$ 的AGRU聚合算法, 分别得到第 $n$ 次迭代后的向量表示 $u_i^{{{\left( n \right)}^*}},v_i^{{{\left( n \right)}^*}}$ . 将其拼接后经过单输出多层感知机(如图1右下角子图), 得到对评分关系 ${r_{i,j}}$ 权重(即评分分值)的预测值 $\hat w_{i,j}^\mathcal{R}$ .

在训练过程中, 以一个批次(batch)数据的均方误差MSE作为目标函数对模型中的参数进行优化:

$ MSE(\text { batch })=\frac{\displaystyle\sum_{k=1}^{b s i {\textit{z}} e}\left(\hat{w}_{i_{k}, j_{k}}^{\mathcal{R}}-w_{i_{k}, j_{k}}^{\mathcal{R}}\right)^{2}}{b { si{\textit{z}}e }} $

(22)

其中, $bsi{\textit{z}}e$ 为批次规模.

在推理过程中, 则 $\hat w_{i,j}^\mathcal{R}$ 即为推荐系统给出的用户 ${u_i}$ 对物品 ${v_i}$ 的评分分值预测.

3 实验结果与分析 3.1 数据集选取与预处理

实验采用Ciao数据集和Epinions数据集对算法进行验证, 两者均为包含社交关系信息的在线购物数据^[21]. 数据集包含两部分数据: (1)评分信息, 每条评分数据包括用户索引、物品索引、评分分值(0–5)以及时间戳4个维度; (2)社交信息, 每条社交数据包括关注者用户索引以及被关注者用户索引, 表示用户单向关注关系. Ciao数据集与Epinions数据集的特点如表1所示.

对数据集的预处理包括数据清洗、索引重映射、数据集切分、图建模、时间戳排序5个步骤. 数据清洗主要完成数据去重, 评分数据中包含少量重复评分边 ${r_{i,j}}$ , 根据其时间戳 $t_{i,j}^\mathcal{R}$ 保留较新的数据; 随后对数据集用户集合 $\mathcal{U}$ 、物品集合 $\mathcal{V}$ 分别进行索引重映射, 将原始索引映射至 $\left[ {1,2, \cdots ,\left| \mathcal{U} \right|} \right],\left[ {1,2, \cdots ,\left| \mathcal{V} \right|} \right]$ 范围内, 方便嵌入层映射; 之后将数据集中的评分边 $\mathcal{R}$ 集随机划分为训练评分边集 ${\mathcal{R}^{\rm train}}$ 和测试评分边集 ${\mathcal{R}^{\rm test}}$ , 分别比较训练集比重为60%和80%的实验结果; 对训练集和测试集, 分别建立第2节中描述的推荐图模型, 并对每个用户节点的邻域物品节点按时间戳提前排序, 则图网络迭代过程中无需重复排序, 以降低计算量, 对于物品节点的邻域用户节点, 也按同样方法提前排序.

3.2 评价指标

本文采用衡量推荐系统推荐效果的两个常用指标作为评判标准: 均方根误差RMSE和平均绝对误差MAE:

$ {RMSE}({y}, \hat{{y}})=\sqrt{\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}} $

(23)

$ {MAE}({y}, \hat{{y}})=\frac{1}{m} \sum_{i=1}^{m}\left|y_{i}-\hat{y}_{i}\right| $

(24)

其中, $y$ 表示测试集所有评分边的权重(真实值) $\left\{ {w_{i,j}^{{\mathcal{R}^{\rm test}}}} \right\}$ , $\hat y$ 则表示推荐系统对测试集各评分边的预测权重(预测值) $\left\{ {\hat w_{i,j}^{{\mathcal{R}^{\rm test}}}} \right\}$ . RMSE与MAE越小, 表明推荐系统预测的评分与真实值差距越小, 推荐效果越好.

3.3 对比模型

我们选取下列模型作为本算法对比的基准模型:

(1)概率矩阵分解(PMF)^[12]: 对用户潜在因子、物品潜在因子建模, 利用用户-物品评分概率矩阵进行推荐;

(2)社交推荐(SoRec)^[22]: 基于用户-物品评分矩阵提取联合潜在因子特征, 并结合社交矩阵进行推荐;

(3)社交矩阵分解(SocialMF)^[3]: 考虑了社交信任度在用户-物品评分矩阵分解空间中的传播;

(4)神经网络矩阵分解(NCF)^[23]: 将神经网络与矩阵分解结合进行推荐;

(5)深度社交网络推荐(Deep-SoR)^[24]: 利用深度神经网络对用户在社交关系中的特征进行训练, 并通过概率矩阵分解实现推荐;

(6)图网络推荐(GraphRec)^[9]: 根据社交关系和评分关系建立图网络, 利用注意力机制迭代图节点, 训练用户、物品的嵌入表示来实现推荐.

3.4 实验环境与超参数设置

本文采用Python 3.8, PyTorch 1.6, Cuda 10.2作为搭建算法的环境, 工作站CPU为4核Intel(R) Core(TM) i5-7500@3.40 GHz, GPU型号为NVIDIA GP102 [TITAN Xp].

本算法以batch为单位进行训练, 为了避免过拟合, 在各非线性激活函数输出端增加dropout层, 丢弃概率全局统一设置; 同时在图网络的每一批次迭代中, 对同一batch的用户、物品向量表示进行批次归一化. 算法中的超参数经过验证集(从训练集中抽取20%得到)反复调整得到: 嵌入维度(用户、物品、评分采用统一嵌入维度)为64, GRU纵向堆叠层数 $k = 2$ , dropout丢弃概率为0.5, 批次大小为64, 学习率为0.0005.

3.5 结果分析

本文在Ciao、Epionions数据集分别选取60%、80%作为训练集, 其余作为测试集对提出的算法进行了验证, 并与第3.3节列出的几种基准模型进行了对比,RMSE和MAE比较结果如表2.

从表2的结果可以看出, 本文所提出的基于AGRU-GNN算法在Ciao数据集和Epinions数据集上比表中所列的基准模型误差更小. 其中PMF和NCF只利用了用户与物品的评分数据, 而SoRec、SocialMF、Deep-SoR和GraphRec均使用了数据集中的社交关系数据, 因此平均比同类模型具有更小的误差. 本文所采用的AGRU聚合算法, 通过GRU对评分事件的时序信息提取, 并加以注意力机制对不同时刻的输出进行了有选择的加权平均, 结合社交局部图使得用户对物品的时变兴趣信息能够基于社交影响关系在用户之间传播, 从而达到了更好的推荐效果. 这证明了本文提出的算法在时序推荐数据集上具有一定的优越性.

我们还探究了不同超参数设置下, 对本文推荐算法效果的影响. 以Ciao(80%)数据集为例, 基准超参数的设置为GRU纵向堆叠层数 $k = 2$ , dropout概率为0.5, 迭代周期数为5. 图4展示了在基准超参数设置下, 模型预测误差随迭代周期数(epoch)的变化, 一次迭代周期表示图网络中所有顶点 $\mathcal{U} \cup \mathcal{V}$ 均被聚合迭代了一次. 可以看出模型的收敛速度较快, 5个周期后便达到了最优值, 随着迭代次数的增加, 模型出现了一定程度的过拟合. 收敛速度快得益于GRU对时序信息具有较强的表示能力, 快速地提取了用户、物品的时变特征; 另一方面, 由于GRU内部结构较为复杂, 也增大了模型的参数量, 因此随即出现了一定程度的过拟合现象.

GRU的层数一定程度上决定了模型的复杂程度, 为了避免严重的过拟合, 我们研究了不同GRU层数设置对模型误差的影响, 如图5. 可以看出, 双层GRU在此数据集上具有较好的推荐效果, 而层数过大则存在较严重的过拟合, 层数过小则削弱了模型对时序信息的学习能力.

为了更好地抑制过拟合, 模型中在大部分非线性激活单元的输出端以及GRU层间加入了dropout层, 并通过全局统一的dropout概率加以调节. 图6展示了模型最佳预测误差随dropout概率的变化, 以50%概率进行丢弃时, 模型在预测误差和过拟合之间达到了较好的平衡. 即使以较大的概率75%进行丢弃, 模型的功能依然没有受损, 但预测误差开始陡增.

另外, 我们还对比了本文模型的若干变种模型, 分别为:

(1) AGRU-GNN: 采用GRU作为图网络时序聚合模型, 并在物品-用户图、社交图的邻域聚合均采用了注意力机制, 即本文提出的最终模型;

(2) GRU-GNN: 禁用了模型中的注意力机制, 其余参数与(1)相同;

(3) ARNN-GNN: 采用Vanilla RNN作为图网络时序聚合模型, 也同时采用了注意力机制;

(4) GNN(即GraphRec^[9]): 基准图网络模型, 主要采用注意力聚合.

四种变种模型分别在Ciao(80%)和Epinions(80%)数据集上进行了对比, 结果如图7所示. GRU对时序信息的提取筛选能力明显优于普通RNN, 普通RNN对时序信息的选择记忆、遗忘能力不足, 导致ARNN-GNN的推荐有效性甚至弱于基准模型GraphRec; 另外, 注意力机制的存在也对模型整体性能有一定提升, 这说明注意力机制有助于在用户的物品交互时间序列关注重点事件, 同样地, 在社交图中也对不同的好友存在不同的关注权重.

综上所述, 本文提出的基于AGRU的图网络聚合算法, 在带有时间戳及社交信息的推荐数据集Ciao、Epinions上取得了良好的性能, 证明了本算法中采用的AGRU聚合从用户时序评价历史中提取了有效信息, 提升了推荐系统的准确度.

4 结论与展望

本文在图神经网络GNN架构的基础上, 基于推荐系统中评价事件的时序性以及用户特征、物品特征的时变特点, 提出了一种基于门控循环单元的注意力聚合算法. 通过Ciao、Epinions数据集, 证明了本算法在时序评价数据集上具有更低的预测误差, 说明用户的时变兴趣、物品的时变特征对于推荐系统也至关重要. GRU对于时间序列有较强的学习能力, 后续工作可考虑基于此算法实现推荐系统的在线训练, 即输入数据是随时间流动的流式数据, 图结构也随数据的增长动态变化, 使GRU从流式数据中捕获动态的时序特征, 以此实现推荐系统的在线演变和动态推荐. 在线的动态推荐更加接近实际生活中的推荐系统产品, 当然, 还需要解决冷启动、计算开销大甚至是分布式架构设计等问题.