作业车间调度问题的求解目标是得到一个科学、合理的调度方案. 一个科学、合理的调度方案能够有效提高生产效率、降低加工成本. 调度方案主要是确定各工件的加工次序和加工机器, 这是典型的NP-hard问题[1]. 现代企业间的竞争日趋激烈, 合理安排作业车间调度至关重要. 此外, 工业工程中车间生产规模逐渐扩大, 作业车间调度越来越复杂, 作业车间调度的组合改进问题已成为当今工业工程领域发展研究的热点问题之一[2]. 作业车间调度(JSP)都是凭借着工人的工作经验来安排工件的加工顺序, 然而这种方法不仅对工人要求较高, 且会出现安排不合理的情况. 启发式研究方法可以很好的解决这类问题, 常用的主流求解方法有粒子群优化算法、遗传算法、神经网络算法、禁忌搜索算法等[3-8]. 其中遗传算法(Genetic Algorithm, GA)作为一种群智能算法, 具有隐式并行性和全局搜索特性, 是求解作业车间调度问题的有力工具, 因此遗传算法被很多学者用来解决作业车间调度问题, 其在柔性作业车间(FJSP)的应用最为广泛. 根据FJSP的特点, 刘琼等[9]提出了一种改进的交叉变异方法并设计了一种初始解产生机制. 张国辉等[10]采用一种随机和优化相结合的初始化种群方法. 赵诗奎等[11]运用均匀设计原对遗传算法中的初始种群及适应度函数进行设计并将其应用到FJSP中. 对于上述3篇文献, 交叉和变异概率均是通过多次试验和前人经验给定, 没有采用自适应的方法确定. Kacem等[12]和Zhang等[13]分别提出了基于时间表和机器时间数组的机器指派法, 取得了较好的成效, 然而, 这两种方法都是基于单步优化指派机器, 最终的指派结果没有定量的全局性衡量指标, 不能保证最终机器指派结果的质量. 不同类型的作业车间所需的调度方法不同, 对于JSP, 何斌等研究了自适应交叉与变异概率提高了算法的寻优能力和收敛速度, 但其染色体总数仅根据初始种群数决定, 染色体多样性低[14]. 李春廷等通过改变遗传算法编码研究以及遗传算子的设计证明其算法的有效性, 但其实验时交叉、变异概率难以确定[15].
综上所述, 对于作业车间调度问题存在着染色体多样性低, 收敛速度慢, 遗传参数难以确定的问题. 对此本文提出了一种改进后的遗传算法来解决作业车间调度问题. 改进后的遗传算法在初始化时能够适当扩大种群, 在迭代过程中运用更易区分染色体的适应度函数计算染色体的适应度值, 并且运用能够自适应改变交叉和变异概率的算子调整概率值. 实验结果表明改进后的遗传算法更适用于作业车间调度.
2 车间调度问题描述在作业车间中有一批待加工工件, 这批待加工工件中有n个不同的工件, 每个工件均包含m道工序, 需要在m台机器上加工. 加工这批工件需要同时满足以下几点约束条件:
1) 所有工件的工序之间都有顺序约束, 即同一工件的各工序间有先后顺序, 需按照工序顺序进行加工;
2) 不同工件的加工工序之间没有顺序约束;
3) 每道工序只能在一台机器上加工;
4) 各工件工序的加工时间由对应的加工机器确定;
5) 在同一时刻车间中的同一机器只能加工一道工序;
6) 一道工序同一时刻只能在一台机器上加工, 且不能中途中断;
7) 不同工件之间优先级是相同的;
8) 不考虑机器故障等随机性因素.
本文求解目标为确定每台机器上工序的加工顺序和每个工序的开工时间, 使得最大完工时间 最小. 优化目标函数如式(1)所示:
| $ \min ({C_{\max }}),{C_{\max }} = \mathop {\max }\limits_{1 \le i \le m} \left\{ {\mathop {\max }\limits_{1 \le k \le n} \left( {{C_{ik}}} \right)} \right\} $ | (1) |
式中,
遗传算法的基因编码方式有很多种, 如浮点数编码、二进制编码、整数编码、符号编码、矩阵编码等[16]. 基因编码在算法中起着至关重要的作用, 编码的方式直接影响遗传算法的运行速度以及能否找到全局最优解[17]. 对于作业车间问题, 本文采用基于工序的实数编码来表示染色体[18], 一个编码后的染色体代表一个车间调度问题的调度方案.
对于n个不同工件在m台机器上加工的作业车间调度问题, 采用基于工序的编码方式编码后, 每条染色体均含有n×m个基因, 染色体的基因顺序对应所有工件工序的加工顺序, 即一条染色体代表一个车间调度问题的调度方案. 每条染色体的基因表示如下: 每个工件号在染色体中只能出现m次; 从染色体的第一个基因位到最后一个基因位依次遍历, 若同一工件号出现第k次则表示为此工件的第k道工序, 如染色体[3 3 2 1 2 1], 其中第一个3代表3号工件的第一道工序, 第二个3代表3号工件的第二道工序, 以此类推.
3.2 种群初始化首先给定种群的初始值p; 然后根据作业车间一道工序只在一台机器上加工的特点, 生成一个有n×m个基因的染色体; 最后调用randperm函数处理生成的染色体, 使其循环p次, 得到一个初始种群.
3.3 染色体适应度值本文的优化目标是最小化最大完成时间, 因此最大完成时间越小的染色体越优良. 染色体的适应度值是用来区分染色体间的优劣程度, 染色体越优良适应度值越大, 被选中的概率越大, 染色体越差适应度值越低, 被选中的概率越低. 为了更好的体现遗传算法优胜劣汰的准则, 本文采用新的计算染色体适应度值的方法, 使染色体间的区分度更加明显, 优良染色体被选中的概率大.
假设现有4个工件, 其加工完成时间分别为[20, 21, 22, 23], 利用取最大完成时间倒数方法得到的适应度值分别为[0.05, 0.0476, 0.0454, 0.0425], 改进后的算法得到的适应度值分别为[1,0.6308, 0.2923, 0]. 从这两组适应度值可看出, 这样设定适应度值可以让最大完成时间小的染色体被多次选择, 最大完成时间最大的染色体被少选择或者不被选择, 拉开了染色体间差距, 保障了对优良染色体的选择, 比前者获得优良染色体的概率更大.
适应度函数如式(2)所示, 最大完工时间的倒数如式(3)所示:
| $ f(i) = \frac{{h(i) - Min}}{{Max - Min}} $ | (2) |
| $ h(i) = \frac{1}{{{C_{\max }}}} $ | (3) |
式(2)、式(3)中, i为初始种群中的任意一条染色体, Max表示h(i)的最大值, Min表示h(i)的最小值.
在确定好各染色体的适应度值后在采用轮盘赌[19]的方法选择初始种群中的染色体.
3.4 交叉与变异交叉操作可以增加种群的多样性, 提高算法的搜索能力, 有利于产生优秀的染色体, 即有利于产生优秀的作业车间调度方案. 鉴于优先工序交叉法POX (Precedence Operation Crossover)能够很好地继承父代优良特征并且子代总是可行的这一特点, 本文选择POX进行交叉操作[20], 具体步骤如下所述:
步骤1. 按顺序依次选择种群中的一条染色体作为父代1即Parent1, 随机选择种群中的一条染色体作为父代2即Parent2;
步骤2. 将工件集{1, 2, 3, …, n}随机划分为两个非空子集j1, j2;
步骤3. 将Parent1和Parent2中包含
变异操作是小概率发生的, 它能够对染色体产生较小的扰动来增加种群的多样性, 从而产生更能满足目标函数要求的调度方案. 交叉后的染色体在进行小概率的变异操作, 可得到新的染色体, 保持种群多样性. 为了保证新得到的染色体编码是可调度的, 避免将不可行调度转换成可行调度, 减少代码运行时间, 本文采用互换法(Reciprocal Exchange Mutation, REM)进行变异操作[21]. 对一个染色体随机选择两个基因号, 将两个基因号上对应的工件号进行互换, 循环i次后可得到变异后的染色体.
3.5 交叉与变异概率交叉和变异概率影响着交叉操作和变异操作的发生, 当交叉和变异概率大于由rand函数在(0, 1)之间随机产生的值时, 染色体发生交叉、变异.
标准遗传算法的交叉和变异概率通常都是固定不变的值, 一般根据前人经验给定或者根据实验结果给定, 当给定的值较小时会使搜索范围变小, 不利于寻找更优解; 而当给定值较大时则可能导致已有的优良染色体在交叉和变异操作后变差; 在实验中容易出现早熟问题, 即未成熟收敛. 本文确定交叉和变异概率值时采用文献[22]提出的自适应改变交叉和变异概率的方法, 该算法能够在种群进化初期提高进化能力, 降低陷入局部最优的风险, 避免早熟问题的出现, 解决了参数难以确定的问题. 自适应交叉概率函数如式(4)所示, 自适应变异概率函数如式(5)所示:
| $ {P_c} = \left\{ {\begin{array}{*{20}{l}} {{k_1} - \dfrac{{{k_1}\left( {{g'} - {g_{\rm avg}}} \right)}}{{{g_{\max }} - {g_{\rm avg}}}},}&{{g'} > {g_{\rm avg}}}\\ {{k_2},}&{{g'} \le {g_{\rm avg}}} \end{array}} \right. $ | (4) |
| $ {p_m} = \left\{ {\begin{array}{*{20}{l}} {{k_3} - \dfrac{{{k_3}(g - {g_{\rm avg}})}}{{{g_{\max }} - {g_{\rm avg}}}},}&{g > {g_{\rm avg}}}\\ {{k_4},}&{g \le {g_{\rm avg}}} \end{array}} \right. $ | (5) |
式(4)、式(5)中,
程序运行平台为MacOS10. 13.6操作系统上的Matlab_R2018a软件, 用标准遗传算法和改进算法分别对测试用例库中的FT06和LA01这两个用例进行实验. FT06是一个6×6的测试用例, 即共有6个工件, 每个工件都有6个加工工序, FT06的工件工序集J=[3, 1, 2, 4, 6, 5; 2, 3, 5, 6, 1, 4; 3, 4, 6, 1, 2, 5; 2, 1, 3, 4, 5, 6; 3, 2, 5, 6, 1, 4; 2, 4, 6, 1, 5, 3]; 加工FT06各个工序所需时间集T=[1, 3, 6, 7, 3, 6; 8, 5, 10, 10, 10, 4; 5, 4, 8, 9, 1, 7; 5, 5, 5, 3, 8, 9; 9, 3, 5, 4, 3, 1; 3, 3, 9, 10, 4, 1]; LA01是一个10×5的测试用例, 即共有10个工件, 每个工件都有5个加工工序, LA01的工件工序集J=[2, 1, 5, 4, 3; 1, 4, 5, 3, 2; 4, 5, 2, 3, 1; 2, 1, 5, 3, 4; 1, 4, 3, 2, 5; 2, 3, 5, 1, 4; 4, 5, 2, 3, 1; 3, 1, 2, 4, 5; 4, 2, 5, 1, 3; 5, 4, 3, 2, 1]; 加工LA01各个工序所需时间集T=[21, 53, 95, 55, 34; 21, 52, 16, 26, 71; 39, 98, 42, 31, 12; 77, 55, 79, 66, 77; 83, 34, 64, 19, 37; 54, 43, 79, 92, 62; 69, 77, 87, 87, 93; 38, 60, 41, 24, 83; 17, 49, 25, 44, 98; 77, 79, 43, 75, 96].
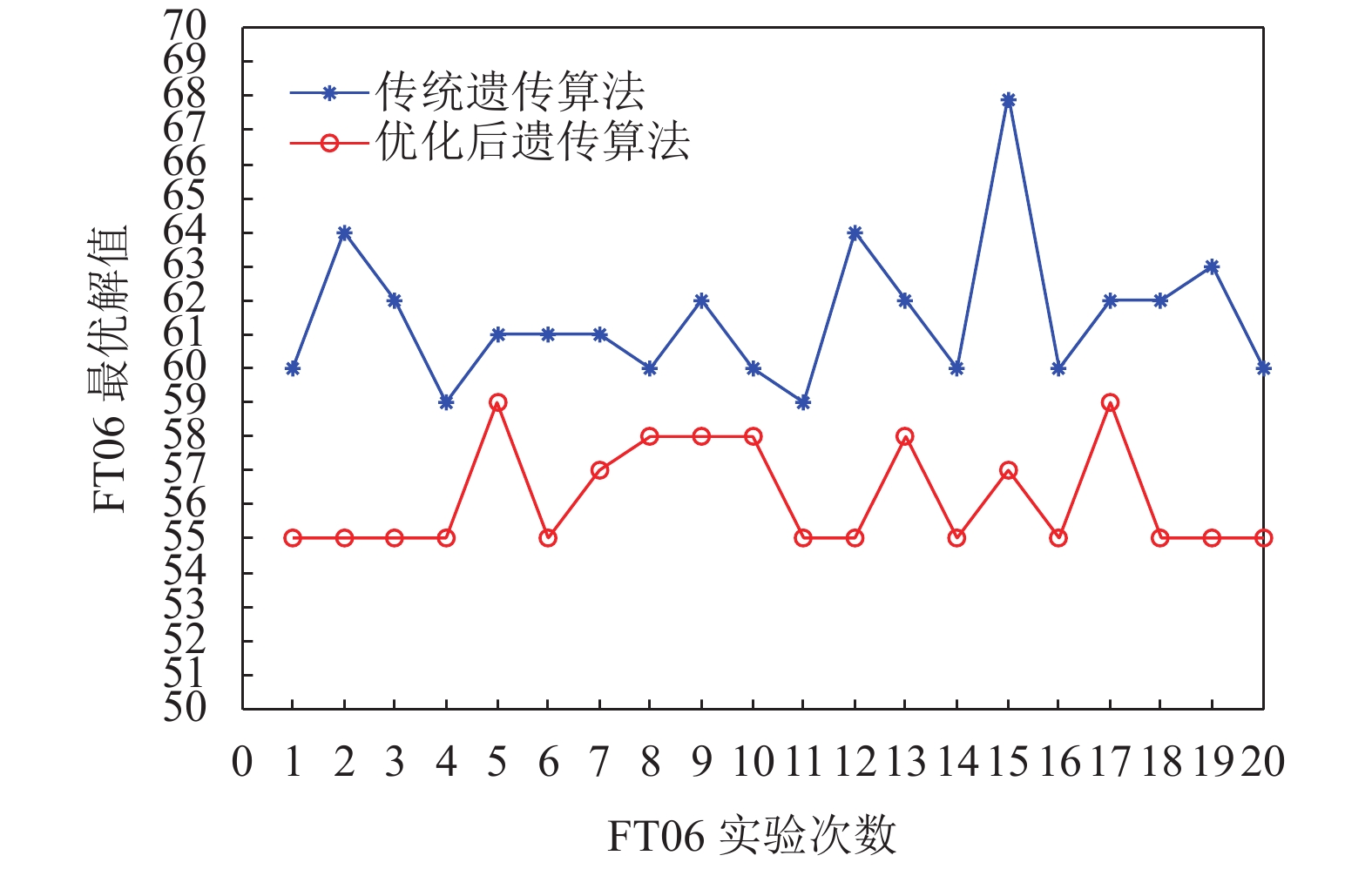
此次实验涉及到标准遗传算法和对标准遗传算法的种群初始化, 适应度函数, 交叉、变异概率的确定进行优化后得到的遗传算法. 根据多次实验以及前人实验结果, 标准遗传算法的参数设置为: 迭代次数为200, 种群总大小为100, 交叉概率为0.9, 变异概率为0.05; 改进后的遗传算法参数设置为: 迭代次数为200, 种群总大小为100, 在初始化时将种群总大小扩大为原来的2倍, 以增加染色体的多样性, 并且由于改进算法中交叉和变异概率是自适应调节的, 无需直接指定, 由式(4)和式(5)确定, 优化后的遗传算法参数设置为迭代次数为200, 种群总大小为100, k1=k2=0.9, k3=k4=0.1. 运行20次后, 图1和图2分别为使用标准遗传算法与改进后的遗传算法求解FT06和LA01得到的最优解值.
从图1和图2中可知, 在20次实验中, 改进后的遗传算法得到的最优解都优于标准遗传算法得到的最优解, 证明改进后的遗传算法的寻优能力强于标准遗传算法. 分析总结图1、图2中的数据, 结合每次实验得到的迭代过程图, 得到结果对比表如表1所示.
|
图 1 FT06基准案例最优解 |

|
图 2 LA01基准案例最优解 |
| 表 1 基准案例(FT06, LA01)结果对比表 |
从表1可看出, 用FT06基准案例验证时, 标准算法求得的最优解为59, 20次实验中有2次求得59, 所得解均值是61.5, 当求得最优解为59时, 最优迭代次数为3, 平均迭代次数为11.6; 改进算法求得的最优解为55, 20次实验中有12次求得55, 所得解均值为56.2, 当求得最优解为55时, 最优迭代次数为10, 平均迭代次数为38.05; 用LA01基准案例验证时, 标准算法求得的最优解为740, 20次实验中有1次求得740, 所得解均值为774.35, 当求得最优解为740时, 最优迭代次数为4, 平均迭代次数为8.4; 改进算法求得的最优解为666, 20次实验中有14次求得最优解, 最优解平均值为671.3, 当求得最优解为666时, 最优迭代次数为18, 平均迭代次数为76.6.
由此可以看出, 改进后的遗传算法得到的最优解优于标准遗传算法, 解决了标准算法的早熟问题; 同时在进行20次实验后, 改进后的算法得到最优解的次数分别为12和14次大于标准算法得到最优解的次数, 解决了标准算法的解的稳定性差问题.
运用标准遗传算法对不同基准案例进行验证时, 可能需要不同的交叉和变异参数来提高算法的收敛速度和搜索能力. 而交叉和变异概率难以确定, 一般由实验经验或者参考前人的参数设计给出, 给定后的值固定不变. 对于标准遗传算法只改进适应度函数后进行实验验证, 给定交叉概率为0. 9, 变异概率为0. 05, 实验结果如表2所示.
| 表 2 改进适应度函数后的实验结果表 |
对比表1, 表2可知, 表2中迭代次数均大于表1中本文算法对应的迭代次数. 由此可知, 改进算法中的自适应交叉和变异概率提高算法的收敛速度.
由参考文献[23]可知, FT06的最优解为55, LA01的最优解为666. 结合结果分析可知, 不论是FT06基准案例还是LA01基准案例, 改进算法均能得到与基准案例最优解相同的解, 并且在20次实验中, 改进算法得到最优解的次数分别为12和14次, 均高于标准算法; 改进算法在得到最优解时, 其迭代次数分别为10和18, 相比于只改进寻优能力后得到的最优解时的迭代次数, 改进算法可以提高收敛速度.
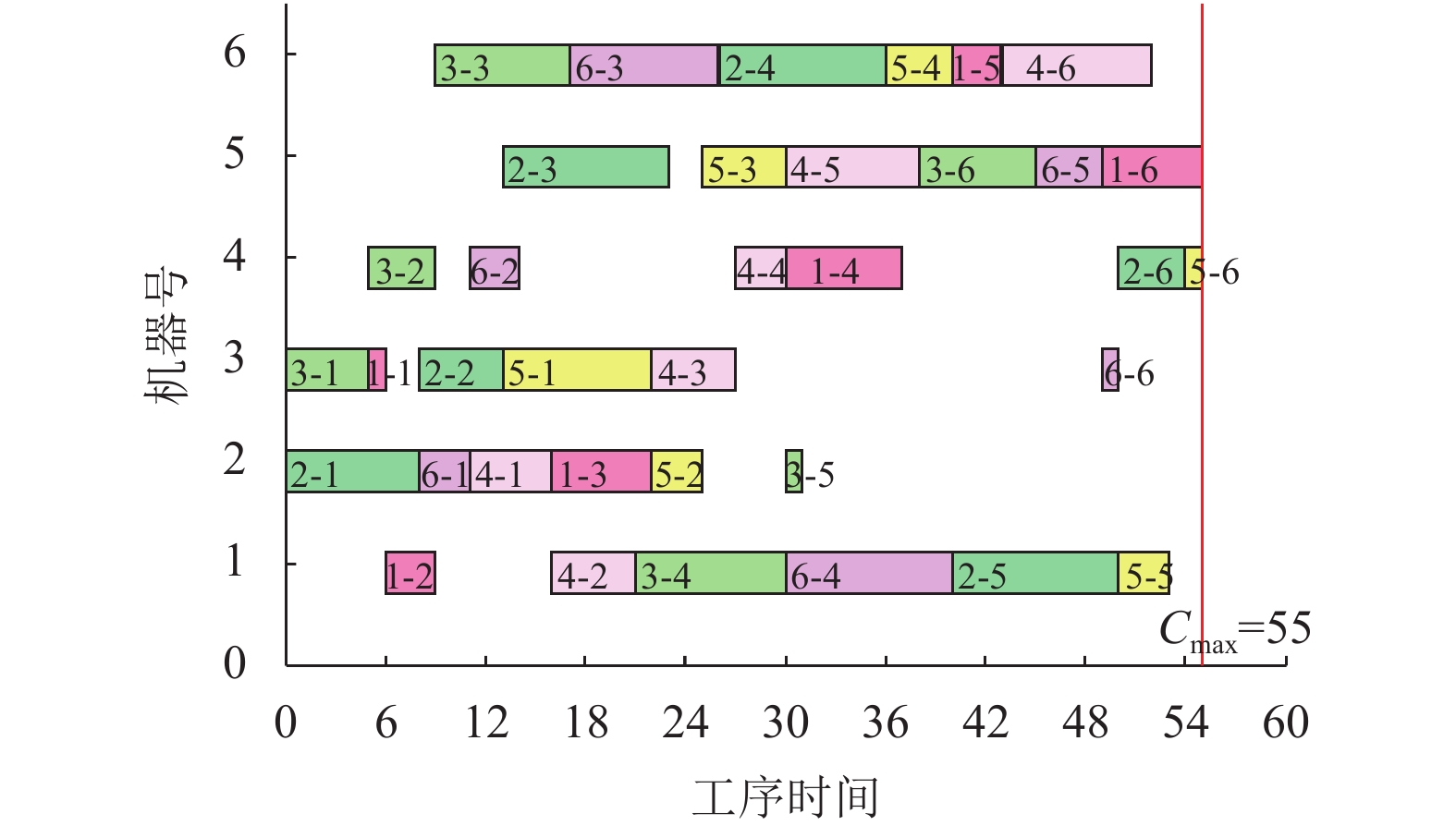
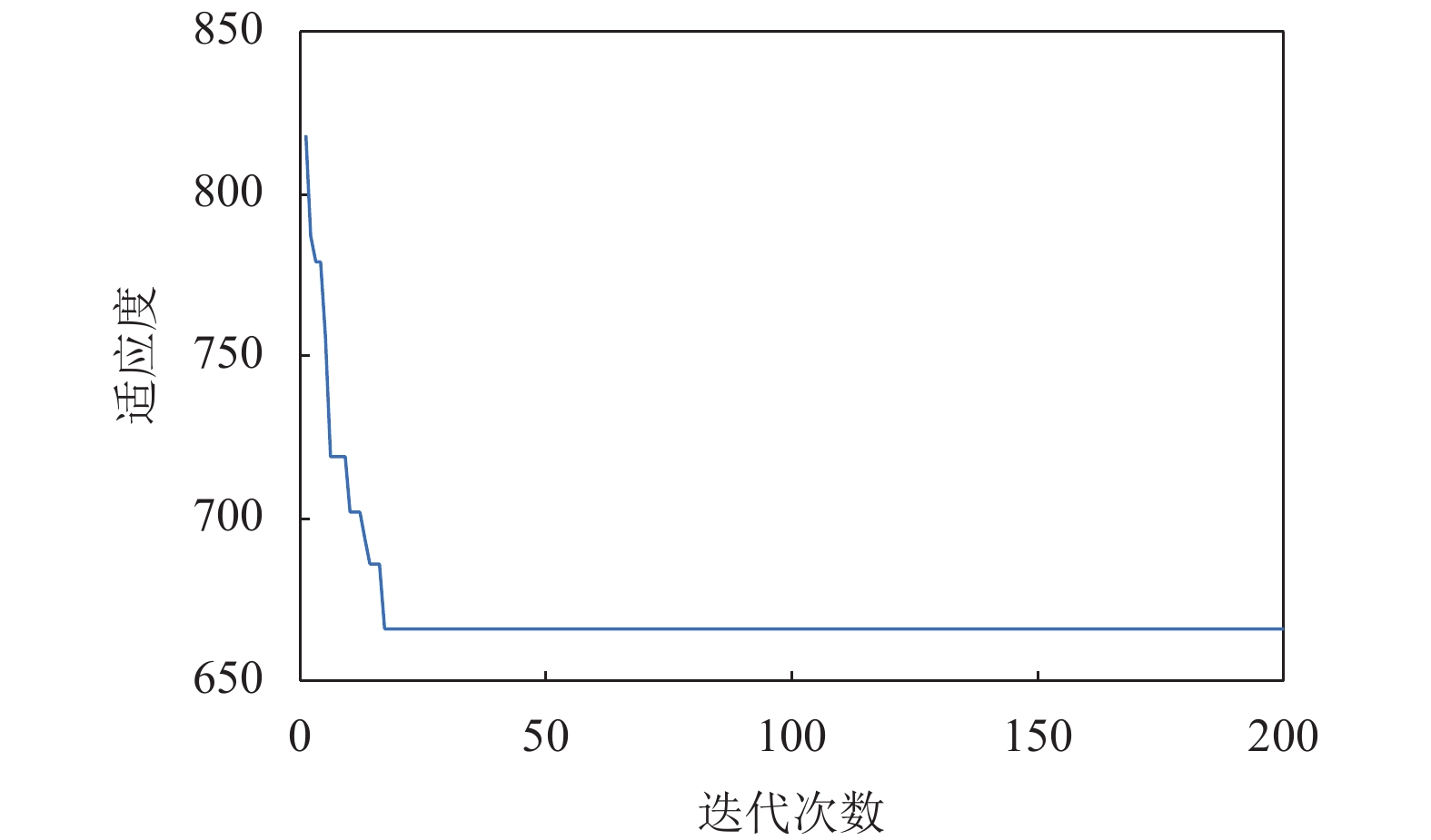
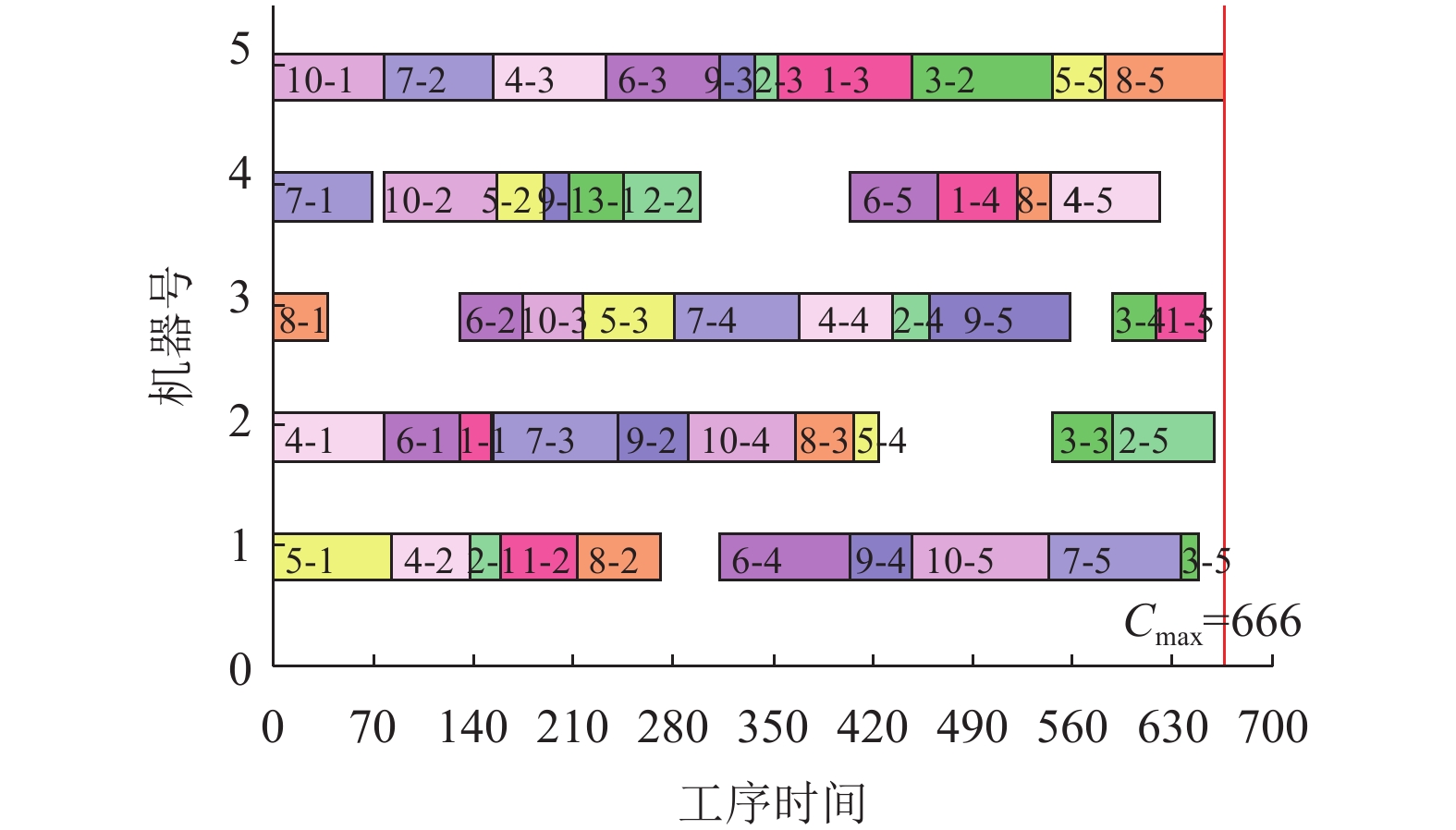
用FT06和LA01验证改进后的遗传算法, 生成的遗传代数图和甘特图分别如图3~图6所示. 由图4可知每台机器上的工序顺序, 以及加工完所有工件花费的最少加工时间55, 由图3可知得到此调度方案只迭代了10次; 由图6可知每台机器上的工序顺序, 以及加工完所有工件花费的最少加工时间666, 由图5可知得到此调度方案只迭代了18次. 仿真结果表明改进后的遗传算法比标准遗传算法收敛速度快, 所得解更稳定, 遗传参数较易确定. 相较于文献[14,15], 优化后的遗传算法的收敛速度更优, 交叉和变异概率采用自适应交叉、变异函数确定, 解决了参数难以确定的问题, 证实了改进后遗传算法的有效性和可靠性.

|
图 3 FT06遗传代数图 |
|
图 4 FT06甘特图 |
|
图 5 LA01遗传代数图 |
|
图 6 LA01甘特图 |
5 结束语
以最小化最大完成时间为优化目标, 对标准遗传算法进行改进, 以求解目标问题的最优解. 在初始化时扩大种群数量以增加种群多样性, 采用的适应度函数可以增加染色体区分度, 使用POX算法完成交叉操作, 产生的子代可以很好地继承父代优良特征并且子代总是可行, 交叉和变异概率采用自适应交叉和变异概率, 概率可根据染色体适应度值自动调整. 通过对FT06和LA01进行仿真实验, 所得的实验结果表明改进后的遗传算法解决了标准遗传算法中参数难以确定, 早熟收敛, 所得解不稳定的问题, 提高算法的寻优能力和收敛速度, 比标准遗传算法更适用于作业车间生产. 对于柔性作业车间调度问题, 其每道工序可以在多台机床上加工, 并且在不同的机床上加工所需时间不同, 因此本文算法不适用于柔性作业车间的调度问题, 下一步将研究能够处理柔性作业车间的调度问题.
| [1] |
徐华, 程冰. 混合遗传蝙蝠算法求解单目标柔性作业车间调度问题. 小型微型计算机系统, 2018, 39(5): 1010-1015. DOI:10.3969/j.issn.1000-1220.2018.05.026 |
| [2] |
曹磊, 叶春明, 黄霞. 变邻域杂草算法在多目标柔性作业车间调度中的应用. 计算机应用研究, 2018, 35(1): 150-154, 165. DOI:10.3969/j.issn.1001-3695.2018.01.031 |
| [3] |
Ariyasingha IDID, Fernando TGI. A performance study for the multi-objective ant colony optimization algorithms on the job shop scheduling problem. International Journal of Computer Applications, 2015, 132(14): 1-8. DOI:10.5120/ijca2015907638 |
| [4] |
Florez E, Gomez W, Lola B. An ant colony optimization algorithm for job shop scheduling problems. International Journal of Artificial Intelligence & Applications, 2013, 4(4): 53-66. |
| [5] |
Peng B, Lu ZP, Cheng TCE. A tabu search/path relinking algorithm to solve the job shop scheduling problem. Computers & Operations Research, 2015, 53: 154-164. |
| [6] |
Spanos AC, Ponis ST, Tatsiopoulos IP, et al. A new hybrid parallel genetic algorithm for the job-shop scheduling problem. International Transactions in Operational Research, 2014, 21(3): 479-499. DOI:10.1111/itor.12056 |
| [7] |
Nasiri MM. A modified ABC algorithm for the stage shop scheduling problem. Applied Soft Computing, 2015, 28: 81-89. DOI:10.1016/j.asoc.2014.12.001 |
| [8] |
Karimi-Nasab M, Modarres M, Seyedhoseini SM. A self-adaptive PSO for joint lot sizing and job shop scheduling with compressible process times. Applied Soft Computing, 2015, 27: 137-147. DOI:10.1016/j.asoc.2014.10.015 |
| [9] |
刘琼, 张超勇, 饶运清, 等. 改进遗传算法解决柔性作业车间调度问题. 工业工程与管理, 2009, 14(2): 59-66. DOI:10.3969/j.issn.1007-5429.2009.02.011 |
| [10] |
张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题. 机械工程学报, 2009, 45(7): 145-151. |
| [11] |
赵诗奎, 方水良, 顾新建. 柔性车间调度的新型初始机制遗传算法. 浙江大学学报(工学版), 2013, 47(6): 1022-1030. |
| [12] |
Kacem I, Hammadi S, Borne P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2002, 32(1): 1-13. DOI:10.1109/TSMCC.2002.1009117 |
| [13] |
Zhang GH, Gao L, Shi Y. An effective genetic algorithm for the flexible job-shop scheduling problem. Expert Systems with Applications, 2011, 38(4): 3563-3573. DOI:10.1016/j.eswa.2010.08.145 |
| [14] |
何斌, 张接信, 张富强. 一种求解作业车间调度问题的改进遗传算法. 制造业自动化, 2018, 40(8): 113-117. DOI:10.3969/j.issn.1009-0134.2018.08.029 |
| [15] |
李春廷. 基于遗传算法的作业车间调度问题研究[硕士学位论文]. 秦皇岛: 燕山大学, 2007.
|
| [16] |
张国辉, 吴立辉. 求解柔性作业车间调度的GATOC混合方法. 计算机工程与应用, 2015, 51(23): 266-270. DOI:10.3778/j.issn.1002-8331.1502-0171 |
| [17] |
王雷, 蔡劲草, 李明. 基于正交试验的遗传算法参数优化. 工程技术版, 2016, 16(2): 81-85. |
| [18] |
玄登影, 王福林, 高敏慧, 等. 一种改进适应度函数的遗传算法. 数学的实践与认识, 2015, 45(16): 232-238. |
| [19] |
李兢尧, 黄媛, 王军强, 等. 求解扩展双资源约束作业车间调度的分支种群遗传算法. 西北工业大学学报, 2016, 34(4): 634-640. DOI:10.3969/j.issn.1000-2758.2016.04.013 |
| [20] |
张雪艳, 梁工谦, 董仲慧. 基于改进自适应遗传算法的柔性作业车间调度问题研究. 机械制造, 2016, 54(6): 1-4, 33. DOI:10.3969/j.issn.1000-4998.2016.06.001 |
| [21] |
黄俊生, 广晓平. 关于生产车间作业优化调度效率仿真研究. 制造业自动化, 2017, 39(10): 95-99. DOI:10.3969/j.issn.1009-0134.2017.10.022 |
| [22] |
郑先鹏, 王雷. 面向作业车间调度问题的遗传算法改进. 河北科技大学学报, 2019, 40(6): 496-502. DOI:10.7535/hbkd.2019yx06006 |
| [23] |
王明. 基于改进遗传算法的作业车间调度问题研究[硕士学位论文]. 芜湖: 安徽工程大学, 2019.
|
 2021, Vol. 30
2021, Vol. 30



