流程工业也被称为过程工业(process industry), 包括化工、食品、制药、冶金、造纸等生产行业, 是我国先进生产力发展的重要支柱. 早期的过程工业通常是连续型过程, 即从原料投入到产品制成是依次连续进行的, 常见于冶金、炼钢、玻璃制品等大规模生产行业. 随着科学技术的迅速发展和人民生活水平的提高, 市场竞争对流程工业的压力不断增大, 而大数据、人工智能、云计算等技术的出现, 也给流程工业带来了翻天覆地的变化[1], 小批次、多品种生产过程的日益增加促使连续型生产过程向间歇型生产过程转化, 其中以化工、生物制药和食品饮料等行业尤为典型.
间歇生产过程是指将有限量的物质按规定的加工顺序在一个或多个加工设备中加工以获得有限量产品的加工过程(ANSI/ISA-88.01标准)[2]. 间歇生产过程具有动态性和间断性, 为了满足精细化生产需求, 可以在一个多功能、多用途的生产设备上, 生产出不同种类的产品. 与连续生产过程相比, 间歇生产过程的特性可以用“多重时变”来概括[3]:
(1)多: “多样产品”, 指同一台设备可以生产不同材质、形状、大小的产品, 当产品切换后, 生产操作条件改变, 潜在过程特性随之变化.
(2)重: “重复运行”, 指不断地重复同一操作来生产多件产品.
(3)时: “时段切换”, 指在不同的时段运行不同的生产操作.
(4)变: “变换指标”, 指在不同的生产阶段, 决定产品的关键变量发生变化, 控制目标和控制方案也会随之变化.
间歇生产过程的“多重时变”特性导致不同产品、不同生产阶段需要有不同的操作工艺或不同的生产目标, 因此, 要保证生产过程的产品质量, 亟需提出有效的间歇生产过程的优化方法. 间歇生产过程的优化方法的研究一般可以分为生产工艺的优化研究、调度优化的研究以及生产单元的优化研究等, 其中针对生产单元的优化较为广泛, 本文也是仅对单元优化方法进行了总结.
从系统控制的角度来看, “多重时变” 的特性也导致间歇生产过程具有非稳态工作点, 且随着批次的更迭在有限时间内重复运行. 非稳态工作点, 即所有参数(如温度、流量等)目标值呈现曲线变化, 使被控对象输入输出关系不断改变, 工作点反复发生切换, 系统动态呈现出很强的非线性特点. 没有稳态工作点使得间歇生产过程无法建立精确的过程模型, 给间歇生产过程的控制带来了很多困难, 也给高质量精细化生产带来了新的挑战. 因此, 为了减少能耗和时间、增加收益, 探索间歇生产过程中的优化方法和控制策略成为热点.
优化与控制是间歇生产过程高质高效运行的重要手段. 间歇生产过程中的优化问题可以分为开环形式以及闭环形式[4]. 开环形式的间歇生产过程优化基于机理模型对经济性能指标进行优化从而获得开环操作轨迹, 并将开环操作轨迹直接作用到间歇生产过程[5]. 但因为过程的不确定性, 需要修改这个开环解. 针对过程的不确定性, 闭环形式优化则是基于过程测量在线求解开环形式的优化问题, 通常需要在线求解大规模复杂非线性优化问题[6], 该问题通常需要大量的计算成本和计算时间. 间歇生产过程控制则是对优化获得的操作轨迹的跟踪, 即在有不确定性干扰的条件下, 使实际操作轨迹尽可能贴近最优操作轨迹[7]. 本文将分别从间歇生产过程的优化和控制两个方面进行讨论.
1 间歇生产过程优化策略 1.1 离线优化传统优化是开环形式, 根据静态模型或经验模型, 在离线的状态下采用数值计算的方法来求解优化问题, 从而得到相关控制变量的操作轨迹. 文献[8]针对造纸厂蒸煮过程, 设计了一套基于集散控制系统(Distributed Control System, DCS)的间歇蒸煮过程模型, 通过解析方法实现对木浆卡伯值的精确预报及升温曲线的优化. 文献[9]针对甲醛生产建立反应过程数学模型, 在满足产品质量和产量的约束条件下, 通过优化计算求得了使原料单耗最低的最优操作条件. 文献[10]针对乳液聚合反应器的机理模型难以建立问题, 基于递归神经网络和以往操作经验建立了反应器的数学模型, 采用序贯二次规划法计算最优反应温度并实施控制, 使生产效率大大提高, 节省了建模时间.
此类优化方法一般在生产开始之前, 通过解析法或数值法在离线的情况下计算出过程参数, 得到最优开环轨迹, 无法预测到过程中的不确定因素, 也无法避免由初始条件变化来的影响, 因此现在研究的较少.
1.2 在线优化在线优化是利用测量传感技术不断在线获取研究对象的测量数据, 用获得的数据更新原来的过程模型, 从而克服过程干扰带来的模型偏移、失配问题. 根据获取在线测量数据的方法的不同, 在线优化方法主要分为基于在线辨识的重复优化法和级联优化法.
基于在线辨识的重复优化法是将间歇生产过程分割成若干段连续过程, 分别对每段连续过程用解析法或数值法计算优化解. 李春富等针对异丁烯酸甲酯聚合反应过程, 运用部分最小二乘法(Multiway Partial Least Squares, MPLS)建立软测量模型, 通过在线测量过程变量对产品质量进行预测[11]. 但这种方法仅适用于线性过程, 不宜用于复杂的非线性过程. 针对非线性问题, 李春富团队[12]又利用径向基神经(Radial Basis Function, RBF)网络的万能逼近性来处理过程的非线性, 将递推最小二乘(Recursive Partial Least Squares, RPLS)算法同RBF网络结合, 根据在线测量的数据自适应地调整过程模型的结构和参数, 使模型适应非线性过程的变化.
间歇生产过程很多时候要涉及高维优化问题, 因为间歇生产过程的时变性造成了过程模型一般是由多个线型模型组成. 此外, 该优化策略还存在两个不足, 一是辨识需要额外的激励信号, 易使系统的稳定性变差, 并且当状态变量存在扰动时计算量过大; 二是该优化策略需要状态变量全部可测, 对存在不可测扰动的过程优化效果欠佳.
级联优化方法结合了离线优化和反馈控制的优点, 图1为级联优化的系统结构图, 需要嵌套两个PI控制器组成反馈模型. 内环采用普通控制器, 用来跟踪给定值, 而外环为内环的控制器提供最优设定值轨迹. 当外环被触发, 就开始修正设定值轨迹, 使设定值不断接近最优值[13]. 文献[14]将球磨机简化为一个连续控制过程, 采用连续磨矿采样数据确定参数, 将自适应律和RBF算法相结合, 再利用改进的RBF算法优化被控对象, 实验证明, 优化后跟踪轨迹更加逼近理想状态. 与在线辨识的重复优化相比, 该策略的优点是不需要过程状态完全可测, 节约时间. 但该策略的缺点是对存在非线性的过程的优化效果欠佳.

|
图 1 级联优化的系统结构图 |
近年也提出了很多基于在线测量值的实时优化,如动态规划、离散化和参数化法, 主要是针对含复杂约束的间歇生产过程的过程参数和质量参数进行在线监测, 利用监测获得的数据不断更新过程模型. 文献[15]采用几何法求解间歇过程的优化问题, 在状态空间变量复杂多样的情况下, 引入反馈律求解终端优化问题. 文献[16]使用最速梯度法解决间歇过程的模型失配问题, 基于状态估计模型在线修改设定值, 调节最优轨线的过程参数, 利用实时观测器控制设定值曲线. 实时优化中常使用的方法是动态优化和非线性优化, 但需要大量的计算成本以及计算时间, 这限制了更新的频率, 导致实时更新受到限制.
根据优化是否基于模型, 将实时优化分为基于模型的实时显性优化和实时隐性优化[17].
(1)基于模型的显性优化方法, 模型需易获得测量值.
首先, 根据获得的测量值对模型的过程参数进行实时更新, 即:
| ${{{y}}_k}[0,t]\xrightarrow{\rm {estimation}}{\hat x_k}[t]$ |
接着, 根据更新后的过程参数进行数值优化获得过程的最优点和操作轨迹, 即
| ${\hat x_k}[t]\xrightarrow{\rm {optimization}}{u^*}_k[t,{t_f}]$ |
最后, 重复上述步骤, 直至得到最优解.
该优化方法十分依赖过程模型, 如果过程模型的误差较大, 该方法的优化效果就会受到影响, 因此对过程模型的更新十分重要. 此外, 当输入接近最优值时, 该方法无法通过不断激励输入来克服未知参数的干扰.
(2) 不需要模型的实时隐性优化方法, 使用在线监测获得的测量值直接更新输入值. 代表性的方法有自优化控制[18]和NCO (Necessary Condition of Optimization)[19]. 自优化控制是通过批内变量的因果性, 对有干扰和不确定因素的系统进行优化. NCO是基于一个名义上的过程模型, 设计控制器跟踪优化目标的必要条件, 并通过数值优化获得NCO的结构信息, 再利用测量值强制过程与结构信息匹配[17]. NCO的算法步骤是:
首先, 根据目标函数优化所需条件, 建立有关NCO的模型, 即:
| ${y_k}[0,t]\xrightarrow{\rm {prediction}}{\rm{NCO}}$ |
然后, 根据必要条件求解最优解.
1.3 批次对比优化基于间歇生产过程的重复性, 研究人员设计出了批次对比优化算法, 通过迭代算法将上一批次获得的有价值的历史数据运用到当前批次中, 不断改进优化指标. 批次对比优化的关键就是如何在上个批次中获得有用的信息来优化接下来的批次.
批次对比优化算法可分为两类, 一类是基于模型的统计优化方法, 如主元分析(Principal Component Analysis, PCA)、最小二乘(Partial Least Squares, PLS)等多变量统计分析方法[20], 通过对检测得到的数据或变量进行系统分析, 得到必要的数据维数, 由此构造优化目标和过程变量之间的数学模型, 再根据该模型结合在线测量值更新操作轨迹. 算法步骤为:
首先, 根据监测得到的测量对目标参数进行实时更新, 即:
| ${y_k}[0,{t_f}]\xrightarrow{\rm {identification}}{\hat \theta _k}$ |
然后, 根据得到的过程参数, 进行数值计算, 再利用上一批次获得的数据进行对比优化, 得到下一批次的参数优化值, 即:
| ${\hat \theta _k}\xrightarrow{\rm {optimization}}{u^*}_{k + 1}[0,{t_f}]$ |
此优化方法的优点是能建立决策过程的经验化模型, 并可以实时观察过程的变化, 缺点是对含有扰动和不确定因素的过程, 其优化效果不佳, 使用范围比较局限, 无法扩展到其他过程优化中.
批次对比优化算法的另一类是使用趋势模型. 根据间歇生产过程的重复性, 利用积累的操作经验和过去生产的历史数据优化和改进现有的过程模型以及通过模型预测最优轨线的一种设想. 文献[21]采用趋势模型算法, 将其运用到状态估计器的设计上, 并使用该模型来改进扩展Kalman滤波器, 实现对间歇反应过程的实时优化. 该类优化方法不依赖精确的模型, 可以有效地处理间歇过程的不确定性, 算法步骤为:
首先, 基于优化目标的操作条件和约束来设计NCO, 即:
| ${y_k}[0,{t_f}]\xrightarrow{\rm {prediction}}{\rm{NCO}}$ |
然后, 根据必要条件及前一批次数据, 重复运行获得最优解.
需要说明的是, 实时优化和批次对比优化在有些时候是可以实现综合优化的[17]. 例如, 基于模型的优化, 可以利用实时优化来估计状态, 同时在过程运行时根据获得的数据来预测模型的参数. 在无模型的优化中, 利用实时优化来得到近似的更新率, 再在批次运行中设计终端约束和灵敏度预测的控制器.
近三十年来, 间歇生产过程优化方法成果斐然, 各有各的优势, 传统的离线优化研究的人已经很少了, 这里不做赘述, 仅对在线优化和批次对比优化方法进行总结, 它们的优、劣势及适用场景见表1.
| 表 1 间歇生产过程的优化方法分类 |
无论是在线优化还是批次对比优化, 都是对生产过程中的设定值的优化, 间歇生产过程中的过程参数(温度、流量或压力等)通常不是一个定值, 是通过对优化目标(产品质量指标、能量指标或效率指标)进行优化而得到的一条参数变化曲线. 优化目标与过程参数之间的关系往往十分复杂, 建立精确而又简易模型来描述两者关系十分困难, 如何在此情况下进行过程对象的优化是研究的重点. 近年来有很多研究者们利用在线优化和批次对比优化各自的优点, 将两种类型的优化方法结合起来, 综合这两种算法各自的优点, 形成混合优化方法. 文献[22]针对不确定条件下中间存储时间有限的多产品间歇生产过程调度问题, 通过模糊排序建立了数学模型, 将分布估计和粒子群优化结合, 设计出IPSO-EDA混合算法. 文献[23]针对化工过程优化问题, 将控制变量参数化方法(Control Variables Parameterization, CVP)和PSO相结合, 利用PSO对最优控制量进行求解, 控制变量参数化方法将获得的解作为初始给定轨迹, 进行二次优化. 相比于单层PSO算法, 该策略提高了算法的优化精度; 相比于单层CVP算法, 该策略提高了算法的优化效率.
2 间歇生产过程控制策略间歇生产过程的控制问题是在不违反操作条件和约束的情况下, 对最优控制轨迹的跟踪问题. 相比于连续生产过程, 间歇生产过程控制的难点主要有: (1)间歇生产过程没有稳定的工作点, 设定点和控制时间是不断变化的; (2)间歇生产过程具有非线性[24]; (3)对象模型一般存在不确定性, 且生产过程有不确定的干扰, 大多带有约束条件.
这些难点给间歇生产过程控制问题的研究带来了挑战, 同时间歇生产过程的重复性和慢速过程特性又为解决这些难点创造了机会.
传统的间歇生产过程控制是基于经典控制理论, 采用常见的仪器仪表, 对生产过程中的温度、流量、压力和液位进行控制[25,26], 根据不一样的控制目标和控制要求, 以单输出的比例-积分-微分控制策略为核心, 建立特定的操作模型, 文献[27]分别以化工过程常遇到的一阶、二阶和具有纯滞后的对象为例, 设计了克服干扰的前馈—反馈控制和串级控制, 并优化具有延迟特性的Smith预估补偿器. 传统控制策略的主要任务是稳定系统, 但对具有时变性和非线性, 且存在外界干扰的间歇生产过程, 传统控制策略无法满足控制要求. 为了实现更好的控制效果, 开始了智能控制和先进控制策略的研究.
2.1 智能控制策略智能控制是针对一类模型复杂而难以建立数学模型的生产过程的控制方法, 主要的控制方法有模糊控制和神经网络控制[28].
模糊控制是基于模糊推理和模仿人的思维方法,对难以建立精确的数学模型的对象实施的一种控制[29]. 它能够用模糊语言把过去研究人员总结的控制经验表示成特定的控制规则, 从而实现对系统的控制. 文献[30-32]针对间歇生产过程的非线性和时变性导致的模型难以建立的问题, 结合工程人员的丰富经验, 把模糊规则控制和传统控制策略融合, 制定综合操作计划, 获取了不错的应用价值.
模糊控制需要依靠操作人员的经验, 不具有通用性. 于是, 随着神经网络理论的深入研究, 神经网络控制接替模糊控制成为控制领域的研究重点, 引起了研究人员的研究兴趣. 对于间歇生产过程控制系统, 神经网络控制具有以下优势: (1)万能逼近特性, 可以无限接近最优操作轨迹. (2)自主优化能力强, 能够克服系统的时变性. (3)采用并行分布处理方法, 节省计算时间. (4)鲁棒性和容错性较强. (5)适用多变量系统. 充分利用这些优势, 对间歇系统和难以建模系统, 可以创造出新的控制思路. 文献[33-36]将神经网络应用到间歇过程的建模和控制中, 增加了模型的准确性, 改善了对过程的控制性能. 但仅靠一个神经网络控制无法避免局部极值及过度训练. 文献[37]针对原油蒸馏过程, 提出Bootstrap多神经网络的非线性软测量建模方法, 该方法比单一神经网络具有更高的准确率和鲁棒性.
智能控制策略虽然能在一定程度上实现良好的控制效果, 但仍有几点不足: (1) 当遇到含有复杂约束和不确定情况的间歇生产过程时, 由于无法了解过程的具体操作情况或者无法获取大量实验数据, 而难以建立过程模型, 对于这种情况, 该策略无法实现很好的控制效果. (2) 该策略的控制算法往往需要在线处理非线性优化问题, 使用数值求解的方法对于我们的计算能力是很大的考验.
2.2 先进控制策略先进控制策略是以现代控制理论为基础, 对较复杂的生产过程进行控制, 主要有自适应控制、鲁棒控制、预测控制和迭代学习控制[38].
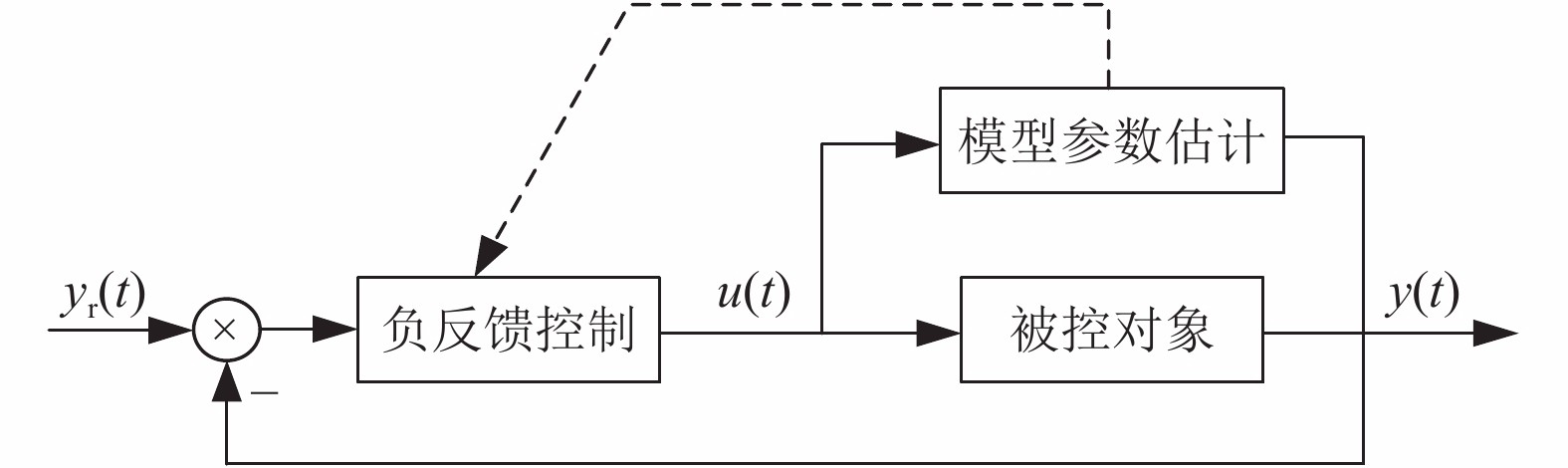
自适应控制是针对控制目标的特性不停变化和存在不可测因素的生产过程的控制策略. 该控制策略具有一定的适应能力, 执行器设定值随着过程参数的改变而不同, 以确保当控制对象特性变化时, 系统仍能达到控制要求. 文献[39]在注塑成型中使用自适应算法来控制注射速度, 通过在线测量得到的输入输出数据来估计出系统模型, 再通过模型配置闭环系统的零极点, 如图2所示. 在此基础上文献[40]用GPC控制器代替了零极点配置控制器, 有效的克服了控制器对模型失配敏感的问题.
|
图 2 自适应控制器示意图 |
比较经典反馈控制, 自适应控制确实提高了生产过程的实验结果. 但当批次更迭时或过程特性变化时, 自适应控制系统的输出会出现不稳定的现象, 需要一定时间进行调整, 导致控制效率的优势欠缺.
鲁棒控制可以消除间歇生产过程中因模型失配而产生的不良影响. 文献[41]以非线性系统的鲁棒镇定和鲁棒L2干扰抑制问题为主线, 概括介绍了基于耗散性的非线性过程鲁棒控制领域的新进展. 鲁棒控制常和自适应控制综合来实现生产过程的控制目标, 鲁棒控制器消除系统干扰和未建模动态的影响, 但当系统存在不确定参数时, 计算难度较大, 而自适应控制可以克服系统的不确定参数, 因此两者相结合能够产生比各自独立作用更好的控制效果. 文献[42-44]都是将自适应鲁棒控制应用到参数不确定的非线性系统, 验证了结合后的算法鲁棒性和准确性都更好. 文献[45]基于非线性船舶运动模型, 在考虑参数不确定的同时, 还加入了外界扰动, 提出了非线性Backstepping自适应鲁棒控制算法. 文献[46]将反馈控制与自适应鲁棒控制组合, 构成中药溶液糖析出系统的控制器, 验证了方法的有效性.
自适应控制和鲁棒控制能够克服生产过程中的数据无法测量引起的弊端, 确保生产的产品质量没有差异, 达到优化控制的目的. 但自适应控制和鲁棒控制只能用于过程参数在限制边界内不明显改变的状况, 其优化控制的范围是很有限的. 对于批次较多且频繁切换的生产过程, 模型预测控制和迭代学习控制更适合.
模型预测控制(Model Predictive Control, MPC)是面向实际运行结果与理论结果有偏差的生产过程, 对处理含约束和不确定因素干扰的多参数生产过程的控制问题上具有很大的潜能. 模型预测控制具有以下特点: 对模型的宽容性; 有限时域的滚动优化的有效性; 设计时考虑各种软、硬约束的可能性[47]. 基于这些特点, 很多学者将其应用到间歇生产过程控制系统. 针对间歇生产过程的特点, 研究较多的是多模型预测控制(Multiple Model Predictive Control, MMPC)和非线性模型预测控制(Nonlinear Model Predictive Control, NMPC)[13].
MMPC是针对一类非线性过程提出的一种预测控制策略, 其特点是将非线性过程以多时段线性模型或仿射线性模型近似并用作预测模型[48]. 把间歇生产过程的运行周期划分为一个个的小时间段, 再对这些小时间段的生产过程建立线性模型, 这些线性模型组合出整个间歇生产过程的近似模型. 文献[49]应用了基于线性不等式的鲁棒模型预测控制, 构造了MMA聚合的连续搅拌式反应釜的多元分布模型, 实现了对各种输入顺序的控制, 结果表明, 尽管模型具有不确定性, 该策略对反应器的特性的控制却很好, 且保证了系统的鲁棒性. 文献[50]针对污水生化处理过程, 首先从积累的过程输入输出数据中找出与当前过程状态一致的数据集合, 运用局部多项式拟合方法构造过程的局部模型, 再基于过程的变化建立数个模型, 将所得数个模型与MPC相融合, 得到MMPC方法.
NMPC是针对弱非线性过程的控制方法, 将整个过程划分为几段, 每段建立线性模型, 将非线性过程用多个线性模型组合来近似. 对于强非线性过程, 以线性模型作为MPC很难预测过程的动态行为, 而NMPC能很好的解决这一问题. NMPC问题一般通过离散化技术转化为非线性规划问题, 然后采用非线性规划求解器进行求解. 文献[51]采用多参数非线性预测控制模型, 在被控对象模型不匹配, 参数不确定及存在干扰的情况下, 进行控制模拟, 结果证明, 多速率NMPC的控制效果比线性多速率MPC和单速率MPC都要好. 文献[52]针对湿法冶金浸出过程, 分别采用线性化的MPC方法和基于全局正交配置法的NMPC方法, 从跟踪性能、抗扰性能和模型失配鲁棒性能3个方面进行了浸出率控制效果仿真对比, 证明了NMPC方法超调量小, 响应速度快, 稳定性高, 且在模型失配的情况下具有较强的鲁棒性.
迭代学习控制(Iterative Learning Control, ILC)是根据过去积累的控制经验和过程输出误差来优化当前的控制效果, 使被控系统的实际输出轨迹在有限时间区间内尽可能收敛于期望的输入轨迹[53], 通过学习降低控制算法对模型准确性的依赖. 文献[54]提出了基于模型的迭代学习控制, 利用先前批次的跟踪误差修正当前批次的系统输入, 降低了对模型准确性的依赖. 由于间歇生产过程需要在规定的时间里完成多个批次的生产任务, 所以通常从时间和批次两个维度来研究它的优化和控制问题. 基于间歇生产过程的二维表示, 文献[55-57]分别提出了4种类型的迭代学习控制算法, 提高了算法的收敛速度和鲁棒性. 以及文献[58]的利用多批次输入输出信息的高阶迭代学习控制算法. 这类算法利用大量的数据不断更新过程模型, 因此对模型的准确性要求不严格. 文献[59,60]针对间歇生产过程的模型不准确问题, 引入组合思想, 将控制条件与获得的历史数据进行综合寻优, 再结合迭代学习策略实现控制效果. 文献[61]根据最优轨迹的特性, 对输入轨线采取一定程度的参数化处理, 并结合迭代学习实现控制效果, 在实现了所需的控制效果的情况下, 简化了原本的迭代控制系统. 文献[62]针对空调在运行过程中会遇到各种不同的干扰问题, 提出了一种二维框架理论的迭代学习预测控制.
LC是利用历史数据来更新系统, 对生产过程将要出现的问题无法预测, 无法克服生产过程中的“临时干扰”. MPC是通过预测未来的系统状态输出, 进行滚动时域优化, 能及时处理实时干扰, 保证时域跟踪性能及闭环稳定性, 弥补了ILC的不足[63], 因此模型预测控制的迭代学习是控制间歇生产过程的一种重要方法. 文献[64-66]针对有约束的二维系统, 提出了一些基于模型预测控制的迭代学习控制方法.
综上所述, 间歇生产过程的控制技术飞速发展, 要在实际生产过程中实现好的控制效果, 需要使用合适的控制策略, 表2为各类控制策略的优、劣势以及使用场景的简单介绍. 对于批次数量非常有限, 或者生产过程耗时较长, 并且不同生产过程的控制模型的设定值差异很大的过程, 不宜用ILC和NMPC, 使用鲁棒控制和自适应控制的效果更佳.
| 表 2 间歇过程的控制策略分类 |
2.3 混合控制策略
混合控制是将传统控制、智能控制和先进控制的控制策略组合起来实现对间歇生产过程的控制. 文献[67]针对间歇生产过程存在的参数时变问题, 将在线自适应调节和ILC组合起来建立综合控制模型, 通过仿真验证, 该策略改善了间歇发酵过程的控制性能. 文献[68]针对初始状态不确定和存在干扰的系统, 将鲁棒控制和ILC一起应用到注塑机注射速度的控制中, 结果表明, 该算法的鲁棒性较强, 有效改善了系统的控制效果. 文献[69]通过最小二乘法辨识得到时变偏扰模型, 并进一步将迭代学习算法和S-procedure鲁棒方法相结合, 实验证明, 该设计对系统的收敛性更高, 达到了很好的控制效果.
当系统中存在不重复干扰时, 有人提出将迭代学习控制算法与批次内的反馈控制算法结合形成反馈迭代学习控制[70], 如图3所示. 文献[71]针对间歇过程反应器的模型误差和随机干扰问题, 在最优迭代学习控制的框架下引入时间反馈机制, 在生产过程的每个批次中, 不断利用当前信息校正过程中特性变化的过程输出. 文献[72]在文献[71]的基础上, 提出了一种两阶段(two-stage)的结合方式, 以降低算法对不重复干扰的敏感性.
由于间歇生产过程有时间和批次两个维度, 于是又提出用二维控制理论来分析设计反馈迭代学习控制方法. 文献[65]基于二维控制理论, 提出了一种间歇生产过程的集成预测迭代学习控制(2D-Integrated Predictive Iterative Learning Control, 2D-IPILC)策略. 文献[73]针对存在批次变化传感器故障的间歇过程, 基于间歇生产过程的容错控制, 引入迭代学习控制律, 建立了高阶控制模型, 证明了容错闭环系统的稳定性和鲁棒性.

|
图 3 反馈迭代学习控制示意图 |
总之, 针对间歇生产过程的控制技术的发展已经有了很大的突破, 各种控制策略也相对成熟. 但仍然存在待研究的问题, 比如对不确定时长的间歇生产过程的控制问题, 以及如何利用得到的数据对时变系统建立精确的模型问题, 以更好的提高算法的收敛性能和控制效果.
3 结论与展望针对间歇生产过程的“多重时变”特性, 本文分别综述了近年来的优化方法和控制策略. 对于间歇生产过程的优化方法, 主要从基于测量值的在线优化和基于模型的批次对比优化两个方面进行陈述. 从本文的分析可以看到, 在线优化和批次对比优化均是间歇生产过程的研究热点, 研究成果也十分斐然, 但间歇过程的优化方法仍在发展过程, 未来的研究前景:
(1)现在间歇生产过程的优化方法大部分都需要系统模型, 而现实工厂运行中构造精确的系统模型具有很大的挑战, 缺乏精确的过程模型、生产过程存在干扰和不确定因素,, 如何常采用合适的组合优化方法, 解决这些问题的同时, 系统的稳定性不受到影响. 例如, 对于间歇生产过程难以建立精确的数学模型问题, 前面有提到一种无模型优化方法, 但这种方法通常需要大量的实现数据, 如何结合其他优化方法从而实现扬长避短还需要大家来研究.
(2)当间歇生产过程的过程特性发生变化时, 过程的控制参数需要随之变化. 例如, 在乙酸乙酯的生产过程中, 当催化剂或反应原料发生变化时, 为了获得合格的乙酸乙酯产品, 需要更改进料流率、釜温和釜内压强等过程参数. 因此我们要获取优化目标和过程参数之间的数学关系, 这就需要基于大量的实验数据来建立生产过程的模型. 还有一些间歇生产过程因为产品发生变化而改变了过程特性, 这时可以利用前个产品的实验数据来对新的产品建模. 目前已经有人提出了基于过程相似特性的模型移植策略, 不过这方面的理论研究和应用还不够成熟, 还需要进一步对如何界定产品的相似性和如何甄别有用的数据来研究.
对于间歇生产过程的控制策略, 主要从3种控制策略方面进行叙述. 虽然近三十年, 间歇生产过程的控制策略研究取得了不少成果, 但仍存在很多问题需要改进:
(1)对于基于模型的控制策略来说, 精确模型对于获得好的控制效果至关重要. 迭代学习的引入一定程度上降低了控制策略对模型的依赖, 但精确的模型仍能提供更好的控制效果和控制速率. 对于间歇生产过程来说, 建模的难点在于过程的时变性, 而如何利用过程的重复性对时变性的过程进行建模仍需要研究.
(2) 间歇生产过程大多具有很明显的非线性, 为了降低在线计算的复杂度, 前一节提到的基于迭代学习的控制策略的原理是将非线性过程划分为多个线性过程, 建立线性模型以近似非线性过程. 如文献[74]在不同的时间点, 将非线性模型进行线性处理, 通过对非线性过程进行划分, 获得多个线性模型, 用这些线性模型来近似为非线性过程. 针对这些线性模型完成非线性过程的控制策略的设计. 当间歇生产过程的非线性较弱, 且没有复杂的约束和不确定因素的干扰时, 这种近似化方法是可行的. 但当过程的非线性无法得到高精度的近似时, 这种方法获得的控制策略无法具有说服力, 需要更加合适的控制策略来解决, 这值得大家去研究.
间歇生产过程的优化方法和控制策略的研究仍落后于连续生产过程, 对间歇生产过程的研究还不够, 而传统的连续生产过程的优化方法和控制策略不宜用于间歇生产过程, 此外, 还需要加强改进算法和现代控制理论的融合, 研究出适合大多数的间歇生产过程的控制与优化软件且实现产业化具有必要性.
| [1] |
丁进良, 杨翠娥, 陈远东, 等. 复杂工业过程智能优化决策系统的现状与展望. 自动化学报, 2018, 44(11): 1931-1943. |
| [2] |
Hawkins WM, Fisher T. Batch control systems: Design, application, and implementation. Research Triangle Park, NC, USA: ISA, 2006.
|
| [3] |
卢静宜, 曹志兴, 高福荣. 批次过程控制—回顾与展望. 自动化学报, 2017, 43(6): 933-943. |
| [4] |
Nagy ZK, Braatz RD. Open-loop and closed-loop robust optimal control of batch processes using distributional and worst-case analysis. Journal of Process Control, 2004, 14(4): 411-422. DOI:10.1016/j.jprocont.2003.07.004 |
| [5] |
Lee J, Ramirez WF. Optimal fed-batch control of induced foreign protein production by recombinant bacteria. AIChE Journal, 1994, 40(5): 899-907. DOI:10.1002/aic.690400516 |
| [6] |
Srinivasan B, Bonvin D, Visser E, et al. Dynamic optimization of batch processes: II. Role of measurements in handling uncertainty. Computers & Chemical Engineering, 2003, 27(1): 27-44. |
| [7] |
陆鹏程. 间歇生产过程经济模型预测控制理论与应用[博士学位论文]. 杭州: 浙江大学, 2019.
|
| [8] |
许向阳, 于玲, 祝和云, 等. 间歇蒸煮过程计算机优化控制系统. 中国造纸学报, 2000, 15(1): 98-102. DOI:10.3321/j.issn:1000-6842.2000.01.020 |
| [9] |
竺建敏, 邵惠鹤, 蒋慰孙. 甲醛生产过程的数学模型与优化. 华东化工学院报, 1986, 12(S1): 1-11. |
| [10] |
Tian Y, Zhang J, Morris J. Optimal control of a batch emulsion copolymerisation reactor based on recurrent neural network models. Chemical Engineering and Processing: Process Intensification, 2002, 41(6): 531-538. DOI:10.1016/S0255-2701(01)00173-8 |
| [11] |
李春富, 叶昊, 王桂增. 基于多向PLS方法的间歇过程质量预测. 系统仿真学报, 2004, 16(6): 1168-1170, 1174. DOI:10.3969/j.issn.1004-731X.2004.06.016 |
| [12] |
李春富. 基于数据的软测量建模方法及其应用的研究[博士学位论文]. 北京: 清华大学, 2005.
|
| [13] |
陈治纲, 许超, 邵惠鹤. 间歇过程优化与先进控制综述. 化工自动化及仪表, 2003, 30(3): 1-6. DOI:10.3969/j.issn.1000-3932.2003.03.001 |
| [14] |
张亚如, 陈志凤, 蔡秀峰. 基于自适应律的RBF磨矿分级优化控制过程. 数字技术与应用, 2019, 37(8): 1-2. |
| [15] |
Rahman AKMS, Palanki S. On-line optimization of batch processes with nonlinear manipulated input. Chemical Engineering Science, 1996, 51(3): 449-459. DOI:10.1016/0009-2509(95)00268-5 |
| [16] |
Gattu G, Zafiriou E. A methodology for on-line setpoint modification for batch reactor control in the presence of modeling error. Chemical Engineering Journal, 1999, 75(1): 21-29. DOI:10.1016/S1385-8947(99)00074-1 |
| [17] |
史洪岩, 苑明哲, 王天然, 等. 间歇过程动态优化方法综述. 信息与控制, 2012, 41(1): 75-82. |
| [18] |
Skogestad S. Plantwide control: The search for the self-optimizing control structure. Journal of Process Control, 2000, 10(5): 487-507. |
| [19] |
Welz C, Srinivasan B, Bonvin D. Measurement-based optimization of batch processes: Meeting terminal constraints on-line via trajectory following. Journal of Process Control, 2008, 18(3–4): 375-382. |
| [20] |
Srinivasan B, Primus CJ, Bonvin D, et al. Run-to-run optimization via control of generalized constraints. Control Engineering Practice, 2001, 9(8): 911-919. DOI:10.1016/S0967-0661(01)00051-X |
| [21] |
Fotopoulos J, Georgakis C, Stenger Jr HG. Use of tendency models and their uncertainty in the design of state estimators for batch reactors. Chemical Engineering and Processing: Process Intensification, 1998, 37(6): 545-558. DOI:10.1016/S0255-2701(98)00061-0 |
| [22] |
耿佳灿, 顾幸生. 不确定条件下中间存储时间有限多产品间歇生产过程调度. 化工学报, 2015, 66(1): 357-365. |
| [23] |
石博文, 尹燕燕, 刘飞. 基于PSO-控制变量参数化混合策略的间歇化工过程优化控制. 化工学报, 2019, 70(3): 979-986. |
| [24] |
冯健. 清漆生产集散控制系统的设计与仿真[硕士学位论文]. 沈阳: 东北大学, 2012
|
| [25] |
邹志云, 桂新军. 间歇化工过程先进控制技术的应用与发展评述. 石油化工自动化, 2009, 45(1): 1-6. DOI:10.3969/j.issn.1007-7324.2009.01.001 |
| [26] |
向阳. 基于CAN总线的一体化测控单元的研究[硕士学位论文]. 广州: 广东工业大学, 2005.
|
| [27] |
邵惠鹤. 比例、积分、微分和前馈调节规律的最优性. 化工自动化及仪表, 1983(2): 16-21. |
| [28] |
李力争. 凿岩机器人双三角钻臂自适应控制策略研究[博士学位论文]. 长沙: 中南大学, 2003.
|
| [29] |
李文, 欧青立, 沈洪远, 等. 智能控制及其应用综述. 重庆邮电学院学报(自然科学版), 2006, 18(3): 376-381. |
| [30] |
李永彪, 孙正贵, 赵清杰. 间歇聚丙烯生产的智能控制方案. 工业仪表与自动化装置, 2002(5): 15-17, 25. DOI:10.3969/j.issn.1000-0682.2002.05.004 |
| [31] |
邸书玉. 间歇液相本体法聚丙烯全过程控制系统研究与应用[硕士学位论文]. 长春: 长春理工大学, 2006.
|
| [32] |
张祖鹰. 间歇生产过程的复合模糊PID控制. 制造业自动化, 2010, 32(15): 39-41, 47. |
| [33] |
Bhat N, McAvoy TJ. Use of neural nets for dynamic modeling and control of chemical process systems. Computers & Chemical Engineering, 1990, 14(4–5): 573-582. |
| [34] |
Zhang J. Developing robust neural network models by using both dynamic and static process operating data. Industrial & Engineering Chemistry Research, 2001, 40(1): 234-241. |
| [35] |
Hunt KJ, Sbarbaro D, Żbikowski R, et al. Neural networks for control systems–A survey. Automatica, 1992, 28(6): 1083-1112. |
| [36] |
Zhang J, Morris AJ. Nonlinear process modelling using dynamic neuro-fuzzy networks. IFAC Proceedings Volumes, 1997, 30(9): 353-358. DOI:10.1016/S1474-6670(17)43181-8 |
| [37] |
周长, 张杰, 吕文祥, 等. 基于Bootstrap多神经网络的软测量方法. 控制工程, 2009, 16(4): 475-477, 506. DOI:10.3969/j.issn.1671-7848.2009.04.027 |
| [38] |
陈雷. 基于软测量技术的C5石油树脂粘度的在线检测研究[硕士学位论文]. 上海: 上海交通大学, 2009.
|
| [39] |
Yang Y, Gao FR. Injection velocity control using a self-tuning adaptive controller. International Polymer Processing, 1999, 14(2): 196-204. DOI:10.3139/217.1537 |
| [40] |
Yang Y, Gao FR. Adaptive control of the filling velocity of thermoplastics injection molding. Control Engineering Practice, 2000, 8(11): 1285-1296. DOI:10.1016/S0967-0661(00)00060-5 |
| [41] |
慕春棣, 梅生伟, 申铁龙. 非线性系统鲁棒控制理论的一些新进展. 控制理论与应用, 2001, 18(1): 1-6. DOI:10.3969/j.issn.1000-8152.2001.01.001 |
| [42] |
Haddad WM, Hayakawa T, Chellaboina VS. Robust adaptive control for nonlinear uncertain systems. Automatica, 2003, 39(3): 551-556. DOI:10.1016/S0005-1098(02)00244-3 |
| [43] |
Xu HJ, Ioannou PA. Robust adaptive control of linearizable nonlinear single input systems with guaranteed error bounds. Automatica, 2004, 40(11): 1905-1911. DOI:10.1016/j.automatica.2004.04.019 |
| [44] |
Qu ZH. Adaptive and robust controls of uncertain systems with nonlinear parameterization. IEEE Transactions on Automatic Control, 2003, 48(10): 1817-1824. DOI:10.1109/TAC.2003.817931 |
| [45] |
叶宝玉, 王钦若, 熊建斌, 等. 船舶航向非线性backstepping自适应鲁棒控制. 控制工程, 2013, 20(4): 607-610. DOI:10.3969/j.issn.1671-7848.2013.04.005 |
| [46] |
段洪君, 梁家琦, 孙佳亨, 等. 中药糖析出自适应鲁棒控制. 控制工程, 2019, 26(12): 2176-2180. |
| [47] |
席裕庚, 耿晓军, 陈虹. 预测控制性能研究的新进展. 控制理论与应用, 2000, 17(4): 469-475. DOI:10.3969/j.issn.1000-8152.2000.04.001 |
| [48] |
Camacho EF, Bordons C. Model predictive control. London: Springer-Verlag, 1999.
|
| [49] |
Park MJ, Rhee HK. LMI-based robust model predictive control for a continuous MMA polymerization reactor. Computers & Chemical Engineering, 2001, 25(11–12): 1513-1520. |
| [50] |
曾静, 薛定宇, 袁德成. 非线性系统的多模型预测控制方法. 东北大学学报(自然科学版), 2009, 30(1): 26-29. DOI:10.3321/j.issn:1005-3026.2009.01.007 |
| [51] |
Prasad V, Schley M, Russo LP, et al. Product property and production rate control of styrene polymerization. Journal of Process Control, 2002, 12(3): 353-372. DOI:10.1016/S0959-1524(01)00044-0 |
| [52] |
白璐. 湿法冶金浸出过程非线性预测控制方法的研究[硕士学位论文]. 沈阳: 东北大学, 2017.
|
| [53] |
邹志云, 刘燕军, 刘兴红, 等. 精细化工过程控制技术的重要发展趋势. 冶金自动化, 2011, 35(5): 11-16. |
| [54] |
Lee JH, Lee KS. Iterative learning control applied to batch processes: An overview. Control Engineering Practice, 2007, 15(10): 1306-1318. |
| [55] |
Wang DW. On D-type and P-type ILC designs and anticipatory approach. International Journal of Control, 2000, 73(10): 890-901. DOI:10.1080/002071700405879 |
| [56] |
Park KH. A study on the robustness of a PID-type iterative learning controller against initial state error. International Journal of Systems Science, 1999, 30(1): 49-59. DOI:10.1080/002077299292669 |
| [57] |
池荣虎, 韩吉志, 刘宇. 间歇过程温度反应器的PD型迭代学习控制方法. 第三十四届中国控制会议论文集(B卷). 杭州, 中国. 2015.5.
|
| [58] |
Chen YQ, Gong ZM, Wen CY. Analysis of a high-order iterative learning control algorithm for uncertain nonlinear systems with state delays. Automatica, 1998, 34(3): 345-353. DOI:10.1016/S0005-1098(97)00196-9 |
| [59] |
Xiong ZH, Zhang J. Product quality trajectory tracking in batch processes using iterative learning control based on time-varying perturbation models. Industrial & Engineering Chemistry Research, 2003, 42(26): 6802-6814. |
| [60] |
Xiong ZH, Zhang J, Dong J. Optimal iterative learning control for batch processes based on linear time-varying perturbation model. Chinese Journal of Chemical Engineering, 2008, 16(2): 235-240. |
| [61] |
叶凌箭, 马修水, 宋执环. 基于输入轨迹参数化的间歇过程迭代学习控制. 化工学报, 2016, 67(3): 743-750. |
| [62] |
周勇. 柔性迭代学习控制的高精度空调智能控制策略. 信息技术, 2020, 44(2): 83-88. |
| [63] |
马乐乐, 刘向杰. 变参考轨迹下的鲁棒迭代学习模型预测控制. 自动化学报, 2019, 45(10): 1933-1945. |
| [64] |
Wang LP, Freeman CT, Chai S, et al. Predictive-repetitive control with constraints: From design to implementation. Journal of Process Control, 2013, 23(7): 956-967. DOI:10.1016/j.jprocont.2013.03.012 |
| [65] |
Chen C, Xiong ZH, Zhong YS. Design and analysis of integrated predictive iterative learning control for batch process based on two-dimensional system theory. Chinese Journal of Chemical Engineering, 2014, 22(7): 762-768. DOI:10.1016/j.cjche.2014.05.008 |
| [66] |
Jin ST, Hou ZS, Chi RH. A novel data-driven terminal iterative learning control with iteration prediction algorithm for a class of discrete-time nonlinear systems. Journal of Applied Mathematics, 2014, 2014: 307809. DOI:10.1155/2014/307809 |
| [67] |
王志文. 间歇过程2D-PID自适应迭代学习控制研究[硕士学位论文]. 杭州: 浙江工业大学, 2016.
|
| [68] |
崔彩莲. 迭代学习控制的频域设计及在注塑机上的应用[硕士学位论文]. 浙江: 浙江工业大学, 2006.
|
| [69] |
孙海乔, 陈珺, 刘飞. 二次型鲁棒迭代学习控制在间歇过程中的应用. 计算机与应用化学, 2013, 30(10): 1148-1152. DOI:10.3969/j.issn.1001-4160.2013.10.014 |
| [70] |
Lee KS, Bang SH, Chang KS. Feedback-assisted iterative learning control based on an inverse process model. Journal of Process Control, 1994, 4(2): 77-89. |
| [71] |
Jang JSR, Sun CT. Neuro-fuzzy modeling and control. Proceedings of the IEEE, 1995, 83(3): 378−406. |
| [72] |
Chin I, Qin SJ, Lee KS, et al. A two-stage iterative learning control technique combined with real-time feedback for independent disturbance rejection. Automatica, 2004, 40(11): 1913-1922. DOI:10.1016/j.automatica.2004.05.011 |
| [73] |
张刘军, 索寒生, 彭秀莹. 带批变故障的间歇过程高阶学习容错控制. 控制工程, 2020, 27(6): 1055-1061. |
| [74] |
Liu T, Wang YQ. A synthetic approach for robust constrained iterative learning control of piecewise affine batch processes. Automatica, 2012, 48(11): 2762-2775. DOI:10.1016/j.automatica.2012.08.026 |
 2021, Vol. 30
2021, Vol. 30



