近年来, 基于户外环境获取步态数据构建泛化性能优越的机器学习步态分类模型在步态模式识别研究领域受到广泛关注, 对于预防老年人跌倒、老年神经性功能疾病诊疗和康复评价、人体身份鉴别等具有重要意义, 已成为目前步态模式识别相关研究领域一个新的研究探索热点^[1,2]. 近年来, 随着先进数据采集技术快速发展, 一些先进的数据采集技术(诸如, 计算机视频、无线雷达、可穿戴传感器等)相继被用来采集户外环境中步态模式数据. 诸如, 一些学者基于计算机视频采集的步态图像数据, 探讨了不同视角环境下的户外人体步态模式识别相关研究^[3]; 另外一些研究学者基于无线雷达装置获取的步态数据, 探讨了蕴含微多普勒特征信息的户外环境步态模式识别研究^[4]; 还有一些学者基于可穿戴传感器(加速度计、陀螺仪、磁力计等)的步态数据, 探讨了户外环境下的步态模式识别研究^[5]. 研究发现, 便宜、便携的可穿戴传感器步态采集技术具有适应不同户外应用场景、蕴含较丰富步态特征信息量等优点, 可较好避免计算机视频技术因户外环境、人体穿戴衣物遮挡丢失有价值步态特征信息、无线雷达装置因外界环境干扰丢失无线步态探测信号等局限, 有助于提升步态模式识别效能, 在近年来相关研究应用较为广泛.

基于可穿戴传感器数据应用机器学习算法探寻泛化性能优越的步态模式识别模型受到相关研究持续高度关注, 其基本思想: 能够充分利用机器学习算法优越的数据学习性能从可穿戴传感器步态数据中获得更具代表性的步态特征信息, 提高步态模式识别性能. 早期, 一些研究探讨了基于传统机器学习算法(诸如, 决策树、多层感知神经网络、支持向量机、K-近邻等)量化分析可穿戴传感器数据, 尝试构建泛化性能优越的步态模式识别性能^[6,7]. 诸如, Bao等^[8]探讨了基于三轴加速度计步态数据, 构建ID3决策树步态模式识别模型鉴别正常行走、慢跑、爬楼梯等3种步态模式, 平均识别率仅为79%. Tahafchi等探讨了应用KNN分类算法从帕金森受试者可穿戴传感数据(包含三轴加速度数据、陀螺仪数据、磁力计数据以及双通道的非侵入型的肌电扫描仪数据)中获取与帕金森冻结步态密切相关的步态特征信息, 步态模式识别率根据参与者对象分别达到91.9%、87.1%、80.9%以及79.9%^[9]; 此外, Nickel等学者基于可穿戴传感器加速度步态数据, 分别探讨了基于支持向量机、隐形马尔可夫模型、KNN分类算法构建步态模式识别模型相关研究, 其中支持向量机以及隐形马尔可夫模型的平均错误率(Equal Error Rate, EER)分别是10.00%和12.63%, KNN分类算法的一半总错误率(Half Total Error Rate, HTER)可达到8.24%^[10,11]; 研究发现, 传统机器学习算法在处理可穿戴传感器步态数据识别步态模式中具有较低计算复杂度等优点, 但因其内在线性计算模型架构难以获取隐含于可穿戴传感器步态数据内在结构中更具代表性的步态特征信息, 难以支撑构建泛化性能优越的步态模式识别模型. 近年来, 随着深度学习等新兴机器学习理论的快速发展以及在图像处理等领域成功应用, 一些学者尝试探讨基于可穿戴传感器步态数据构建深度学习步态模式识别模型, 其基本思路旨在充分利用深度学习算法卓越的数据学习性能从高维可穿戴传感步态数据中获取更具代表性步态特征信息, 提高步态模式识别性能. 诸如, Zou等^[12]基于可穿戴智能手机采集的加速度数据和陀螺仪数据, 探讨了构建卷积神经网络和循环神经网络相融合步态模式识别模型, 尝试获取可穿戴传感步态数据内在时空相关性特征信息, 提高步态模式识别性能, 研究结果发现该方法在行人识别和身份认证中准确率分别高于93.5%和93.7%. 此外, Ding等^[13]研究学者提出了一种基于可穿戴步态数据(在小腿上佩戴惯性测量单元收集角速度数据)的长短时记忆算法LSTM的步态模式识别模型, 旨在通过长短时记忆算法获取隐含于可穿戴步态数据的时间相关性步态特征信息探测步态相位, 并利用相位标记数据对其进行训练, 实验结果表明识别准确率可达91.4%. 近年来的基于深度学习的步态模式识别相关研究虽取得了较好的成果和积极进展, 但仍缺乏准确获取隐含于可穿戴步态数据中更具代表性的时-空相关性步态特征信息的技术手段, 严重制约着步态模式识别性能. 相关医学研究表明, 步态是人体行走的姿态, 与人体神经系统、运动系统、心理认知系统等生理因素密切相关, 是一个各生理因素相互作用、相互影响的长期记忆过程, 而目前研究所采用自循环神经网络模型仅具短时记忆性能, 难以获得步态过程中长期时间相关性特征信息. 急需探索新的获取隐含于可穿戴步态数据中更具代表性的时-空相关性步态特征信息的深度学习模型.

为此, 基于可穿戴传感器步态数据, 本文提出一种将卷积神经网络模型和长短期记忆神经网络模型相融合的步态模式深度学习判别新模型, 旨在充分利用卷积神经网络模型优越的获取数据局部空间最具代表性特征信息特性和长短期记忆神经网络模型优越的获取数据内在长期时间相关性特征信息特性, 准确获取隐含于可穿戴步态数据中更具代表性的时-空相关性步态特征信息, 提高步态模式识别性能. 此外, 本文选取公开的加州大学欧文分校UCI数据库中的HAR数据^[14], 并与传统机器学习算法、深度学习算法模型比较, 验证本文所提模型算法有效性.

1 CNN-LSTM深度融合学习步态模式判别模型

本文所提CNN-LSTM深度融合学习模型旨在充分利用CNN、LSTM模型分别获取数据结构内在空间、时间相关性特征信息的优异特性, 将二者深度融合从可穿戴传感步态数据(诸如, 加速度、陀螺仪等步态数据)获取更多蕴含与步态变化密切相关的时-空相关性特征信息, 提高步态模式识别性能. 也就是, 假设需识别步态模式为数据集 $V = \left\{ {{v_1},{v_2}, \cdot \cdot \cdot ,{v_l}} \right\}$ , 其中, l表示待识别的步态模式数. 假设可穿戴传感步态时间序列数据为:

$D = \left( {{d^1}, \cdots ,{d^j}, \cdots ,{d^t}} \right) = \left( \begin{gathered} d_1^1, \cdots ,d_1^t \\ \vdots \\ d_m^1, \cdots ,d_m^t \\ \end{gathered} \right)$

(1)

其中, ${d^j} = {\left( {d_1^j, \cdots ,d_m^j} \right)^{\rm{T}}}$ 表示为在j时间点可穿戴传感数据, m和t分别表示可穿戴传感器数目和步态模式时间序列样本数目. 研究中, 将每一个步态模式 ${v_i}$ 时间序列数据进行数据段选取, 使每一数据段 ${h_i} = \left( {{t_{i - 1}},{t_i}} \right)$ 蕴含步态时空特征信息, 所有选取数据段定义为数据集 $H = \left\{ {{h_1}, \cdots,{h_i}, \cdots,{h_k}} \right\}$ , k为所有选取数据段数目.

为了准确识别步态模式, 我们需构建一个模型Γ从每一数据段 ${h_i}$ 中获取蕴含步态特征信息的向量Y_i, 也就是, ${Y_i} = \Gamma \left( {D,{h_i}} \right)$ 然后, 基于一个推理方法Ψ计算与每个步态模式 ${v_i}$ 相对应的置信度值集 $P:P\left( {{v_i}/{Y_i},\beta } \right) = \Psi \left( {{Y_i},\beta } \right)$ , 其中, $\;\beta $ 表示为一个基于模型Γ的训练参数集. 那么, 通过计算下列最大得分值: $v_i^ * = \arg \max P\left( {v/{Y_i},\beta } \right)$ , 即可准确获得步态模式 $v_i^ * $ , 实现每个步态模式 ${v_i}$ 识别. 研究中, 我们构建CNN-LSTM深度融合学习模型作为模型 $\Gamma $ , 首先采用CNN深度学习模型从每一数据段 ${h_i}$ 中获取蕴含与步态模式变化密切相关的局部空间特征信息, 在此基础上, 基于LSTM深度学习模型获取步态数据局部空间特征的时间相关性, 获得更多与步态模式变化相关的时-空特征信息, 最大概率获得到步态模式 $v_i^ * $ , 准确识别步态模式 ${v_i}$ .

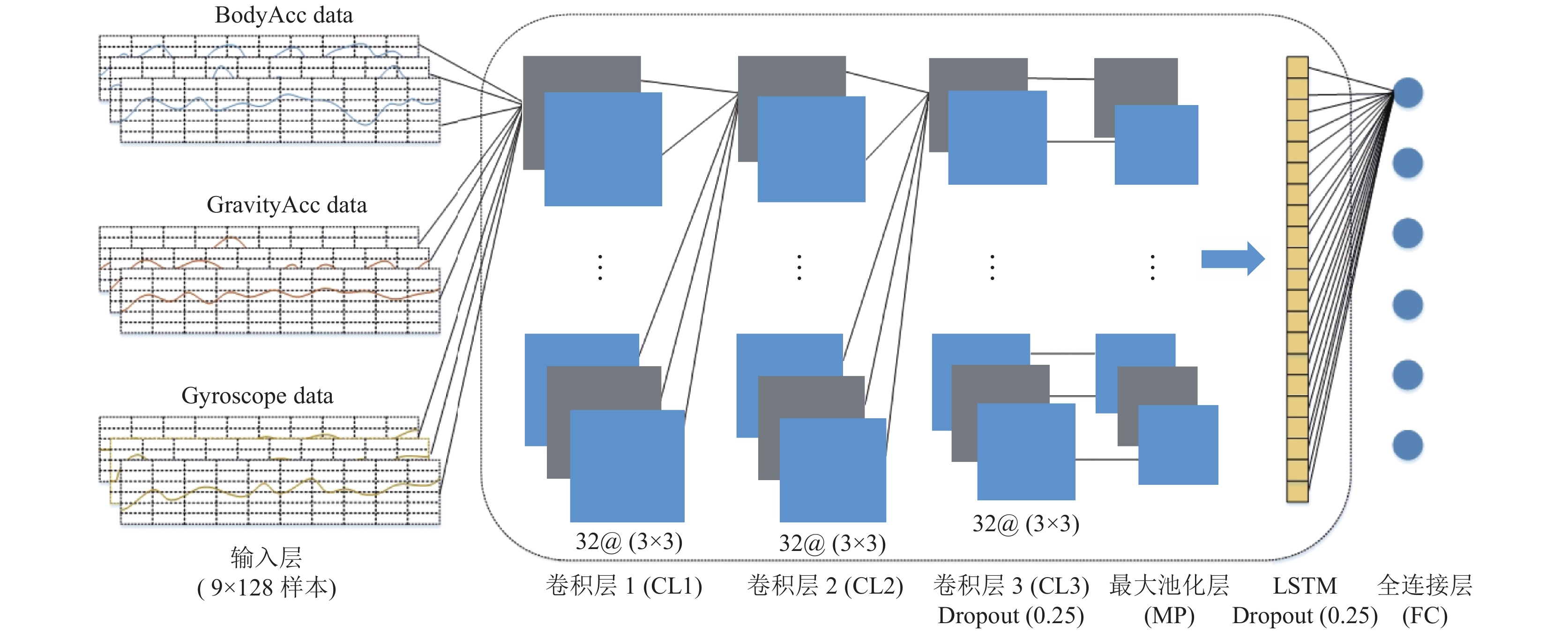
本文所提基于CNN-LSTM融合深度学习步态模式判别模型框架如图1所示, 由步态数据输入层、CNN-LSTM融合深度学习、全连接层3部分组成.

如图1, 鉴于可穿戴步态传感数据的时-空相关特性, CNN由3个卷积层(CL1、CL2、CL3), 一个池化层(MP1), 两个dropout层组成, 准确获取步态数据内在最具代表性的局部空间特征; 为准确获得步态数据内在最具代表性局部空间特征的时间相关性, LSTM模型由32个cell组成, 为准确获得步态数据内在最具代表性局部空间特征的时间相关性, 全连接层由6个cell组成, 最大概率识别步态模式.

(1)基于CNN提取步态数据内在最具代表性局部空间特征

为有效获取步态特征信息, 可穿戴传感步态时间序列在t时刻的数据定义为:

$\begin{split} {d^t} =& \left( {d_{BA\_x}^td_{BA\_y}^td_{BA\_{\textit{z}}}^td_{GA\_x}^td_{GA\_y}^t, } \right.\\ &\left. { d_{GA\_{\textit{z}}}^t,d_{Gy\_x}^t,d_{Gy\_{y}}^t,d_{Gy\_{\textit{z}}}^t} \right) \end{split} $

(2)

其中, BA-XYZ表示三维人体运动加速度数据, GA-XYZ表示三维重力加速度数据, Gy-XYZ表示三轴陀螺仪数据. 便于分析, 选取 $t \in \left\{ {1, \cdot \cdot \cdot ,128} \right\}$ , 其传感步态数据输入序列定义为:

$D = \left( {{d^1}, \cdot \cdot \cdot ,{d^t}, \cdot \cdot \cdot ,{d^{128}}} \right) = \left( \begin{gathered} d_{BA\_x}^1, \cdot \cdot \cdot ,d_{BA\_x}^{128} \\ d_{BA\_y}^1, \cdot \cdot \cdot ,d_{BA\_y}^{128} \\ d_{BA\_{\textit{z}}}^1, \cdot \cdot \cdot ,d_{BA\_{\textit{z}}}^{128} \\ d_{GA\_x}^1, \cdot \cdot \cdot ,d_{GA\_x}^{128} \\ d_{GA\_y}^1, \cdot \cdot \cdot ,d_{GA\_y}^{128} \\ d_{GA\_{\textit{z}}}^1, \cdot \cdot \cdot ,d_{GA\_{\textit{z}}}^{128} \\ d_{Gy\_x}^1, \cdot \cdot \cdot ,d_{Gy\_x}^{128} \\ d_{Gy\_y}^1, \cdot \cdot \cdot ,d_{Gy\_y}^{128} \\ d_{Gy\_{\textit{z}}}^1, \cdot \cdot \cdot ,d_{Gy\_{\textit{z}}}^{128} \\ \end{gathered} \right)$

(3)

假设用于获取最具代表性步态局部空间特征的CNN模型共有 $L$ 卷积层, 每层卷积核定义为: ${M_l} \times {N_l}$ , 第 $l \in \left\{ {1, \cdot \cdot \cdot ,L} \right\}$ 卷积层提取步态局部空间特征 ${F^{\left( l \right)}}$ , 其定义为:

$ {F^{\left( l \right)}} = f\left( {{b^{\left( l \right)}} + \left\langle {{w^{\left( l \right)}},{d^i}, \cdots ,{d^{i + \phi - 1}}} \right\rangle } \right), i = 1, \cdots ,t - \phi + 1 $

(4)

其中, $f( \cdot )$ 表示激活函数, $\left\langle \cdot \right\rangle $ 表示内积, ${b^{\left( l \right)}}$ 为偏置项; ${w^{\left( l \right)}}$ 为一维卷积核向量; $\phi $ 为 ${w^{\left( l \right)}}$ 的长度.

鉴于式(3)所定义的可穿戴传感步态数据所具高维性、非线性、随机性等特点和低算法复杂度, 本文构建三层一维卷积层, 每个卷积层均有32个卷积核, 其大小定义为3×3, 步长定义为1, 采用良好非线性特性ReLU函数^[15,16]作为激活函数. 根据式(3), 可穿戴传感步态输入数据大小定义为128×9, 可分别获得第一层、第二层以及第三层卷积层输出的步态局部特征数据: 126×32、124×32和122×32. 为有效保持较好学习性能避免过拟合, 构建一个Dropout层. 为有效保持卷积层所获得步态特征内在特性, 降低其冗余性信息, 利用池化层降低特征维数且增加其空间不变性^[17], 定义最大池化技术的池化层获取蕴含更多最具步态变化信息的局部空间特征 ${P_j}$ , 定义为:

$ {P_j} =\max \left( {{F_{\left( {j - 1} \right)R + 1}}, \cdots ,{F_{jR}}} \right), j = 1, \cdots ,t/R $

(5)

其中, R表示池化窗口大小.

为此, 基于式(5)可从可穿戴传感步态时间序列数据中得到最具步态变化信息的局部空间特征, 为后续获取其时间相关性特征奠定基础. 我们将此局部步态特征作为LSTM的输入提取步态数据长时期的依赖特性.

(2)基于LSTM层提取步态数据局部特征的时间相关性

一个步态活动可考虑为一个长序列的时间序列, 通过建立自回归模型RNN可有效提取局部特征的长期时间相关依赖特性. 本文鉴于长短期记忆网络(LSTM)所具良好动态学习时间序列数据内在时间相关性的自回归网络架构特性^[18], 构建LSTM单元cell, 包括1个记忆单元C和3个门函数(输入 ${i_t}$ , 遗忘 ${f_t}$ , 输出 ${o_t}$ ), 实时提取步态数据的内在长期时间相关特性信息, 具体实现如下.

假设用 ${p^t}$ 表示步态数据样本在t时刻通过CNN模型处理过的一维特征图作为LSTM神经元的输入项, 经过LSTM的cell时首先由遗忘门丢弃无用的提取数据信息, 其输出为:

${f_t} = \sigma \left( {{W_f} \cdot \left[ {{p^t},{h_{t - 1}}} \right] + {b_f}} \right)$

(6)

其中, σ表示激活函数Sigmoid, ${W_f}$ 为权值, ${b_f}$ 表示偏置值. 接着由输入门 ${i_t}$ 和候选记忆单元 ${\tilde C_t}$ 来确定更新的数据信息:

${i_t} = \sigma \left( {{W_i} \cdot \left[ {{p^t},{h_{t - 1}}} \right] + {b_i}} \right)$

(7)

$\tilde C = \tan ({W_c} \cdot \left[ {{p^t},{h_{t - 1}}} \right] + {b_c})$

(8)

其中, ${W_i}$ 和 ${W_c}$ 指的是权值, ${b_i}$ 和 ${b_c}$ 指的是偏置值. 之后由记忆单元 ${C_t}$ 表示该LSTM的cell更新状态:

${C_t} = {i_t} \cdot \tilde C + {f_t} \cdot {C_{t - 1}}$

(9)

最后确定LSTM单元的输出数据信息 ${h_t}$ 为:

${o_t} = \sigma \left( {{W_o}\left[ {{p^t},{h_{t - 1}}} \right] + {b_o}} \right)$

(10)

${h_t} = {o_t} * \tan \left( {{C_t}} \right)$

(11)

其中, ${o_t}$ 是输出门; ${h_t}$ 是当前神经元在时间的输出. 具体的推导公式可参考文献[19]. 通过上述记忆单元 ${C_t}$ 保留经历过遗忘和输入的信息实现了LSTM单元有效传递时间间隔较远的历史信息从而获取数据内在时间相关性特征. 本文所提LSTM层由32个cell组成处理时序信号表示为一维特征向量如式(12)所示.

$s = \left[ {{h^1}, \cdots ,{h^t}} \right], t \in \left\{ {1, \cdots ,32} \right\} $

(12)

特征向量s进入由6个cell组成的全连接层处理, 其输出为:

$h = f\left[ {Ws + \varepsilon } \right]$

(13)

其中, W为全连接层的权值矩阵; $\varepsilon $ 是偏置项向量. 我们将全连接层的激活函数设置为Softmax函数, 则最终输出为:

$v_i^ * = \frac{{{e^{{v_i}}}}}{{\displaystyle\sum {{e^{{v_i}}}} }},i \in \left\{ {1, \cdot \cdot \cdot ,6} \right\}$

(14)

通过式(14)最大概率识别步态模式 ${v_i}$ .

从上述分析可知, 本文所提CNN-LSTM模型充分融合CNN和LSTM两者获取步态时间序列数据内在最具代表性的时间、空间步态特征的优异特性, 降低其学习网络结构复杂性和模型较大训练开销, 增强融合深度学习算法非线性拟合性能, 有助于提升本文所提模型步态分类的精确度和准确度.

本文所提神经网络模型采用分类交叉熵损失函数最小化训练样本的分类错误率, 其定义为:

$L\left( {X,D,B} \right) = - \frac{1}{N}\sum\limits_{i = 1}^N {\left\langle {{y^{\left( i \right)}},\log {{\hat y}^{\left( i \right)}}} \right\rangle } $

(15)

其中, D表示训练集, W表示权值矩阵, B表示偏置值; N表示训练样本的数量, ${y^{\left( i \right)}}$ 表示的是第i个样本的标签, $\hat y$ 表示预测的标签以及 $\left\langle \cdot \right\rangle $ 表示内积.

2 实验与结果分析 2.1 实验数据获取

本文采用的是加州大学欧文分校(University of California Irvine)提出的用于机器学习的UCI数据库中的HAR数据集. 该数据集收集了30名年龄在19至48岁的志愿者的6种步态模式: 站立、坐着、躺下、行走、在楼上和楼下行走. 每个受试者执行两次实验方案: 第一次实验将智能手机(内置加速度计和陀螺仪)佩戴于腰部左侧; 第二次实验, 受验者随意放置智能手机. 要求受验者在实验室环境下以自己舒适的步速完成不同步态行走, 便于获得较真实行走步态数据集. 采样频率设置为50 Hz采集三轴加速度和角速度步态行走数据.

2.2 数据预处理

为有效消除噪声干扰获取蕴含更多有用步态数据, 本文采用中值滤波器和三阶低通Butter-worth滤波器(截止频率设置为0.3 Hz)对人体加速度信号和重力加速度信号消噪处理. 设置窗口宽度为2.56 s进行滑窗采用数据, 窗口重叠设置为50%, 即每个窗口有: 2.56 s×50 Hz=128 周期, 采用快速傅里叶变换获取17个步态数据时域、频域步态特征. 为此, 文中采用了17个度量标准评估时域和频域的特征向量, 即总共提取了561个特征来描述每个活动窗口(样本点), 每个样本点看作为一种步态模式, 其度量标准如表1所示.

2.3 步态分类性能评价标准选取

为客观、准确评价本文所提步态分类模型的泛化性能, 本研究选取步态分类相关研究常用的分类准确率、步态精确率、召回率作为步态分类性能客观评价指标.

(1)准确率(Accuracy): 用于客观评价本文所提步态深度学习分类模型的精确度, 其定义为:

$Accuracy = \frac{{TP + TN}}{{TP + FP + TN + FN}}$

(16)

其中, TP表示正确识别步态模式的样本数; FP表示错误识别步态模式的样本数; TN表示正确步态模式错误识别为其他步态模式的样本数; FN表示步态模式错误识别为正确步态模式的样本数.

(2)步态精确率(Precision): 用于客观评价本文所提步态深度学习分类模型“真正”鉴别步态模式的性能, 其定义为

$Precision = \frac{{TP}}{{TP + FP}}$

(17)

(3)召回率(Recall):用于客观评价本文所提步态深度学习分类模型步态模式正确识别的性能, 其定义为

$Recall = \frac{{TP}}{{TP + FN}}$

(18)

2.4 实验结果

本文实验是基于谷歌开源的深度学习框架Tensorflow实现, 具体的实验平台为CPU(i5), Python3.7, Keras2.3, Tensorflow2.1. 选取样本数10299, 随机选取70%为训练集、30%为测试集, 实验数据分批送入模型训练, 批处理块大小为32个数据样本. 模型的训练回合数设置为30且采用了自适应学习率优化算法Adam且学习率设置为0.001.

(1)步态深度学习分类模型最优结构参数选取

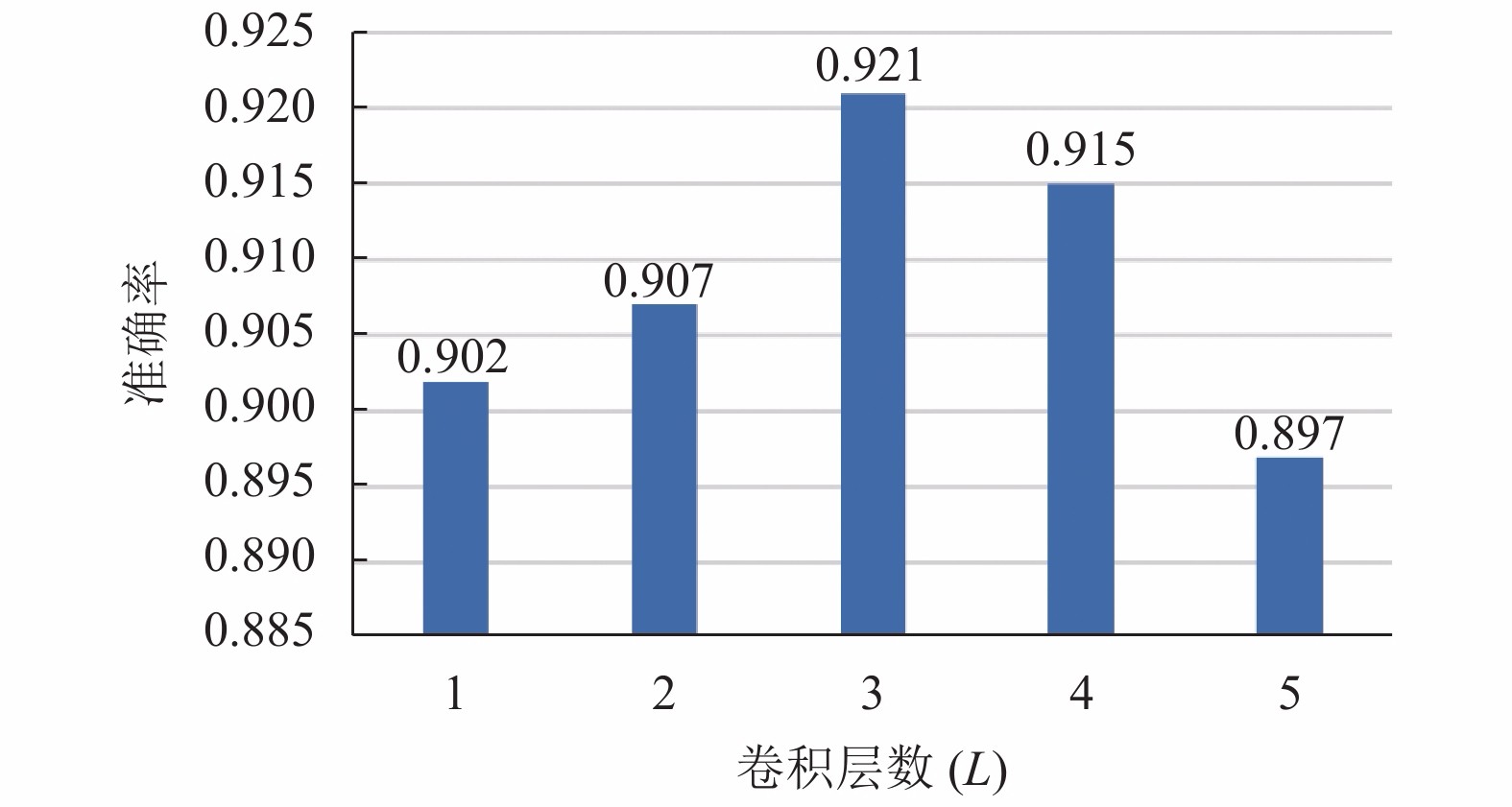
为准确优化设计本文所提步态深度学习分类模型结构, 提高其性能, 本文首先量化评估所提模型优化选取卷积神经网络部分的卷积层数和长短期记忆网络中神经元数量. 卷积神经网络卷积层数选取结果如图2所示, 从图2可以看到, 当卷积层数从1增长到3时, 模型的准确率逐步增大, 当卷积层数为3时, 分类准确率最大, 可达92.1%, 但卷积层数增至4和5时, 分类准确率显著下降, 结果表明, 当卷积层数为3时, 本文所提步态融合深度学习分类模型可从可穿戴传感加速度和陀螺仪步态数据中获得蕴含更多与步态模式变化密切相关的步态特征信息, 有效提升模型的分类性能, 而卷积层数增至4和5时, 难以从可穿戴传感步态数据中获得一些代表性特征信息, 可能丢失一些有用步态特征信息, 降低模型的分类性能.

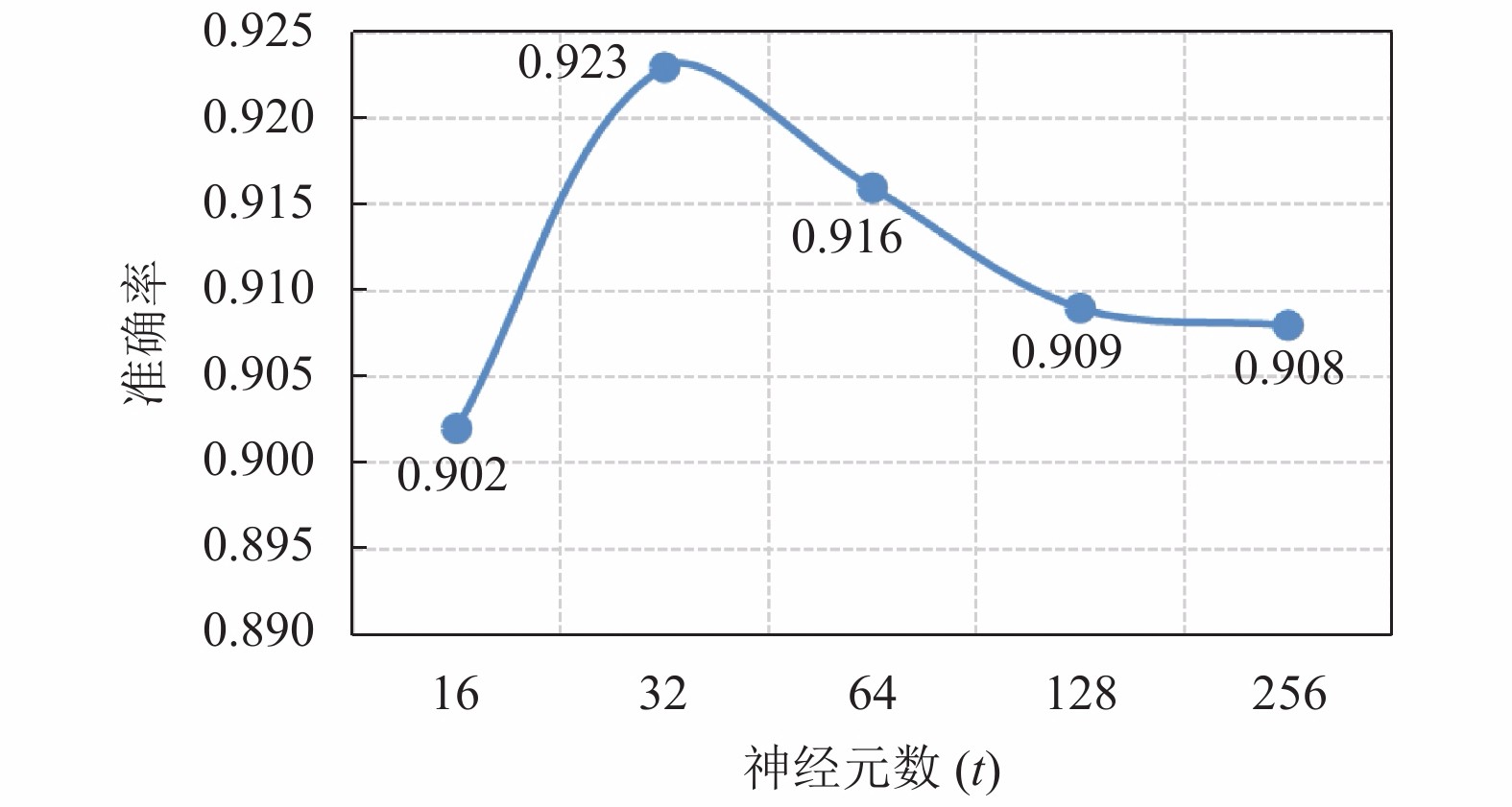
选取最优LSTM模型的神经元数的结果如图3所示, 从图3可以看到, 当神经元数从16增至256过程中, 选取不同神经元数影响模型步态模式分类性能. 当神经元数为32时, 分类准确率最大, 可达92.3%, 当神经元数从32增至256时, 分类准确率显著下降. 结果表明, 神经元数选取32时, 本文所提模型可从可穿戴传感步态数据空间局部特征获得更多与步态变化密切相关的时间相关特征信息, 显著提升本文所提模型步态分类性能.

(2) CNN-LSTM模型步态分类性能评估结果

本文所提CNN-LSTM步态深度融合学习模型基于所取最优参数的分类性能评价结果如表2所示, 从表2可以看到, 本文所提模型能以较好分类性能鉴别6种不同步态模式, 平均准确率可达91.45%、平均召回率可达91.53%; 比较而言, “躺”步态模式具有最高准确率, 可达99%, 表明本文所提深度融合学习模型能够有效从可穿戴传感加速度、陀螺仪步态数据获取与“躺”步态模式密切相关的时-空步态特征信息, 有效提高其模式鉴别性能. 然而, “站立”步态模式准确率最低, 仅为80.94%, “坐”步态模式召回率最低, 仅为81.06%, 这些结果表明, 本文所提模型难以从可穿戴传感加速度、陀螺仪步态数据获取与“坐”、“站立”步态模式密切相关的时-空步态相关特征信息, 这可能由于本文所取步态数据采集过程可穿戴单传感步态采集器佩戴人体解剖部位难以捕获“坐、站立”步态模式相关信息.

另外, 基于相同的步态数据, 本文选取基于传统机器学习算法(诸如决策树、KNN、支持向量机等)构建的步态分类模型, 进一步评价本文所提模型的优越性能, 其比较分类性能如表3所示, 从表3可以看到, 本文所提步态深度融合学习模型的准确率、精确率、召回率最高, 均可达91.5%; 其次, KNN步态分类模型准确率、精确率、召回率均约为90%; 支持向量机准确率、精确率、召回率均低于90%, 而决策树步态分类模型准确率、精确率、召回率最低, 仅为86%, 上述结果表明, 本文所提CNN-LSTM步态深度融合学习模型分类性能明显优于传统机器学习步态分类模型性能, 其根本原因在于本文所提模型能够充分利用CNN、LSTM深度融合学习算法所具获取数据最具代表性特征的优异特性, 有效从可穿戴传感加速度、陀螺仪步态数据获取最具代表性的时-空相关性步态特征, 显著提升步态分类性能, 而传统机器学习步态分类模型基于线性模型仅可获取局部空间、时间步态特征, 难以从可穿戴传感加速度、陀螺仪时序步态数据获取最具代表性的时-空相关性步态特征, 影响其分类性能.

此外, 为进一步评价本文所提模型的有效性, 基于上述相同步态数据, 将本文所提模型与其他传统深度学习模型(诸如CNN、RNN^[20]、LSTM、GRU^[21]等模型)进行比较, 其比较结果如表4所示. 从表4可以看出, 本文所提CNN-LSTM模型步态分类性能明显优于其他传统深度学习步态分类性能. 就比较而言, RNN网络模型步态分类性能较差, 其准确率、精确率、召回率仅均约为70%, 其原因在于RNN网络学习模型难以获取步态时间序列内在最具空间、时间相关性步态特征信息; CNN、GRU和LSTM三个学习模型的准确率、精确率、召回率均约为88%, 其步态分类性能虽优于RNN网络学习模型步态分类性能, 但明显低于本文所提CNN-LSTM融合学习模型的步态分类性能, 其根本原因在于: 基于传统CNN深度学习的步态分类模型仅能获取步态时间序列数据内在最具代表性的局部空间步态特征信息; 基于传统LSTM、GRU深度学习的步态分类模型仅能获取可穿戴步态时间序列数据内在最具代表性的时间相关性步态特征信息, 上述两种传统深度学习步态分类模型局限在于难以获取可穿戴步态时间序列数据内在最具代表性的时间-空间相关性步态特征信息, 而本文所提CNN-LSTM融合深度学习步态分类模型可充分融合CNN、LSTM各具获取步态时间序列内在空间、时间相关性特征信息优异特性, 有效获取可穿戴步态时间序列数据内在最具代表性的时间-空间相关性步态特征信息, 弥补传统CNN、LSTM深度学习模型获取步态时间序列数据内在最具代表性步态特征信息的局限, 有效提升基于可穿戴步态传感数据的步态分类性能.

3 结论

本文提出了一种基于可穿戴传感数据的步态模式深度学习融合判别新模型, 该模型能够充分融合卷积神经网络和长短时记忆神经网络深度学习模型所具获取数据最具时空代表性特征的优异特性, 有效从可穿戴传感加速度、陀螺仪步态数据获取最具代表性的时-空相关性步态特征, 显著提升可穿戴步态模式分类性能, 为进一步深入开展可穿戴多传感步态模式深度学习分类相关研究提供可靠借鉴.