1 引言

网约车是当今社会的主要出行方式之一, 为人们的生活带来了便捷, 然而这一行业也存在许多问题, 如乘客等待时间长, 司机空车率高^[1]. 造成这些问题的主要原因是网约车调度不合理, 过多的车辆集中在繁忙区域导致车辆的供给大于需求, 而在较为偏远的地区, 网约车数量极少, 分布极为稀疏^[2]. 网约车需求预测可以有效应对这一问题, 通过预测区域内网约车的需求, 提前引导司机前往不同的区域, 从而避免出现网约车分布不均匀的问题^[3].

网约车需求预测是智能交通系统的重要组成部分, 也是交通大数据分析的一项难题, 这是因为其受到多种时空因素的共同影响, 单一因素的建模方式很难实现准确的预测. 目前研究人员提出了许多方法来解决这一问题, 大致可以分为机器学习和深度学习两类, 前者需要的训练数据较少但准确率较低, 后者则恰好相反. 其中机器学习的方法主要有线性回归^[4]和支持向量回归^[5]; 深度学习的方法有卷积神经网络(CNN)^[6]、卷积神经网络与长短时神经网络(LSTM)相结合^[7]和图卷积神经网络(GCN)^[8]. 但这些方法考虑的影响因素不足, 仍然无法避免模型不完善的问题. 在时间因素方面, 出租车需求预测会受季节、节假日和工作时间的影响; 同时历史的出行信息也会有一定的影响, 这是因为乘客在到达目的地后, 大概率会在一段时间后从目的地再次出发前往下一个区域. 在空间因素方面, 出租车需求预测在空间上受到地理位置的限制; 同时不同的地理位置可能具有相似的社会意义也会影响出租车的需求.

针对上述问题, 本文提出了一种多图时空图卷积网络(MGSTGCN), 以提高网约车需求预测的准确性. 该网络在空间上使用图卷积神经网络进行特征捕获, 针对不同地区的地理位置属性、交通起止点(OD)属性和社会意义相似性建立了3种图, 随后进行聚合; 在时间上使用长短期记忆网络(LSTM). 最后使用了成都网约车轨迹数据和曼哈顿区出租车数据对所建立网络进行验证.

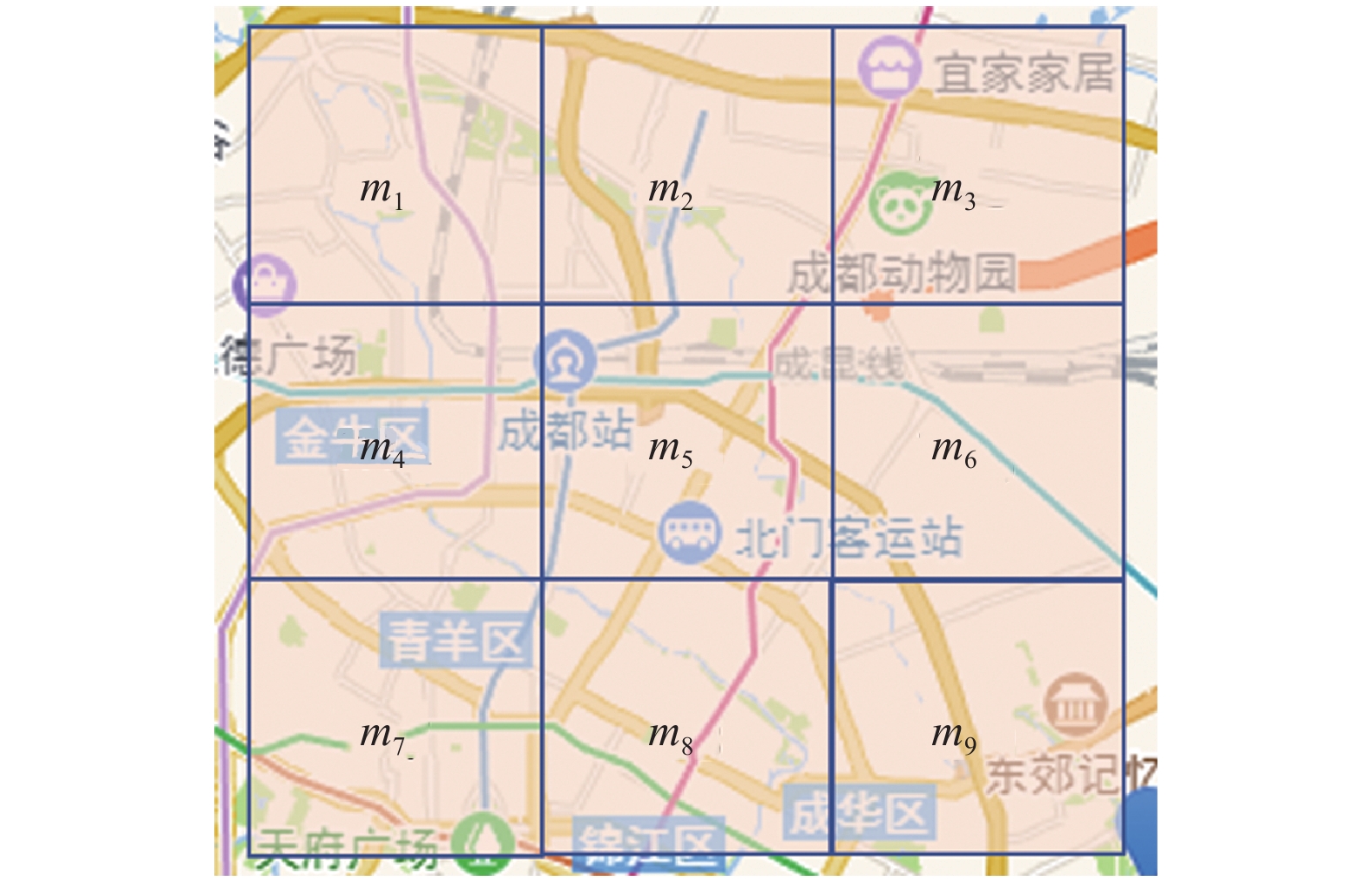
2 算法框架 2.1 出租车需求预测建模

本文采用了交通领域的经典处理方法^[9], 将待处理区域平均分为多个网格, 若将网格分为9个, 每个网格由最大坐标与最小坐标定义, 如图1所示, 通过这样的方式, 研究每个小格子区域内的出租车需求. 随后将每个格子看作图的一个顶点, 用于构建出租车需求预测的图模型.

在空间建模方面, 文献[10]考虑了地理位置因素和OD的影响, 本文则在此基础上研究了不同区域的社会属性对预测问题的影响, 包括商业街、大学城、工业园等, 通过研究发现, 即使相隔距离很远, 具有相似社会属性的地区在交通流上具有高度相似性. 最终本文采用地理位置因素、OD因素以及社会属性因素分别构筑了地理图、OD图和社会属性图.

在时间建模方面, 则考虑历史出行特征, 通过LSTM和注意力机制进行时间特性的捕获, 来掌握时间维度上的出租车需求变化, 可以预测每对网格间的需求.

2.2 空间网络模型 2.2.1 空间建模

以图1划分为例, 将每个网格看作一个图的节点, 本文在此基础上建立了3种图来捕获空间特征, 如图2所示. 其中, 图2(a)为地理图结构, 将每个网格的中心点视作网格的地理位置中心, 中心点的距离视作地理图结构的边权值. 设中心距离的单位为u, 那么网格8和9之间距离记作 $dist({m_{{\rm{ }}8}},{m_{{\rm{ }}9}}) = u$ , 网格8和4之间距离记作 $dist({m_{{\rm{ }}8}},{m_{{\rm{ }}4}}) = \sqrt 2 u$ , 距离越近权值则越小, 两者间的出租车需求也会有一定的相似性, 可将地理图范围集 ${\varphi _i}$ 定义为式(1):

$ {\varphi _i} = \left\{ {{m_j}|dist({m_i},{m_j}) \le L} \right\} $

(1)

其中, L为可设定阈值.

图2(b)为OD图结构, 本文使用了OD矩阵来对OD图进行定义: 只要任意两个顶点间有出租车需求存在, 那么它们就是相关的. 同时, OD图会受时间因素的影响, 这是因为在不同的时间段内, 两个区域间的OD信息常常是不同的, 所以建模时要考虑到不同时间下OD图的变化情况.

本文假定两个地区社会属性相似, 相距距离较大, 则此时在地理图和OD图上, 这两个地区的关联度较小, 但由于社会属性的相似性, 两个地区的出租车需求相似性较高. 为了应对这种情况, 本文设计了社会属性图, 其结构如图2(c)所示. 本文将每个网格的社会属性分为: 工业、生活、出行、商业、娱乐和住宿, 每个栅格的社会属性由其所包括的非地理意义点(POI)的属性所决定.

本文爬取了成都部分地区的POI点, 将每个栅格内的POI点进行了社会意义分类, 栅格的社会属性与相同属性最多的POI点保持一致, 随后在建立图结构时, 应用动态时间规划法(DTW), 来量化社会属性相似的网格间的相似度, 公式如式(2)所示:

$ {S_{i,j}} = \left\{ \begin{split} & \exp ( - DTW({F_i},{F_j})),\;\;i \ne j \\ & 1,\;\;i = j \\ \end{split} \right. $

(2)

其中, ${F_i} \in {\mathbb{R}^{1 \times T}}$ 表示离开第i个网格的出租车流出向量, T为向量长度, 由所选定的对照时间尺度所决定. 得到矩阵S后对其进行归一化即可得到社会属性图的权重.

2.2.2 图模型聚合器

如果将每种图模型单独进行训练会大大提升算法的复杂度, 为避免这一缺点, 本文在传统聚合函数的基础上进行改进^[11], 综合考虑了3种图模型对预测结果的不同影响程度, 设计了一种图聚合器. 地理图的聚合器方式如式(3)所示:

$ l_{t'}^i = \sigma \left( {{W_l} \cdot \left( {f_{t'}^i + \sum\limits_{{m_j} \in {\varphi _{_i}}} {\frac{{dis{t^2}({m_i},{m_j})}}{{\displaystyle\sum {dis{t^2}({m_i},{m_j})} }}} } \right)f_{t'}^j} \right) $

(3)

其中, $l_{t'}^i$ 表示时间 $t'$ 时的地理图嵌入矢量; ${W_l}$ 是可训练的权重矩阵; 而 $f_{t'}^i$ 和 $f_{t'}^j$ 分别是地理聚合操作之前的 ${m_i}$ 和 ${m_j}$ 的特征. 同理可进行出OD图和社会图的特征聚合, OD图的特征聚合如式(4)所示:

$ p_{t'}^i = \sigma \left( {{W_p} \cdot \left( {f_{t'}^i + \sum {\frac{{nu{m^2}({m_j})}}{{\displaystyle\sum {nu{m^2}(m{}_j)} }}} } \right)f_{t'}^j} \right) $

(4)

式中, $num({m_j})$ 表示于 ${m_j}$ 开始或结束的需求量, ${W_q}$ 是可训练的权重矩阵. 而 $p_{t'}^i$ 表示时间 $t'$ 下的OD图嵌入矢量, $f_{t'}^i$ 和 $f_{t'}^j$ 分别是OD聚合操作之前的 ${m_i}$ 和 ${m_j}$ 的特征.

社会图的特征聚合如式(5)所示:

$ q_{t'}^i = \sigma \left( {{W_q} \cdot \left( {f_{t'}^i + \sum {\frac{{{S^2}({m_i},{m_j})}}{{\displaystyle\sum {{S^2}({m_i},{m_j})} }}} } \right)f_{t'}^j} \right) $

(5)

式中, $S({m_i},{m_j})$ 表示 ${m_i}$ 和 ${m_j}$ 的社会属性相似度, $q_{t'}^i$ 表示时间 $t'$ 下的社会图嵌入矢量, ${W_q}$ 是可训练的权重矩阵 $f_{t'}^i$ 和 $f_{t'}^j$ 分别是社会属性聚合操作之前的 ${m_i}$ 和 ${m_j}$ 的特征.

将3种聚合器加以整合即可得到图的最终聚合表示:

$ G_{t'}^i = \left[ {o_{t'}^i,p_{t'}^i,q_{t'}^i} \right] $

(6)

2.3 时空网络架构

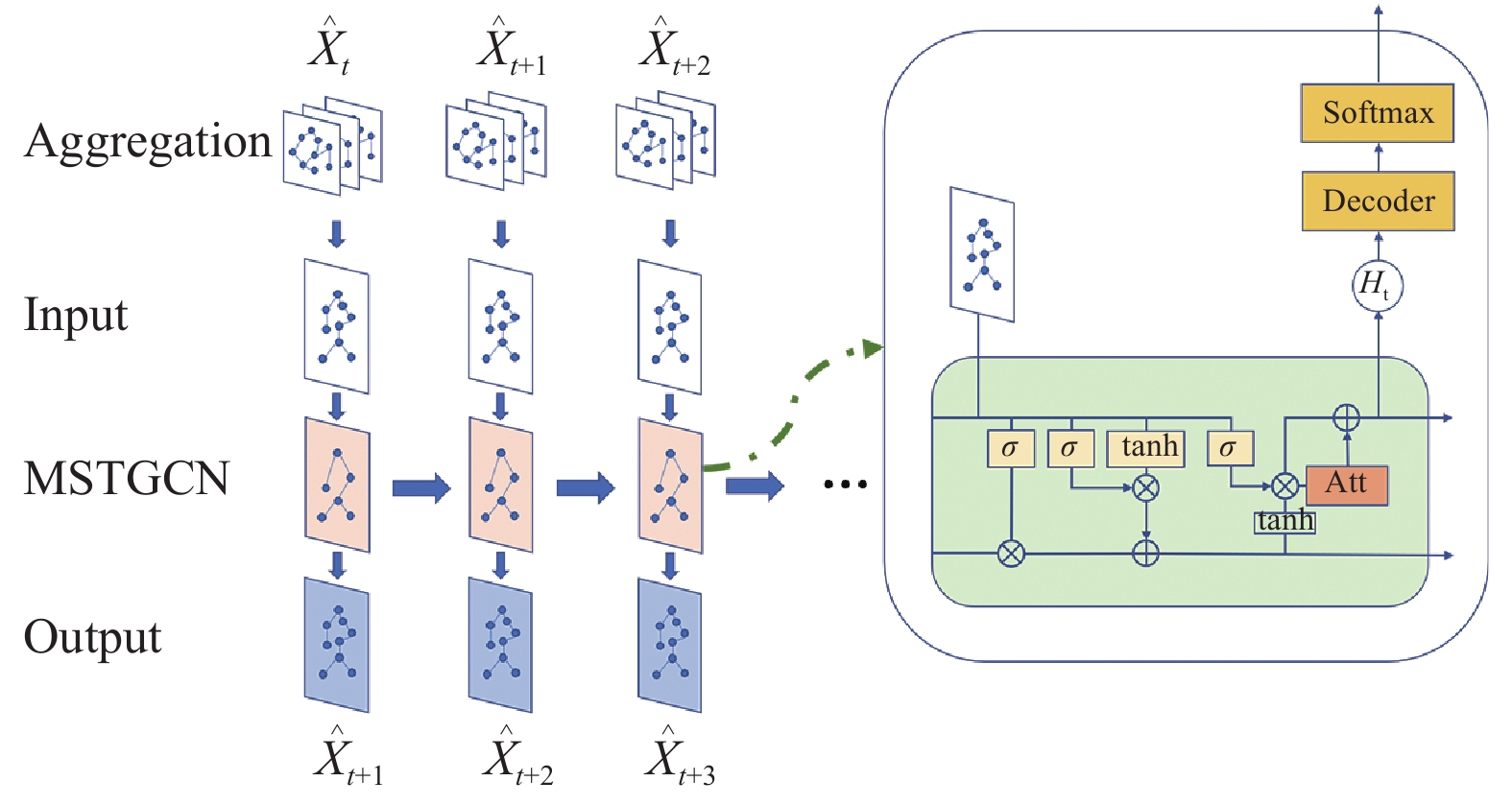
MGSTGCN的时间架构部分与LSTM一样都有LSTM的输入门、忘记门和输出门, 但均由图卷积算子而得, 且引入了注意力机制, 其中时间序列为输入. 时间结构与空间结构相结合构成了MGSTGCN网络, MGSTGCN的层结构如图3所示.

注意力机制的引入目的是增强关键节点的信息, 如式(7)所示:

$\left\{ \begin{split} & {f_t} = \sigma ({W_f}[{h_{t - 1}},{x_t}] + {b_f}) \\ & {i_t} = \sigma ({W_i}[{h_{t - 1}},{x_t}] + {b_i}) \\ & {o_t} = \sigma ({W_o}[{h_{t - 1}},{x_t}] + {b_o}) \\ & {c_t} = {f_t} \odot {c_{t - 1}} + {i_t} \odot \tanh ({W_c}[{h_{t - 1}},{x_t}] + {b_f}) \\ &{{\hat h }_t} = {o_t} \odot \tanh ({c_t})\\ &{h_t} = {f_{\rm att}}\left( {{{\hat h }_t}} \right) + {{\hat h }_t}\\ \end{split}\right. $

(7)

其中, $\sigma ( \cdot )$ 为sigmoid函数, $ \odot $ 为同或运算符, $i,\;f,\;o,\;c$ 分别代表输入门, 遗忘门, 输出门和细胞状态向量. 当它们中的每一个都被更新时, 有相应的可训练权重W和偏差向量b, ${f_{\rm att}}$ 代表注意力网络, 可以在增强关键节点信息的同时保证信息的完整性, ${f_{\rm att}}\left( {{{\hat h} _t}} \right)$ 所得为注意力矩阵. 注意力矩阵设为 $V = ({V_1},{V_2},\cdots,{V_t},\cdots,{V_N})$ , ${V_t}$ 为列向量, 计算公式如式(8)所示.

$ {V_t} = softmax\left( {K\tanh \left( {W{ \hat h _t} + b} \right)} \right) $

(8)

式(8)中, 通过 $softmax( \cdot )$ 函数进行归一化, 得到注意力矩阵V. ${V_t}$ 在语义上理解为输出时刻t时, 节点间的相互依赖程度向量.

3 实验 3.1 数据集处理

本文选用数据集为成都市局部区域的滴滴快专车平台的轨迹数据和纽约市曼哈顿区出租车数据集.

其中成都市数据集的时长为2016年11月1日至11月30日, 该数据集来自于滴滴公司的盖亚数据开放计划, 轨迹点的采集间隔是2–4 s. 轨迹点经过了绑路的处理, 保证了数据都能够对应到实际的道路信息. 司机及订单信息进行了加密脱敏匿名化处理. 纽约市曼哈顿区出租车数据集的时长为2018年7月1日至7月30日. 本文分别选取前20天数据作为训练集, 后10天数据作为测试集.

3.2 评估指标

本文选取的评估指标为均方根误差(RMSE)和对称平均绝对百分比误差(SMAPE), 用以评估预测准确性. RMSE和SMAPE的计算公式如式(9)和式(10)所示:

$ RMSE = \sqrt {\frac{1}{{\left| {\left. {{M_{t + 1}}} \right|} \right. \times N}}\sum\limits_{n = 1}^N {\left. {\left\| {M_{t + 1}^n - } \right.\hat M_{t + 1}^n} \right\|} } $

(9)

$ SMAPE = \frac{2}{{\left| {\left. {{M_{t + 1}}} \right|} \right. \times N}}\sum\limits_{n = 1}^N {\sum\limits_{m \in M_{t + 1}^n} {\frac{{m - \hat m}}{{m + \hat m + 1}}} } $

(10)

3.3 实验结果

为证明模型的有效性和准确性, 本文选取了4种主流模型与本文算法进行对照试验, 分别是: HA^[10]、LSTNet^[11]、GCRN^[12]、GEML^[8]、MGSTGCN. 实验结果如表1所示.

同时为检验该模型的稳定性, 本文选取了32, 64, 128, 256, 512的网格维度与模型进行了对照实验, 以GEML模型为例, 实验结果如图4所示. 可以看出在不同的网格维度下, 该模型的算法性能均优于GEML模型, 且维度越高, 划分越精密, 该模型的优越性越明显.

4 结论

本文提出了多图时空图卷积神经网络来解决网约车需求预测问题, 该网络将区域网格看作图的顶点, 结合了地理属性、出入流属性和社会属性构建空间图模型, 结合历史出行规律构建时间模型, 并引入了注意力机制, 从而可以有效地预测区域内的出租车需求. 成都市局部区域的滴滴快专车平台的轨迹数据和纽约市曼哈顿区出租车数据集用于训练和测试, 实验结果表明, 该模型的RMSE和SMAPE指标均优于其余主流模型, 其中相较于GEML模型, 在成都市和曼哈顿区的数据集上, MGSTGCN的RMSE指标分别降低了16.03%和15.46%, SMAPE指标分别降低了11.57%和4.77%, 且随着网格维数的增加, 本文算法的优越性越明显, 可以更有效地进行网约车需求预测.

进一步还需要探索的问题是找到更好的网格划分标准, 同时再结合网约车的营收数据, 扩展模型功能, 有效提高网约车的运营效率和营收情况.