2. 国电南瑞南京控制系统有限公司, 南京 210023
2. Guodian NARI Nanjing Control System Co. Ltd., Nanjing 210023, China
近年来, 能源短缺和环境污染, 成为人类发展所面临的巨大挑战[1-3]. 为了减少碳排放, 降低化石能源消耗对国家能源安全构成的威胁, 缓解环境危机, 加速开发和推广应用新能源车辆已成为全球共识, 新能源汽车和轨道交通车辆被列入我国七大战略新兴产业, 也是“中国制造2025”的重要组成部分. 作为新能源车辆的关键技术, 动力电池及其应用是各国竞相占领的技术制高点, 对自主突破新能源车辆技术瓶颈至关重要. 为了电动汽车安全平稳运行费, 保障动力电池的安全稳定是重中之重. 对此, 需要研究电动汽车充电过程故障在线预警方法, 保证充电过程安全性, 而且实现电池充电时间的最小化.
国内外车企在电池安全管理方面具备一定成果. 文献[4]主要对电动汽车充电过程中的故障现象进行分析, 并给出了一些诊断方法. 文献[5]划分了不同的动力电池故障等级, 通过算例验证故障检测方法. 文献[6]通过对动力电池故障数据进行数据转换, 运用神经网络的方法对动力电池故障进行短期预测. 文献[7]研究一种实时故障诊断与失效处理策略, 实时诊断可能发生的故障并根据故障的严重程度采取合适的失效处理策略. 文献[8]研究了电动汽车充电控制原理, 给出了常见无法充电故障检测与维修的方法. 针对电动汽车充电故障在线诊断, 许多学者仅仅是分析了电动汽车动力电池的故障等级, 并给出了一种常规的手工操作的故障诊断方法, 并没有对动力电池故障进行一个短期和中长期的在线诊断与预警, 因此如何将短期和中长期的动力电池在线诊断与预警成果应用于实车监控就显得尤为重要.
本文以电动汽车充电过程的动力电池为对象, 针对充电安全问题, 分析单体电池基本性能, 为了准确清晰的表征电池电压的变化趋势, 采用“电压差归一化曲线”来进行分析动力电池组安全特性, 以短期和中长期不同时间尺度为依据制定安全充电控制策略, 主要研究了电池充电温升因素影响下的中长期充电控制策略, 并建立目标函数, 利用遗传算法进行优化控制, 最后利用充电桩监控平台提供的充电状态信息数据, 对所提出的基于电池模型的充电设施充电数据在线预警进行了验证.
1 电动汽车动力电池充电安全特性分析 1.1 单体电池基本性能研究针对充电安全问题, 搭建电池测试平台, 以典型锂离子电池(三元电池和磷酸铁锂电池)为研究对象, 分析不同温度、充电倍率、充电电压等对电池热稳定性和负极析锂的影响.
对单体电池进行容量测试实验和混合脉冲功率特性实验, 来分析单体电池的基本特性. 两款电池的容量测试结果如图1, 图2所示. 图3, 图4为电池开路电压与内阻随SOC变化的关系.

|
图 1 磷酸铁锂电池容量测试结果 |

|
图 2 三元电池容量测试结果 |

|
图 3 磷酸铁锂电池开路电压与内阻随SOC变化 |
根据对单体电池的基本特性研究结果的出, 开路电压随SOC的变化情况, 形成电池充电安全的边界条件, 可以为动力电池充电安全系数的制定及预警提供理论依据.

|
图 4 三元电池开路电压与内阻随SOC变化 |
1.2 动力电池组充电安全特性分析
造成不同电池单体电压差异的原因是多样的, 其中主要关注的影响因素是电池的容量、内阻及放电区间.
本文基于电池单体SOC-V曲线对充电阶段电池电压变化趋势进行判别. 但是由于锂离子电池存在电压平台, 电池处于平台区时, 电池电压的差异可能很小, 仅利用SOC-V曲线很难进行判断. 为了准确清晰的表征电池电压的变化趋势, 采用“电压差归一化曲线”来进行分析. 以充放电过程中SOC作为横坐标, 形成曲线的公式为:
| $ diff(SOC) = \frac{{V(SOC) - {V_{\min }}(SOC)}}{{{V_{\max }}(SOC) - {V_{\min }}(SOC)}} \times 100{\text{%}} $ | (1) |
其中, V(SOC)、Vmin(SOC)、Vmax(SOC)分别表示对应SOC的选定单体电池的电压、最低单体电压、最高单体电压. 对于一个完整的充放电过程, 取任意的单体电池, 曲线都是在0~100%之间变化. 通过对比参考曲线即可分析出选定单体电池的电压变化趋势, 参考曲线选定电池电压中位数的“电压差归一化曲线”[9,10], 即:
| $dif{f_{\rm ref}}(SOC) = \frac{{{V_{\rm mid}}(SOC) - {V_{\min }}(SOC)}}{{{V_{\max }}(SOC) - {V_{\min }}(SOC)}} \times 100{\text{%}} $ | (2) |
其中, Vmid(SOC)是对应SOC的所有电池单体电压的中位数. 选取中位数作为参考标准, 是为了防止电池组中异常偏高和偏低的电池对参考标准造成影响. 如图5所示的是一次充电过程中某一单体电池“电压差归一化曲线”与参考曲线的对比.
“电压差归一化曲线”作为普通统计方法的扩展和补充, 不仅增强了异常电池诊断的精度, 同时这种方法简单易行, 可以应用于每一个电池单体, 使异常电池的定位更加直观.
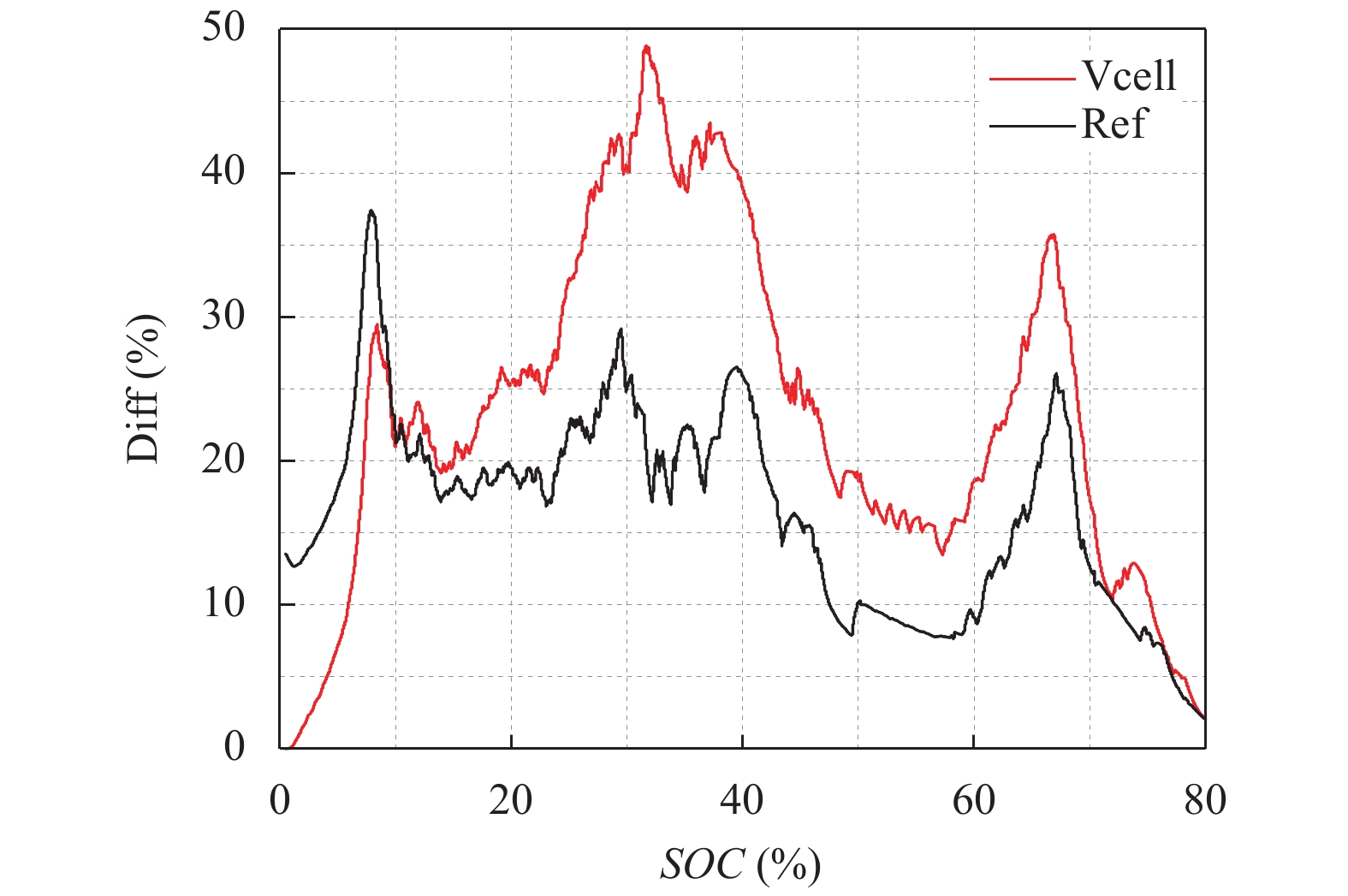
|
图 5 电压差归一化曲线 |
2 多时间尺度的电动汽车动力电池智能充电策略 2.1 短期安全智能充电策略
常见的故障现象包括: 电池组容量降低、充电电压过高、电池组充不进电、放电电压低; 电池自放电大; 局部高温、单体电压一致性变差、电池打弧击穿等.
图6展示了短期充电安全智能保护策略流程图. 该策略通过实时检测锂离子电池的充放电电流、单体电压、电池组总电压以及环境温度等数据, 并根据这些数据对动力锂电池可能存在的故障进行判断, 给出相应的处理措施, 避免锂电池发生严重故障和事故, 并将数据上传至云服务器处理, 以便长期安全预警[9,10]. 需要采集的电池数据有:
(1)单体电池的电压;
(2)单体电池的极耳温度;
(3)电池组总电压;
(4)充放电总电流.
2.2 中长期安全智能充电策略基于充电极化电压特性的锂电池可接受充电电流曲线如图7所示, 随着电池SOC的增加, 可接受充电电流逐渐减小. 随着电池SOC的增加, 欧姆内阻、极化内阻和熵变系数会随之变化, 造成不同SOC区间的充电温升速率不同, 因此, 在基于极化特性的可接受充电电流的限制下, 在温升速率小的区间提高充电电流, 在温升速率大的区间降低充电电流, 从而实现全程充电时间和充电温升的平衡, 在保证充电速度的前提下延长电池使用寿命. 因此本节提出以缩短充电时间和限制充电温升作为优化目标的优化充电策略(时间-温升策略): 以△SOC为间隔划分充电SOC区间, 共分为N步, 在极化限制的可接受充电电流曲线约束下, 合理优化选择每一步的充电电流, 使得优化充电目标函数取得最优值. 因为温升与电池寿命相关, 因此目标函数综合考虑了充电时间和寿命, 将已由充电时间和充电温升组成.

|
图 6 短期充电安全智能保护策略流程图 |

|
图 7 极化限制可接受充电电流曲线及容量温升充电策略示意图 |
每隔一定△SOC变化一次充电电流, 假设从0%SOC充电到充电100% SOC需要N步变化电流. 不考虑预充电情况下, N和SOC之间的关系为式(3).
| $N = \frac{{100}}{{\Delta SOC}}$ | (3) |
第k步充电时间tk为:
| $ {t}_{k}=\frac{{Q}_{k}}{{I}_{k}}=\frac{\Delta SOC·Q}{{I}_{k}}$ | (4) |
其中, 电池充电容量Q以0.05C充电容量为基准.
总充电时间t为:
| $t = \sum\limits_{k = 1}^{N - 1} {{t_k}} + {t_N} = \sum\limits_{k = 1}^{N - 1} {{t_k}} + \frac{{{Q_N}}}{{{I_N}}}$ | (5) |
总充充电容量Qch为:
| $ {Q}_{ch}=\Delta SOC·Q·(N-1)+{Q}_{N}$ | (6) |
在此把第N步充电容量和充电时间单独提出来讨论, 因为第N步充电容量不一定能达到理论值
| ${I_N}R + k{I_N} + b + OCV(N) = 4.2\;{\rm{V}}$ | (7) |
则
| $OCV(N) = 4.2 - ({I_N}R + k{I_N} + b)$ | (8) |
根据OCV-SOC曲线可以求解出第N步充电结束时的SOCN为:
| $SO{C_N} = {f^{ - 1}}(4.2 - {I_N}R - k{I_N} - b)$ | (9) |
则第N步充入的容量为:
| $ {Q}_{N}=Q·[SO{C}_{N}-\Delta SOC(N-1)]$ | (10) |
第N步充电时间也可求.
关于充电温升的函数关系如下:
| $\begin{split} cm\left( {{T_k} - T_k^{st}} \right) = &\int_0^{{t_k}} {I_p^2R{\rm{d}}t} + \int_0^{{t_k}} {I_p^{}{U_p}{\rm{d}}t} \\ &\!+\int_0^{{t_k}} {{T_{CELL}}\Delta S\frac{1}{{nF}}{\rm{d}}t} -\! \int_0^{{t_k}} {hA({T_p} - {T_{air}}){\rm{d}}t} \\ \end{split} $ | (11) |
式中,
| $T_{k + 1}^{st} = T_k^{\rm end}$ | (12) |
温升为充电过程中的最大温度-初始温度:
| $\Delta T = {T_{\max }} - T_k^{\rm end}$ | (13) |
目标函数归一化线性打分制, 以最大允许温升为60分, 1/20C充电温升为100分. 最大允许温升是电池生产或在使用过程中人为设定的最大温升, 保证电池安全; 1/20C充电温升为最小温升, 因为通常用此倍率测定电池OCV-SOC曲线. 以最大允许充电时间为60分, 极化边界电流充电时间为100分. 最大允许充电时间是用户角度定制的, 因为超过一定长度的充电时间, 用户会焦躁不安难以接受. 最终目标函数为式(14), 采用线性加权的形式, 加权系数
| $\begin{split} (t,\Delta T) = & \alpha \left[ {\frac{{40}}{{{t_{\max }} - {t_{0.05C}}}}(t - {t_{0.05C}}) + 60} \right]\\ &{\beta \left[ {100 + \frac{{40(\Delta T - \Delta {T_{0.05}})}}{{\Delta {T_{0.05}} - \Delta {T_{\max }}}}} \right]} \end{split}$ | (14) |
运行Matlab 遗传算法程序, 设置初始种群数10, 代沟0.9, 代数40, 并设置不同的充电时间和充电温升权重系数, 优化结果如图8~图10所示.
α=0.5, β=0.5优化结果如图8所示.
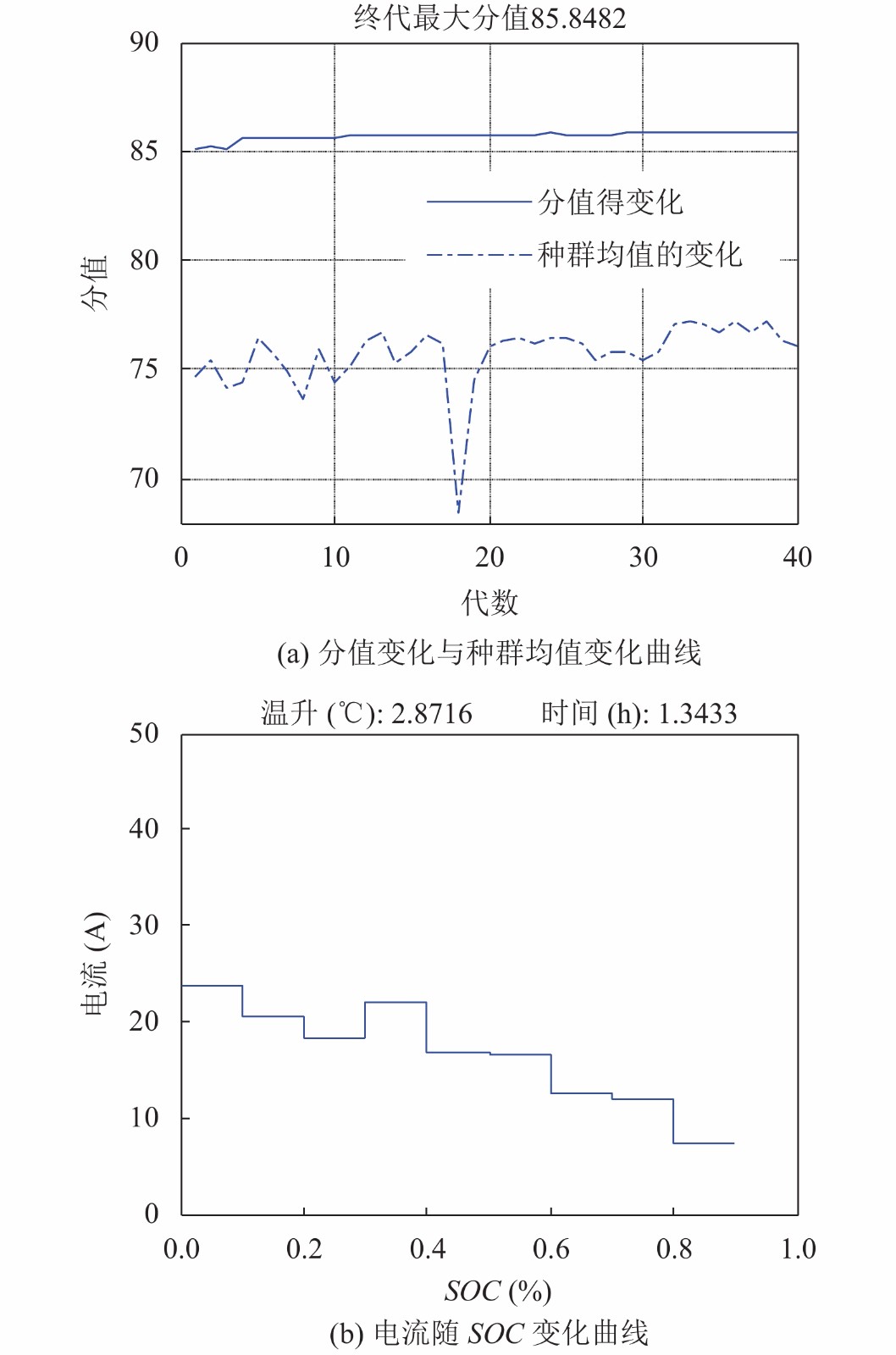
|
图 8 系数α=0.5, β=0.5优化计算结果 |
α=0.3, β=0.7优化结果图9所示.
α=0.7, β=0.3优化结果图10所示.

|
图 9 系数α=0.3, β=0.7优化计算结果 |
从不同权重系数的Matlab仿真优化结果可以看出, 当遗传算法进行40代时, 每代个体的最大适应度值已经近似趋于稳定, 这说明适应度函数即目标函数是收敛的. 由于充电电流以极化电压限制的可接受充电电流为边界条件, 而此电流边界条件随SOC的增加逐渐减小, 所以优化得到的最优充电电流随着SOC的增加整体变化趋势是逐渐减小, 同时, 在某些SOC区间, 充电电流会稍有增加, 这是因为在这些SOC区间, 电池具有较小的内阻或极化, 产热速率相对较低, 因此可以用大电流充电以加快充电速度. 当权重系数α=0.3, β=0.7时, 相应的优化充电电流对应的充电时间为1.99 h, 充电温升为1.9℃; 当权重系数α=0.5, β=0.5时, 相应的优化充电电流对应的充电时间为1.34 h, 充电温升为2.87℃; 当权重系数α=0.7, β=0.3时, 相应的优化充电电流对应的充电时间为1.07 h, 充电温升为3.8℃.

|
图 10 系数α=0.7, β=0.3优化计算结果 |
3 基于充电桩监控平台的充电故障在线预警策略检验
利用充电桩监控平台提供的充电状态信息数据, 对所提出的基于电池模型的充电设施充电数据在线预警进行了验证. 根据电动汽车动力蓄电池的类型、规格以及参数信息构建动力电池模型, 例如电池类型、额定容量、初始荷电状态等信息. 根据提出的模拟动力蓄电池充电响应方法以及电池模型计算模拟动力电池充电响应. 利用CAN总线监听技术, 解析充电过程中充电机和电池管理系统的CAN通信报文, 实时获取充电机和电池充电状态信息以及电池充电需求信息, 将电池模型模拟的充电响应信息与电池的充电状态信息进行对比, 同时将充电机的充电状态信息与电池充电需求信息进行对比, 来判断充电过程是否正常. 如果比对信息的差异在允许范围内则说明充电过程正常, 如果比对信息存在明显差异则说明充电过程有误, 对差异信息进行具体解析, 可以明确充电故障信息, 进而实现充电故障预警.
3.1 正常充电过程选取正常充电过程中的一组完整的电池状态信息数据, 其中包括充电时间、充电电流、充电电压、荷电状态等信息, 在Matlab仿真环境中进行程序设计, 验证所提故障监测方法的可行性. 电池模型的SOC计算数据与BMS提供的SOC数据对比结果如图11所示, 电池模型的计算数据与BMS提供的数据最大相对误差小于2%. 电池模型的电压计算数据与BMS提供的电压数据对比结果如图12所示, 电池模型的计算数据与BMS提供的数据最大相对误差小于0.5%. 以上对比结果说明, 电动汽车充电正常, 充电结果显示电池的初始SOC为60%, 初始电压为552 V, 历时92分钟电池充满, 电压达到570 V.

|
图 11 电池模型的SOC计算数据与BMS提供的SOC数据对比 |

|
图 12 电池模型的电压计算数据与BMS提供的电压数据对比 |
3.2 异常充电过程
选取电动汽车充电事故案例的充电数据进行仿真以验证所提故障监测方法在异常充电过程中的应用. 电池模型的SOC计算数据与BMS提供的SOC数据对比结果如图13所示. 通过图13可以看出, 电池的初始SOC为62%, 在充电历时88分钟电池已经充满的情况下, BMS没有向充电机发送中止充电指令, 电池继续充电, 在正常情况下, 充电过程应停止, 因此说明充电过程出现异常, 应当发出充电故障预警信号. 充电机提供的充电电压信息与BMS提供的充电电压数据对比结果如图14所示, 通过图14可以看出, 当充电历时88分钟电池充满后, 充电过程继续, BMS提供的电池电压数据并没有按照实际充电过程进行更新, 电池充电需求与充电机充电电压存在较大差异, 差异数值超出允许范围, 可以判断由于BMS模块功能失效导致充电过程出现异常或故障, 而充电机由于缺少主动保护机制未及时发出故障预警信号, 没有及时中止充电过程.

|
图 13 电池模型的SOC计算数据与BMS提供的SOC数据对比 |
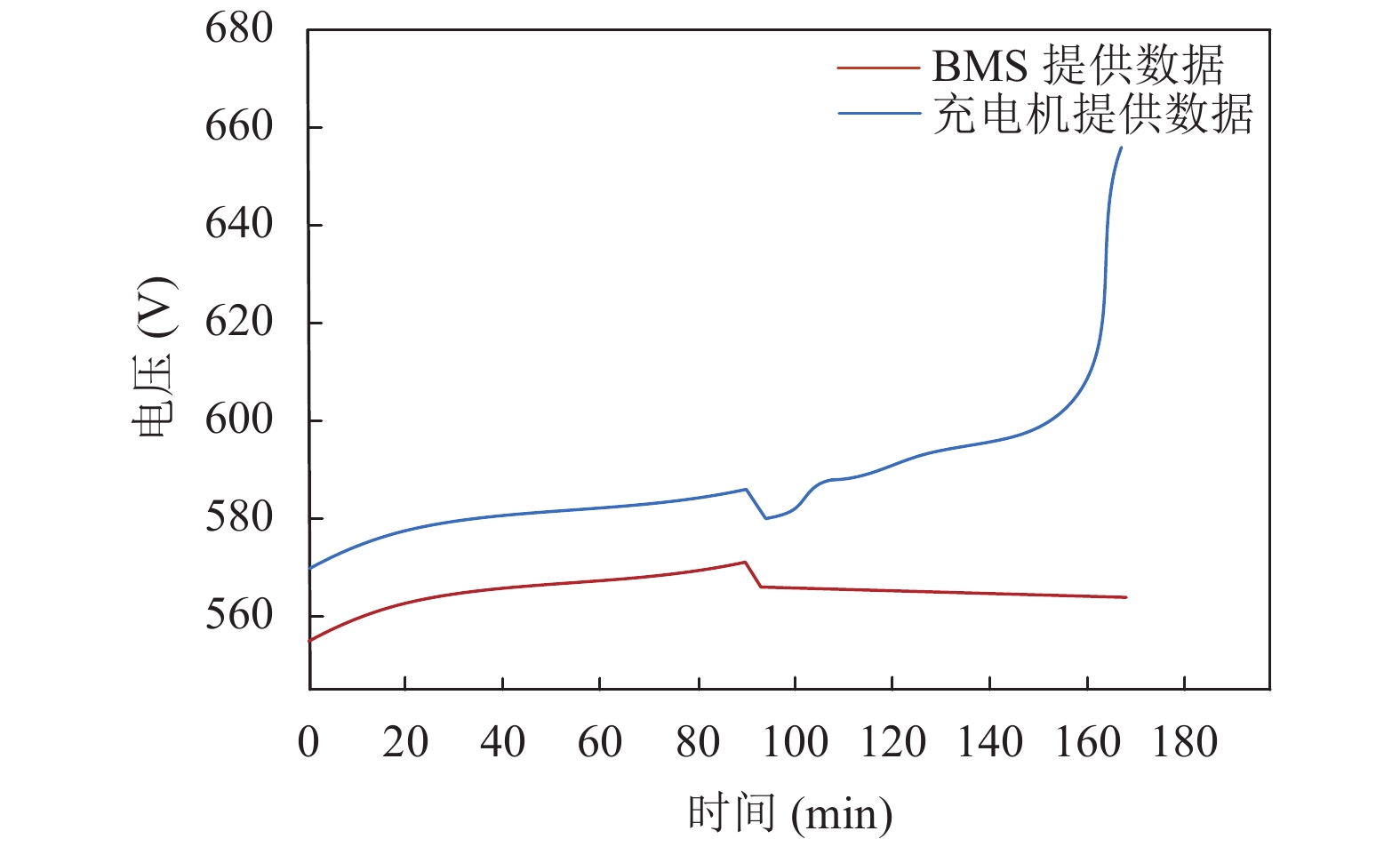
|
图 14 充电机提供电压数据与BMS提供电压数据对比 |
4 结论
本文针对电动汽车充电安全问题, 分析单体电池基本性能, 采用“电压差归一化曲线”来分析动力电池组安全特性, 以短期和中长期不同时间尺度为依据制定安全充电控制策略, 最后利用充电桩监控平台提供的充电状态信息数据, 对所提出的基于电池模型的充电设施充电数据在线预警进行了验证. 本研究能够对电动汽车充电故障进行诊断及预警, 能够最大程度的减少电池在电动汽车运行中出现故障造成的危害, 实现短期与中长期的充电安全智能保护控制功能, 排除隐患.
| [1] |
郭伟伟. 纯电动汽车动力电池故障诊断、维修探究. 湖北农机化, 2020(14): 123-124. DOI:10.3969/j.issn.1009-1440.2020.14.075 |
| [2] |
朱邵杰. 电动汽车充电故障诊断与处理. 农机使用与维修, 2019(5): 49. |
| [3] |
张潇, 栗然, 马涛, 等. 基于主从博弈和贪心策略的含电动汽车主动配电网优化调度. 电力自动化设备, 2020, 40(4): 103-110. |
| [4] |
邱晨曦. 纯电动汽车的故障诊断方法研究. 汽车实用技术, 2019(24): 16-18. |
| [5] |
李雅荣, 巴寅亮, 张雷, 等. 纯电动汽车动力系统故障分析. 汽车实用技术, 2020(2): 188-190, 201. |
| [6] |
张俊. 基于神经网络的纯电动汽车动力电池系统故障诊断. 电子技术与软件工程, 2018(24): 234-235. |
| [7] |
颜乐平, 李琰, 徐天奇. 智能电网中电动汽车充放电实时电价策略研究. 电工技术, 2019(24): 177-180. |
| [8] |
张锋, 张金, 高安同, 等. 基于模型的锂离子电池健康状态预测. 电子技术应用, 2014, 40(12): 79-81, 85. DOI:10.3969/j.issn.0258-7998.2014.12.033 |
| [9] |
侯瑞磊, 范秋华. 基于卷积自编码神经网络的锂离子电池健康状况评估方法研究. 计算机测量与控制, 2020, 28(8): 265-269, 275. |
| [10] |
林群, 赵璞, 段浩. 考虑电动汽车充放电功率不确定性的主动配电网鲁棒调度. 能源与环境, 2019(6): 59-61. DOI:10.3969/j.issn.1672-9064.2019.06.027 |
 2021, Vol. 30
2021, Vol. 30



