登机口分配问题求解的目标函数通常考虑两个主要目标: 最小化登机口的使用数量和最小化所有航班的延误时间[1,2]. 在与登机口相关的约束条件当中, 例如登机口只能容纳特定类型的飞机、两个大型飞机不能同时被分配到两个登机口等, 这些条件必须进行考虑[3,4]. 当飞机的数量比较少时, 可以通过变换不同的目标条件来生成有效的分配计划. 但是当飞机数量的显著增加时, 我们就很难生成有效的分配方案[5]. 在目前国内外的研究中, 有关登机口分配问题的求解方法可以分为两类: (1)精确算法, 其能够产生最优的解决方案. 比较典型的有: Mangoubi等[6]提出了整数线性规划模型, 并以最小化旅客的行走距离为目标. Bihr[7]提出了一种原始对偶单纯形算法, 并找到了最优解. Yan等[8]建立了多目标0-1整数规划模型, 并使用加权方法、列生成方法、单纯形法和分支定界法来求解该模型. 李云鹏等[9]使用CPLEX求解混合整数规划模型. Bolat[10], Xu等[11]和Li[12]使用分支定界法来求解他们建立的模型. 但是由于登机口分配问题是一个NP-hard的组合优化问题, 当扩大求解规模后, 可行解的数量将呈指数增加, 如果仍然采用精确算法来求解的话, 会导致维数灾难, 因此研究学者们提出了启发式算法和元启发式算法来对该问题进行求解. (2)启发式算法和元启发式算法. Xu等[11]采用禁忌搜索算法对登机口分配的0-1混合整数二次规划模型进行求解, 该模型以旅客步行总时间为目标函数, 并没有考虑捷运时间和流程时间, 而且禁忌搜索算法对初始解的依赖性较强. Ding等[13]对过量限制条件下的登机口分配问题进行了研究, 并对文献[11]中提出的禁忌搜索方法进行了改进, 同时提出了禁忌搜索混合模拟退火和模拟退火算法, 但是他们只考虑了最小化航班数和旅客的行走总距离, 并未考虑时间因素. Lim等[14]考虑了航班到达和离开时间可能发生变化的更现实的情况, 并使用“插入移动算法”, “间隔交换移动算法”和“贪婪算法”, 以解决建立的登机口分配模型, 和本文相比, 没有考虑最小化登机口的数量. 陈欣等[15]设计了一种排序模拟退火算法以求解枢纽机场的停机位指派问题, 同样没有考虑最小化登机口的数量. 鞠姝妹等[16]以旅客满意度为优化目标建立数学模型, 并设计了贪婪模拟退火算法来求解枢纽机场的停机位分配问题, 该学者只是从顾客的角度来建立模型, 并没有考虑机场的登机口使用情况. Zhao等[17]建立了一种混合整数模型, 并设计了蚁群算法对该模型进行求解, 与本文不同的是, 该文并未考虑登机口情况, 而且蚁群算法一般需要较长的搜索时间. Dell’Orco等[18]基于模糊蜂群优化(FBCO)开发了一种新的元启发式算法, 该算法将BCO的概念与模糊推理系统相结合, 该文在建模方面和本文比较相似, 都考虑了旅客和机场登机口两个方面, 但是本文的考虑更加全面. Yu等[19]扩展了传统的登机口分配问题, 同时考虑了传统成本和鲁棒性, 并建立了数学模型, 然后设计了自适应大邻域搜索(ALNS)算法来求解该模型, 与其不同的是, 本文重点考虑的是时间和登机口两个因素. Wu等[20]设计了基于蚁群协同策略和信息素更新策略的改进蚁群优化算法(ICQACO)来解决他们提出的多目标优化模型, 与该文不同的是, 本文考虑了最小化登机口数量.
综上所述, 针对登机口分配问题, 本文综合考虑时间和登机口使用数量两个方面来建立数学模型, 并结合变邻域搜索的邻域构造思想, 综合利用集束搜索和模拟退火算法的优势, 提出了一种优化效果和鲁棒性均较好的求解算法——基于集束搜索的改进型模拟退火算法, 通过算例验证了该算法的优化效果和鲁棒性.
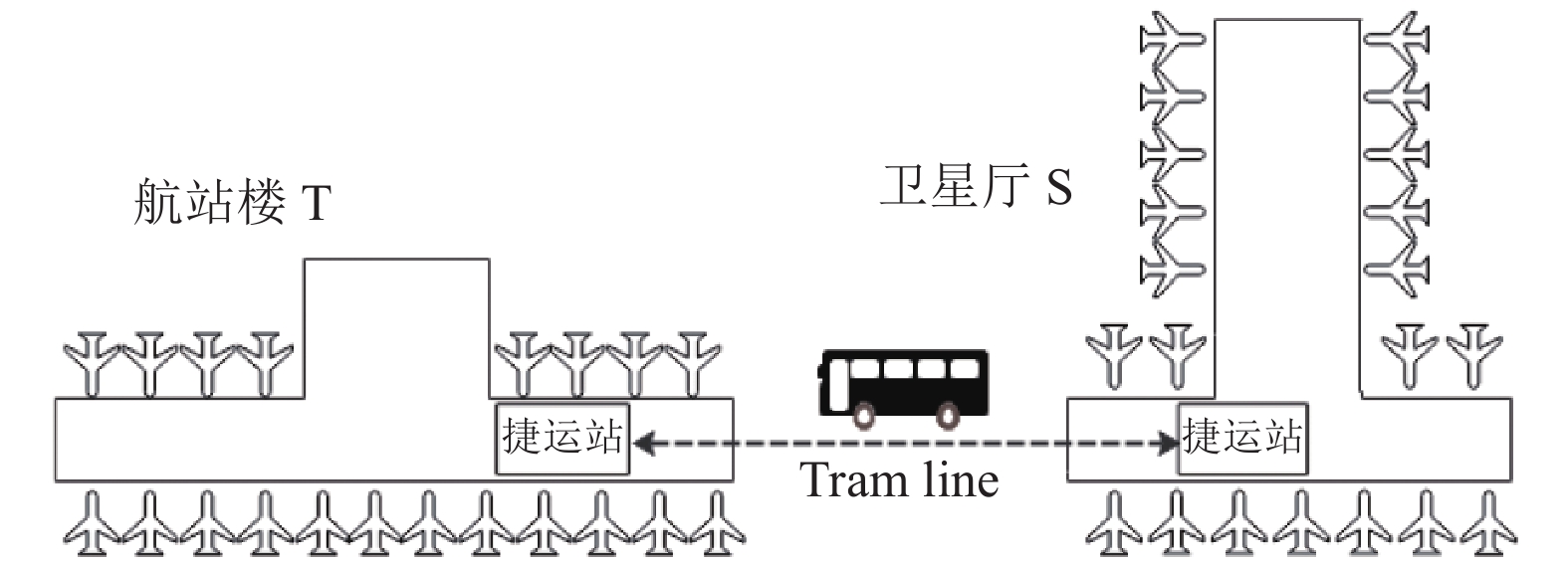
1 问题描述本文以某机场固定登机口分配为研究对象, 并假定该机场现有航站楼T的旅客流量已达饱和状态, 为了应对未来的发展, 现正增设卫星厅S. 其中航站楼T的所有登机口集合为K, 卫星厅S中的临时登机口数量假设为无限, 示意图如图1所示.
|
图 1 卫星厅S相对于航站楼T示意图 |
(1)机场布局: 该机场包含了航站楼T和卫星厅S; 航站楼T具有完备的国际机场航站楼所拥有的功能, 其中包含出发、到达、出入境及候机功能. 而卫星厅S为航站楼T延伸, 但其功能只有候机, 没有设置出入境的功能. 同时航站楼T与卫星楼S之间具有相通的快速运输通道, 称为捷运通道, 能够快速的运送国内及国际的出入境旅客. 现假设旅客无需等待, 随时可以离开, 并且单程运送旅客所需的时间为8分钟.
(2)登机口的分配: 登机口是用来在飞机停靠时, 对飞机进行相关技术操作的固定位置, 一般每个登机口统一配备专业的设备. 分配航班的登机口需要考虑以下几个规则: 其一, 航站楼T和卫星楼S的所有登机口规划统筹和分配; 其二, 考虑到每个登机口的国内/国际, 到达/离开, 宽体机型/窄体机型等的功能. 飞机转场计划中的航班需分配给与其属性匹配的登机口; 其三, 每次飞机转机的出发和到达航班必须分配在同一登机口, 不能转移到其他登机口; 其四, 分配于同一登机口的两架飞机之间的空档时间间隔必须大于或等于45分钟; 最后, 机场存在临时停机位, 当出现无法分配固定登机口时飞机可以停靠, 国内和国际飞机均可以停靠在临时停机位.
(3)旅客流程: 旅客可以分为以3类, 包括始发旅客、终点到达旅客、过境中转旅客. 由于新建立的卫星大厅对始发旅客和终点到达旅客的影响较小, 所以这两类旅客不属于本文所研究的对象. 而过境中转旅客则可以根据前一航班到达至后一航班出发之间的流程, 按国内航班(D)和国际航班(I), 航站楼(T)和卫星大厅(S)组成16种不同的场景. 同时最短流程时间不包括捷运通行时间和旅客步行时间.
(4)旅客换乘紧张度: 表示旅客航班换乘时间除以航班的连续时间, 而航班的换乘时间则等于最短旅客流程时间加上捷运通行时间以及步行时间. 航班的连续时间等于前一航班的达到时间减去下一航班的出发时间.
本文在航班合理分配登机口的基础上, 尽可能的减少登机口数量和临时登机口的使用数量, 同时还需考虑旅客换乘影响因素, 例如旅客的捷运时间、行走时间及航班连接时间, 这3个外生变量. 而新建的卫星厅则延长了中转旅客的换乘时间, 本文综合考虑了所有旅客的换乘紧张度、使用登机口的数量、使用临时登机口的数量, 使其加权和最小.
2 数学模型建立 2.1 基本假设假设临时机位的数量无限多, 停留在临时登机口飞机的乘客不计算其换乘紧张度. 因为在模型中已最小使用临时登机口的数目, 假设临时机位数量无限多, 为了防止飞机无法安排在合适的登机口, 得不到可行解.
2.2 参数及决策变量的定义(1)参数
(2)决策变量
| $M(c) = \frac{{\displaystyle\sum\limits_{k \in K} {\displaystyle\sum\limits_{m \in K} {\displaystyle\sum\limits_{p \in L} {\displaystyle\sum\limits_{q \in L} {\left( {t_{kpmq}^c + d_{kpmq}^c + g_{km}^c} \right) \cdot y_{kpmq}^c} } } } }}{{{e_c} - {s_c}}},\;\;c \in C$ |
| $N(c) = \frac{{360 + \displaystyle\sum\limits_{k \in K} {\displaystyle\sum\limits_{m \in K} {\displaystyle\sum\limits_{p \in L} {\displaystyle\sum\limits_{q \in L} {d_{kpmq}^c + g_{km}^c} } } } }}{{{e_c} - {s_c}}},\;\;c \in C$ |
建立的0-1整数线性规划模型为:
| $ \begin{split} & \min {w_1}\sum\limits_{i \in I} {{{\text{z}}_i}} + {w_2}\left( {\sum\limits_{c \in C\backslash \left\{ {c|f = 1} \right\}} {M(c) + \sum\limits_{c \in C} {{f_c} \cdot N(c)} } } \right) \\ & + {w_3}\sum\limits_{k \in K} {{u_k}} \;\; \\ \end{split} $ | (1) |
s.t.
| $ {x} \le {d},\;\;k \in K,\;\;i \in I $ | (2) |
| $ \sum\limits_{i \in I} {{x_{ik}}} \le M \cdot {u_k},\;\;k \in K $ | (3) |
| $ \sum\limits_{k \in K} {{x_{ik}}} + {{\text{z}}_i} = 1,\;\;i \in I $ | (4) |
| $ {s_j} + M \cdot (1 - {l_{ij}}{\rm{)}} \ge {e_i}{\rm{ + }}\tau, \;\;i \ne j,\;\;i,j \in I $ | (5) |
| $ {l_{ij}}{\rm{ + }}{l_{ji}} \ge {x_{ik}}{\rm{ + }}{x_{jk}}{\rm{ - 1 }},\;i \ne j,\;\;j \in I,\;\;k \in K\;\; $ | (6) |
| $\left\{ \begin{gathered} {s_c}{\rm{ + }}t_{kpmq}^c \cdot y_{kpmq}^c - {f_c} \cdot M \le {e_c} \\ {\rm{s.t.}}\;c \in C,\;\;k,m \in M,\;\;p,q \in L \\ \end{gathered} \right. $ | (7) |
| $\left\{ \begin{split} & y_{kpmq}^c \cdot {h_{ci}} \le {x_{ik}}\\ &{\rm{ s.t.}}\;\; c \in C,\;\;k,m \in M,\;\; p,q \in L,\;i \in I \\ \end{split} \right. $ | (8) |
| $\left\{ \begin{split} & y_{kpmq}^c \cdot {h_{cj}} \le {x_{jm}}\\ & {\rm{s.t.}}\;c \in C,\;\;k,m \in M,\;\; p,q \in L,\;\;j \in I \\ \end{split} \right. $ | (9) |
| $ {x_{ik}},y_{kpmq}^c,{u_k},{{\text{z}}_i},{l_{ij}} \in \left\{ {0,1} \right\} $ | (10) |
其中, 在目标函数式(1)中, 第一项为临时机位的数量, 第二项为中转旅客的换乘紧张度, 第三项为被使用登机口的数量; 约束条件式(2)表示停靠飞机的类型必须和登机口允许的类型一致; 约束条件式(3)表示如果有飞机停在某登机口, 则表明该登机口被使用; 约束条件式(4)表示每架飞机都至少要停在固定登机口或者临时机位; 约束条件式(5)表示停靠在同一个登机口的两架飞机, 后一飞机必须在前一飞机起飞后
模拟退火算法(simulated annealing algorithm)是一种根据给定的函数, 通过概率选择构造解获得全局近似最优解的启发式算法. 该算法的优点是在初期就能够搜索广泛的解空间, 并能通过扩大搜索范围以及接受较差解来避免算法陷入局部最优, 最早由Kirkpatrick用以解决组合优化问题, 但在后来的大量研究发现, 传统的模拟退火算法在面临大规模的优化问题时, 普遍存在算法参数敏感、易早熟陷入局部最优等问题.
3.2 集束搜索改进模拟退火算法集束搜索(beam search)是一种根据给定的规则, 通过下界来指导搜索过程的经典搜索树算法, 在不排除最优解的期望下, 减掉一些质量较差的解, 保留质量较高的解, 提高整体算法性能. 改进后的算法的基本框架同模拟退火算法相同, 但是在迭代规则构造方法上采用集束搜索, 同时利用了Two-exchange算子及Relocate算子构造领域, 通过保留一定数量的不完全解及增加搜索空间, 来避免算法陷入局部最优解, 弥补传统模拟退火算法的不足.
基于此, 本文结合变邻域搜索的邻域构造思想, 综合利用集束搜索和模拟退火算法的优点, 提出了基于集束搜索的改进型模拟退火算法(simulated annealing algorithm based beam search), 并使用该方法对本文模型进行求解.
第1步: 参数初始化
(1) 给出初始解: 加权的使用临时登机口的数目, 使用登机口的数目, 和在固定登机口的旅客数目之和最小为目标函数, 以式(2)~式(6)为约束, 用CPLEX求出该问题的最优解作为初始解, 这个初始解只考虑了飞机-登机口分配, 分配好之后, 乘客与飞机绑定在一起, 这样只是构造一个初始解.
(2) 设定初始温度为
第2步: 基于Two-exchange算子的邻域构造
Two-exchange算子: 交换两个登机口所停靠的飞机, 令在登机口
利用Two-exchange算子得到上述解的集合中每个解的领域, 在其中按照如下模拟退火规则选取n个较优的子代解:
(1) 如果子代解的目标值优于父代解, 则保留;
(2) 如果子代解的目标值与父代解相同, 则以一定的小概率p保留;
(3) 如果子代解的目标值劣于父代解, 则根据:
| $p = 1 - {e^{ - \textstyle\frac{\Delta }{T}}}$ |
其中,
决策保留的子代解, 越差的解保留概率越大;
(4)如果保留的解集个数已经达到了上限n, 则遍历已保留的解, 替换第一个找到比当前保留的解大的解; 如果是未改进的解, 则不保留.
第3步: 基于Relocate算子的邻域构造
Relocate算子: 将停靠在某个登机口的飞机转移到另一个登机口去停靠, 对停靠在登机口
利用Relocate算子得到上述解的集合中每个解的领域, 与上述模拟退火规则相同选取n个较优的子代解.
第4步: 基于集束搜索的迭代规则构造
将上述两个集合合并, 若其中有优于全局最优解的则进行更新, 否则从合并后的集合中根据下列集束搜索规则选取
(1)首先将该集合按照目标值由小到大进行排序;
(2)选取
(3)更新当前温度
第5步: 终止条件
判断循环条件并执行循环, 如果当前温度
(1)保留概率计算方式的改进.
原始模拟退火算法的保留概率计算方式为:
| $p = {e^{ - \textstyle\frac{\Delta }{T}}}$ |
本文提出算法的保留概率计算方式正好与此相反, 这样做是为了增强解的跳跃能力, 所以越差的解保留概率越大.
(2)利用变邻域搜索算法的优势, 同时使用算子.
同时使用两种算子, 扩大产生的邻域范围, 同时如果保留的解集个数已经达到了上限
(3)允许较优解和较劣解同时进入下一次迭代.
集束搜索一般会选择目标值更优的多个解进入下一次迭代的考虑, 考虑选择较优解和较劣解进入下一次迭代的优势在于有助于避免陷入局部最优解, 从而有助于逼近最优解.
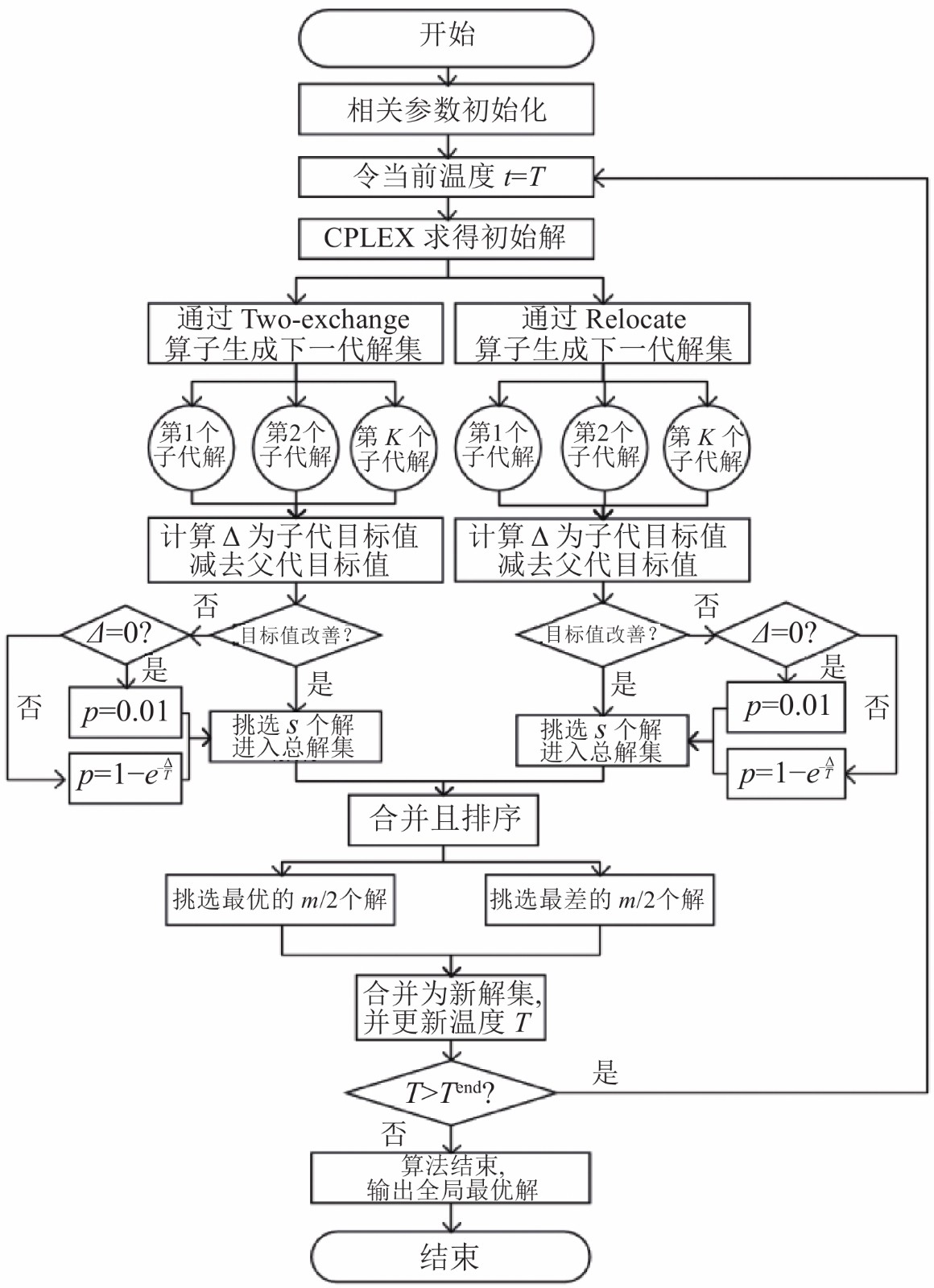
|
图 2 改进模拟退火算法流程图 |
4 算例分析
数据来源包含某月20号的某机场的飞机转场记录和旅客中转记录数据以及通过计算机随机生成的旅客数据. 其中航站楼T有28个登机口, 航站楼S有41个登机口, 飞机共计305架. 在建立数学模型时, 包含临时机位数目权重
本文所考虑的基准算法是禁忌搜索(Tabu Search)、变邻域搜索(Variable Neighborhood Search), 并加入经典蚁群算法(Ant Colony Algorithm)进行求解性能对比, 通过对这些参数进行调整, 得到各种乘客下的4种算法的最优求解结果, 如表1所示.
| 表 1 不同乘客数下3个算法性能对比 |
从表1中可以看出, 在不同的乘客数下, 随着乘客数的增加, 本文所提出算法的优化效果都是要优于禁忌搜索算法、变邻域搜索算法和经典蚁群算法. 而且从表中改进百分比数据可以看出, 相较于3个算法的最优结果, 本文所提出算法的优化改进效果基本上都在5%以上, 由此可见本文算法的优化效果非常明显.
5 结论本文研究了新建卫星厅S对中转旅客的航班衔接的影响, 为了优化登机口分配和降低中转旅客的换乘紧张程度, 建立了0-1整数规划模型, 利用本文所提出的基于集束搜索的改进模拟退火算法对问题进行求解, 解结果表明: 与禁忌搜索算法、变邻域搜索算法和经典蚁群算法相比, 本文所提出算法的优化效果更好. 从实际应用的角度来说, 本文所提出模型对航班-登机口的分配问题具有重要参考价值, 对提高机场的运营能力和旅客的服务水平大有裨益, 本文所提出算法对于未来登机口问题的求解具有重大的参考和应用价值.
| [1] |
Steuart GN. Gate position requirements at metropolitan airports. Transportation Science, 1974, 8(2): 169-189. DOI:10.1287/trsc.8.2.169 |
| [2] |
Bouras A, Ghaleb MA, Suryahatmaja US, et al. The airport gate assignment problem: A survey. The Scientific World Journal, 2014, 2014: 923859. DOI:10.1155/2014/923859 |
| [3] |
Maharjan B, Matis TI. Multi-commodity flow network model of the flight gate assignment problem. Computers & Industrial Engineering, 2012, 63(4): 1135-1144. |
| [4] |
Castaing J, Mukherjee I, Cohn A, et al. Reducing airport gate blockage in passenger aviation: Models and analysis. Computers & Operations Research, 2016, 65: 189-199. DOI:10.1016/j.cor.2014.02.011 |
| [5] |
Dorndorf U, Jaehn F, Pesch E. Flight gate assignment and recovery strategies with stochastic arrival and departure times. OR Spectrum, 2017, 39(1): 65-93. DOI:10.1007/s00291-016-0443-1 |
| [6] |
Mangoubi RS, Mathaisel DFX. Optimizing gate assignments at airport terminals. Transportation Science, 1985, 19(2): 173-188. DOI:10.1287/trsc.19.2.173 |
| [7] |
Bihr RA. A conceptual solution to the aircraft gate assignment problem using 0, 1 linear programming. Computers & Industrial Engineering, 1990, 19(1–4): 280-284. DOI:10.1016/0360-8352(90)90122-3 |
| [8] |
Yan SY, Huo CM. Optimization of multiple objective gate assignments. Transportation Research Part A: Policy and Practice, 2001, 35(5): 413-432. DOI:10.1016/S0965-8564(99)00065-8 |
| [9] |
李云鹏, 张则强, 管超, 等. 停机位分配问题的整数规划模型及启发式求解方法. 系统工程, 2020, 38(1): 103-112. |
| [10] |
Bolat A. Procedures for providing robust gate assignments for arriving aircrafts. European Journal of Operational Research, 2000, 120(1): 63-80. DOI:10.1016/S0377-2217(98)00375-0 |
| [11] |
Xu JF, Bailey G. The airport gate assignment problem: Mathematical model and a tabu search algorithm. Proceedings of the 34th Annual Hawaii International Conference on System Sciences. Maui, HI, USA. 2001. 102–111.
|
| [12] |
Wang L. Optimized assignment of civil airport gate. Proceedings of 2010 International Conference on Intelligent System Design and Engineering Application. Changsha, China. 2010. 33–38.
|
| [13] |
Ding H, Lim A, Rodrigues B, et al. The over-constrained airport gate assignment problem. Computers & Operations Research, 2005, 32(7): 1867-1880. |
| [14] |
Lim A, Rodrigues B, Zhu Y. Airport gate scheduling with time windows. Artificial Intelligence Review, 2005, 24(1): 5-31. DOI:10.1007/s10462-004-7190-4 |
| [15] |
陈欣, 陆迅, 朱金福. 停机位指派模型的排序模拟退火算法. 应用科学学报, 2007, 25(5): 520-525. DOI:10.3969/j.issn.0255-8297.2007.05.016 |
| [16] |
鞠姝妹, 许俐. 基于GSAA的停机位指派优化问题的研究. 交通运输系统工程与信息, 2008, 8(1): 138-143. DOI:10.3969/j.issn.1009-6744.2008.01.024 |
| [17] |
Zhao H, Cheng LQ. Ant colony algorithm and simulation for robust airport gate assignment. Mathematical Problems in Engineering, 2014, 2014: 804310. |
| [18] |
Dell’Orco M, Marinelli M, Altieri MG. Solving the gate assignment problem through the Fuzzy Bee Colony Optimization. Transportation Research Part C Emerging Technologies, 2017, 80(1): 424-438. |
| [19] |
Yu CH, Zhang D, Lau HYK. An adaptive large neighborhood search heuristic for solving a robust gate assignment problem. Expert Systems with Applications, 2017, 84: 143-154. DOI:10.1016/j.eswa.2017.04.050 |
| [20] |
Wu D, Sun M, Zhao HM, et al. Study on an airport gate assignment method based on improved ACO algorithm. Kybernetes, 2018, 47(1): 20-43. DOI:10.1108/K-08-2017-0279 |
 2021, Vol. 30
2021, Vol. 30



