2. 太原科技大学 经济与管理学院, 太原030024
2. School of Economics and Management, Taiyuan University of Science of Technology, Taiyuan 030024, China
课程是人才培养的核心要素. 教育部部署进行的高校“金课”建设, 即一流课程建设, 事关一流专业这个人才培养基本单元的建设成效和一流本科教育的成败[1]. 课程评价是课程建设的有力抓手, 评价结果可用来指导课程建设方向和课程改革实践. 为此, 教育部制定了包括教学队伍、教学内容、教学资源等维度的课程评价指标体系[2]. 洞悉评价指标间关系, 可为高校的教育管理决策提供有效支撑. 数据驱动的管理与决策, 是传统的模型驱动或流程驱动决策范式的有益补充和拓展[3]. 数据分析和数据挖掘, 则为数据驱动的管理决策提供了技术支持. 通过挖掘课程评价数据, 能够提取有价值的知识, 为课程管理决策提供依据.
评价指标体系直接关系课程评价结果. 2010年, 国家精品课程评审指标(本科)制定, 体现了《教育部财政部关于实施高等学校本科教学质量与教学改革工程的意见》(教高[2007] 1号)、《教育部关于进一步深化本科教学改革全面提高教学质量的若干意见》(教高[2007] 2号)和《教育部关于启动高等学校教学质量与教学改革工程精品课程建设工作的通知》(教高[2003] 1号)等文件精神[4]. 某高校也结合自身实际, 制定了涵盖教学队伍、教学内容、教学资源等维度的精品课程评价指标体系, 设置了包括教师风范、教学水平、教研活动及成果、教师知识结构、年龄结构的观测点.
课程评价的目的, 在于辅助教学管理决策, 指导课程建设. 鉴于评价指标间存在关联关系, 故可用关联规则挖掘算法来提取关联规则. 任高举等[5]通过视图对Apriori算法的频繁项集产生进行了改进, 使用改进的Apriori算法挖掘教学评价数据, 发现学历、职称和教龄等影响课程质量, 但仅考虑教师对课程的影响, 分析因素比较单一. 郭鹏等[6]通过加入兴趣度的方式对Apriori算法产生的强规则进行了过滤, 使用改进的Apriori算法对不同课程的成绩进行挖掘分析, 发现不同课程成绩之间存在关联关系. 以上工作, 从单一角度对课程教学数据进行关联规则的挖掘分析, 对于课程建设的指导作用有限. 为此, 选取某校本科生课程作为研究对象, 提出一种基于差异兴趣度的Apriori算法, 对课程评价指标进行多维度的关联规则提取, 期望提升教学管理的科学化水平.
2 基于兴趣度的Apriori关联规则挖掘算法传统的Apriori算法, 是一种挖掘布尔关联规则频繁项集的算法, 建立在先验原理的广泛优先搜索基础上[7]. 为进行关联规则筛选, 提出了支持度和置信度两个概念.
(1)关联规则
关联规则, 是描述事务的某些属性与其他事务的若干属性同时出现的规则和模式[8]. 对于课程评价, 关联规则可描述如下: 设数据集合
关联规则的强度用支持度和置信度衡量[9]. 支持度指事务数据集D中包含项集X和Y的事务个数占总数的比例, 记为
| $Support(X \Rightarrow Y) = P(XY) = \frac{{number(XY)}}{{number(D)}}$ | (1) |
| $Confidence(X \Rightarrow Y) = P(Y|X) = \frac{{S\!upport(X \Rightarrow Y)}}{{S\!upport(X)}}$ | (2) |
要确定一条规则为强关联规则, 须看其是否同时满足最小支持度和最小置信度阈值条件. 最小支持度用来测量项集在统计中出现的最小频率, 记为
(2)兴趣度
传统Apriori算法, 仅使用支持度和置信度阈值来提取关联规则, 结果可能并非均属有趣, 甚至可能引起误解[10]. 其原因是, 支持度缺陷会导致部分有意义的规则由于支持度小而遭忽略; 置信度的缺陷, 则由于忽视了规则后件项集在事务中的支持度导致非有趣结果的产生. 如式(3)所示, 文献[11]引入差异兴趣度进行规则的有趣性判断, 进而对频繁项集进行筛选.
| $Interest(X \Rightarrow Y) = \frac{{P(Y|X) - P(Y)}}{{\max \left\{ {P(Y|X),P(Y)} \right\}}}$ | (3) |
这里, 兴趣度
(3) 基于兴趣度的Apriori算法
频繁项集筛选的目的, 在于抑制误导性关联规则的生成. 基于差异兴趣度的频繁项集筛选, 以及改进的Apriori算法流程见算法1.
算法1. 改进的Apriori算法
输入: 数据集D, 最小支持度, 最小置信度, 最小兴趣度
过程:
1)扫描全部数据D, 产生候选频繁1-项集的集合
2)根据最小支持度, 由候选1-项集的集合
3)对
4)由
5)根据最小支持度, 由候选
6)若
7)根据最小置信度和兴趣度, 由频繁项集产生强关联规则, 结束.
输出: 符合条件的规则.
3 挖掘过程及结果分析 3.1 数据采集用于分析的420条数据, 来自某校10门本科生课程的问卷调查, 面向学生、教师、同行专家和教学督导组等4类人群, 经由课程评价指标设计的课程评价问卷调查系统采集, 课程评价部分指标见表1, 其中每个二级指标评分可取A、B、C、D、E五个等级中的一个, 数据结构见表2. 经过集成, 每条记录包括教学队伍、教学内容、教学资源、教学方法与手段等4个维度的12个属性. 部分原始数据见表3.
3.2 数据预处理为了提高数据挖掘结果的准确性, 需要对原始数据进行预处理. 数据预处理主要包括数据清洗和数据变换等环节.
| 表 1 课程评价指标 |
| 表 2 数据结构 |
(1)数据清洗
通过问卷调查系统采集的原始数据中, 由于人为因素存在极端现象, 譬如全部好评或差评, 对这部分数据做了删除处理. 由于问卷调查系统采集数据时存在系统或者人为因素影响, 有部分指标的采集结果缺失, 对于缺失的数据项, 受数据集的限制, 不宜进行删除, 经分析之后, 发现其中某选项出现的频率在50%以上, 为此我们采用众数的填补方法. 因为出现频率最高的选项, 比例已经超过一半, 所以使用众数对部分空白的填补并不会影响整个数据的分析. 经过数据清理, 记录数为412, 占样本数据的98.1%.
| 表 3 部分原始数据 |
(2)数据转换
Apriori算法主要适用于单维属性值数据, 换言之, 数据的属性值都可以看成A是否存在的简单形式[10]. 但在现实中, 数据常是多维的, 意味着无法直接使用Apriori算法来挖掘关联规则. 根据国家精品课程的评审及教育教学的改革要求, 设计的一级评价指标教学队伍、教学内容教学条件等, 为了更加全面的表述一级指标, 需要在一级指标下设计二级指标, 包含课程负责人与主讲、教学队伍结构及整体素质、教学改革与研究等. 而根据课程评价指标采集到的数据涉及到多个维度, 无法直接使用Apriori算法进行分析.
针对上述问题, 提出一个解决办法. 其思想是, 用3位十进制数表征课程评价数据的属性, 其中, 第一位数表示一级指标, 分别取1, 2, …; 第二位数表示二级指标, 根据观测点的实际设置情况, 分别取1, 2, …; 第三位数, 按照采样数据等级A/B/C/D/E, 分别表示为1/2/3/4/5, 见图1.

|
图 1 数据转换规则 |
依据转换规则构造完成数据集. 譬如, 将“一级指标=‘1 教学队伍’”“二级指标=‘1-1 课程负责人与主讲教师’”, 与“课程主要观测点=‘教师风范、学术水平与教学水平’”对应的“等级=‘B’”评价数据, 转换表征为112. 转换后的部分数据见表4.
| 表 4 部分数据转化结果 |
3.3 实验环境
实验环境为i5-6300HQ(2.3 GHz)CPU、16 GB内存和Microsoft Windows 10专业版操作系统. 在JetbrainsPyCharm2019.3集成开发环境下, 使用Python3.6作为编程语言, anaconda作为解释器.
3.4 规则提取与分析分别使用传统Apriori算法、基于文献[11]概率兴趣度的Apriori算法和本文采用的基于差异兴趣度的Apriori算法, 对形如表3的转换后课程评价数据进行关联规则挖掘, 并分析结果.
(1)误导抑制效果分析
经过多次重复实验, 设定最小支持度Smin=0.2, 最小置信度Cmin=0.45, 最小兴趣度Imin=0.5. 此时, 使用传统Apriori算法可获取25条关联规则. 这些关联规则中, 很多系无意义或误导性的, 部分误导性规则见表5. 引入兴趣度后只能提取18条关联规则.
| 表 5 提取的部分无意义或误导性关联规则 |
以表5中的规则1为例. 现实世界中, 指标项“网络教学资源”与“教学队伍结构及整体素质”之间存在内在关联的支持度并不高, 很难揭示资源类和人员类事务间的逻辑蕴含关系. 但规则1却显示, 网络教学资源获评“优”时, 教学队伍结构及整体素质将以较大概率获评“中”, 显得牵强. 类似地, 规则2显示, 条件类事务与人员类事务间存在关联关系, 也很难成立.
进一步地, 分别改变参数设置(最小置信度
图2至图4显示, 在支持度、置信度、兴趣度等参数组合的各自设定范围内, 提取的规则数量分别随支持度、置信度、兴趣度的增大而减少.
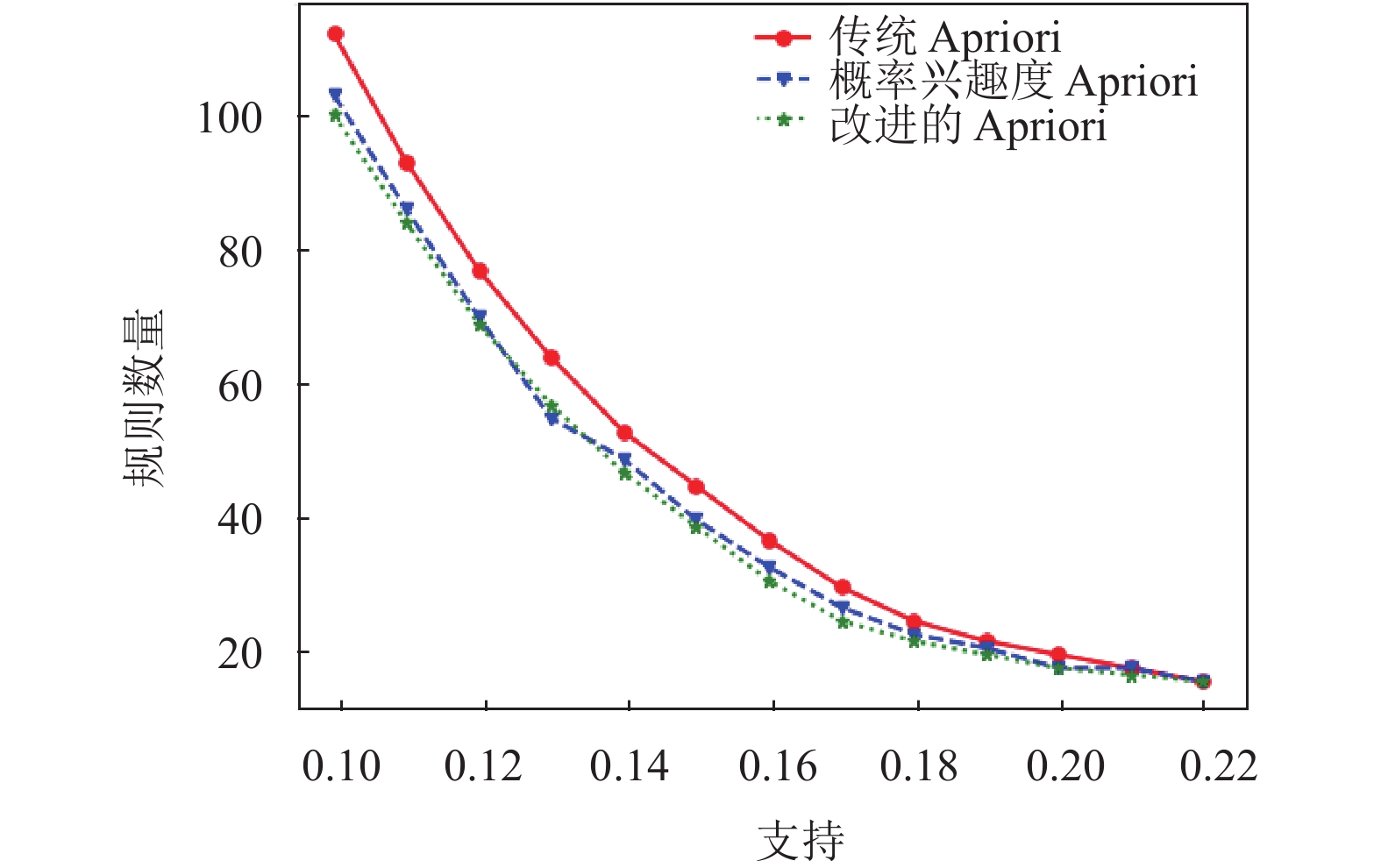
|
图 2 不同支持度下3种算法提取规则数量比较(Cmin=0.3, Imin=0.5) |
图2在设定置信度和兴趣度参数的前提下, 随着支持度增大, 使用改进的Apriori算法提取的规则数量开始时较使用传统算法减少较多, 最后逐渐接近, 而改进的Apriori算法提取的规则数量较概率兴趣度的Apriori算法虽然有部分较多, 但整体趋势还是少于概率兴趣度的Apriori算法, 表明加入兴趣度的Apriori算法可减少误导性规则产生, 改进的Apriori算法更能减少误导性规则的产生.

|
图 3 不同置信度下3种算法提取规则数量比较(Smin=0.2, Imin= 0.5) |
图3在设定支持度和兴趣度参数的前提下, 随着置信度增大, 使用改进的Apriori算法产生的规则数量开始时较使用传统Apriori算法少许多, 最后逐渐接近, 而改进的Apriori算法产生的规则数量整体趋势少于概率兴趣度Apriori算法, 表明引入兴趣度之后可减少误导性规则生成的数量, 改进的Apriori算法更能减少误导性规则的产生.
图4在设定支持度和置信度参数, 且在Apriori算法中引入兴趣度的前提下, 随着兴趣度增大, 概率兴趣度Apriori算法以及改进的Apriori算法提取的规则数量逐渐变少, 从整体趋势观察, 改进的Apriori算法产生的规则数量要少于概率兴趣度Apriori算法. 与之相比, 使用传统Apriori算法进行挖掘, 提取的规则数量没有变化, 表明引入兴趣度可减少误导性规则的产生, 改进的Apriori算法更能减少误导性规则的产生.
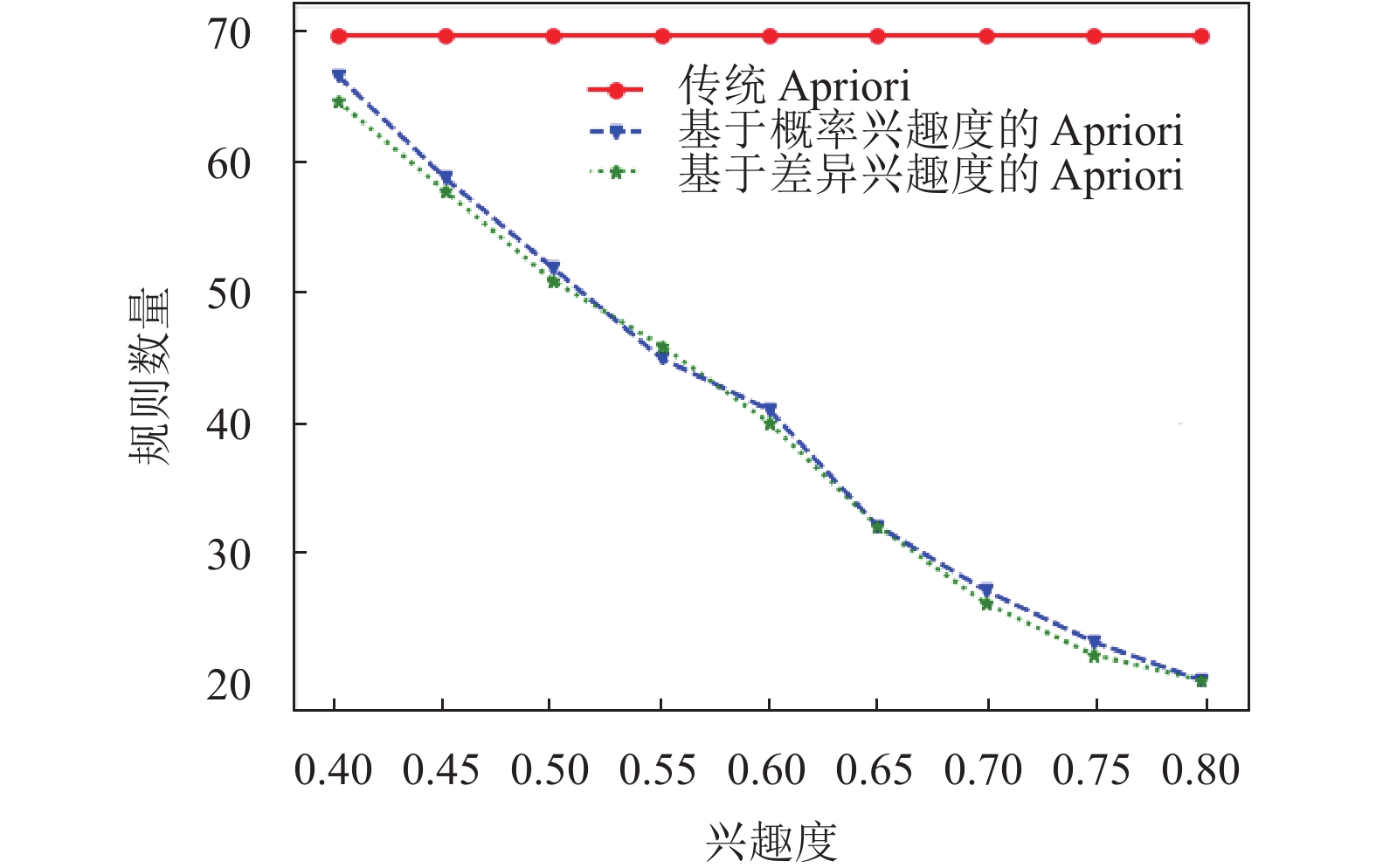
|
图 4 不同兴趣度下3种算法提取规则数量比较(Smin= 0.2, Cmin=0.3) |
综上所述, 使用本文算法较使用传统Apriori算法以及概率Apriori算法提取的规则数量少, 能够有效抑制无意义的误导性关联规则的产生, 提高了数据挖掘的效率和数据中隐含的知识的精确性.
(2)提取的规则解析
设定支持度
根据获得的关联规则, 绘制课程评价关联规则网络图, 以直观了解课程指标间的关系以及不同指标的重要性差异, 见图5. 由18条强关联规则构成的网络图中, 点代表课程评价指标, 点的大小取决于点的粗度; 边为有向边, 由规则前件指向规则后件, 边的粗细由规则的置信度决定, 越粗代表置信度越大; 各点之间的连通反映了各指标之间的影响.
| 表 6 提取的部分强关联规则及其解析(Smin=0.2, Cmin=0.45, Imin=0.5) |
考察提取到的关联规则, 可以发现人的因素对于课程建设的重要性. 表6中的规则1至4显示, 在一支教学团队中, 可通过发挥教师的能动性, 提升教材选用、教学改革及教学设计等的质量. 由此启发高校的教学管理者, 应在课程建设过程中, 注意发挥人的中心地位, 对课程负责人和主讲教师的遴选给予足够重视. 对于教师团队建设, 应优先选用学历高教龄长的教师出任课程负责人, 同时保持学历结构和年龄结构等的平衡, 以提高课程教学设计、教学改革与研究的水平, 奠定教学质量提升的基础.
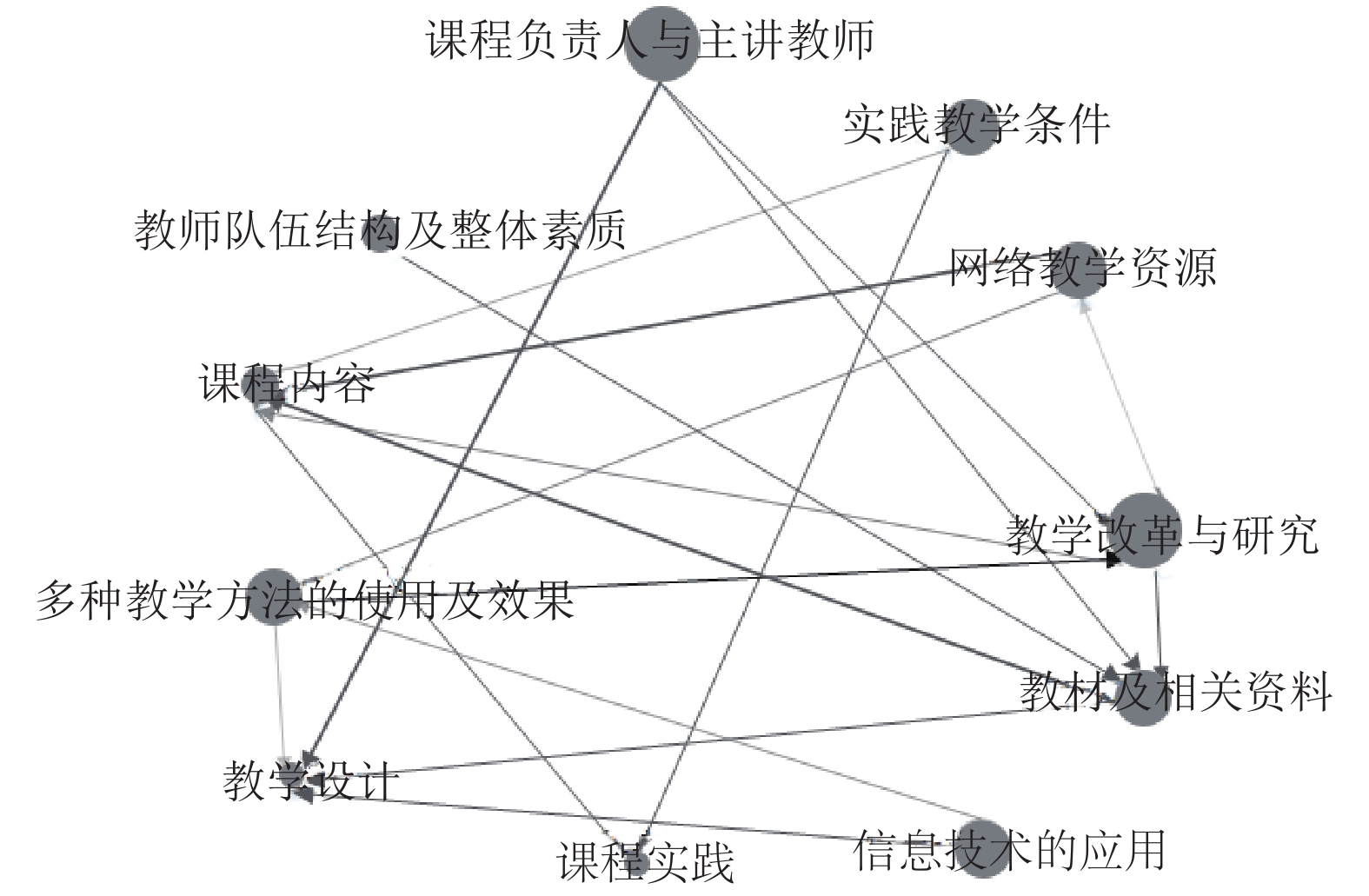
|
图 5 课程评价指标间的关联规则网络图 |
接着考察教学资源对课程建设的物质保障作用. 表6中的规则5, 6及规则9显示, 各类教学资源对于课程内容遴选、教学设计等具有基础性物质保障作用. 由此启发高校的教学管理者, 在课程建设中, 资源配置要更多地向教学资源倾斜. 特别是, 在教育部倡导并加大线上线下混合式一流课程建设力度的今天, 网络教学资源的重要性愈发凸显. 若在网络教学资源建设方面掉队, 人的作用纵然能充分发挥, 也难免会有“无米之炊”之虞.
最后考察信息技术和教学方法对课程建设的支撑性作用. 表6中规则7, 8显示, 信息技术和多种教学方法的综合使用, 有利于提高教学设计、教学改革与研究的水平. 反之, 信息技术素养欠缺, 以及基于信息技术教学方法落伍, 将以较大概率导致教学设计质量变差. 作为高校的教学管理者, 应重视教学方法和信息技术在发挥教师能动性和教学资源物质保障作用中的支撑和桥梁作用, 一方面提高学校的教育信息化建设水平, 另一方面, 通过加强建设信息技术的校园文化, 营造学习和提高信息技术水平的氛围, 同时引进社会资源, 加大教师培训力度, 提高教师的信息化素养, 掌握更多的基于现代信息技术的工具使用技能.
4 结论从服务课程建设的目的出发, 对数据驱动的课程评价方法进行研究. 通过挖掘多维度课程评价数据, 提取隐含的知识和模式, 将发现的知识用于指导课程建设, 辅助教学管理决策. 在不同支持度、置信度和兴趣度下, 使用改进Apriori算法对课程评价数据进行关联规则挖掘的结果, 与使用传统Apriori算法所得结果的比较显示, 本文方法能明显抑制误导性规则的生成, 提高挖掘效率, 增强隐含在多维度评价数据中知识指导的精准度. 未来研究, 将重点围绕高等教育领域更多的数据驱动管理决策需求和数据挖掘效率提升展开.
| [1] |
吴岩. 一流本科一流专业一流人才. 中国大学教学, 2017(11): 4-12, 17. DOI:10.3969/j.issn.1005-0450.2017.11.002 |
| [2] |
陈翔, 韩响玲, 王洋, 等. 课程教学质量评价体系重构与“金课”建设. 中国大学教学, 2019(5): 43-48. DOI:10.3969/j.issn.1005-0450.2019.05.010 |
| [3] |
陈国青, 曾大军, 卫强, 等. 大数据环境下的决策范式转变与使能创新. 管理世界, 2020, 36(2): 95-105. DOI:10.3969/j.issn.1002-5502.2020.02.009 |
| [4] |
许晓东, 陈金江. 国家精品课程评审指标修订及其启示. 中国高等教育, 2010(7): 38-39, 47. |
| [5] |
任高举, 白亚男. 关联规则挖掘在高校教学评价中的应用. 计算机与数字工程, 2014, 42(8): 1526-1529. DOI:10.3969/j.issn1672-9722.2014.08.051 |
| [6] |
郭鹏, 蔡骋. 基于聚类和关联算法的学生成绩挖掘与分析. 计算机工程与应用, 2019, 55(17): 169-179. DOI:10.3778/j.issn.1002-8331.1902-0223 |
| [7] |
李广璞, 黄妙华. 频繁项集挖掘的研究进展及主流方法. 计算机科学, 2018, 45(S2): 1-11, 26. |
| [8] |
王桌芳, 赵会军, 李聪, 等. 基于兴趣度度量的多类差异数据关联规则挖掘. 计算机应用与软件, 2019, 36(12): 60-65, 105. DOI:10.3969/j.issn.1000-386x.2019.12.010 |
| [9] |
谢雨婷. 基于学生成绩的课程关联性和学生综合素质评价研究[硕士学位论文]. 武汉: 华中师范大学, 2019.
|
| [10] |
郑丽生. Apriori改进算法在教学评价中的应用[硕士学位论文]. 泉州: 华侨大学, 2015.
|
| [11] |
周皓峰, 朱扬勇, 施伯乐. 一个基于兴趣度的关联规则采掘算法. 计算机研究与发展, 2002, 39(4): 450-457. |
 2021, Vol. 30
2021, Vol. 30



