2. 温州医科大学附属第二医院 信息中心, 温州 325000;
3. 温州医科大学附属第一医院, 温州 325000
2. Information Center, the Second Affiliated Hospital of Wenzhou Medical University, Wenzhou 325000, China;
3. The First Affiliated Hospital of Wenzhou Medical University, Wenzhou 325000, China
缩宫素, 又称催产素(OxyTocin, OT), 是产科催产、引产的一线药物, 具有启动分娩, 促进子宫收缩、加快产程的作用[1]. 临床上OT催产、引产的使用方式为静脉滴注, 需要医务人员实时观察子宫收缩及胎心率变化情况, 并结合产程进展、产妇脉搏和血压、出入液量平衡等因素, 每隔15–20 min调节一次OT微泵的输注速度, 注射速度根据等差法每次增加或减少5滴(给药速率恒定)[2]. 因此根据临床实际用药情况, 将剂量调节情况可分为: “维持原剂量”、“增加剂量”和“减少剂量”, 表明OT给药的走向.
但由于妊娠末期产妇对于OT的敏感性不同, 其输注剂量也存在差异, 若使用剂量过大会引起宫缩过强、过密、胎心减速, 甚至强直宫缩、胎儿窘迫死亡等不良妊娠结局[3], 使用剂量不足则无法达到预期临床效果. 因此, 为保证OT用药安全性和有效性的关键在于实现OT剂量的精准调控.
临床上依据《中华医学会产科学组分娩指南》对产时OT剂量进行调控, 通过持续电子胎心监护仪(Electronic Fetal Monitoring, EFM)的外部宫缩探头和超声多普勒探头测量宫缩压力和胎心率变化[4]. 但在分娩量激增和助产士短缺的现状下, OT剂量无法得到及时合理的调整[5], 且调控过程中亦受医护人员主观因素(如性格、临床经验、用药习惯)的影响. 目前已有将计算机方法应用于OT自动调控的相关研究, 如郑园园等(CN206434657U)开发了一种缩宫素注射自动调节装置[6], 将胎儿监护仪和输液泵通过单片机数据连接, 实现输液泵输注速度根据子宫收缩强度来调节, 当胎心率超出正常范围或出现异常宫缩时能发出警报. 韦晓昱等(CN203802891U)设计了一种产科用催产素自动点滴调节装置[7], 通过压力传感器采集的宫缩频率及强度信号, 经 DSP芯片的CPU 单元, 通过信号放大及驱动电路输出控制信号给输液泵. 但上述研究并未进行详尽的产时数据分析, 亦未建立相关预测模型, 仅根据既定的预设规则判断调控OT剂量, 起到简单预警作用. 而Lobo等则基于OT药代动力学方法, 模拟宫缩频率、宫腔压力、宫口扩张、胎先露与OT浓度之间的相互作用, 并根据输入变量的实时变化自动调节OT剂量[8], 但该研究只对模型效果进行初步的可行性分析, 未提及明确的评价或验证方案.
本研究提出一种智能OT剂量调控方法, 对胎心监护仪的宫缩信号进行特征提取, 结合胎心、心率、电子病历等数据, 基于贝叶斯优化的LightGBM算法构建OT剂量预测模型, 为产科医护人员OT剂量调控提供辅助决策支持, 减轻人力成本, 实现精准给药.
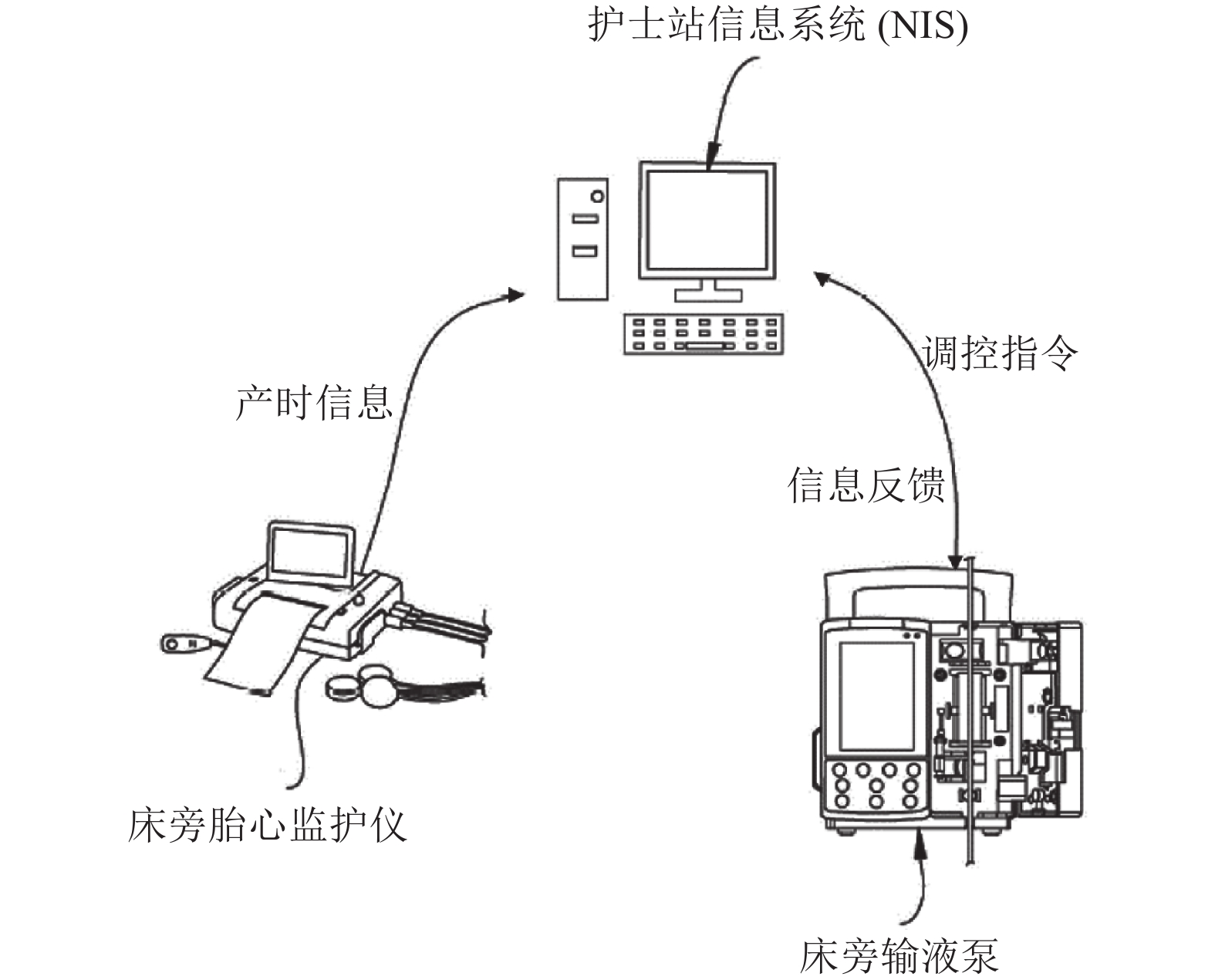
1 智能缩宫素注射反馈系统本研究课题组前期利用4G网络建立了一种缩宫素注射泵反馈系统[9], 如图1所示. 本系统以4G互联网技术为载体, 将电子胎心监护仪、输液注射泵、护士站远程监控相互连接, 通过胎心监护仪采集产妇宫缩及胎心变化信息, 由物联网技术远程反馈至护士站进行数据汇总, 最后在护士站将发出调控指令, 控制产妇床旁输液微泵, 调控注射速度.
|
图 1 智能缩宫素注射反馈系统结构图 |
本文建立的OT剂量预测模型可嵌入护士站系统作为数据分析中心, 实现智能调控输液微泵, 形成一套能便于监测子宫收缩及胎心率变化、智能调节OT输注、人工辅助监测的调节系统.
2 产时缩宫素剂量预测方法首先获取电子健康病历系统、护理管理系统和胎心监护仪设备输出的医疗数据, 并对宫缩信号进行特征提取; 其次对数据进行预处理, 最后基于贝叶斯优化的LightGBM算法构建产时OT剂量预测模型.
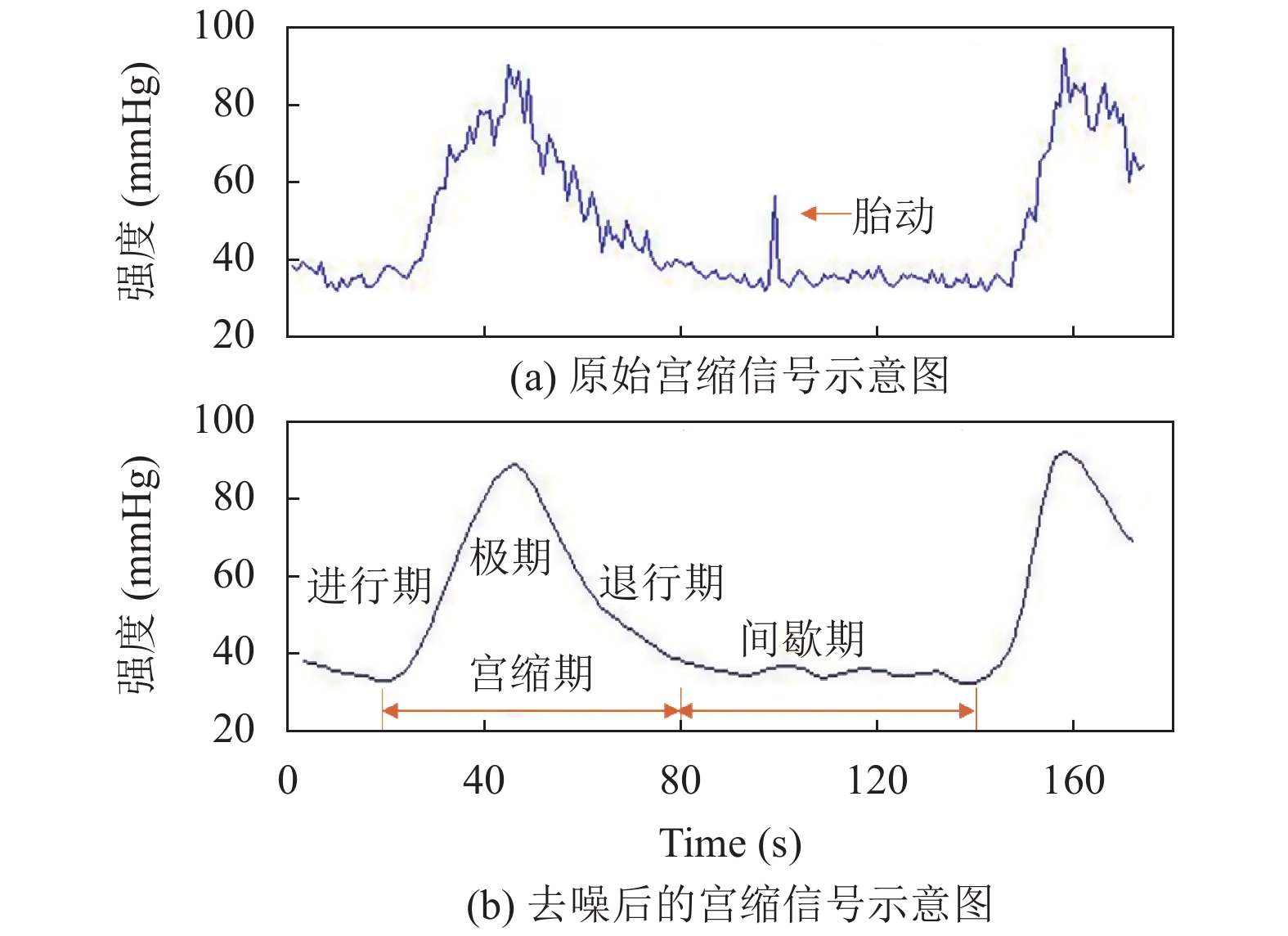
2.1 宫缩信号特征工程 2.1.1 宫缩信号利用床旁胎心监护仪实时采集宫缩信号, 其原理将压力传感器作为宫缩探测器, 根据宫缩压力大小反应宫缩情况. 采集过程中将压力传感器置于孕妇宫底部, 当子宫肌肉收缩时, 腹壁的张力置于传感器将宫缩压力信号转变成电信号. 压力电信号再经信号调理、模数转换等处理, 输出至监控端进行分析. 通常对宫缩信号的强度、持续时间以及宫缩周期3个方面加以描述. 每一次宫缩周期可分为3个阶段: 进行期、极期、退行期, 宫缩结束后则进入间歇期, 如图2所示.
|
图 2 小波去噪后的宫缩信号示意图 |
2.1.2 信号预处理
宫缩信号采集过程中受压力探头放置位置、腹部皮下脂肪厚度、胎动、探头绑缚的松紧、产妇活动等影响出现干扰信号, 影响宫缩波形的判读, 在去噪声的同时需尽可能保留信号中反应宫缩状况的特征, 本文采用基于小波滤波的信号平滑处理, 效果如图2 所示. 采用Sym6小波包, 对实测信号进行4尺度分解, 并将分解出的概貌系数做为去噪后的宫缩信号.
| $ {w_\Psi }f\left( {a,b} \right) = {\rm{d}}x\frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {f\left( t \right)} \Psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t $ | (1) |
小波滤波器表示成小波函数Ψ(t)在做位移b后, 在不同尺度a下与宫缩信号f(t)的内积波后恢复出宫缩信号的时域图.
2.1.3 信号特征提取分娩期产妇子宫收缩起自两侧子宫角部, 迅速向子宫底部集中, 再以2 cm/s的速度向下逐渐减弱, 每次宫缩由弱渐强(进行期), 维持一定时间(极期), 随后由强减弱(退行期), 直至消失进入间歇期, 间歇期子宫肌肉松弛, 宫缩如此反复, 直至分娩结束[10]. 宫缩峰值为一次宫缩最强压力点, 宫缩的提取需先定位宫腔压力峰值点, 算法过程具体如算法1.
算法1. 信号特征提取
C←Candiadate point Set
M←Maximum point Set
P←Peak point Set
Pavg←the average value ofP
I←Minimum interval of contractions
max(input:C; output:L)
for (k=2;
if
L←
endif
endfor
L←max(C)
P←
return
确认峰值点后, 根据其时域上的先后分布确定宫缩起始点和宫缩终止点: 为时序上峰值点相邻的两个处于基线水平的极小值点, 如图3所示. 将峰值点的幅值作为宫腔压力峰值, 单位时间与平均峰值间隔的比值作为宫缩频率, 宫缩起始点和宫缩终止点的间隔作为宫缩持续时间.

|
图 3 宫缩信号的特征提取图 |
确定宫腔压力、宫缩频率、宫缩持续时间后, 利用K-means聚类方法区分宫缩强度, K-means算法首先设定值作为聚类的初始中心点(k=3); 然后计算其他点到这 k个中心点的距离, 对靠近它们的点进行归类, 距离计算公式如下:
| $ d = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} } $ | (2) |
最后通过求平均值的方法迭代逐次更新各聚类中心的值, 直至各类中心点的值均不再变化, 本文的聚类效果如图4所示.
2.2 实验数据及其预处理通过文献综述和专家咨询法, 首先从电子病历系统获取与OT剂量调节相关的人口学资料, 包括: 年龄、BMI、孕周等, 经单因素分析和多重线性逐步回归, 筛选出具有统计学意义的特征. 其次, 通过访问飞利浦胎心监护仪(M2702A)数据端口获取产时生理参数, 包括实时胎心、产妇心率和宫缩特征(经2.1节提取). OT调节记录则通过护理信息平台获取, 调节信息包括当前OT用药剂量和累计调节时间.

|
图 4 K-means宫缩强度特征提取 |
OT用药每隔约15 min调整一次, 整合人口学数据和该时间段的生理参数调节记录, 作为一条记录样本纳入数据集, 产时生理参数包括胎心、宫缩频率、宫缩持续时间、宫缩强度、宫腔压力峰值在15 min内的平均值. 纳入模型的数据格式如表1所示.
| 表 1 缩宫素剂量预测模型数据集 |
产妇年龄、BMI等人口学资料缺失值填补可通过人工校验原始数据, 所有数据采用Rajda标准[11]进行异常值处理, 即以给定的置信概率99.7%为标准, 以3倍数据列标准差为依据, 删除大于该值的异常数据.
2.3 贝叶斯-LightGBM缩宫素剂量预测模型 2.3.1 LightGBM建模LightGBM是2017年微软亚洲研究院发布的一种基于决策树算法的快速、分布式、高性能梯度提升框架, 目前广泛应用于分类、回归等多种产科医疗数据分析的应用场景, 如妊娠糖尿病的早期筛查[12]和胎儿出生体重的预测[13].
梯度提升树核心思想是利用损失函数的负梯度在当前模型Fm(x)=Fm−1(x)的值近似替代残差. 设训练样本为i(i=1, 2, 3,…,n), 迭代次数j (j=1, 2, 3,…,m), 损失函数为L(yi, F(xi)), 则负梯度rij的计算公式如下:
| $ {r_{ij}}{\rm{ = }}{\left[ {\frac{{\partial L\left( {y,F\left( {{x_i}} \right)} \right)}}{{\partial F\left( {{x_i}} \right)}}} \right]_{F\left( x \right) = {F_{j - 1}}\left( x \right)}} $ | (3) |
使用基学习器hj(x)拟合损失函数的负梯度r, 求出使损失函数最小的最佳拟合值:
| $ {r_j}{\rm{ = }}\mathop {\mathop {\rm argmin}\limits_r \sum\limits_{i = 1}^n {L\left( {y,{F_{j - 1}}\left( x \right) + {h_j}\left( {{x_i}} \right)} \right)} }\limits_{} $ | (4) |
从而进行模型更新, 本轮的强学习器如下:
| $ {F_j}\left( x \right) = {F_{j - 1}}\left( x \right){\rm{ + }}{r_j}{h_j}\left( {{x_i}} \right) $ | (5) |
最终梯度提升树是由每轮产生的基学习器通过线性相加的方式求得:
| $ {F_M}\left( x \right) = \sum\limits_{j = 1}^m {{F_{j - 1}}\left( x \right)} $ | (6) |
LightGBM是对传统梯度提升树的优化, 基于单边梯度采样(Gradient-based One Side Sampling, GOSS)算法减少训练的样本数, 并采用互补特征压缩(Exclusive Feature Bundling, EFB)算法减少特征维数, 且支持 GPU 并行学习. 因此基于LightGBM的建模在不牺牲数据处理速度的前提下, 最大限度地减少通信时间, 降低其带来的损失, 在计算上实现线性加速.
GOSS算法可保持信息增益估计的准确, 信息增益使用分裂后的方差增益衡量, 只保留那些具有较大贡献的样本, 方差增益Vj(d)如下:
| $ {V_j}\left( d \right) \!=\! \dfrac{1}{n}\left(\!\! {\dfrac{{{{\left( {\displaystyle\sum\limits_{{x_i} \in {A_l}} {{g_i}} \!+\! \dfrac{{1 \!-\! a}}{b}\displaystyle\sum\limits_{{x_i} \in {B_l}} {{g_i}} } \right)}^2}}}{{n_l^j\left( d \right)}} \!+\! \dfrac{{{{\left( {\displaystyle\sum\limits_{{x_i} \in {A_l}} {{g_i}} \!+\! \dfrac{{1 \!-\! a}}{b}\displaystyle\sum\limits_{{x_i} \in {B_l}} {{g_i}} } \right)}^2}}}{{n_r^j\left( d \!\right)}}} \!\right) $ | (7) |
其中, d是样本特征的分裂点, n表示样本数, A、B表示分裂的大、小梯度样本, l、r表示左子树和右子树, g表示样本梯度.
EFB算法则可减少高维数据的特征数目并且使损失最小, 采用直方图(Histogram)算法把连续浮点型特征值离散化, 将其作为索引在直方图中累积统计量, 通过捆绑合并相互独立的特征减少特征的数量, 由此降低模型的内存占用和时间复杂度.
在大数据背景下, 产科临床数据资料呈持续爆炸性增长, LightGBM在面对复杂而多元化的大数据时处理能力更优秀, 其信息资源占用率低且运行高效, 因此本研究拟选用LightGBM构建预测模型.
2.3.2 贝叶斯优化贝叶斯优化算法是一种高效的参数优化算法, 可以统一将此问题描述为求解未知目标函数的全局最优解:
| $ {x^*}{\rm{ = }}\mathop {\rm argmin}\limits_{x \in X} f(x) $ | (8) |
其中, x表示待优化参数, X表示参数集合; f(x)表示目标函数.
贝叶斯优化主要分为两个步骤. 首先确定先验函数, 以表示被优化函数的分布假设, 通常选用兼具灵活性和可追踪性的高斯过程(Gaussian processes); 其次选择提取函数(acquisition function), 在模型后验分布中构造效用函数, 以确定下一个需评估的点.
高斯过程此处为LightGBM算法中不同的参数组合在随机过程上的扩展, 它由一个均值函数m(x)和一个半正定的协方差函数k(x, x')组成:
| $ m\left( x \right) = E[f\left( x \right)] $ | (9) |
| $ k\left( {x,x'} \right) = E\left[ {\left( {f\left( x \right){\rm{ - }}m\left( x \right)} \right)\left( {f\left( {x'} \right){\rm{ - }}m\left( {x'} \right)} \right)} \right] $ | (10) |
为便于计算, 通常取均值函数m(x)=0, 则存在一个高斯分布满足:
| $ f\left( x \right) \sim GP\left( {m\left( x \right),k\left( {x,x'} \right)} \right) \to f \sim N\left( {0,K\left( {X,X} \right)} \right) $ | (11) |
当加入新样本X*, 可利用协方差矩阵K(X, X)生成一个新的高斯分布:
| $ K\left( {X,X} \right) = \left( {\begin{array}{*{20}{c}} {k\left( {{x_1},{x_1}} \right)}& \cdots &{k\left( {{x_1},{x_n}} \right)} \\ \vdots & \ddots & \vdots \\ {k\left( {{x_n},{x_1}} \right)}& \cdots &{k\left( {{x_n},{x_n}} \right)} \end{array}} \right) $ | (12) |
| $ {f^*} \sim N\left( {0,K\left( {{X^*},{X^*}} \right)} \right) $ | (13) |
高斯过程的性质可得, 训练输出f和测试输出f*的联合分布为:
| $ \left( \begin{gathered} f \\ {f^*} \\ \end{gathered} \right) \sim N\left( {0,\left[ {\begin{array}{*{20}{c}} {K\left( {X,X} \right)}&{K\left( {X,{X^*}} \right)} \\ {K\left( {{X^*},X} \right)}&{K\left( {{X^*},{X^*}} \right)} \end{array}} \right]} \right) $ | (14) |
通过评估均值和协方差矩阵, 可以从联合后验分布中对函数值f*进行采样, 通过采样函数确定下一个需要评估的点, 可以减少迭代次数, 降低评估成本. 采样点提取有如下两类方法: (1) explore, 尽可能选取未评估过的参数组合; (2) exploit, 根据目前已找到的最优值, 在其周围搜索找到全局最优值.
贝叶斯优化中常见的采样函数包括POI (Probability Of Improvement), EI (Expected Improvement)和UCB (Upper Confidence Bound), 本文选择UCB作为为采样函数, 其表达式为:
| $ UBX\left( x \right) = \mu \left( x \right) + \beta \sigma \left( x \right) $ | (15) |
其中,
收集2019年1月–2019年12月于浙江省某三甲医院产科分娩并在产程中使用OT的产妇相关资料, 由统一培训的6人组成数据收集小组, 以开始滴注OT为起点, 停止输注为终点, 采集这一过程中影响医务人员进行OT调节的相关数据, 包括电子病历与护理记录资料, 其中胎心监护资料通过访问飞利浦胎心监护仪数据端口获取(具体见2.3.1节). 共纳入998例产妇的10061条OT调节记录, 其中标签为OT“剂量维持”的3467条, “剂量增加”6178条, “剂量减少”416条.
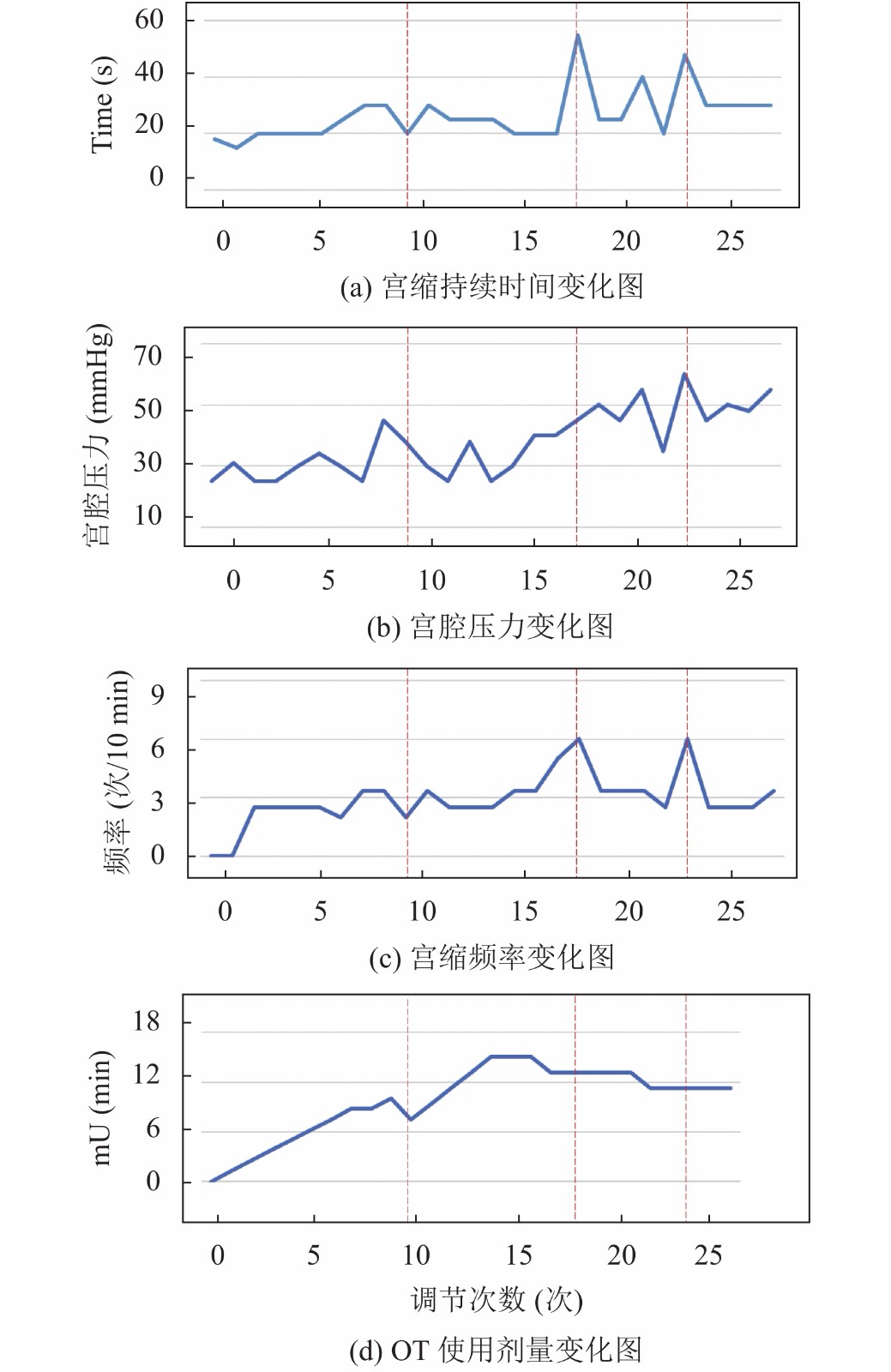
3.2 宫缩信号结果分析图5为本研究OT剂量调节与宫缩持续时间、宫腔压力、宫缩频率相关性的个案分析, 选择1名受试者静息状态下持续性输注OT时的宫缩信号, 采集时间约8 h, 横坐标代表这一过程中每隔约15 min进行OT剂量调整的次数, 纵坐标分别代表宫缩持续时间、宫腔压力、宫缩频率和用药剂量. 由图可知, 0–9次OT剂量逐渐增加, 相应的宫缩频率、宫腔压力、宫缩持续时间均处于较低水平, 且有上升趋势; 第10次减少剂量时, 宫缩频率、宫腔压力、宫缩持续时间出现明显下降趋势; 15–20次OT达到最高剂量, 宫缩频率、宫腔压力、宫缩持续时间也均出现峰值. 可见本文宫缩信号提取的特征和OT用药调整高度相关.
|
图 5 宫缩信号与OT用药对比图 |
3.3 实验过程和评价指标
10061条OT调节记录按照8:2分为训练集8049条和测试集2012条, 采用5折交叉验证的方法进行分析和预测. LightGBM参数较多, 基于交叉验证的手动调参操作复杂且易影响预测效果, 本文采用贝叶斯优化(BOA)方法调整最佳参数. LightGBM主要包含3类参数: Booster参数、通用参数和学习目标参数, 表2为本文需调整的几个核心参数的含义及取值范围, 其它参数均为默认值, 设置迭代次数为200, 最终LightGBM选择学习率0.05, 叶子数51, 树最大深度5, min_data_in_leaf =20, bagging_fraction=0.9, feature_fraction=0.8.
本研究选择模式识别常用的评价指标: 准确率(accuracy)、查准率(precision)、召回率(recall)和F1值对各个模型的性能进行评价, 此外, 还采用混淆矩阵观察模型在各个类别上的表现.
3.4 预测结果和分析同时选用5种机器学习算法包括逻辑回归(LR)、支持向量机(SVM)、多层感知器(MLP)、随机森林(RF)、梯度提升树(GBDT)进行对比, 均按照8:2 将数据集划分为训练集和测试集, 通过5折交叉验证实验结果. 与交叉验证试错法调参的LightGBM相比, 经贝叶斯优化的BOA-LightGBM模型对OT剂量调控的预测能力最佳, 其准确率为0.83, 查准率0.853, 召回率0.828, F1值0.84, 均优于其他对照机器方法(见表3).
| 表 2 LightGBM各参数的含义及取值范围 |
| 表 3 不同模型预测性能对比表 |
分类预测结果的混淆矩阵如表4所示: 列表示真实类别, 行表示预测类别, 混淆矩阵表明 LightGBM模型可对“减少剂量”进行有效预测, 准确率达97%以上, 而误差集中在“剂量增加”和“剂量维持”的预测, 主要原因可能是临床上对产妇“剂量增加”的决策较为保守, 需谨慎控制OT用量以避免潜在的不良反应; 此外, OT的调控还受产妇主诉(孕妇主诉反应有疼痛感时一般不会增加剂量)和医护人员的主观因素(性格、临床经验、用药习惯)影响, 因此对“剂量增加”和“剂量维持”的辨别较弱.
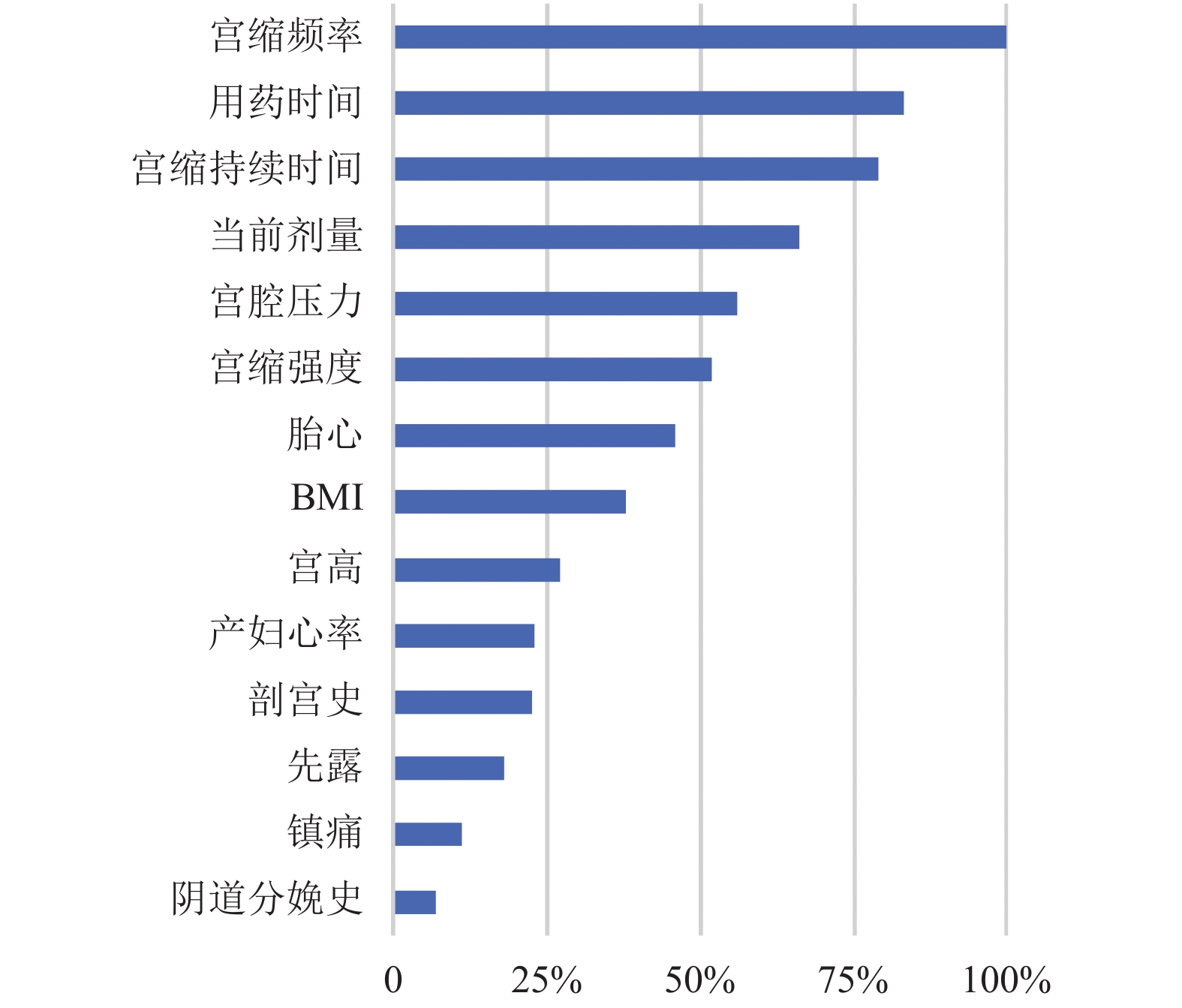
LightGBM特征重要性排名如图6所示, 通过输出特征重要程度, 可以判断哪些因素对OT调节有更显著的影响, 从而辅助医护人员进行用药决策. 宫缩频率、宫缩持续时间、宫腔压力、宫缩强度、胎心是最终模型结果中最重要的特征, 与临床实际医务人员进行OT调控及指南要求观察的指标一致[2], 表明本模型高度模拟临床思维, 使建模结果具有较高的可信度. 用药时间、当前剂量、产妇年龄、BMI、分娩镇痛、胎先露、剖宫产史及阴道分娩史均为影响OT输注剂量的影响因素[14-17], 这些数据较全面的反映了产妇分娩时的状态, 为模型精度提供保障. 目前OT的输注仍依靠医护人员通过胎儿电子监护母儿情况实施人工调节, 但由于影响因素众多、关系复杂且不够直观, 对缺乏临床经验的医务人员而言, OT剂量的调控难以把控. 因此, 基于本模型的OT调控系统可为医务人员产时OT用药提供决策支持, 代替或减轻医护人员在OT输注中的作用, 减少人力成本, 实现精准给药, 更兼顾用药安全性和有效性.
| 表 4 缩宫素实际剂量调控情况与模型预测情况比较 |
|
图 6 纳入变量的重要性分布 |
4 结论与展望
本文从宫缩信号中提取宫腔压力、宫缩频率、宫缩持续时间, 结合胎心、心率、人口学资料和护理记录等数据, 基于贝叶斯优化的LightGBM算法构建产时OT剂量预测模型, 相比传统机器学习方法, 本文模型预测能力更佳. 将本文模型嵌入已有的智能缩宫素注射反馈系统, 可有效解决传统输注方案对个人经验的依赖和医务人员人力资源短缺的矛盾.
相较于传统的OT输注方案, 基于贝叶斯优化的LightGBM模型兼具精准调控和用药安全: OT输注调控实际是一种实时反馈调节, 目前需要医务人员依据胎心监护信息每隔15 min左右进行用药剂量的人工调整, 目前OT临床使用需求量大, 其对医务人员临床经验要求高、观察指标复杂, 而目前现有的OT输注反馈系统多以既定的预设规则进行预警, 尚未解决OT剂量智能化调控的实际需求. 本文模型首先对宫缩信号进行特征提取, 并基于临床OT真实用药情况进行模型训练, 精确度较高, 该模型可作为一种产科医护人员的辅助决策模块应用于产时护理, 是当前国内对OT输注调控的模式的创新, 今后研究中或将替代助产士进行OT输注, 为医院节省大量资源.
| [1] |
Kernberg A, Caughey AB. Augmentation of labor: A review of oxytocin augmentation and active management of labor. Obstetrics and Gynecology Clinics of North America, 2017, 44(4): 593-600. DOI:10.1016/j.ogc.2017.08.012 |
| [2] |
中华医学会妇产科学分会产科学组. 妊娠晚期促子宫颈成熟与引产指南(2014). 中华妇产科杂志, 2014, 49(12): 881-885. DOI:10.3760/cma.j.issn.0529-567x.2014.12.001 |
| [3] |
Sheibani L, Wing DA. A safety review of medications used for labour induction. Expert Opinion on Drug Safety, 2018, 17(2): 161-167. DOI:10.1080/14740338.2018.1404573 |
| [4] |
中华医学会妇产科学分会产科学组, 中华医学会围产医学分会. 正常分娩指南. 中华妇产科杂志, 2020, 55(6): 361-370. DOI:10.3760/cma.j.cn112141-20200426-00356 |
| [5] |
陈希, 张贵赋, 龙丽萍, 等. 52例缩宫素注射液致严重不良反应的文献分析. 中国药业, 2016, 25(22): 13-16. |
| [6] |
郑园园. 催产素注射自动调节装置: 中国, 206434657U. [2017-08-25].
|
| [7] |
韦晓昱. 产科用催产素自动点滴调节装置: 中国, 203802891U. [2014-09-03].
|
| [8] |
Lobo MF, Bastos LF, van Meurs WL, et al. A model for educational simulation of the effect of oxytocin on uterine contractions. Medical Engineering & Physics, 2013, 35(4): 524-531. |
| [9] |
朱晓玲, 项宁惠, 赵静苗, 等. 一种缩宫素注射泵反馈系统: 中国, 107854748A. [2018-03-30].
|
| [10] |
童慧玲. 基于胎儿监护的宫缩识别算法研究[硕士学位论文]. 杭州: 杭州电子科技大学, 2018.
|
| [11] |
张振慧, 张正江, 胡桂廷, 等. 基于拉依达准则与线性拟合的改进型无迹卡尔曼滤波粗大误差补偿算法. 计算机测量与控制, 2019, 27(11): 153-156, 162. |
| [12] |
Lu Y, Fu XH, Chen FX, et al. Prediction of fetal weight at varying gestational age in the absence of ultrasound examination using ensemble learning. Artificial Intelligence in Medicine, 2020, 102: 101748. DOI:10.1016/j.artmed.2019.101748 |
| [13] |
Wang Y, Wang T. Application of improved LightGBM model in blood glucose prediction. Applied Sciences, 2020, 10(9): 3227. DOI:10.3390/app10093227 |
| [14] |
陈宇, 郑晓莉, 伍绍文, 等. 不同年龄段高龄孕产妇临床特点与妊娠结局的分析. 中华妇产科杂志, 2017, 52(8): 508-513. DOI:10.3760/cma.j.issn.0529-567x.2017.08.002 |
| [15] |
Adams AD, Coviello EM, Drassinower D. The effect of maternal obesity on oxytocin requirements to achieve vaginal delivery. American Journal of Perinatology, 2020, 37(4): 349-356. DOI:10.1055/s-0039-1694982 |
| [16] |
Lipschuetz M, Cohen SM, Lewkowicz AA, et al. Prolonged second stage of labor: Causes and outcomes. Harefuah, 2018, 157(11): 685-690. |
| [17] |
王起兰, 林姝, 程卫平, 等. 引导硬膜外分娩镇痛产妇卧位调节对胎儿枕后位影响的研究. 中国实用护理杂志, 2018, 34(11): 809-813. DOI:10.3760/cma.j.issn.1672-7088.2018.11.002 |
 2021, Vol. 30
2021, Vol. 30



