2. 集美大学 计算机工程学院, 厦门 361021
2. Computer Engineering College, Jimei University, Xiamen 361021, China
随着现代互联网的不断发展, 网络规模持续扩大, 网络的使用也开始发展为全球化的方向. 在此背景下, 网络入侵攻击事件频发. 传统的防火墙技术无法对网络安全性进行保证, 所以需要实现网络入侵检测系统(IDS)的设计. 网络入侵检测系统指的是主动积极的安全防护技术, 其逐渐发展为网络安全领域研究的重点内容[1]. 在网络入侵检测系统工作过程中, 大部分为被动的监听, 利用关键网段得出网络传输数据包, 通过多种检测分析的方式对数据包进行分析, 从而寻找入侵的痕迹. 在网络入侵检测系统检测的时候, 并不会对网络性能造成影响, 还能够提高网络攻击事件定位的效果. 现代分析网络入侵检测系统的主要方法为基于特征、异常的检测, 由于异常检测过程中的学习时间比较长, 所以一般利用基于模式匹配特征检测[2]. 以此, 本文就对网络入侵检测系统的多模式匹配算法进行全面分析.
2 网络入侵检测 2.1 网络入侵检测的原理因为传统的安全策略无法有效满足安全的实际需求, 从而产生了入侵检测系统, 并且在发展过程中逐渐成为动态安全技术的代表, 使计算机安全领域的发展与研究有所促进. 入侵检测系统为计算机系统与网络中的安全事件检测的技术, 主要包括数据采集、分析与结果处理3个功能. 图1为入侵检测系统基本的结构.

|
图 1 入侵检测系统的基本结构 Fig. 1 The basic structure of IDS |
在网络入侵检测系统中, 数据分析模块是核心模块, 由于模式匹配原理简单、可扩展性好, 现代网络入侵检测系统利用广泛采用模式匹配的方法进行数据分析. 随着科技的日新月异, 网络的规模也不断扩大, 网络带宽量也逐渐增加, 要求网络入侵检测性能处理的效率得到改进, 否则会导致出现入侵漏报的情况, 也就无法充分发挥网络入侵检测系统的优势.
模式匹配算法应用于入侵检测领域, 是将攻击模式库中的攻击模式与待检测网络数据进行匹配, 若匹配成功则系统判断出现了网络攻击. 目前的模式匹配算法分为单模式和多模式匹配, 其中典型单模式匹配算法包括KMP算法和BM算法, 多模式匹配算法包括AC算法和AC-BM算法[3].
2.2 传统网络入侵检测算法在1977年, Boyer和Moore提出了BM算法[4], 促进了模式匹配算法的发展. 此算法在进行匹配时包含两个并行算法, 坏字符和好后缀算法, 目的是让模式串每次向右移动尽可能大的距离.
多模式匹配即在一个文本串中同时查找多个模式串, 较之单模式匹配更易应对不断扩大的入侵特征库, 因此现今主流的IDS使用的基本都是多模式匹配算法. AC (Aho-Corasick) 算法作为最经典的多模式匹配算法被许多IDS采用, 该算法包含预处理和匹配两个阶段, 将待匹配的入侵特征模式串转换为树状有限状态自动机, 然后进行扫描匹配.
BM算法是一种性能较好的模式匹配算法, 该算法在不匹配的情况下可以产生跳跃, 从而减少匹配次数, 但无法满足日益复杂的网络入侵类型; AC算法记录的自动机耗费了大量的存储空间. 此外, AC与BM网络入侵检测算法具有较大的漏配量和无效配的情况, 降低系统的检测精准率与匹配速度, 所以就要对网络入侵检测算法进行改进[5].
3 检测系统模式匹配算法优化 3.1 单模式匹配算法的改进1980年, Horspool提出了改进的BM算法[6], 也就是BMH算法. 简化了BM算法, 执行方便, 效率也有所提高. 有n长度的文本字符串T 与m长度的模式字符串P. 在改进BM算法过程中, 不匹配过程中的正文与模式移动距离有所扩大. 它不再像BM算法一样关注失配的字符, 它的关注的焦点在于匹配文本每一次匹配失败的最后一个字符X, 根据这个字符X是否在模板出现过来决定跳跃的步数, 否则跳跃模板的长度. 如果字符X不在模式P中, 则跳跃的步数为模式P的长度, 字符X在模式P中, 跳跃的步数为字符X距离离尾部最近的字符X的距离(不包括最后一个字符).
| $ \begin{split} &{{dist[X] = }}\left\{ \begin{array}{l} m{{;X}}{\text{字符在}}{{P}}{\text{中未出现}}\\ m{\rm{ - }}j{{; X}}{\text{字符在}}{{P}}{\text{中出现}} \end{array} \right\}\\ &j = \max\{ j|P\left[ j \right] = x,1 \le j \le m - 1\} \end{split} $ | (1) |
利用dist函数的分析表示,

|
图 2 模式正文匹配示例 Fig. 2 Pattern matching example |
本文改进算法的主要思想为:
首先, 假设变量k为模式第一次与最后一次的匹配字符, 将BM算法作为基础, 在出现不匹配的时候, 能够实现T [k+1]的判断. 如果出现T [k+1], 那么模式移动距离假设为L, 规定
全面考虑从右到左的正文与模式匹配, 模式右边的字符匹配大于左边. 假如具有长模式的情况, 和左边不匹配时候进行对比, 需要的时间成本量比较大. 为了方便算法的实现, 在本文中实现针对性方案的设计. 在算法改进之前对比正文位置字符与模式首字符, 如果不匹配直接判断T [k+1], 继续下个匹配过程. 之后根据以上改进算法实现匹配对比, 降低不必要匹配过程, 从而节约匹配时间[9].
3.2 多模式匹配算法的改进网络入侵检测系统能够深入检测执行数据包, 并且全面扫描负载或者已经定义规则集的匹配模式串, 检测是否具备入侵检测事件[10].
3.2.1 分析算法的后缀函数在BM算法中, 在匹配过程中比较了一个模式的长度, 而且存在之前匹配的结果, 在后面的匹配过程中被“遗忘”的情况, 模式串长度越长效率越低. 本文使改进的BMH算法和传统BM算法实现实验对比, 此实验主要包括的测试指标为BM与改进BMH算法字符数量、运行的时间和BM算法字符比较数量和使用后缀规则数量.
因为入侵检测实现自检, 其模式串的长度设置为20–30字符. 本文通过随机的选择开展实验, BM与改进BMH算法的运行时间比详见表1. 通过表可以看出来, 两种算法的总字符数量是相同的, 但是基于时间复杂度中, 改进BMH的性能更加良好.
3.2.2 算法描述基于传统BM算法, 充分考虑文本串中的字符T [j]并不会出现在模式串中, 如果其下个字符T [j+1]和模式串中的首字符P[1]相同, 也就是T [j+1]=P[1], 以此创建滑动距离函数2, 简化判断的过程, 使比较次数降低, 提高匹配的效率. 在分析传统BM模式匹配算法过程中, 模式串中出现重复字符的时候会导致指针回溯的问题, 那么在本文函数中使用“取子串”的方法能够避免出现指针回溯的问题[11]. 算法流程如算法1.
| 表 1 BM与改进BMH算法运行的总时间对比(单位: s) Table 1 Algorithm running time comparison |
算法1. FBM模式匹配算法
输入: 文本串T, 模式串P
输出: 文本串T中模式串P的出现起始位置
1. 假如此文本串中从位置j开始往左一个子串和模式串开展从右到左对比, 如果出现不匹配的情况, 就要调用滑动距离函数
2. 假如T [j]在P, 在算法过程中重新匹配正文中的
3. 假如T[j]并没有处于P中, 那么j=j+1并且对滑动距离函数Slide2(T[j])调动;
4. 对步骤3反复的进行, 直到对匹配位置寻找后才能够进行匹配, 或者匹配的过程失败;
5. 将文本串T中的模式串输出P的起始位置[12].
BMH算法在改进过程中的重点为定义给定模式
Slide: C→{1,2,…,m}
其中, c∈∑(假设∑指的是所有英文字母集合)
Slide1指的是滑动距离函数设置为1, 其给出正文中的任意字符c在模式中的距离, 具体定义为:
| $ Slide1[c] = \left\{ {\begin{array}{*{20}{l}} { - 1,}&\begin{array}{l}{\text{如果任意字符}}C{\text{不出现}}P{\text{中}}\\{\text{或者}}{{c}} = {P_{{j}}}\left( {{{j}} = {{m}}} \right)\\{\text{但是}}{{c}} \ne {P_{{j}}}\left( {{\rm{1}} \le {{j}} \le {{m - }}1} \right) \end{array}\\ \begin{array}{l} \\ {{m - j}}, \end{array}&\begin{array}{l} \\{{j}} = {\rm{max}}({{j:}}{P_{{j}}} = {{c,}}1 \le {{j}} \le {{m - i - }}1)\\{{i}}{\text{指的是模式串失配的位置}} \end{array} \end{array}} \right. $ | (2) |
Slide2指的是滑动距离函数2, 其能够给出正文中会出现的任意字符位置, 具体定义为:
| $ \begin{split} & Slide2[c] = \left\{ {\begin{array}{*{20}{c}} { - 1,}&{{\text{若任意字符}}{{c}} \ne {P_{{i}}}}\\ {{{m - }}1,}&{{\text{若任意字符}}{{c}} = {{{p}}_{{j}}}} \end{array}} \right.\\ &\;\;\;{P}_{{i}}{\text{为模式串首}}字符 \end{split} $ | (3) |
预处理阶段在读入规则文件的时候, 使模式组划分成为多字节模式组与单字节模式组, 将两者添加到相应模式组中. 针对单字节模式串组, 预处理阶段不进行处理. 改进算法以多字节模式串组计算前缀和后缀索引、跳跃距离Shift表, 计算的方法为: 得出最短模式长度m, 使其成为匹配窗口大小. 取每个模式最后B个字符对Hash值计算,B个字符指的是一个块字符. Shift表中将字符串中全部块字符在T时的移动距离进行计算. 针对每个出现的多字节模式串中字符块, 使二维位图EXIST_P中的位置标记成为1, 其他标记成为0. 以此, 在匹配的时候如果查找文本字符块处于位图EXIST_P标记成为0, 那么此字符串并不会在多字节模式串组任何模式串中出现. 二维图计算方法为:
| $ \begin{split} & EXIST\_P(char1char2) = \\ &\left\{ \begin{array}{l} 1,char1char2{\text{在模式串中}}\\ 0,char1char2{\text{不在模式串中}} \end{array} \right. \end{split} $ | (4) |
以改进算法思想, 图3为改进算法的实现流程. 为了能够有效地简化流程, 数组下标为字符的位置[13].

|
图 3 改进算法的实现流程 Fig. 3 flowsheet of improved algorithm |
具体的流程为:
1) 对K≤n(n为待检测字符串T的长度)是否成立判断, 如果k<n, 那么在模式串长度比正文字符串长度要小, 此时就要对其进行匹配检查, 模式和正文对其, 对比正文位置字符和首字符. 假如出现不匹配的情况, 就到最后一步. 假如k>n, 匹配的过程失败, 程序就结束.
2) 从左到右匹配模式和正文, 并且对比, 如果模式字符串和正文字符串进行匹配, 对匹配的位置进行记录, 以此说明能够成功匹配, 结束程序. 假如某位置的字符串出现不匹配的情况, 就进入到步骤3).
3) 对目前的匹配操作进行判断, 模式中的正文和模式最后一位对应位置是否有下位字符, 以判断结果变量k值计算, 之后转到步骤1)[14].
处理阶段时间复杂度为O(m+σ), 其中σ为x与已匹配部分在P中的位置, 搜索阶段最坏情况下时间复杂度为O(mn), 模式字符串的长度大小将影响到时间复杂度, 一般文本字符的平均比较数在1σ和2/(σ+1)之间.
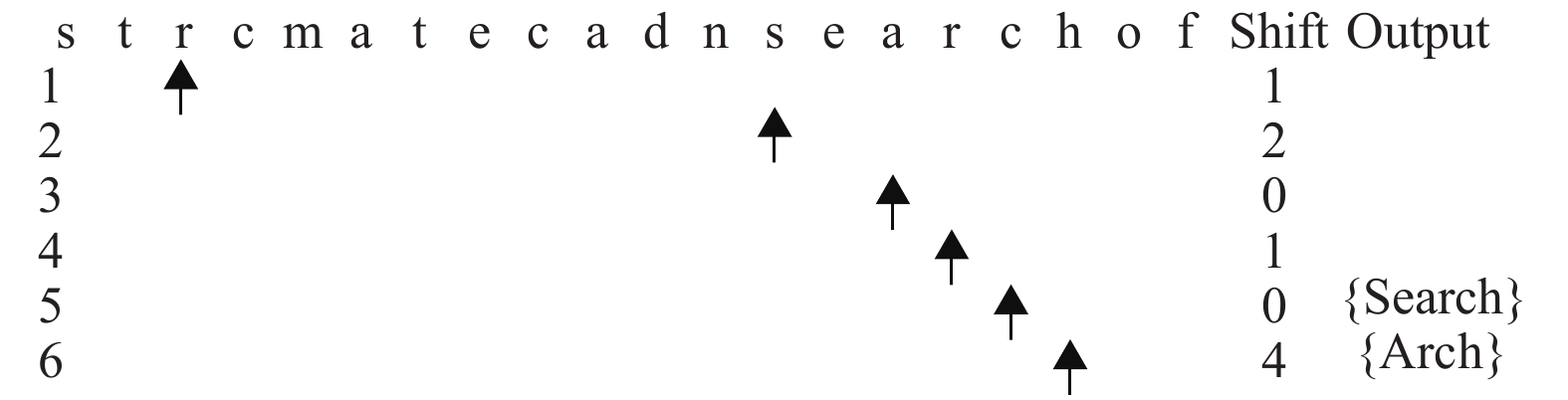
图4为改进算法的匹配过程, 算法以二维图判断某字符串是否在模式串中出现, 首先读入字符串“st”, EXIST_P(st)为0, 使窗口向后移动一位. EXIST_P(tr)值为0, 继续使窗口向右移动一位. EXIST_P(rc)值为1, 此处会出现匹配, 通过本文算法实现匹配, 查找Shift表, 后续文本串根据同样方法进行匹配.
|
图 4 改进算法的匹配过程 Fig. 4 Matching of improved algorithm |
通过上述匹配可以看出来, 使用原本算法匹配的时候, 要计算9次Hash值并且查找Shift表实现跳跃. 改进算法能够以位图判断此字符串是否处于模式串中. 在以上匹配过程中一共计算6次Hash值, 并且查找Shift表实现跳跃.
4 算法的实验和分析为了对今后算法性能进行校验, 本文用改进后算法和传统BM算法实现实验对比. 在Win 7环境中实验, 系统配置2.66 GHz Intel CPU. 实验过程中使用官网中的模式串, 以Snort匹配过程, 使所有规则文件规则字符串作为模式组, 在实验过程中依次使用此模式组对改进算法实现校验. 在查找文本通过MIT Lincoln实验室中的DARPA99数据集的数据构成, 通过DARPA99测试数据集中选择4 MB测试数据. 图5为在不同最小模式中的算法性能对比. 通过图5可知, 在模式串组中具备单字节模式串与两个字节模式串时, 改进算法性能有所提高.

|
图 5 不同最小模式中的算法性能对比 Fig. 5 Comparison of algorithm performance |
图6为不同模式串集的算法性能, 通过图6可知, 在模式串集模式串数量不断增加的过程中, 改进算法与原算法的性能相同. 但是在模式串数量比较少的时候, 改进算法的匹配运行时间比原算法的匹配运行时间要短. 在入侵检测系统中, 匹配规模集中规则数量不超过400条, 改进算法的应用价值良好. 增加到1200条时, 两种算法应用价值相当. 在2000条时, 改进算法使用价值良好. 实际应用情况中, 检测条目越多, 将严重影响网络访问时延, 导致用户上网体验差; 检测条目越少, 匹配到的威胁少, 对网络安全危害增大, 一般检测条目约在500–800之间.

|
图 6 不同模式串集的算法性能 Fig. 6 Algorithm performance of different pattern |
本文也对改进算法在不同数据包时的情况, 模式串组使用Snort规则文件ftp.riles. 通过图7表示, 数据包越大, 改进算法所消耗时间短与原本算法, 能够提高其性能. 本文改进算法的测试平均查询时间为0.38 s, 传统算法需要2.16 s, 以此表示能够实现快速查询, 满足用户的实际使用需求.

|
图 7 不同数据包大小的算法性能 Fig. 7 Algorithm performance of different packet sizes |
通过实验结果表示, 改进之后的BM算法性能提高, 匹配效率比传统算法要高. 通过本文中的改进算法能够使入侵检测系统性能得到提高, 实用价值良好.
5 结束语网络带宽在网络技术持续发展过程中不断增加, 入侵监测系统处理的性能也要相应不断得到提高, 使得大流量网络环境的需求得到满足. 本文对模式匹配算法进行全面的研究, 并且对传统模式匹配算法进行改进. 通过实例测试可以看出来, 改进的多模式匹配算法能够有效满足网络使用过程中的需求, 并且提高系统检测效率. 另外, 改进算法还能够降低冗余移动, 使匹配速度与查找速率得到提高, 对入侵检测系统的性能进行改进.
| [1] |
于粉娟. 基于多模式匹配算法的计算机网络入侵检测研究. 自动化与仪器仪表, 2018, 15(5): 159-161. |
| [2] |
周小松, 刘帅. 多网络环境下的差异化入侵特征检测平台的设计与实现. 现代电子技术, 2017, 40(10): 149-152. |
| [3] |
吕峰, 叶东海, 杨宏, 等. 模糊数据挖掘和遗传算法的网络入侵检测方法. 电子技术与软件工程, 2017, 18(4): 185-186. |
| [4] |
Boyer RS, Moore JS. A fast string searching algorithm. Communications of the ACM, 1977, 10: 762–772.
|
| [5] |
刘达. 基于朴素贝叶斯分类算法的数据库入侵检测系统. 网络空间安全, 2017, 8(8-9): 32-34. |
| [6] |
Horspool NR. Practical fast searching in strings. Software Practice and Experience, 1980(6): 50–56.
|
| [7] |
关丽. 基于模式匹配的计算机网络入侵防御系统. 电子制作, 2019, 18(13): 81-82, 96. DOI:10.3969/j.issn.1006-5059.2019.13.032 |
| [8] |
鲍海燕. 基于K-means算法的入侵检测系统研究. 现代计算机, 2019, 19(23): 9-13. DOI:10.3969/j.issn.1007-1423.2019.23.002 |
| [9] |
朱平哲. 网络入侵检测与防护算法系统的实现. 安徽电子信息职业技术学院学报, 2019, 18(3): 7-12. DOI:10.3969/j.issn.1671-802X.2019.03.002 |
| [10] |
常刚, 罗作民. 基于聚类算法的入侵检测系统设计. 自动化与仪器仪表, 2018, 15(9): 110-113. |
| [11] |
吴志福. 基于一次判断双字符比较的模式匹配算法. 科技通报, 2018, 34(4): 240-242, 261. |
| [12] |
刘建. 基于改进神经网络的网络入侵检测. 科技创新与应用, 2018, 16(2): 11-12, 14. |
| [13] |
Chen JL, Li QY, Li JQ, et al. DOA estimation of MIMO Radar based on covariance matching SL0 algorithm. Radar Science and Technology, 2019, 17(1): 19-24. |
| [14] |
王子玲, 贾舒宜, 修建娟, 等. 基于人工神经网络的多模型目标跟踪算法. 海军航空工程学院学报, 2019, 34(4): 343-348. |
 2021, Vol. 30
2021, Vol. 30


