传统的协同过滤推荐算法[1]通过分析相似用户的偏好来得到对目标用户的推荐结果, 这种方式尽管有效, 但还是不够可靠[2]. 心理学研究表明, 在现实生活中, 人们倾向于向专家咨询, 听取专家的意见. 据此, 国内外大量学者提出了改进办法. 国外学者Kardan等[3]首次建议利用专家用户进行推荐, 但计算专家信任度值的方法不成熟导致专家用户的选取不是很准确. Hwang等[4]充分考虑进用户的行为数据, 在基于用户的协同过滤推荐算法中加入了信任因素, 降低了推荐误差. 国内学者王孝先[5]利用了一小部分专家数据集噪声很低的优势为庞大的用户集合做预测评分, 避免了数据稀疏性为推荐质量带来的不利影响, 但未考虑日常用户愿意参考有相似兴趣的朋友的意见的心理; 贾彭慧等[6]通过计算用户之间的交叉性、信任性、趋同性和专家因子动态地为每个用户挖掘出特定的专家数据集, 使专家的选取更具有针对性, 但该算法一味地信任专家而忽略了相似用户的意见, 且在计算上无法同时为目标用户选取相似用户.
可以看出, 尽管上述算法在一定程度上提高了推荐的准确性, 但是仍存在需要改进的地方. 首先, 在为目标用户寻找相似用户时, 传统的协同过滤推荐算法在相似度计算上忽略了用户活跃度偏差问题. 改进算法考虑到“用户活跃度”和“活跃度差异”对相似度的影响, 设置活跃度阈值, 对大于阈值的活跃用户设计惩罚权重, 降低其对用户间相似度的贡献, 使选取出的相似用户与目标用户的喜好更为接近. 与此同时, 鉴于现有的专家信任度值计算公式不能充分处理来自不同项目的数据信息的情况, 例如, 有些用户更擅长给喜剧电影打分, 有些更擅长给动作电影打分, 用户的专家信任度值随着项目的不同也在发生变化, 改进算法在专家信任度计算公式中加入项目平衡因子, 使用户的专家信任度值随着推荐项目的不同而变化. 最后, 通过改进的DBSCAN算法根据兴趣和爱好的相似性[7, 8]将用户划分到不同的社区簇中[9], 只需在各社区簇内寻找专家用户和相似用户, 大大缩小了计算范围, 提高了算法的推荐效率与推荐质量.
1 基本原理 1.1 基于用户的协同过滤推荐算法基于用户的协同过滤推荐算法UCF (User Collaborative Filtering)通过计算相似度以找到一组与目标用户喜好相似的用户[10], 并通过分析相似用户的偏好来预测目标用户的偏好[11,12]. 整个过程如图1所示.

|
图 1 协同过滤推荐过程 |
在协同过滤推荐系统中, 相似度计算是指计算各用户之间的相似度. 当前使用最广泛的相似度计算方法主要包括Pearson相关系数和Jaccard相关系数[13].
Pearson相关系数的结果是通过目标用户x和其相似用户y共同得分的项目集计算得出的. 计算式如式(1)所示.
| $ S{{im}}(x,y) = \frac{{\displaystyle\sum\limits_{i \in I_{x,y}} {\left( {R_{xi} - \overline {R_{x}} } \right)\left( {R_{yi} - \overline {R_{y}} } \right)} }}{{\sqrt {\displaystyle\sum\limits_{i \in I_{x,y}} {{{(R_{xi} - R_{x})}^2}} } \sqrt {\displaystyle\sum\limits_{i \in I_{x,y}} {{{(R_{yi} - R_{y})}^2}} } }} $ | (1) |
式中, Sim (x, y)表示用户x和y之间的相似度, Rxi和Ryi分别代表用户x和y对项目i的评分, Ixy代表用户x和y共同评分的项目集合,
Jaccard相关系数结果是通过计算集合中样本交集数量与样本并集数量之比得出的, 计算式如式(2)所示.
| $ S{{im}}(x,y) = \frac{{\left| {N_x \cap N_y} \right|}}{{\left| {N_x \cup N_y} \right|}} $ | (2) |
式中, Nx和Ny分别代表用户x和y评分的项目列表,
按照与目标用户相似度值的大小选取相似用户集, 为目标用户生成Top-N推荐列表. 评分预测公式如式(3)所示:
| $ {{p}}_{xi}=\overline{R_{x}}+\frac{{\displaystyle \sum _{y\in N}Sim(x,y)\cdot \left( {R_{{y,i}}-\overline{{R_{y}}}} \right)}}{{\displaystyle \sum _{y\in N}\left|Sim(x,y)\right|}} $ | (3) |
式中, pxi表示用户x对项目i的预测评分, Sim(x, y)代表用户x和y之间的相似度.
1.2 基于专家信任的协同过滤推荐算法基于专家信任的协同过滤推荐算法EPT (Expert Prior Trust recommend)将专家信任因素引入到协同过滤算法中来, 专家信任度表明了用户在特定情境中拥有知识、能力、技巧的可信度. 在协同过滤推荐系统中, 某用户评过分的项目数越多, 且评分的准确度越高, 该用户的专家信任度值就越高. 已有的专家信任度值计算公式如式(4)所示:
| $ {{trust}}(x) = \frac{1}{{M_{\max }}} \times \sum\limits_{i = 1}^{{m}} {\left\{ {1 - \frac{{\left| {R_{x,i} - \overline {R_i} } \right|}}{{\mathop R\nolimits_{\max }^i }}} \right\}} $ | (4) |
式中, trust(x)表示用户x的专家信任度值, Mmax代表评分最多的用户的评分数量, m代表评分矩阵中项目总数,
传统的协同过滤推荐算法未考虑用户活跃度偏差对相似度计算的影响, 且已有的基于专家信任的协同过滤推荐算法[14]未考虑项目之间的差异对专家信任度值带来的影响. 为有效解决以上问题, 本文提出一种融合专家信任的协同过滤推荐算法CFRAIETS (Collaborative Filtering Recommendation Algorithm based on Improved Expert Trust and Similarity). CFRAIETS主要作了两部分改进, 下面详细介绍CFRAIETS算法的内容.
2.1 相似度计算改进Pearson相关系数通过计算两用户的共同评分项目来得到相似度值, 但忽视了用户间共同评分项目所占比例问题[15], 不适用于非常稀疏的数据集; Jaccard 相关系数仅关注用户是否对该项目评过分, 适用于稀疏度高的数据集合, 但未考虑用户对项目的评分取值. 因此在改进相似度计算的时候, 首先综合Jaccard 相关系数和加权后的Pearson相关系数, 有效结合两种算法的优点. Pearson相关系数的加权系数Weight(x, y)公式如式(5)所示.
| $ W{{eight}}(x,y) = \sqrt {\frac{{\displaystyle\sum\limits_{{{i}} \in I_{x,y}} {R_{x,i}} }}{{\displaystyle\sum\limits_{i \in I_x} {R_{x}} }}} \times \sqrt {\frac{{\displaystyle\sum\limits_{{{i}} \in I_{x,y}} {R_{y,i}} }}{{\displaystyle\sum\limits_{i \in I_y} {R_{y}} }}} $ | (5) |
传统的协同过滤推荐算法在计算相似度时忽略了用户活跃度偏差带来的影响, 导致活跃用户间的相似度偏高. 本文算法在改进时涉及到了“用户活跃度” 和“活跃度差异”两个概念. “用户活跃度”在这里是指用户评过分的项目数, 某用户评价过的项目数越多, 该用户的活跃度就越高. 对给定的两用户, 若活跃度都很高, 那么这两位用户之间的相似度将在一定程度上受到用户自身活跃度的影响, 并不代表他们一定有多么相似; 相反, 若两用户的活跃度比较低, 但是却都对一定数量的项目采取过近似的评分, 那么可能代表着他们的兴趣较为相似. 对每个用户x, 其评价过的项目数为Numxi, 用户x的活跃度为: ActUserx=Numxi, 对其进行归一化, 使用户活跃度取值保持在[0, 1]之间. 归一化公式如式(6)所示.
| $ N{{orm}}ActUser_x = \frac{{ActUser_x{{ - MinAct}}}}{{{{MaxAct - MinAct}}}} $ | (6) |
式中, NormActUserx表示归一化后的用户活跃度, MaxAct和MinAct分别代表用户活跃度的最大值和最小值.
“活跃度差异”是指归一化后用户活跃度之差的绝对值. 活跃度差异越小的活跃用户间的共同评分项可能越多. 计算公式如式(7)所示.
| $ A{{ct}}Bias_{x,y} = \left| {NormActUser_{x} - NormActUser_{y}} \right| $ | (7) |
分析“用户活跃度”和“活跃度差异”对相似用户选取时的影响, 活跃用户对相似度的贡献应该小于不活跃的用户, 需要对其设计相似度惩罚函数, 降低活跃用户间的相似度以缓解传统相似度量方法中存在的不足, 使用户间的相似度更为准确. 活跃度越高的用户对相似度的贡献越小, 反之则对相似度贡献越大. 因此“用户活跃度”与惩罚权重正相关. 而活跃用户间的“用户活跃度差异”越小, 他们共同评价过的项目可能就越多, 相似度惩罚权重就应越大, 因此“活跃度差异”与惩罚权重负相关. 结合以上分析, 引入惩罚权重式如式(8)和式(9)所示.
| $ \omega _x\;\;\left\{ {\begin{array}{*{20}{c}} {\rm{1}}&{{{NormActUser_x}} < \mu }\\ {\dfrac{{{{NormActUser_x}}}}{{{{ActBias_{x,y}}}}}}&{{{NormActUser_x}} \ge \mu } \end{array}} \right. $ | (8) |
| $ \omega _y\;\;\left\{ {\begin{array}{*{20}{c}} {\rm{1}}&{{{NormActUser_y}} < \mu }\\ {\dfrac{{{{NormActUser_y}}}}{{{{ActBias_{x,y}}}}}}&{{{NormActUser_y}} \ge \mu } \end{array}} \right. $ | (9) |
式中, ωx和ωy表示用户x和用户y的惩罚函数, 反映了活跃度有差异的两个用户在计算相似度时体现的不同权重, μ代表设定的活跃度阈值. 如果用户x或y的活跃度小于该阈值, 认为该用户的活跃度较低, 惩罚权重设为1; 若大于该阈值, 则认为用户的活跃度较高, 活跃度较高的用户间活跃度差异越小, 惩罚权重就越大.
综合式(1)(2)(5)(8)(9), 得出改进的相似度计算公式如式(10)所示.
| $ \begin{split} S{{im}}(x,y) =& \frac{{\displaystyle\sum\limits_{i \in I_{x,y}} {\left[ {\left( {R_{xi} - \overline {R_{x}} } \right)\omega _x} \right]\left[ {\left( {R_{yi} - \overline {R_{y}} } \right)\omega _y} \right]} }}{{\sqrt {\displaystyle\sum\limits_{i \in I_{x,y}} {{{\left[ {\left( {R_{xi} - \overline {R_{x}} } \right)\omega _x} \right]}^2}} } \sqrt {\displaystyle\sum\limits_{i \in I_{x,y}} {{{\left[ {\left( {R_{yi} - \overline {R_{y}} } \right)\omega _y} \right]}^2}} } }} \\ & \cdot weight(x,y) \cdot \dfrac{{\left| {N_x \cap N_y} \right|}}{{\left| {N_x \cup N_y} \right|}} \end{split} $ | (10) |
已有的专家信任度公式在计算用户的专家信任度值时, 将所有推荐项目都一视同仁[16], 未考虑项目间的差异. 例如项目i为恐怖电影, 项目j为爱情电影, 用户x喜欢看恐怖类型的电影, 不喜欢看爱情类型的电影, 因此恐怖电影应该是用户x擅长打分的类型, 而爱情电影是该用户不擅长打分的类型, 这导致其对恐怖电影的打分会较为准确, 而对爱情电影的打分就不那么准确了. 该用户对项目i的信任度值应高于对项目j的信任度值. 由此看出, 对于不同的项目, 用户的专家信任度值并不应该是静态的, 若是在计算时不将项目间的差异考虑在内, 会大大降低推荐结果的准确性. 项目间的差异来自于各项目从属的不同类型, 而类型是项目的固有属性, 无法直接将其引入到计算中来, 但是可以把类型差异体现在各项目与其所属用户评分矩阵中所有其他项目之间的相似度大小上. 可以理解为项目之间的相似度越高, 他们的属性就越相近.
对此, 本文提出一种使用项目平衡因子来改进现有专家信任度值的方法. 计算用户x对项目i的专家信任度, 首先计算推荐项目i与用户所有项目间的相似度, 假如项目i与用户x评价过的大多数项目的相似度都高, 说明项目i是用户擅长的类型, 那么用户x对项目i的专家信任度就越高. 反之, 项目j与用户x评价过的大多数项目的相似度都较低, 说明要被推荐的项目j不是用户擅长的评分类型, 则用户x对项目j的专家信任度较低.
加入项目平衡因子后的专家信任度值计算公式如式(11)所示.
| $ trust{(x)^i} = \frac{1}{{M_{\max }}} \times \sum\limits_{j = 1}^{\rm{m}} {\left[ {1 - \frac{{\left| {R_{x,j} - \overline {R_j} } \right|}}{{\mathop R\nolimits_{\max }^j }}} \right]} \cdot I_{trust(i,j)} $ | (11) |
其中:
| $ I_{{{trust}}({{i}},j)} = \frac{{\displaystyle\sum\limits_{{{x}} = 1}^{{n}} {\left( {R_{x,i} - \overline {R_i} } \right)\left( {R_{x,j} - \overline {R_j} } \right)} }}{{\sqrt {\displaystyle\sum\limits_{x = 1}^n {{{\left( {R_{x,i} - \overline {R_i} } \right)}^2}} } \sqrt {\displaystyle\sum\limits_{x = 1}^n {{{\left( {R_{x,{{j}}} - \overline {R_j} } \right)}^2}} } }} $ | (12) |
式中, Itrust(i,j)表示项目平衡因子, Rx,i、Rx,j代表用户x对项目i、项目j的评价分数,
和传统的专家信任度计算方法不同的是, 改进算法将项目平衡因子作为权值对用户评价过的项目集合进行了加权处理, 项目平衡因子的计算方法根据项目矩阵的情况使用了Pearson计算方法, 但与选取相似用户时的Pearson方法的变量大不相同, 不能混淆. 式(11)中的m是指去掉项目i后的用户评分矩阵中的项目数, 在对这m个项目进行处理和求和时, 可以同时计算出第i个项目与这m个项目之间的相似度, 因此直接在专家信任度计算公式中加入项目平衡因子的做法是切实可行的.
2.3 改进后的评分预测公式为提高系统性能, 缓解严重的数据稀疏性问题, 本文按照参考文献[8]将用户按照兴趣爱好的相似性聚类到了不同的社区簇中. 再将改进后的相似度与专家信任度因素融合在一起考虑, 对评分预测公式进行改进. 改进后的评分预测公式如式(13)所示:
| $ \begin{array}{l} P_{x,i} = \overline {R_{x}} + \\ \frac{{\alpha \displaystyle\sum\limits_{a_1}^{k_1} {trus{t^i}(a_1)\times\left( {R_{a_1,i}-\overline {R_{a_1}} } \right)+\beta \sum\limits_{a_2}^{k_2} {\left| {sim(a_2,x)} \right|\times\left( {R_{a_2,i}-\overline {R_{{{a}}_2}} } \right)} } }}{{\alpha \displaystyle\sum\limits_{{{a_1}}}^{k_1} {trus{t^i}(a_1) + \beta \displaystyle\sum\limits_{a_2}^{k_2} {\left| {sim(a_2,x)} \right|} } }} \end{array} $ | (13) |
式中, Px,i表示用户x对物品i的预测评分,
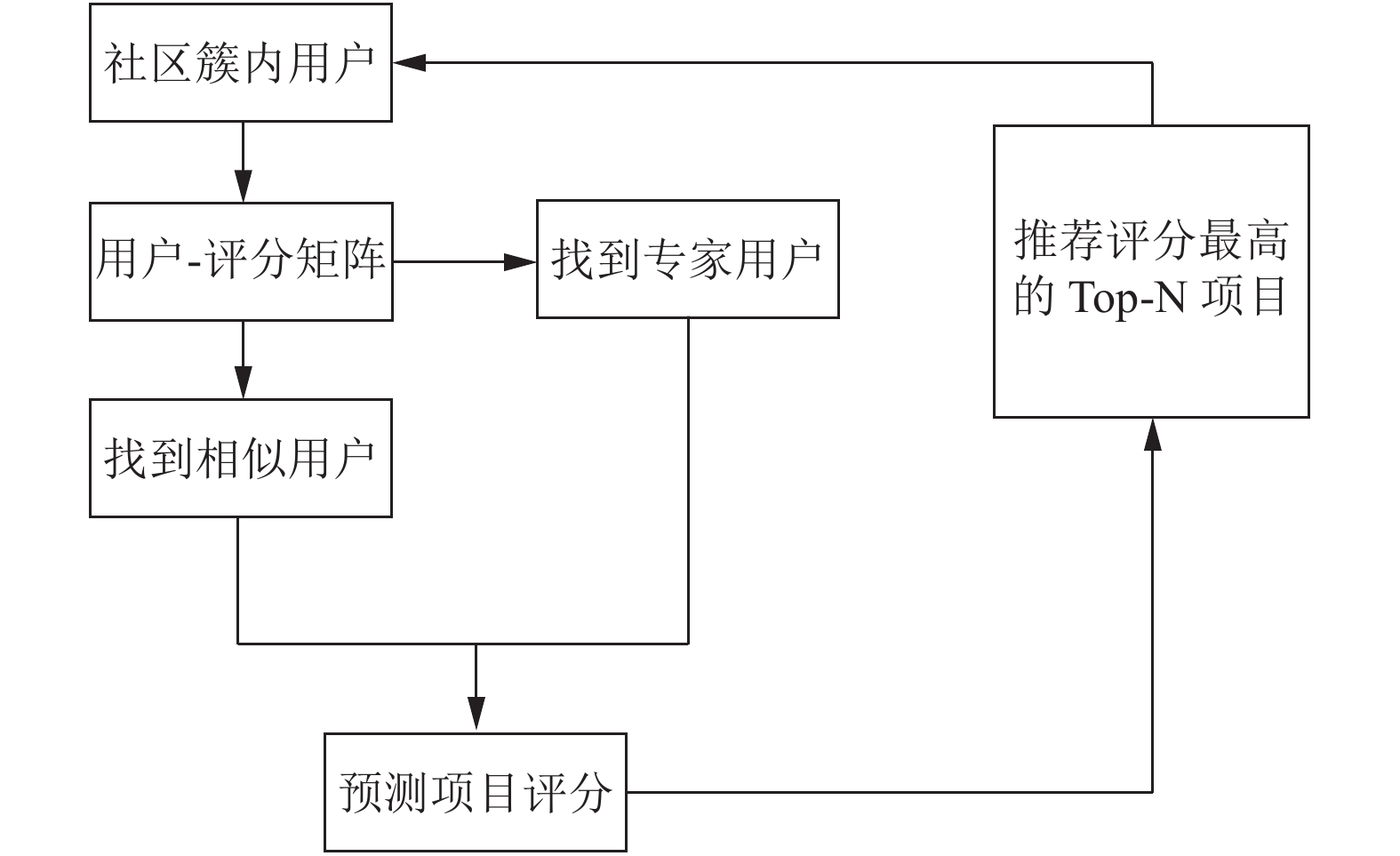
|
图 2 融合专家信任的协同过滤推荐过程 |
本文算法的推荐过程具体如下:
输入: 社区簇内目标用户x, 用户-评分矩阵H, 推荐项目数N.
输出: 为目标用户x推荐的N个结果.
步骤1. 将用户按照兴趣爱好的不同进行聚类, 确定社区簇的数量K.
步骤2. 引入惩罚权重式, 根据式(10)计算各社区簇中用户之间的相似度, 确定目标用户的相似用户集合U1.
步骤3. 在社区簇内寻找专家用户, 确定专家用户集合U2, 并根据式(11)计算专家用户对其评价过的每个项目的专家信任度值.
步骤4. 确定各社区簇内专家用户和相似用户所占的比例, 确定专家用户的个数k1和相似用户的个数k2, 确定评分预测公式中的权重平衡因子α和β.
步骤5. 根据式(13), 通过专家用户和相似用户, 为目标用户推荐N部其可能喜欢的电影.
当新用户到来时, 利用具有权威性的专家用户对其进行推荐. 冷启动下的评分预测公式如式(14)所示.
| $ p_{x,{{i}}} = \frac{{\displaystyle\sum\limits_{j = 1}^n {trus{t^{{i}}}} (u_j) \times R_{uj,i}}}{{\displaystyle\sum\limits_{j = 1}^n {trus{t^{{i}}}} (u_j)}} $ | (14) |
式中, px,i表示用户x对项目i的预测评分, n代表社区簇内的专家数量, trusti(uj)代表第j个专家对项目i的信任值.
3 实验设计 3.1 实验设置实验采用由美国GroupLens研究小组创办的MovieLens公共数据集, 随机将80%划分为训练集, 将剩余的20%划分为测试集, 数据稀疏性为0.937. 该数据集中共包含943个用户对1682部电影的100000个评分, 评分区间为1-5, 用户的喜好可以用评分值大小来衡量, 每位用户评价过的电影数均超过20部.
本实验采取平均绝对误差(MAE)和准确率(Precision)作为评价指标. MAE是系统正确预测用户对每个物品偏好的能力时最常用的方法, 它计算推荐得分与实际得分值的平均偏差. Precision分类衡量标准用来衡量命中物品数占推荐物品总数的比例.
3.2 实验过程分析(1)分析电影类型, 确定社区簇的数量为7.
MovieLens数据集中共包含19种电影类型, 考虑到可以将类型相近的影片归到一个大类中[17], 例如可以将Animation(卡通)和Children’s(儿童)视为一类, 将Crime(犯罪)、Horror(恐怖)和Thriller(惊险)视为一类, 将分别喜欢这些影片的用户划分到一个社区簇内. 通过分析影片类型, 初步确定社区簇的数量应在4–8个之间. 再通过实验, 调整用户聚类数比较平均绝对误差MAE的大小. 随着社区簇个数的变化, MAE值的变化如图3所示.

|
图 3 随划分社区簇个数改变的MAE值 |
在社区簇个数为7时, MAE值最小. 因此确定社区簇的数量为7.
(2)引入惩罚权重式改进相似度计算, 确定活跃度阈值μ为200.
分析数据集中943名用户评过分的电影数, 看过的电影数目小于100部, 即用户活跃度小于100的用户共655人, 占总体用户的69.459%(655/943), 看过的电影数目在100–200之间的用户占总体用户的20.148%(190/943), 用户活跃度在200–300之间的用户占总体用户的7.423%(70/943), 剩余用户仅占2.969%(28/943), 用户活跃度较高的用户占用户总数的小部分. 将用户活跃度阈值μ在100–500之间调试, 在阈值的取值超过200后, 该惩罚权重对相似度的贡献基本不再发生变化且在200时MAE值最小. 因此用户活跃度阈值μ确定为200.
(3)确定社区簇内相似用户的数量为15, 专家用户所占的比例为17%, 评分预测公式中权重评分因子α为0.4, β为0.6.
在改进了相似度的协同过滤推荐算法中融合进专家信任因素, 在该步骤, 首先确定相似用户数量K, 分别取5、10、15、20、25、30、35, 取值为15时, 同时兼顾了较好的MAE值和Precision值, 因此将相似用户数量确定为15.
接下来确定专家用户在社区簇中的比例, 采用的方法是根据各个社区簇内每个用户的专家信任度值进行大小排序, 取前ω%的用户作为该社区簇内的专家用户. ω%从8%~20%中取值, 同时权重系数α从0.3、0.4、0.5、0.6、0.7中取值, 观察MAE值的变化如图4所示.

|
图 4 权重系数α和专家数量百分比对MAE值的影响 |
由此可以看出, 随着社区簇中专家用户比例的增加和评分公式中专家用户权重系数的增加, MAE值逐渐减小, 但推荐精度也不会一味随着专家数量的增多而提高, 因为本来也只有小部分用户才能被称之为专家, 专家用户数量一旦过高, 不仅会导致挑选出的一部分专家不够专业, 也会导致目标用户一味地相信专家而忽略与其爱好相近的相似用户的意见, 从而导致推荐效果不是太理想. 因此, 在专家用户数量所占社区簇的比例为17%, 权重系数α取0.4,β取0.6时, MAE值最低, 推荐效果最佳, 且更为均衡地考虑到了两类用户的意见.
3.3 实验结果分析为验证本文两个创新点有效, 共设计了5组实验. 引入传统的基于用户的协同过滤推荐算法UCF (User Collaborative Filtering)[18]和基于用户聚类的协同过滤算法UCFC (User Collaborative Filtering based on Clustering)[19]用来侧重于验证对于相似度计算部分的改进有效. 引入文献[5]中的基于专家信任的协同过滤推荐算法EPT (Expert Prior Trust recommend)和基于专家信任的用户聚类协同过滤推荐算法UCCFRET (User Clustering Collaborative Filtering Recommendation based on Expert Trust)[20]用来侧重于验证对于专家信任度计算部分的改进有效. 其中, UCCFRET是本文作者已发表论文《基于专家信任的协同过滤推荐算法改进研究》中设计的算法, 本文算法与该算法最大的不同是, 本文在相似度计算上和专家信任度计算上做了进一步改进研究. 将以上4种算法和本文融合专家信任的协同过滤推荐算法CFRAIETS进行对比试验.
经实验验证, 本文算法CFRAIETS的MAE值最低, Precision值最高. 对比算法在不同相似用户数目K下的MAE值如表1所示, MAE值变化情况如图5所示.
| 表 1 算法在不同相似用户数目下的MAE值 |
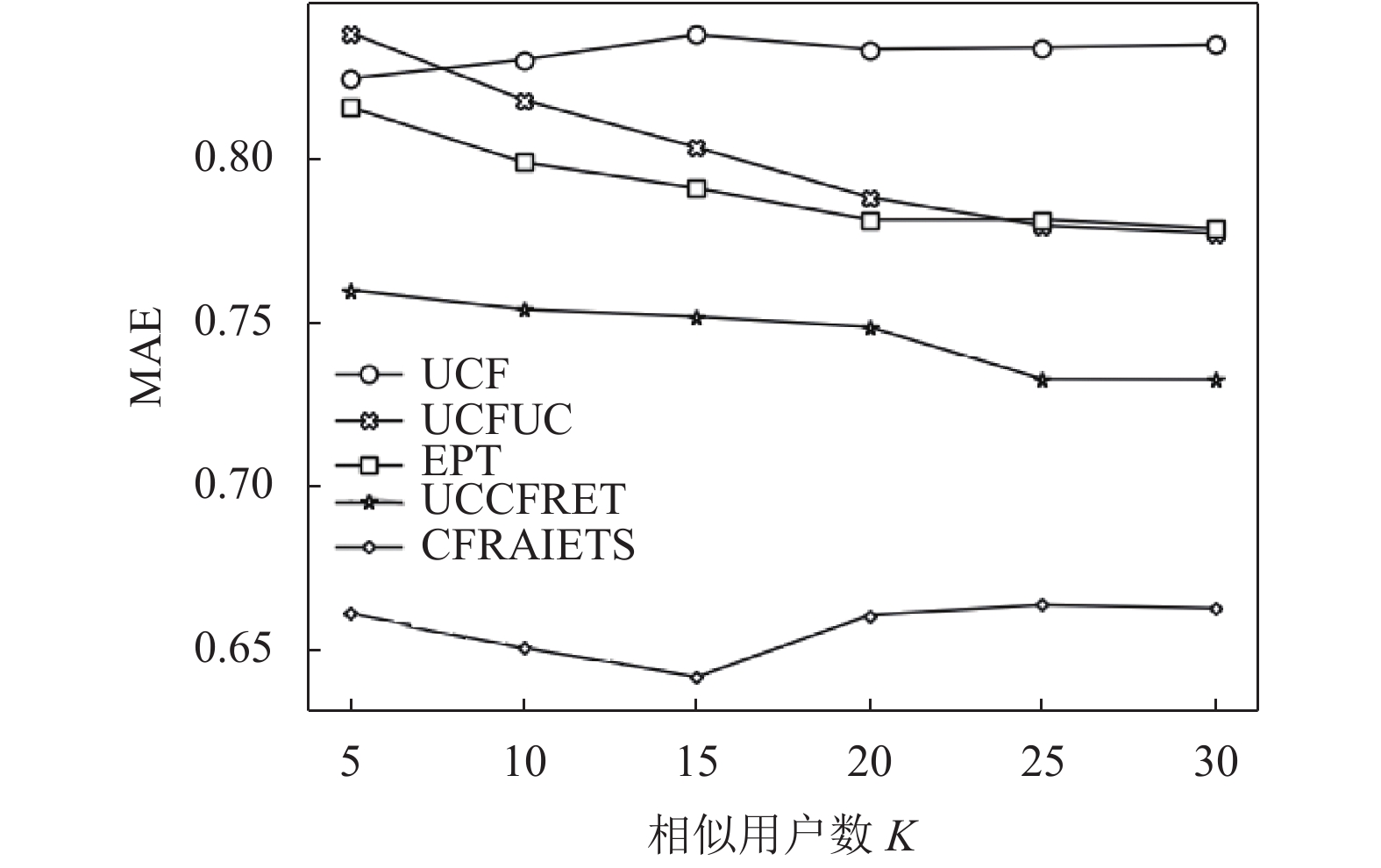
|
图 5 算法在不同相似用户数目下的MAE值变化 |
对比算法在不同相似用户数目下的Precision值如表2所示, Precision值变化情况如图6所示.
| 表 2 算法在不同相似用户数目下的Precision值 |
综合图5图6可以看出, 改进了相似度计算的CFRAIETS对用户偏好的预测能力有明显提高, 且在预测准确率上也有了显著改善. 加入了专家信任因素的算法随着近邻用户的增加, MAE值逐步减小后又增大, Precision值逐步增加后大致走向趋于平缓, 在近邻用户达到一定数目后, 近邻用户对推荐准确度的贡献就没有那么高了, 这是因为只有小部分相似用户与目标用户的兴趣爱好最为相近, 在相似用户超过了一定数目之后, 再加入推荐的就是与目标用户没那么相似的用户了, 这时, 专家用户的客观评价对推荐的准确度就显得尤为重要了. 综上, 本文提出的融合专家信任的协同过滤推荐算法CFRAIETS在一定程度上均优于其他算法, 显著提高了推荐能力.

|
图 6 算法在不同相似用户数目下的Precision值变化 |
4 结语
针对传统协同过滤推荐算法的一系列问题, 考虑到人们在现实生活中普遍信任专业人士的因素及考虑到优秀的推荐算法不仅可以准确预测用户的需求, 还可以帮助用户发掘长尾商品, 决定利用专家信任和相似度结合的优势, 提出一种融合专家信任的协同过滤推荐算法, 并在公开数据集MovieLens上进行了离线模拟实验. 首先确定社区簇数量, 在相似度计算上为活跃用户设计相似度惩罚函数, 并确定惩罚权重式中的阈值, 接下来在专家信任度计算公式中加入项目平衡因子进行改进, 得到专家用户对其评价过的每一部电影的信任度值, 再确定社区簇中相似用户的最优数量及专家用户的比例、确定评分预测公式中权重平衡因子的最优取值, 最后设计对比算法并分析实验结果. 实验结果最终表明本文的融合专家信任的协同过滤推荐算法不仅丰富了推荐的多样性, 还显著提高了推荐系统的推荐质量和准确度. 但是本文算法仍然有一定的局限性, 首先, 因受条件限制, 只在MovieLens数据集上进行了离线实验. 其次, 在本文作者已发表的论文[20]中, 算法UCCFRIE考虑到了异社区簇的概念, 本文算法也应在此基础上进一步考虑如何将改进部分应用到异社区簇中. 最后, 本文在专家信任度值计算改进的过程中对项目因子的考虑目前还不够成熟, 在今后的研究和实践中, 将更加深入地对这些问题进行思考和改进, 并在多个数据集上进行测试, 在实际的推荐系统中进行在线实验, 不断优化该算法的可拓展性及复杂度.
| [1] |
刘君良, 李晓光. 个性化推荐系统技术进展. 计算机科学, 2020, 47(7): 47-55. |
| [2] |
Qian FL, Yue RX, Zhao S, et al. Robust recommendation algorithm using an iterative group-based reputation. Proceedings of the 2018 IEEE 3rd International Conference on Cloud Computing and Big Data Analysis. Chengdu, China. 2018. 62–70.
|
| [3] |
Kardan AA, Aziz M, Shahpasand M. Adaptive systems: A content analysis on technical side for e-learning environments. Artificial Intelligence Review, 2015, 44(3): 365-391. DOI:10.1007/s10462-015-9430-1 |
| [4] |
Hwang WS, Lee HJ, Kim SW, et al. Efficient recommendation methods using category experts for a large dataset. Information Fusion, 2016, 28: 75-82. DOI:10.1016/j.inffus.2015.07.005 |
| [5] |
王孝先. 基于专家用户的协同过滤推荐算法研究[硕士学位论文]. 秦皇岛: 燕山大学, 2015.
|
| [6] |
贾彭慧, 刘鑫一, 孔亚斌, 等. 基于专家动态生成的协同过滤推荐算法. 计算机技术与发展, 2020, 30(3): 19-23. DOI:10.3969/j.issn.1673-629X.2020.03.004 |
| [7] |
申晋祥, 鲍美英. 基于用户聚类与项目划分的优化推荐算法. 计算机系统应用, 2019, 28(6): 159-164. DOI:10.15888/j.cnki.csa.006950 |
| [8] |
孟晗, 高岑, 王嵩, 等. 结合信任关系的用户聚类协同过滤推荐算法. 计算机系统应用, 2020, 29(8): 224-229. DOI:10.15888/j.cnki.csa.007561 |
| [9] |
张凯涵, 梁吉业, 赵兴旺, 等. 一种基于社区专家信息的协同过滤推荐算法. 计算机研究与发展, 2018, 55(5): 968-976. DOI:10.7544/issn1000-1239.2018.20170253 |
| [10] |
李龙生, 艾均, 苏湛, 等. 结合用户行为和物品标签的协同过滤推荐算法. 计算机应用与软件, 2018, 35(6): 248-253. DOI:10.3969/j.issn.1000-386x.2018.06.045 |
| [11] |
Chen CH, Karvela M, Sohbati M, et al. PERSON-personalized expert recommendation system for optimized nutrition. IEEE Transactions on Biomedical Circuits and Systems, 2018, 12(1): 151-160. DOI:10.1109/TBCAS.2017.2760504 |
| [12] |
Li C, Jiang ZT. A hybrid news recommendation algorithm based on user’s browsing path. Proceedings of the 2016 IEEE/ACIS 15th International Conference on Computer and Information Science. Okayama, Japan. 2016. 1–4.
|
| [13] |
王菲. 融合信任聚类的协同过滤算法研究与应用[硕士学位论文]. 南京: 南京邮电大学, 2019.
|
| [14] |
林建辉, 严宣辉, 黄波. 融合信任用户的协同过滤推荐算法. 计算机系统应用, 2017, 26(6): 124-130. DOI:10.15888/j.cnki.csa.005805 |
| [15] |
徐志超, 单剑锋. 基于改进型协同过滤算法的研究. 计算机技术与发展, 2019, 29(10): 196-200. DOI:10.3969/j.issn.1673-629X.2019.10.038 |
| [16] |
李卫疆, 郑雅民. 基于信任关系和项目流行度的矩阵分解推荐算法. 计算机应用与软件, 2019, 36(9): 249-254, 275. DOI:10.3969/j.issn.1000-386x.2019.09.044 |
| [17] |
Jiang MY, Zhang ZF, Jiang JQ, et al. A collaborative filtering recommendation algorithm based on information theory and bi-clustering. Neural Computing and Applications, 2019, 31(12): 8279-8287. DOI:10.1007/s00521-018-3959-2 |
| [18] |
吴建帆, 曾昭平, 郑亮, 等. 基于用户的协同过滤推荐算法研究. 现代计算机, 2020(19): 27-29, 67. DOI:10.3969/j.issn.1007-1423.2020.19.006 |
| [19] |
刘璐, 王志谦. 一种改进的基于用户聚类的协同过滤推荐算法. 电视技术, 2018, 42(6): 1-4. |
| [20] |
刘国丽, 白晓霞, 廉孟杰, 等. 基于专家信任的协同过滤推荐算法改进研究. 计算机工程与科学, 2019, 41(10): 1846-1853. DOI:10.3969/j.issn.1007-130X.2019.10.018 |
 2021, Vol. 30
2021, Vol. 30


