各类APP依靠互联网扩大影响, 为提高自身在同行业中的竞争优势, 采用传统用户分类模型, 对注册用户进行分类以便提供更好的服务. 互联网具有强大的通讯和社交功能, 互联网企业以互联网为依托, 开发具有企业特色的APP软件, 吸引使用者利用APP浏览网上信息. 但随着信息化时代到来, 企业发现互联网带来的丰厚利益, 越来越多的企业投身到互联网行业中, 竞争变得越来越激烈, 因此为了提高自身的竞争优势, 提出利用一种分类手段, 将网站中的互联网用户进行分类, 相关学者对此进行了仔细研究. 欧阳晔等^[1]提出一个基于机器学习算法的分类模型, 旨在利用该算法, 对网络用户浏览偏好进行分类; 王嘉祺等^[2]提出用户分类系统在不同的社交网络中发挥着重要的作用, 例如恶意账号检测, 高影响力用户发现及会员用户发现. 引入深度学习技术来解决用户分类问题, 且使用了陌陌的真实数据进行评估, 对于不同的分类目标,均可取得较好的效果, 但是分类准确度较低; 蒲杰方, 卢荧玲^[3]筛选了14个关键变量作为影响客户是否购买定期存款的影响因素, 并对重要特征进行初步分析; 根据数据特征利用k-means聚类算法对银行的客户群进行分类, 从而得出三类最有可能购买定期存款的客户群, 剖析每一类客户群的特征, 从而有针对性地为其提供差别化的分类, 但是分类用时较长. 这些传统模型的使用效果没有达到预期, 因此研究一个全新的互联网用户分类模型.

支持向量机简称为SVM, 是将风险控制在最小的一个机器学习算法, 通过SVM的计算, 得到全局最优解, 同时将计算难度降至最低, 减小以往学习算法的计算误差. 支持向量机解决了局部极小值的问题, 且具有较好的推广能力, 对于数据检测、数据挖掘以及数据处理等研究领域, 有不错的使用效果. 为进一步提高支持向量机的使用性能, 以原有支持向量机为依据, 对SVM改进, 得到全新的TWSVM和NPSVM. 改进后的SVM数据拟合性更好、求解数据的能力更强, 因此在互联网用户分类研究中, 引入改进的SVM进一步完善互联网用户分类方法.

1 基于改进SVM的互联网用户分类模型 1.1 构造样本数据

假设互联网用户浏览网络信息的时间序列为 $u\left( t \right)$ , 其中 $t \in \left( {1,N} \right)$ ; 令嵌入维数为 $n$ , 时间延迟为 $\lambda $ , 则 $N' = $ $ N - \left( {n - 1} \right)\lambda $ , 表示重构后的相空间矢量长度, 重构后获得 $n$ 维相空间相点 ${U_m}$ , $m \in \left( {1,N'} \right)$ , 表示 ${U_m}$ 的每一个分量都有 $n$ 个元素, 即维数^[4]. 以 $u\left( t \right)$ 中的 $u\left( m \right)$ 为起点, 每隔 $\lambda $ 个互联网用户信息, 重构相空间相点在相空间的轨迹, 公式为:

$\left\{ \begin{gathered} {U_1} = {\left( {{u_1},{u_{1 + \lambda }}, \cdots ,{u_{1 + \left( {n + 1} \right)\lambda }}} \right)^{\rm T}} \\ {U_2} = {\left( {{u_2},{u_{2 + \lambda }}, \cdots ,{u_{2 + \left( {n + 1} \right)\lambda }}} \right)^{\rm T}} \\ \vdots \\ {U_{N'}} = {\left( {{u_{N - \left( {n - 1} \right)\lambda }},{u_{N - \left( {n - 2} \right)\lambda }}, \cdots ,{u_N}} \right)^{\rm T}} \\ \end{gathered} \right.$

(1)

模型设置合适的嵌入维数, 则重构的相空间可以准确模拟互联网用户的浏览轨迹. 根据混沌理论可知, 嵌入维数 $n$ 的值太小, $c = 1,2,\cdots, n$ , 重构空间中的用户信息, 会因吸引子的作用, 而产生扭结和重叠现象, 此时的信息距离过于接近, 数据之间交融, 难以进行分类. 同时噪声的维数是无穷大的, 若嵌入维数 $n$ 的值太大则 $n - c$ 空间将被舍入误差完全覆盖, 因此在设置嵌入维数 $n$ 时, 采用误差最小算法设置嵌入维数^[5].

获得网络用户的时间序列数据 $\left\{ {{u_m}} \right\}_{m = 1}^M$ , 其中 ${u_m} = $ $ u\left( {{t_0} + m\Delta t} \right)$ , $M$ 表示样本数据个数; ${t_0}$ 表示用户浏览网页的初始时间; $\Delta t$ 表示样本时间间隔. 根据同样的假设条件, 则其在 $n$ 维空间 ${D^n}$ 中形成的新向量 ${U_m}$ 可被定义为:

$\left\{ \begin{array}{l} {U_m} = \left( {{u_m},{u_{m + 1}}, \cdots ,{u_{m + \left( {n - 1} \right)}}} \right) \\ m = 1,2, \cdots ,{N_n} \\ {N_n} = N - \left( {n - 1} \right)\lambda \\ \end{array} \right.$

(2)

根据式(2)的计算结果, 在 ${D^n}$ 中定义 ${U_i}$ 到 ${U_j}$ 的距离, 公式为:

$\left\| {{U_i} - {U_j}} \right\| = {\left\{ {\sum\limits_{t = 1}^{n - 1} {{{\left( {{u_{i + sr}} - {u_{j + sr}}} \right)}^2}} } \right\}^{1/2}}$

(3)

式中, $s$ 表示信息长度; $r$ 表示空间所占范围比^[6]. 根据嵌入定理, 令最佳延迟时间为 $\lambda $ , 则 $n$ 为最佳嵌入维数时的映射关系为 $f:D \to {D^n}$ , 其中 $f$ 表示关系参数, $D$ 表示网络空间中的用户信息. 则存在公式:

${N_{n + 1}} = f\left( {{N_n}} \right)$

(4)

利用映射 $f$ 的连续性, 当 ${U_i}$ 靠近 ${U_j}$ 时, ${u_{i + n}}$ 与 ${u_{j + n}}$ 之间也应靠近. 记 ${U_i}$ 的最邻近点是 $U_i^*$ , 则:

$\left\| {U_i^* - {U_i}} \right\| = \mathop {\min }\limits_{j = 1,2, \cdots ,{N_n}} \left\| {{U_j} - {U_i}} \right\|$

(5)

计算平均一步误差, 结果为:

$q\left( {n,\lambda } \right) = \frac{1}{{N - {N_n}}}\sum\limits_{i = 1}^{{N_n} - 1} {\left| {{u_{i + n}} - U_{i + n}^*} \right|} $

(6)

当 $n$ 比最佳嵌入维数小时, 误差 $q\left( {n,\lambda } \right)$ 较大; 当 $n$ 达到最小嵌入维数时, 因为映射 $f$ 所以 $q\left( {n,\lambda } \right)$ 减少. 当 $n$ 继续增大时, $q\left( {n,\lambda } \right)$ 随之变化, 当 $q\left( {n,\lambda } \right)$ 为最小时得到的最佳嵌入维数 $n$ , 可以作为最佳结果^[7]. 将该结果带入式(1), 重构的相空间可以反映互联网用户的浏览轨迹, 完成对样本数据的构造.

1.2 制定用户分类策略

根据互联网用户在浏览网页信息时浏览轨迹, 计算用户属性偏好度, 将分值作为用户分类的依据. 根据物联网客户的浏览轨迹, 设置用户标签, 包括: 财经、科技、数码、社交、交通、天气、新闻、法律、品牌、美食以及保险等. 利用数学算法, 计算用户浏览轨迹中, 存在的逻辑、类似偏好等, 从而形成分类定义^[8].

对第1.1节构造的样本进行统计, 合理转化统计结果拟合出函数图像, 根据图像中正负样本的差异指标重新清洗用户信息, 再次通过转化得到拟合函数图像, 若图中的样本数据分布分散, 说明提取的构造样本存在问题, 需要重新执行上述操作; 若函数分布差异性明显, 说明维度有效. 用户偏好B的变化控制样本在相空间的变化. 假设用户偏好存在 $w$ 个, 则有 ${B_1},{B_2},{B_3}, \cdots ,{B_w}$ , 数学算法的计算结果为:

${Z_i}\sim D\left( {{\tau _i},{\varphi ^2}} \right),i = 1,2, \cdots ,w$

(7)

式中, ${Z_i}$ 表示构造的样本数据集合; ${\tau _i}$ 表示受偏好 $B$ 变化影响的标签偏移阈值; $\varphi $ 表示偏好差异^[9]. 将显著性问题转化为偏好 $B$ 在 $D$ 空间内是否影响网页浏览选择行为, 即检验 ${G_0}:{\tau _1} = {\tau _2} = \cdots = {\tau _w}$ 是否成立. 给出下列方程, 其中各项参数为验证所需的指标.

$\left\{ {\begin{array}{*{20}{l}} {\bar {\textit{z}} = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^w {\sum\limits_{j = 1}^{{n_i}} {{{\textit{z}}_{ij}}} } }&\\ {S_1^2 = \displaystyle\sum\limits_{i = 1}^w {\displaystyle\sum\limits_{j = 1}^{{n_i}} {{{\left( {{{\textit{z}}_{ij}} - \bar {\textit{z}}} \right)}^2}} } } \\ {S_2^2 = \displaystyle\sum\limits_{i = 1}^w {\displaystyle\sum\limits_{j = 1}^{{n_i}} {{{\left( {{{\textit{z}}_{ij}} - {{\bar {\textit{z}}}_i}} \right)}^2}} } }&\\ {S_3^2 = \displaystyle\sum\limits_{i = 1}^w {\displaystyle\sum\limits_{j = 1}^{{n_i}} {{{\left( {{{\textit{z}}_i} - \bar {\textit{z}}} \right)}^2}} } } \end{array}} \right.$

(8)

上述公式中 $n$ 表示结果总数; $\bar {\textit{z}}$ 表示总均值; $S_1^2$ 表示总方差平方和; $S_2^2$ 表示组内平方和; $S_3^2$ 表示组间平方和^[10]. 根据上述指标, 得到 ${G_0}$ 的拒绝域为:

$V = \left\{ {\frac{{\left( {n - w} \right)S_3^2}}{{\left( {w - 1} \right)S_2^2}} > G\left( {w - 1,n - w} \right)} \right\}$

(9)

得到的检验结果可分为4种情况: 高度显著、显著、有一定影响、无显著影响, 根据该结果得到用户偏好B变化下对于互联网信息选择的影响程度建立一个互联网需求客户分类数据表, 如表1所示^[11].

按照上述分解结果, 制定一个详细的用户分类策略, 加强模型的分类效果.

1.3 基于改进的SVM设计分类模型

根据制定的分类策略, 利用改进的SVM设计分类模型对互联网用户进行分类. 用户的非线性可分情形下假设两个用户的选择向量分别为 $x$ 和 $y$ , 则经过改进SVM的非线性函数F的分类模型过程如下:

步骤1. 计算待分类样本与训练集之间的距离, 计算方法主要有欧氏距离;

步骤2. 按距离递增次序排序;

步骤3. 选取与当前点距离最小的 $k$ 个互联网用户;

步骤4. 统计前 $k$ 个互联网用户所在类别出现的频率;

步骤5. 返回前 $k$ 个互联网用户出现频率最高的类别作为互联网用户划分目标.

将用户选择向量映射到特征空间K内, 则两个向量的欧氏距离为:

${l^K}\left( {x,y} \right) = \sqrt {H\left( * \right) - 2H\left( {x,y} \right) + H\left( {y,y} \right)} $

(10)

式中, $H\left( * \right)$ 代表核函数^[12,13], 那么特征空间样本的中心向量 $C$ 为:

${C_F} = \frac{1}{n}\sum\limits_{i = 1}^n {F\left( {{x_i}} \right)} $

(11)

根据上述公式计算类中心, 再计算两类中心的距离, 公式为:

$ L = \left| {{C^ + } - {C^ - }} \right| $

(12)

式中, ${C^ + }$ 表示正类中心; ${C^ - }$ 表示负类中心. 计算两类样本与其他用户样本信息之间的距离, 当该距离小于公式(12)的计算结果时, 将样本作为有效候选支持向量, 即:

$ L' = \left| {{x_i} - C} \right| $

(13)

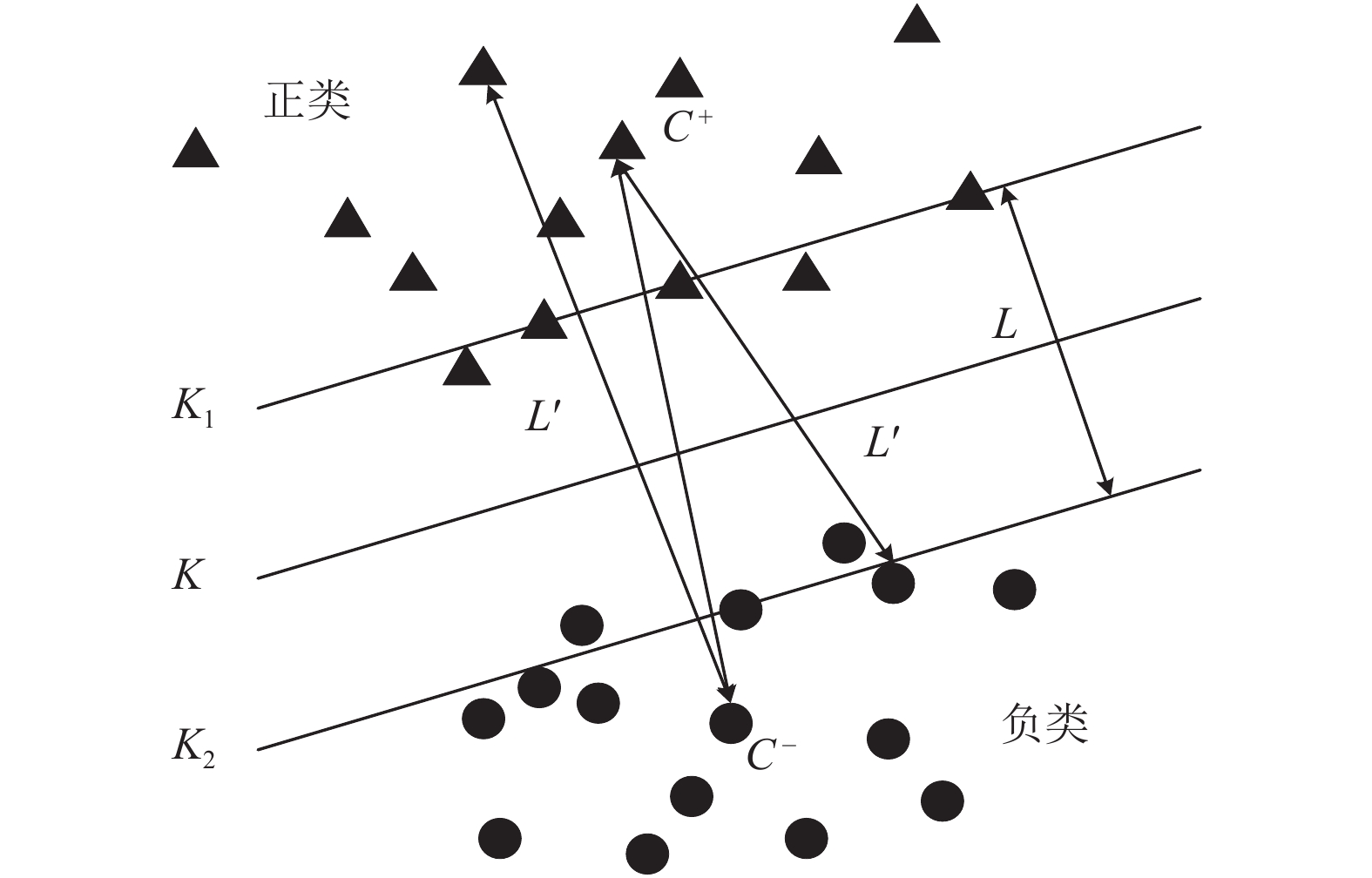
图1为保留满足 $L' < L$ 时, 样本作为有效候选支持向量的示意图^[14].

根据图1的示意图可知, 根据 $L'$ 和 $L$ 对特征空间中互联网用户选择进行划分, 以此将选择偏好相同的用户归集到一个数据集合中得到如表1所示的分类结果, 至此实现基于改进SVM的互联网用户分类^[15].

2 实验研究 2.1 性能测试

以互联网上某一期间的新闻作为实验测试基本条件, 利用设计的分类模型分别统计该期间的新闻展现量 $P$ 和点击量 ${\rm{click}}$ , 其中得到的新闻展现量统计分析结果如表2所示.

表2中, 展现次数为浏览过某条新闻的用户数量. 已知此次展现次数的最小值为1, 最大值为645, 均值为11, 其中展现次数为50的新闻, 所占比例为0.0009, 表1是20次以内展现次数的统计结果. 根据表中数据可知, 展现次数小于10的累积分布率约为78.06%, 展现次数小于20的累积分布率约为89.42%. 分类模型取新闻展现量P的对数, 得到下图2所示的新闻展现量P的分布图.

根据图中显示数据可知, 得到的分布是一个长尾的幂律分布, 大部分点集中分布在较小展现量处. 新闻作为网民了解国情、社会事件的重要媒介, 更新速度十分迅速. 用户根据自身偏好, 只浏览自身感兴趣的新闻类型. 因此该模型推断出大量用户浏览新闻的时间较为零散, 专门定点浏览新闻的用户数量较少. 因此该分类模型根据这一分析, 以用户偏好作为参考进行互联网用户分类. 为了实验测试的严谨性, 对该模型进行3次性能测试, 并计算该分类模型的分类准确率, 当该模型的分类准确率在95%以上时, 证明该模型成立且具有使用价值. 表3为模型分类准确性计算结果.

根据表中的数据计算结果可知, 3次测试下基于改进SVM的互联网用户分类结果, 其分类平均准确率为98.56%, 满足预期, 因此进行下一步对比实验.

2.2 对比测试

实验测试环境和测试条件不变, 分别利用3个模型对浏览新闻的用户进行分类, 对照组1是基于SVM的互联网用户分类模型, 对照组2是文献[3]模型, 实验组为基于改进SVM的互联网用户分类模型, 对比3种模型. 实验结果如图3所示.

根据图中数据可知, 实验组模型的学习样本数量与模型自身提供的样本数量几乎一致. 对照1组模型的学习样本数量, 在模型自身提供的样本数量达到1000时其学习数量迅速下降且难以恢复. 对照2组模型的学习样本数量, 比其自身提供的样本数量少了近1倍. 相比较而言, 此次设计的模型性能更好. 表4为模型性能比较分析结果.

根据表中分析结果可知, 3组模型虽然都是根据用户偏好特征进行分类, 但获取偏好特征的方式不同, 再加之模型自身约束了选择的样本, 导致模型学习性能下降. 可见此次设计的分类模型, 解决了模型学习能力不足的问题.

3 结束语

传统的分类模型与此次设计的分类模型都将用户偏好作为详细分类的依据, 改进的SVM充分发挥其强大的学习能力, 对分类后的样本数据进行学习, 当该模型获取到入网用户信息后, 根据其浏览内容迅速判断用户类型, 提醒软件推送用户感兴趣的各类信息. 此次研究受时间的限制没有介绍SVM的改进内容, 而是直接将改进后的SVM投入使用, 在今后的研究项目将对改进过程、改进内容加以描述.