DCCP作为一种适用于实时多媒体流的传输协议, 拥有UDP不可靠传输特性和TCP的拥塞控制机制的特点, 它作为一种通用的底层协议, 避免了在应用层上进行拥塞控制算法设计与实现. 围绕DCCP的研究包括了提高多媒体流传输的实时性, 优化传输速率稳定性等方面. 关键的优化点围绕DCCP中的AIMD机制展开, 文献[1]基于卡尔曼滤波对CCID2算法[2]进行改进, 但这种算法的复杂度可能给网络资源带来过多的消耗. 文献[3]考虑了误码丢包, 使用信道繁忙比来检测网络拥塞的方法对CCID2进行优化, 适用于特殊的Ad hoc网络, 但是这种优化并没有改变算法AIMD的本质, 无法使算法在获得高吞吐量的同时保持低延迟. 由于丢包作为这类算法的唯一输入信号, 算法的正常运行对链路的丢包率有一定的要求, 在丢包率较高的长肥管道环境下, 其发送窗口会收敛到很小的值[4]. 随着网络中间设备的队列深度扩增, 基于丢包的拥塞控制算法已经不再适合如今的网络环境, 这类算法的拥塞避免阶段会逐渐加大发送窗口直至填满瓶颈队列, 正是这种机制本身导致了链路拥塞, 造成了网络延时的波动. 在链路瓶颈处保持最大带宽和最小延时的状态是拥塞控制的目标, 但这个状态曾被证明不可能由分布式算法收敛[5]. 最近谷歌提出一种基于延时带宽积的算法BBR (Bottleneck Bandwidth and RTT)[6], 使用了交替测试链路的最大带宽与最小的RTT的方法, 通过估计链路BDP的思路解决了这个问题. BBR算法致力于收敛到最佳的拥塞控制点, 因此适合DCCP这种对于延时和带宽敏感的流媒体传输协议, 本文在DCCP中引入BBR算法, 考虑到DCCP与TCP传输模型的差异, 对链路瓶颈带宽的计算方法进行适配, 为了增加算法抵抗丢包的能力, 此外, 本文在BBR的基础上加入动态测量丢包率的机制, 优化BBR在固定增益系数下存在的失速问题. 经过仿真实验验证, 改进后的算法可以在高吞吐量的状态下保持低延时, 提高了在高丢包率的网络环境下连接的吞吐量.
1 CCID2算法模型CCID2是一种类TCP的拥塞控制算法, 并不保证数据可靠性, 它使用AIMD机制计算拥塞窗口限制发送速率以适应不同的网络环境. CCID2应用在DCCP上, 其拥塞窗口的单位与TCP不同, 在TCP上单位为字节, 而在DCCP上单位为数据报数量, 传输的单位为数据包. CCID2使用类似TCP-SACK方法来实现拥塞控制机制, 然而, 作为一种Loss-Base的拥塞控制算法, 它存在以下缺点:
1)带宽利用率低, CCID2本质上属于丢包事件驱动的拥塞控制算法, 当链路的丢包率上升至1%以上的时, 算法基本上无法正常工作.
2)缓冲区膨胀问题(
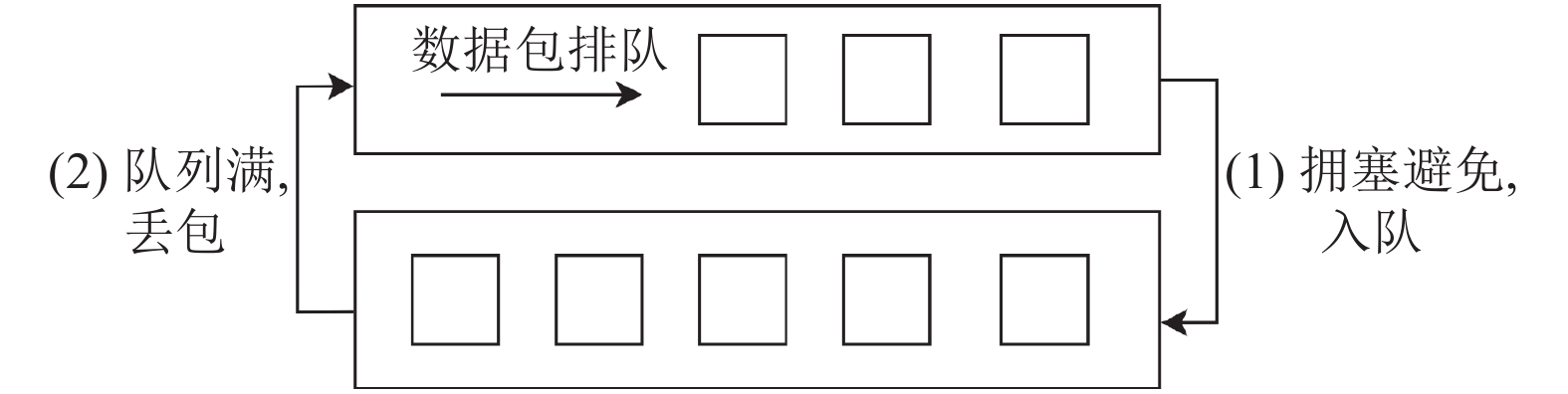
|
图 1 Loss-Base拥塞控制算法事件循环 |
2 BBR算法模型
BBR算法与基于丢包的拥塞控制算法不同, 在BBR算法的模型中, 定义了链路的最大负载为链路的时延RTT与链路带宽的乘积(Bandwidth Delay Product, BDP), 如果发送端往网络注入数据包的速度超过了BDP, 中间设备也无法转发更多的数据包, 后续加入数据包会开始排队导致链路延时开始增加. 在BBR中链路的RTT由(1)式计算:
| $RTProp' = RTProp + \min\left( {{\eta _t}} \right)$ | (1) |
其中, RTProp的值为链路延迟, 由链路物理长度决定, 而
BBR算法模型如图2所示.

|
图 2 BBR算法事件循环 |
算法在(1)阶段会探测链路的最大带宽, 该阶段链路会出现排队的情况, 随后在(2)阶段按同样的比例排空发送过多的数据包, 随后进入稳定的(3)阶段, PROPBW会周期性探测链路的带宽. 在(3-1)的探测阶段内, 算法会少量增加发送数量以探测链路空闲带宽, 随后在(3-2)阶段会按相应的比例降低发送数量, BBR避免了Loss-Base算法一直填满缓冲队列的做法, 因此可以同时保持高带宽利用率和较低的延迟. 实际上, 链路最低延时与最大带宽无法同时测量, 要测量带宽必须往链路发送过量的数据以计算获得最大的实际带宽, 此时由于大量数据包排队, 必然会导致延时的增加. 另一方面, 要测量链路延时, 必须保证连接本身没有对中间设备进行排队, 这时需要减少数据的发送量. BBR使用交替测试RTT与链路带宽的做法解决了上述问题. 尽管如此, BBR仍然存在以下的缺陷:
1) BBR算法在STARTUP过程中, 为了适应不同链路的带宽情况, 使用二分搜索的方法探测链路的BDP, 具体计算过程如下(下面使用G代替PACING_GAIN):
① 定义STARTUP过程的发送速率SendingRate为RTT时间的函数(其中α为常系数):
| $SendingRate(t) = \alpha {2^t}$ | (2) |
② 为得到PACING_GAIN, 令当前时间为t−2, 对于[t−2, t−1]区间有:
| $SendingRate(t - 2) = \alpha {2^{t - 2}}$ | (3) |
③ 由于PACING_GAIN与当前SendingRate的积定义了下一个周期的SendingRate, 从而有:
| $G \times SendingRate(t - 2) = BD{P_{[t - 1,t]}}$ | (4) |
④ 对RTT归一化处理后, 计算出增益系数的值:
| $\left\{ {\begin{array}{l} G \times SendingRate(t - 2) = BD{P_{{\rm{[}}t - 1, t{\rm{]}}}} \\ G = \dfrac{{BD{P_{{\rm{[}}t - 1, t{\rm{]}}}}}}{{SendingRate(t - 2)}} \\ G = \dfrac{{\alpha \displaystyle\int_{t - 1}^t {{2^t}dt} }}{{\alpha {2^{t - 2}}}} \\ G = \dfrac{2}{{{\rm {ln}}2}} \approx 2.89 \end{array}} \right. $ | (5) |
使用该系数可以使探测算法在
2) 文献[16]指出, BBR算法在丢包率过高的环境下并不能一直保持有效的吞吐量, 丢包率主要由PACING_GAIN的正系数保证, 在丢包率波动很大的环境下, 若网络的丢包率超过固定的增益参数可以调整的范围, 会导致发送速率逐步收敛到低值.
3 DCCP-BBR算法模型与实现DCCP-BBR算法引入了带宽, 丢包率和动态增益系数计算的模型.
3.1 带宽计算由于CCID2只记录数据包序号, 没有记录数据包的大小, 为了测量链路的实际带宽, 需要记录发送窗口内的数据包序号及其对应的包大小的状态:
| $Map\left[ {seq \to packet\;si{\textit{z}}e} \right]$ |
对于ACK的计算, 沿用原有的ACK-Ratio机制, 默认值为2, 此外, 算法使用两个事件更新的带宽信息:
1) onSend()事件
该事件发生在每一个数据包进行发送的时刻, 需要记录数据包的元信息用于后续的带宽估计:
① 记录发送的时间:
| $packet{\rm{\_}}send{\rm{\_}}time\left[ {seq} \right]$ |
② 记录发送时刻的送达数据量delivered_size值:
| $packet{\rm{\_}}send{\rm{\_}}delivered\left[ {seq} \right]$ |
③ 记录发送数据包的大小:
| $packet{\rm{\_}}si{\textit{z}}e\left[ {seq} \right]$ |
2) onAck()事件:
该事件在每收到一个ACK时触发, 需要计算带宽与延时的测量值, 计算伪代码如图3所示.

|
图 3 onAck事件伪代码示意图 |
具体的计算流程如下:
① 累计当前数据包的大小至delivered_size中, 该变量记录连接收到ACK确认的总量.
② 计算数据包发送到接受完毕时候所传输的数据量delivered.
③ 计算数据包送达的时间RTT, 对于接收到多个ACK的Vector, 取ACK包发送时间的最小送达所完成的时间RTT.
④ 计算实时带宽的估计值bw.
至此, 结合bw值与PACING_GAIN增益系数的乘积即可导出发送窗口的值.
3.2 丢包率估计连接的丢包率可以在发送端也可以在接收端计算. 考虑延迟ACK的影响, 在发送计算时如果出现接收端ACK丢失的问题, 会导致计算的Loss-Rate偏大. 为了更准确地估计链路的丢包率, 本实现选择在接收端进行丢包率计算, 然后反馈在ACK报文中. 计算流程如下:
1)协议保证每一个数据报序号总是单调递增的.
2)对于每一个接收到的数据包, 判断数据包是否在10 s有效窗口内, 记录在窗口时间内接收到的数据总量W_ALL, 丢包率在全局窗口内计算.
3)若出现乱序到达的情况, 按照规则2)对丢包率进行补偿. 在每一个窗口内, 记录实际收包总量P_NUMS. 最终的丢包率由式(6)计算:
| $Loss-Rate = \frac{{P\_LOSS}}{{W\_ALL}} = 1 - \frac{{P\_NUMS}}{{W\_ALL}}$ | (6) |
BBR算法在绝大多数时间内处于ProbeBW状态, 其主要工作为探测链路是否有未利用的带宽资源, 算法引入了使用了8个阶段的Gain Cycle状态, 分别为1.25, 0.75, 1, 1, 1, 1, 1, 1. 增益系数在上述数组中循环取值, 算法在每一个阶段持续时间约为RTprop. BBR首先使用1.25系数增加发包数量, 如果实际反馈计算的带宽增加, 意味着BBR可以占据链路空余的带宽. 但由于1.25增益阶段可能导致的链路瓶颈队列排队, 算法设置了0.75增益阶段用于排空瓶颈队列. 随后, 算法的平稳阶段采用1作为增益参数, 按照反馈带宽进行发包, 以此保证连接的公平性. BBR增益系数轮转机制的参数确定主要源于以下几个方面的考虑:
1)平稳阶段的长度决定了BBR探测带宽的间隔, 短的间隔提升了探测过程的抢占速度, 长的间隔用于保证公平性, 两者并不能同时兼顾.
2)较大的增益系数可以增加算法竞争性, 在链路有空闲资源的时候可以更快收敛到新的BDP, 但也会对链路延迟产生较大的波动.
3)较小的增益系数一定程度上减少了竞争性, 同时也意味着每一个ProbeBW阶段的收益会降低, 收敛到新BDP需要更长的时间.
如果增益系数过小, 正增益的效果会完全被丢包副作用抵消, 从而导致发送速率持续下降. 由于BBR算法增益系数是固定的, 1.25增益系数只能保证在20%丢包率以下工作, DCCP-BBR采用动态计算增益系数的方法. 引入丢包率(Loss-Rate)参数, 使用丢包率导出实时的增益系数, 对于每一个反馈的Loss-Rate, 发送端在每一个新的ProbeBW周期, 需要调整PACING_GAIN系数. 具体调整公式如下:
对于估算的BTLBW值, 其增益系数需要满足式(7)(下面使用BW代替BTLBW):
| $PACING\_GAIN \times BW \ge BW$ | (7) |
上式保证正增益后的值大于当前的瓶颈带宽, 否则最大BW的估计值会不断地出现负反馈的情况, 引入丢包率后, 需要保证:
| $\begin{split} & PACING\_GAIN \times BW \times \left( {1 - LossRate} \right) \ge BW \\ & PACING\_GAIN \ge \frac{1}{{\left( {1 - LossRate} \right)}} \end{split} $ | (8) |
考虑到PACING_GAIN过大会对链路造成压力, 取1.5为上限值, 最终的系数计算如下(其中LR为丢包率):
| $\begin{split} &{{PACING\_GAIN = }}\\ &\left\{{\begin{array}{*{20}{c}} {{\rm{1}}{\rm{.25}}}&{{\rm{0}}{\rm{.75}}}&{\rm{1}}&{{\rm{1}}\cdots}&{}&{{{LR < = 0}}{\rm{.2}}} \\ {{\rm{1}}{\rm{.50}}}&{{\rm{0}}{\rm{.50}}}&{\rm{1}}&{{\rm{1}}\cdots}&{}&{{{LR > 0}}{\rm{.3}}} \\ {\dfrac{{\rm{1}}}{{{{1 - LR}}}}}&{\dfrac{{{\rm{1 - 2}} \times {{LR}}}}{{{{1 - LR}}}}}&{\rm{1}}&{{\rm{1}}\cdots}&{}&{{\rm{0}}{{.2 < LR < = 0}}{\rm{.3}}} \end{array}} \right. \end{split}$ | (9) |
算法使用了Hashmap跟踪发送窗口数据包状态, 对于发送方, RTT与BW的计算需要获取对应数据包的发送的时间packet_send_time, 发送时刻的已送达数据量delivered_size与数据包的大小packet_size, 三者可共享一个哈希表, 每一条记录需要约20字节, 计算过程可在O(1)时间完成. 哈希表所需空间为发送窗口/数据包大小(发送窗口上限为链路BDP). 对数据包按MTU大小估计, 记录所需的空间约为:
| $20 \times \frac{{{{BDP}}}}{{{{MTU}}}}$ | (10) |
由于接收方不需要维护数据包的元信息(meta data), 只需要保留10 s窗口的历史记录, 如图4所示.
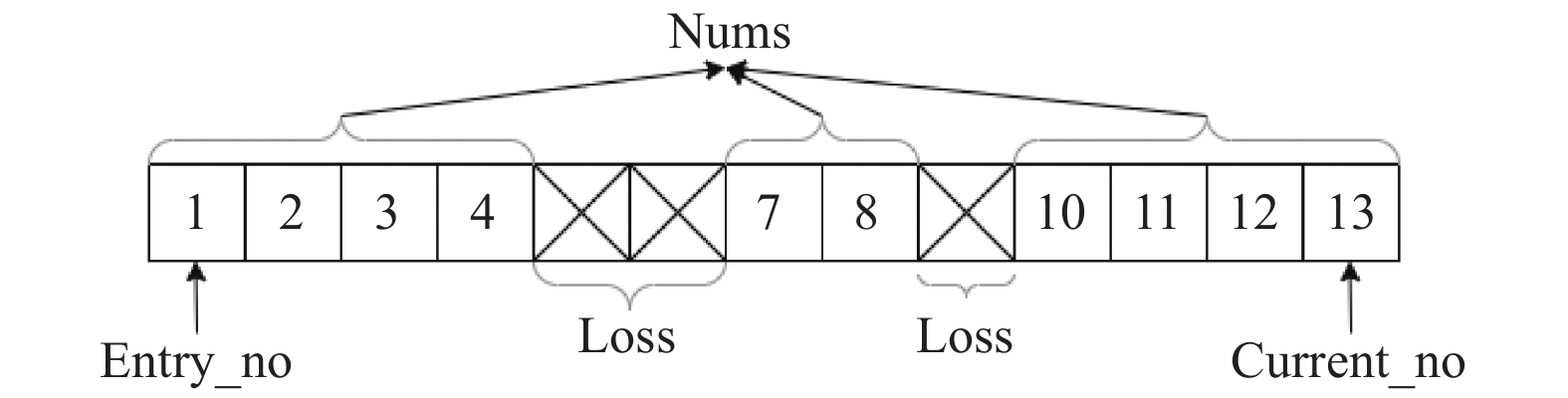
|
图 4 丢包率计算示意图 |
窗口内需要标记入口序列号entry_no, 当前序列号current_no与窗口内接收到数据包的数量nums. 并根据下式导出窗口内的丢包率:
| $LossRate = 1 - \frac{{nums}}{{current\_no - entry\_no}}$ | (11) |
丢包率反馈过程计算复杂度为O(1), 不需要额外空间.
4 仿真模拟实验为了验证基于BBR改进后的DCCP协议的性能, 本实验使用网络模拟器MININET[17]模拟网络环境. 在两台主机上面进行带宽测试, 在不同丢包率环境下(0~0.4), 分别与CCID2, 原BBR算法的实现进行对比. 测试环境的网络拓扑如图5所示.

|
图 5 仿真实验网络拓扑 |
图5中路由器r1与r2之间为测试的瓶颈链路, s1–s3为发送端, d1–d3为接收端, 所有发送端与r1连接, 接收端与r2连接. 瓶颈链路的带宽设置为100 Mb/s, 其余所有链路的带宽均为1 GB/s, 路由器与客户端连接不附加往返延迟, 路由器r1与r2之间l2的往返延迟设置为100 ms, 路由队列长度max_queue_size设置为4 k, 队列控制算法使用Drop-Tail.
4.1 DCCP-BBR与CCID2负载时链路延时测试为了给链路加上负载, 使用s2–s3两个发送端分别向d2–d3建立TCP连接, 并且使用Vegas算法进行不限速数据发送, 目的是将路由器r1–r2之间的负载填充至瓶颈值, 但保持路由器缓冲区的空闲. 随后在s1分别使用DCCP-BBR, DCCP-CCID2与d1进行链路延时的测试.
图6描述了两种算法在传输时间为15 s窗口内的网络延时, 显示了从连接启动到平稳状态时候的性能. 其中使用CCID2的连接进入后迅速增大了链路的延迟, 进入平稳状态后达到高吞吐量后无法维持低RTT, 这是因为CCID2会一直耗尽链路的缓冲队列直到出现Drop-Tail丢包. BBR-DCCP则获得比较均衡的结果, 表现出较低的侵略性, 仅在STARTUP阶段探测链路最大带宽的时候主动往缓冲队列排队, 导致链路的延时暂时的上升, 当其检测到增大发送速率不再增加有效带宽的时候即退出启动阶段, 随后进入的平稳阶段会周期性地探测带宽, 导致链路延时小幅度波动, 总体上, 在保证高吞吐量的同时仍可以维持低的链路RTT, 平均链路延时相比CCID2降低了20%.

|
图 6 延时对比测试结果 |
4.2 DCCP-BBR与BBR在不同丢包率下的吞吐量测试
本单元测试单连接的吞吐量, 使用同样的网络拓扑结构, 使用s1发送端与d1进行连接, 剩余节点均为关闭状态, 其他链路参数保持不变. 对l2链路设定不同的丢包率分别进行测试.
图7描述了3种算法独立在网络中进行数据传输时, 吞吐量随丢包率变化的表现. 横坐标为链路丢包率, 由0逐渐增大至0.4. 纵坐标为连接在对应丢包率下的平均吞吐量. 对于CCID2算法, 在丢包率高于1%的时候就处于不可用状态, 原因为丢包对算法的窗口计算造成持续的负反馈, 每一次丢包窗口将减少一半, 一直收敛到接近于0. 另一方面, BBR在丢包率高于20%的时候其增益系数无法平衡掉高丢包率带来的副作用, 出现吞吐量急剧下降. 改进后的BBR-DCCP由于其增益参数由实时丢包率计算导出, 动态调整为与链路拥塞状态匹配的值, 避免了持续的负系数反馈. 与BBR相比, BBR-DCCP抵抗丢包的能力提高了10%.

|
图 7 不同丢包率下吞吐量测试结果 |
5 结论
针对传统拥塞控制算法CCID2存在缓冲区膨胀的问题, 本文提出了基于BBR改进的数据报拥塞控制协议算法, 在原有BBR算法基础上增加了丢包率估计模型, 解决了在高丢包率的网络环境下连接失速的问题. 实验结果表明, 本算法可以在高带宽利用率的同时保持相对较低的延迟, 此外, 通过丢包率模型动态地调整增益系数, 算法在丢包率较高的环境下也能保持良好的吞吐量.
| [1] |
黄玉清. 基于DCCP的多媒体流实时控制算法研究[硕士学位论文]. 武汉: 华中师范大学, 2017.
|
| [2] |
Floyd S, Kohler E. Profile for DCCP Congestion Control ID 2: TCP-like Congestion Control. 2002.
|
| [3] |
卢先领, 施利利. WSN中一种改进的DCCP拥塞控制机制. 计算机应用与软件, 2015, 32(6): 136-139. DOI:10.3969/j.issn.1000-386x.2015.06.033 |
| [4] |
Polese M, Chiariotti F, Bonetto E, et al. A survey on recent advances in transport layer protocols. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3584-3608. |
| [5] |
Jaffe J. Flow control power is nondecentralizable. IEEE Transactions on Communications, 1981, 29(9): 1301-1306. DOI:10.1109/TCOM.1981.1095152 |
| [6] |
Cardwell N, Cheng YC, Gunn CS, et al. BBR: Congestion-based congestion control: Measuring bottleneck bandwidth and round-trip propagation time. Queue, 2016, 14(5): 20-53. DOI:10.1145/3012426.3022184 |
| [7] |
Cerf VG. Bufferbloat and other Internet challenges. IEEE Internet Computing, 2014, 18(5): 80. DOI:10.1109/MIC.2014.89 |
| [8] |
Gettys J, Nichols K. Bufferbloat: Dark buffers in the Internet. Communications of the ACM, 2012, 55(1): 57-65. DOI:10.1145/2063176.2063196 |
| [9] |
Chowdhury T, Alam M. Performance evaluation of TCP Vegas over TCP Reno and TCP NewReno over TCP Reno. JOIV: International Journal on Informatics Visualization, 2019, 3(3): 275-282. |
| [10] |
Guo YJ, Yang XP, Wang R, et al. TCP adaptive Vegas: Improving of TCP vegas algorithm. Proceedings of 2014 International Conference on Information Science, Electronics and Electrical Engineering. Sapporo, Japan. 2014.126–130.
|
| [11] |
Jin C, Wei DX, Low SH. FAST TCP: Motivation, architecture, algorithms, performance. Proceedings of IEEE INFOCOM 2004. Hong Kong, China. 2004. 2490–2501.
|
| [12] |
Adams R. Active queue management: A survey. IEEE Communications Surveys & Tutorials, 2013, 15(3): 1425-1476. |
| [13] |
Ismail AH, Elsagheer Z, Morsi IZ. Survey on random early detection mechanism and its variants. IOSR Journal of Computer Engineering, 2012, 2(6): 20-24. |
| [14] |
Sivov A, Sokolov VA. The bufferbloat problem and TCP: Fighting with congestion and latency. Proceedings of the Spring/Summer Young Researchers’ Colloquium on Software Engineering. 2012.
|
| [15] |
Hurtig P, Haile H, Grinnemo KJ, et al. Impact of TCP BBR on CUBIC traffic: A mixed workload evaluation. Proceedings of the 2018 30th International Teletraffic Congress. Vienna, Austria. 2018. 218–226.
|
| [16] |
Cao Y, Jain A, Sharma K, et al. When to use and when not to use BBR: An empirical analysis and evaluation study. Proceedings of Internet Measurement Conference. Amsterdam, the Netherlands. 2019. 130–136.
|
| [17] |
Xiang Z, Seeling P. Mininet: An Instant Virtual Network on Your Computer. In: Fitzek FHP, Granelli F, Seeling P, eds. Computing in Communication Networks. New York: Academic Press, 2020. 219–230.
|
 2021, Vol. 30
2021, Vol. 30



